Eureka Math

Engage NY Eureka Math 8th Grade Module 4 Lesson 25 Answer Key

Eureka Math Grade 8 Module 4 Lesson 25 Exercise Answer Key

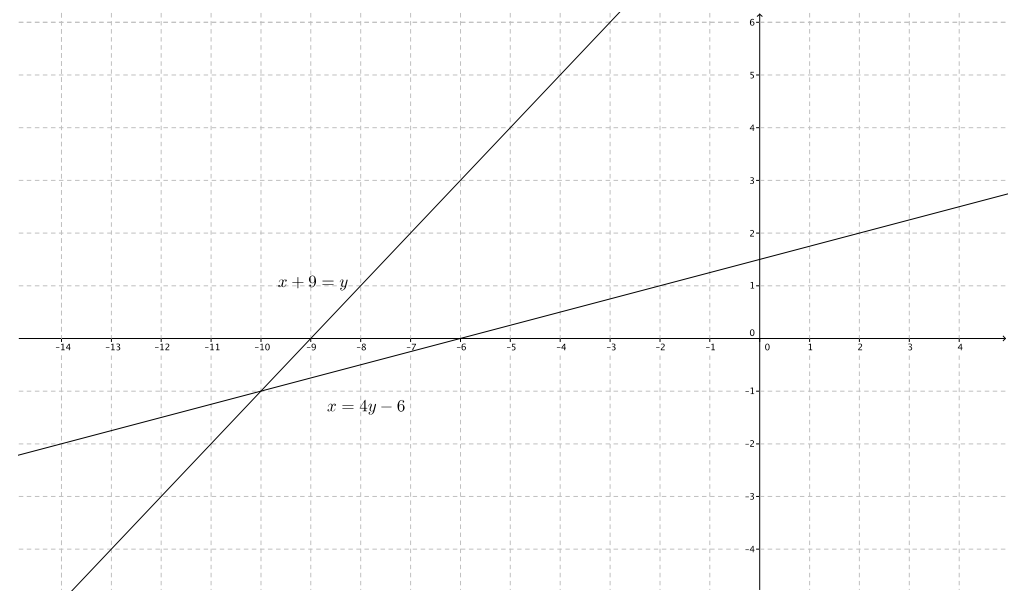
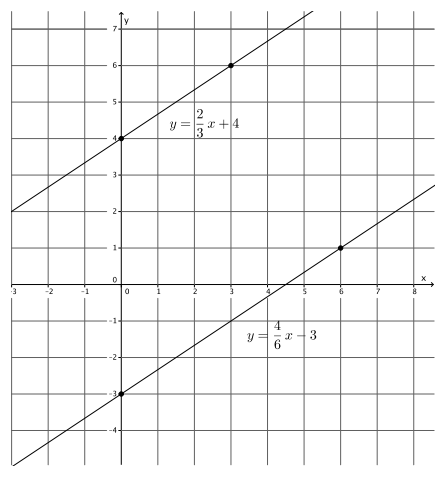
Exploratory Challenge/Exercises 1–5

Exercise 1.
Sketch the graphs of the linear system on a coordinate plane: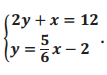

Answer:
For the equation 2y + x = 12:
2y + 0 = 12
2y = 12
y = 6
The y – intercept point is (0, 6).
2(0) + x = 12
x = 12
The x – intercept point is (12, 0).
For the equation y = \(\frac{5}{6}\) x – 2:
The slope is \(\frac{5}{6}\), and the y – intercept point is (0, – 2).

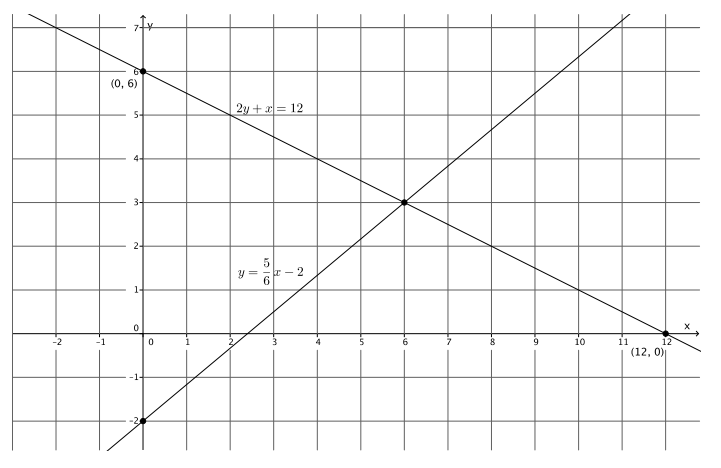
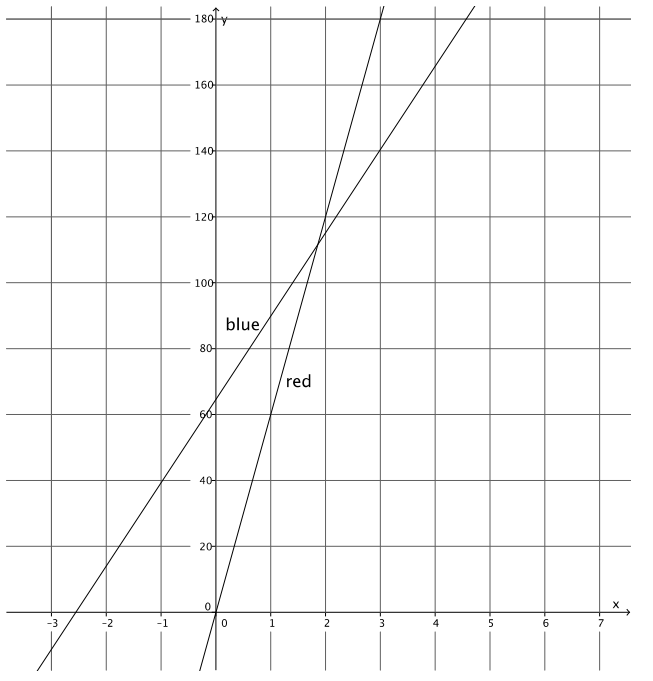
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
(6, 3)

b. Verify that the ordered pair named in part (a) is a solution to 2y + x = 12.
Answer:
2(3) + 6 = 12
6 + 6 = 12
12 = 12
The left and right sides of the equation are equal.

c. Verify that the ordered pair named in part (a) is a solution to y = \(\frac{5}{6}\) x – 2.
Answer:
3 = \(\frac{5}{6}\) (6) – 2
3 = 5 – 2
3 = 3
The left and right sides of the equation are equal.

d. Could the point (4, 4) be a solution to the system of linear equations? That is, would (4, 4) make both equations true? Why or why not?
Answer:
No. The graphs of the equations represent all of the possible solutions to the given equations. The point (4, 4) is a solution to the equation 2y + x = 12 because it is on the graph of that equation. However, the point (4, 4) is not on the graph of the equation y = \(\frac{5}{6}\) x – 2. Therefore, (4, 4) cannot be a solution to the system of equations.

Exercise 2.
Sketch the graphs of the linear system on a coordinate plane:
x + y = – 2
y = 4x + 3

Answer:
For the equation x + y = – 2:
0 + y = – 2
y = – 2
The y – intercept point is (0, – 2).
x + 0 = – 2
x = – 2
The x – intercept point is ( – 2, 0).
For the equation y = 4x + 3:
The slope is \(\frac{4}{1}\), and the y – intercept point is (0, 3).

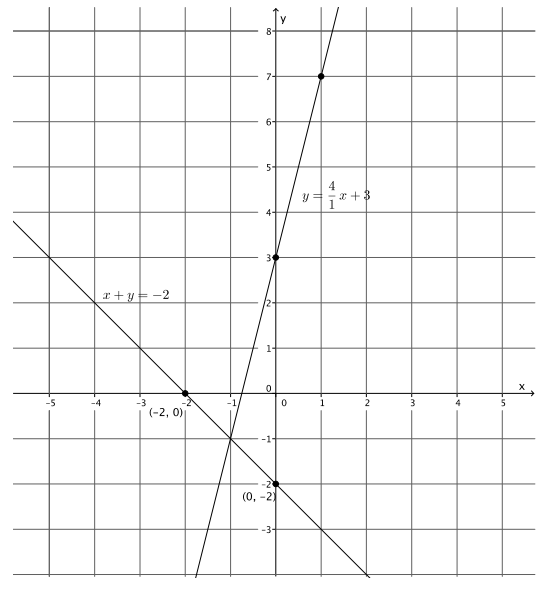
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
( – 1, – 1)

b. Verify that the ordered pair named in part (a) is a solution to x + y = – 2.
Answer:
– 1 + ( – 1) = – 2
– 2 = – 2
The left and right sides of the equation are equal.

c. Verify that the ordered pair named in part (a) is a solution to y = 4x + 3.
Answer:
– 1 = 4( – 1) + 3
– 1 = – 4 + 3
– 1 = – 1
The left and right sides of the equation are equal.

d. Could the point ( – 4, 2) be a solution to the system of linear equations? That is, would ( – 4, 2) make both equations true? Why or why not?
Answer:
No. The graphs of the equations represent all of the possible solutions to the given equations. The point ( – 4, 2) is a solution to the equation x + y = – 2 because it is on the graph of that equation. However, the point ( – 4, 2) is not on the graph of the equation y = 4x + 3. Therefore, ( – 4, 2) cannot be a solution to the system of equations.

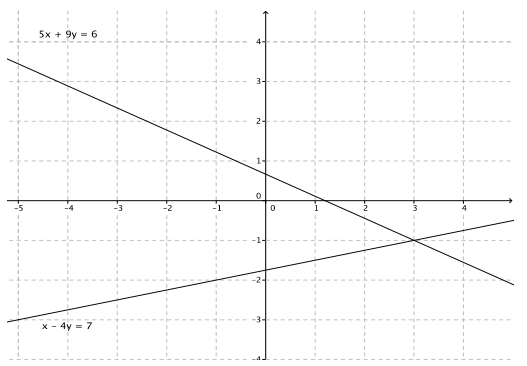
Exercise 3.
Sketch the graphs of the linear system on a coordinate plane:
3x + y = – 3
– 2x + y = 2

Answer:
For the equation 3x + y = – 3:
3(0) + y = – 3
y = – 3
The y – intercept point is (0, – 3).
3x + 0 = – 3
3x = – 3
x = – 1
The x – intercept point is ( – 1, 0).
For the equation – 2x + y = 2:
– 2(0) + y = 2
y = 2
The y – intercept point is (0, 2).
– 2x + 0 = 2
– 2x = 2
x = – 1
The x – intercept point is ( – 1, 0).

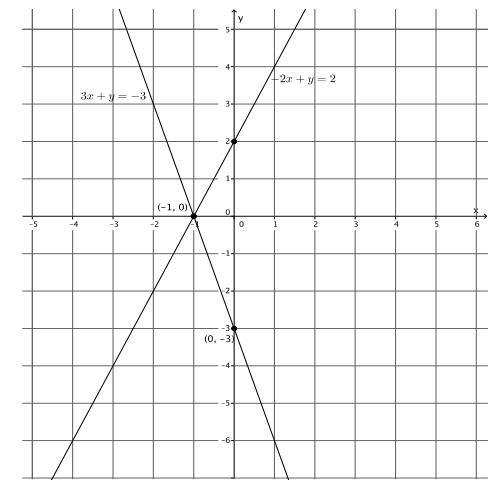
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
( – 1, 0)

b. Verify that the ordered pair named in part (a) is a solution to 3x + y = – 3.
Answer:
3( – 1) + 0 = – 3
– 3 = – 3
The left and right sides of the equation are equal.

c. Verify that the ordered pair named in part (a) is a solution to – 2x + y = 2.
Answer:
– 2( – 1) + 0 = 2
2 = 2
The left and right sides of the equation are equal.

d. Could the point (1, 4) be a solution to the system of linear equations? That is, would (1, 4) make both equations true? Why or why not?
Answer:
No. The graphs of the equations represent all of the possible solutions to the given equations. The point (1, 4) is a solution to the equation – 2x + y = 2 because it is on the graph of that equation. However, the point (1, 4) is not on the graph of the equation 3x + y = – 3. Therefore, (1, 4) cannot be a solution to the system of equations.

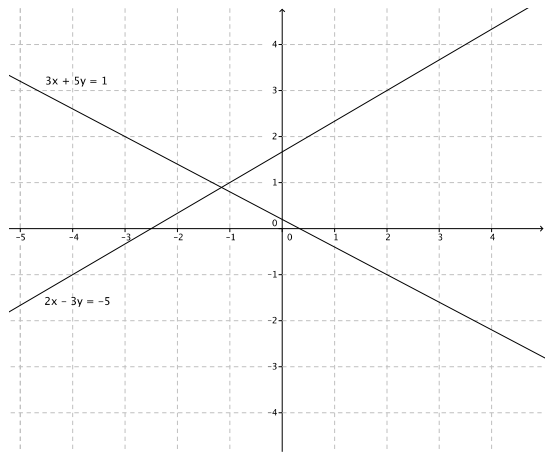
Exercise 4.
Sketch the graphs of the linear system on a coordinate plane:
2x – 3y = 18
2x + y = 2

Answer:
For the equation 2x – 3y = 18:
2(0) – 3y = 18
– 3y = 18
y = – 6
The y – intercept point is (0, – 6).
2x – 3(0) = 18
2x = 18
x = 9
The x – intercept point is (9, 0).
For the equation 2x + y = 2:
2(0) + y = 2
y = 2
The y – intercept point is (0, 2).
2x + 0 = 2
2x = 2
x = 1
The x – intercept point is (1, 0).

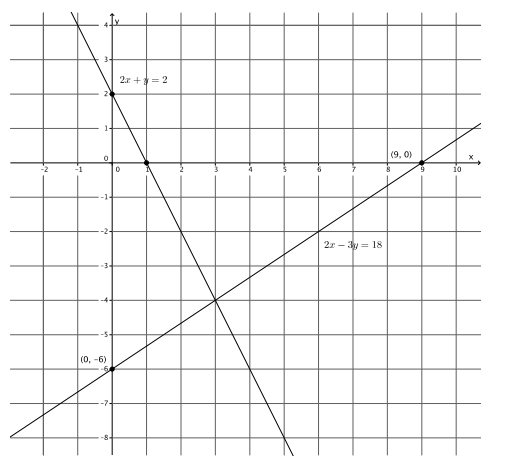
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
(3, – 4)

b. Verify that the ordered pair named in part (a) is a solution to 2x – 3y = 18.
Answer:
2(3) – 3( – 4) = 18
6 + 12 = 18
18 = 18
The left and right sides of the equation are equal.

c. Verify that the ordered pair named in part (a) is a solution to 2x + y = 2.
Answer:
2(3) + ( – 4) = 2
6 – 4 = 2
2 = 2
The left and right sides of the equation are equal.

d. Could the point (3, – 1) be a solution to the system of linear equations? That is, would (3, – 1) make both equations true? Why or why not?
Answer:
No. The graphs of the equations represent all of the possible solutions to the given equations. The point (3, – 1) is not on the graph of either line; therefore, it is not a solution to the system of linear equations.

Exercise 5.
Sketch the graphs of the linear system on a coordinate plane:
y – x = 3
y = – 4x – 2

Answer:
For the equation y – x = 3:
y – 0 = 3
y = 3
The y – intercept point is (0, 3).
0 – x = 3
– x = 3
x = – 3
The x – intercept point is ( – 3, 0).
For the equation y = – 4x – 2:
The slope is – \(\frac{4}{1}\), and the y – intercept point is (0, – 2).

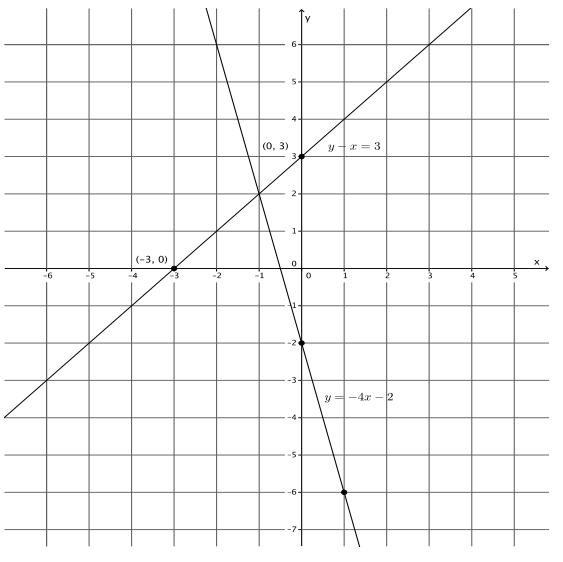
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
( – 1, 2)

b. Verify that the ordered pair named in part (a) is a solution to y – x = 3.
Answer:
2 – ( – 1) = 3
3 = 3
The left and right sides of the equation are equal.

c. Verify that the ordered pair named in part (a) is a solution to y = – 4x – 2.
Answer:
2 = – 4( – 1) – 2
2 = 4 – 2
2 = 2
The left and right sides of the equation are equal.

d. Could the point ( – 2, 6) be a solution to the system of linear equations? That is, would ( – 2, 6) make both equations true? Why or why not?
Answer:
No. The graphs of the equations represent all of the possible solutions to the given equations. The point ( – 2, 6) is a solution to the equation y = – 4x – 2 because it is on the graph of that equation. However, the point ( – 2, 6) is not on the graph of the equation y – x = 3. Therefore, ( – 2, 6) cannot be a solution to the system of equations.

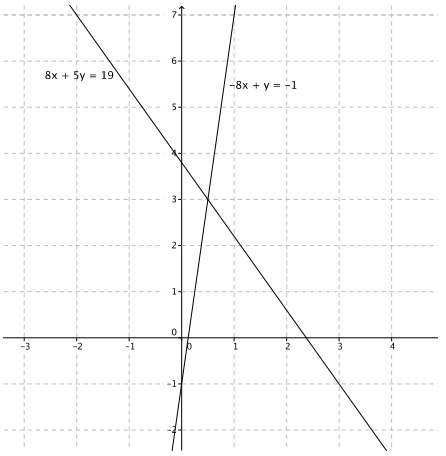
Exercise 6.
Write two different systems of equations with (1, – 2) as the solution.
Answer:
Answers will vary. Two sample solutions are provided:

Eureka Math Grade 8 Module 4 Lesson 25 Problem Set Answer Key

Question 1.
Sketch the graphs of the linear system on a coordinate plane:
y = \(\frac{1}{3}\) x + 1
y = – 3x + 11
Answer:
For the equation y = \(\frac{1}{3}\) x + 1:
The slope is \(\frac{1}{3}\), and the y – intercept point is (0, 1).
For the equation y = – 3x + 11:
The slope is – \(\frac{3}{1}\), and the y – intercept point is (0, 11).

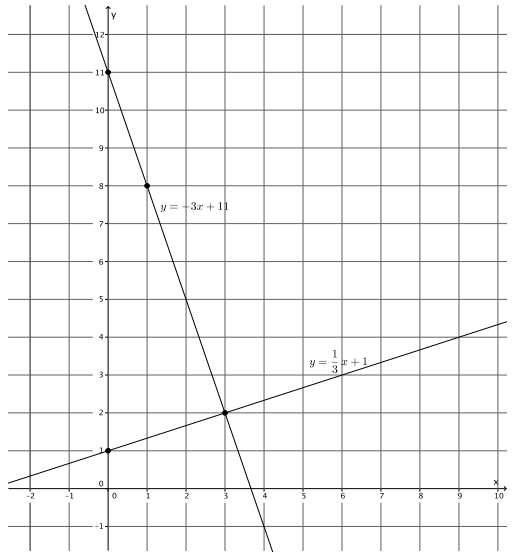
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
(3, 2)

b. Verify that the ordered pair named in part (a) is a solution to y = \(\frac{3}{1}\) x + 1.
Answer:
2 = \(\frac{3}{1}\) (3) + 1
2 = 1 + 1
2 = 2
The left and right sides of the equation are equal.

c. Verify that the ordered pair named in part (a) is a solution to y = – 3x + 11.
Answer:
2 = – 3(3) + 11
2 = – 9 + 11
2 = 2
The left and right sides of the equation are equal.

Question 2.
Sketch the graphs of the linear system on a coordinate plane:
y = \(\frac{1}{2}\) x + 4
x + 4y = 4
Answer:
For the equation y = \(\frac{1}{2}\) x + 4:
The slope is \(\frac{1}{2}\), and the y – intercept point is(0, 4).
For the equation x + 4y = 4:
0 + 4y = 4
4y = 4
y = 1
The y – intercept point is (0, 1).
x + 4(0) = 4
x = 4
The x – intercept point is (4, 0).

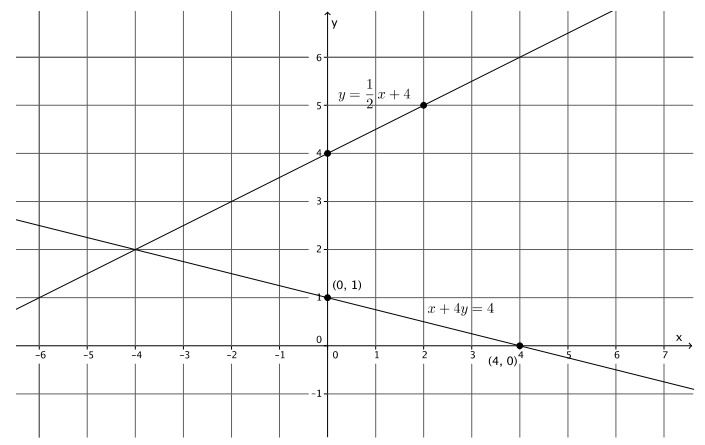
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
( – 4, 2)

b. Verify that the ordered pair named in part (a) is a solution to y = \(\frac{1}{2}\) x + 4.
Answer:
2 = \(\frac{1}{2}\) ( – 4) + 4
2 = – 2 + 4
2 = 2
The left and right sides of the equation are equal.

c. Verify that the ordered pair named in part (a) is a solution to x + 4y = 4.
Answer:
– 4 + 4(2) = 4
– 4 + 8 = 4
4 = 4
The left and right sides of the equation are equal.

Question 3.
Sketch the graphs of the linear system on a coordinate plane:
y = 2
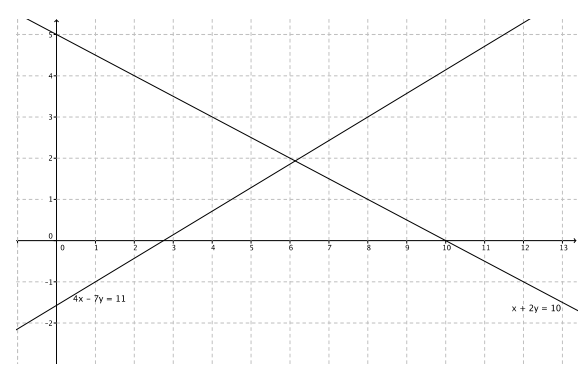
x + 2y = 10
Answer:
For the equation x + 2y = 10:
0 + 2y = 10
2y = 10
y = 5
The y – intercept point is (0, 5).
x + 2(0) = 10
x = 10
The x – intercept point is (10, 0).

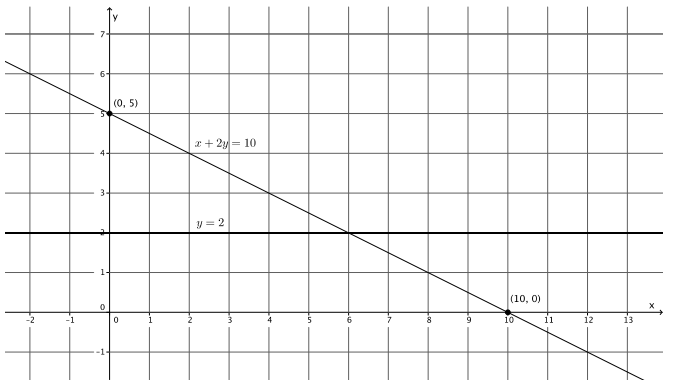
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
(6, 2)

b. Verify that the ordered pair named in part (a) is a solution to y = 2.
Answer:
2 = 2
The left and right sides of the equation are equal.

c. Verify that the ordered pair named in part (a) is a solution to x + 2y = 10.
Answer:
6 + 2(2) = 10
6 + 4 = 10
10 = 10
The left and right sides of the equation are equal.

Question 4.
Sketch the graphs of the linear system on a coordinate plane:
– 2x + 3y = 18
2x + 3y = 6
Answer:
For the equation – 2x + 3y = 18:
– 2(0) + 3y = 18
3y = 18
y = 6
The y – intercept point is (0, 6).
– 2x + 3(0) = 18
– 2x = 18
x = – 9
The x – intercept point is ( – 9, 0).

For the equation 2x + 3y = 6:
2(0) + 3y = 6
3y = 6
y = 2
The y – intercept point is (0, 2).
2x + 3(0) = 6
2x = 6
x = 3
The x – intercept point is (3, 0).

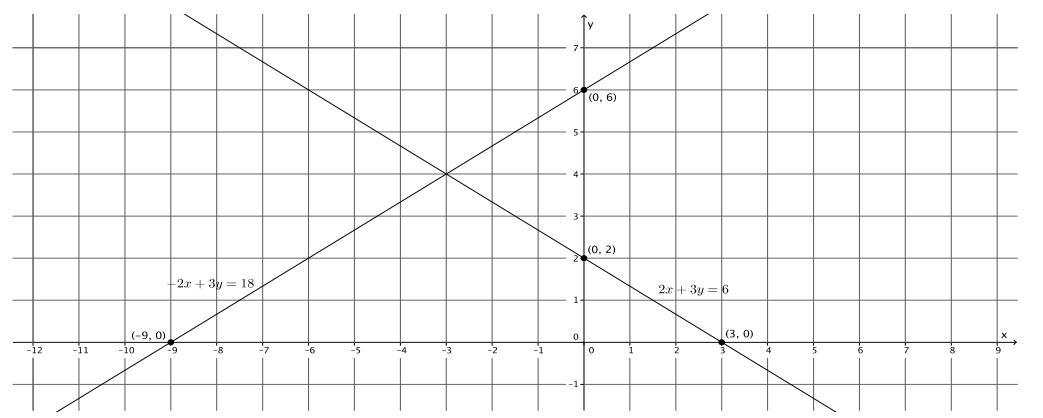
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
( – 3, 4)

b. Verify that the ordered pair named in part (a) is a solution to – 2x + 3y = 18.
Answer:
– 2( – 3) + 3(4) = 18
6 + 12 = 18
18 = 18
The left and right sides of the equation are equal.

c. Verify that the ordered pair named in part (a) is a solution to 2x + 3y = 6.
Answer:
2( – 3) + 3(4) = 6
– 6 + 12 = 6
6 = 6
The left and right sides of the equation are equal.

Question 5.
Sketch the graphs of the linear system on a coordinate plane:
x + 2y = 2
y = \(\frac{2}{3}\) x – 6
Answer:
For the equation x + 2y = 2:
0 + 2y = 2
2y = 2
y = 1
The y – intercept point is (0, 1).
x + 2(0) = 2
x = 2
The x – intercept point is (2, 0).
For the equation y = \(\frac{2}{3}\) x – 6:
The slope is \(\frac{2}{3}\), and the y – intercept point is (0, – 6).

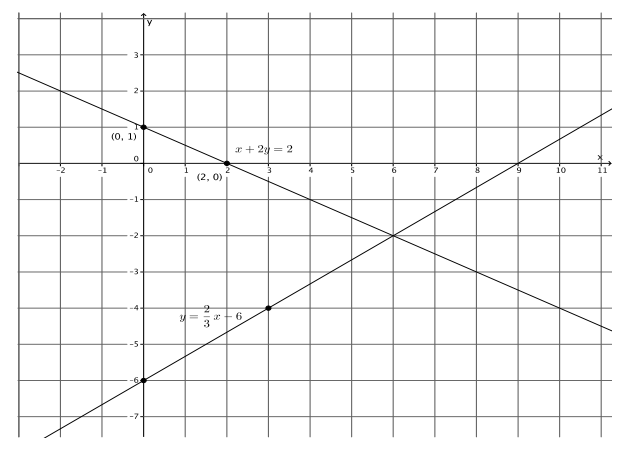
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
(6, – 2)

b. Verify that the ordered pair named in part (a) is a solution to x + 2y = 2.
Answer:
6 + 2( – 2) = 2
6 – 4 = 2
2 = 2
The left and right sides of the equation are equal.

c. Verify that the ordered pair named in part (a) is a solution to y = \(\frac{2}{3}\) x – 6.
Answer:
– 2 = \(\frac{2}{3}\) (6) – 6
– 2 = 4 – 6
– 2 = – 2
The left and right sides of the equation are equal.

Question 6.
Without sketching the graph, name the ordered pair where the graphs of the two linear equations intersect.
x = 2
y = – 3
Answer:
(2, – 3)

Eureka Math Grade 8 Module 4 Lesson 25 Exit Ticket Answer Key

Question 1.
Sketch the graphs of the linear system on a coordinate plane:
2x – y = – 1
y = 5x – 5

Answer:

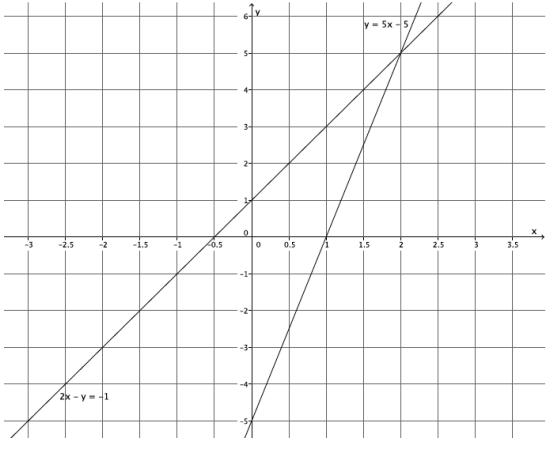
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
(2, 5)

b. Verify that the ordered pair named in part (a) is a solution to 2x – y = – 1.
Answer:
2(2) – 5 = – 1
4 – 5 = – 1
– 1 = – 1
The left and right sides of the equation are equal.

c. Verify that the ordered pair named in part (a) is a solution to y = 5x – 5.
Answer:
5 = 5(2) – 5
5 = 10 – 5
5 = 5
The left and right sides of the equation are equal.

Engage NY Eureka Math 8th Grade Module 4 Lesson 24 Answer Key

Eureka Math Grade 8 Module 4 Lesson 24 Exercise Answer Key

Exercises

Exercise 1.
Derek scored 30 points in the basketball game he played, and not once did he go to the free throw line. That means that Derek scored two-point shots and three-point shots. List as many combinations of two- and three-pointers as you can that would total 30 points.

Answer:

Write an equation to describe the data.
Answer:
Let x represent the number of 2-pointers and y represent the number of 3-pointers.
30 = 2x + 3y

Exercise 2.
Derek tells you that the number of two-point shots that he made is five more than the number of three-point shots. How many combinations can you come up with that fit this scenario? (Don’t worry about the total number of points.)

Answer:

Write an equation to describe the data.
Answer:
Let x represent the number of two-pointers and y represent the number of three-pointers.
x = 5 + y

Exercise 3.
Which pair of numbers from your table in Exercise 2 would show Derek’s actual score of 30 points?
Answer:
The pair 9 and 4 would show Derek’s actual score of 30 points.

Exercise 4.
Efrain and Fernie are on a road trip. Each of them drives at a constant speed. Efrain is a safe driver and travels 45 miles per hour for the entire trip. Fernie is not such a safe driver. He drives 70 miles per hour throughout the trip. Fernie and Efrain left from the same location, but Efrain left at 8:00 a.m., and Fernie left at 11:00 a.m. Assuming they take the same route, will Fernie ever catch up to Efrain? If so, approximately when?
a. Write the linear equation that represents Efrain’s constant speed. Make sure to include in your equation the extra time that Efrain was able to travel.
Answer:
Efrain’s rate is \(\frac{45}{1}\) miles per hour, which is the same as 45 miles per hour. If he drives y miles in x hours at that constant rate, then y = 45x. To account for his additional 3 hours of driving time that Efrain gets, we write the equation y = 45(x + 3).
y = 45x + 135

b. Write the linear equation that represents Fernie’s constant speed.
Answer:
Fernie’s rate is \(\frac{70}{1}\) miles per hour, which is the same as 70 miles per hour. If he drives y miles in x hours at that constant rate, then y = 70x.

c. Write the system of linear equations that represents this situation.
Answer:
y = 45x + 135
y = 70x

d. Sketch the graphs of the two linear equations.

Answer:

e. Will Fernie ever catch up to Efrain? If so, approximately when?
Answer:
Yes, Fernie will catch up to Efrain after about 4 \(\frac{1}{2}\) hours of driving or after traveling about 325 miles.

f. At approximately what point do the graphs of the lines intersect?
Answer:
The lines intersect at approximately (4.5, 325).

Exercise 5.
Jessica and Karl run at constant speeds. Jessica can run 3 miles in 24 minutes. Karl can run 2 miles in 14 minutes. They decide to race each other. As soon as the race begins, Karl trips and takes 2 minutes to recover.
a. Write the linear equation that represents Jessica’s constant speed. Make sure to include in your equation the extra time that Jessica was able to run.
Answer:
Jessica’s rate is \(\frac{3}{24}\) miles per minute, which is equivalent to \(\frac{1}{8}\) miles per minute. If Jessica runs y miles x minutes at that constant speed, then y = \(\frac{1}{8}\) x. To account for her additional 2 minute of running that Jessica gets, we write the equation
y = \(\frac{1}{8}\) (x + 2)
y = \(\frac{1}{8}\) x + \(\frac{1}{4}\)

b. Write the linear equation that represents Karl’s constant speed.
Answer:
Karl’s rate is \(\frac{2}{14}\) miles per minute, which is the same as \(\frac{1}{7}\) miles per minute. If Karl runs y miles in x minutes at that constant speed, then y = \(\frac{1}{7}\) x.

c. Write the system of linear equations that represents this situation.
Answer:
y = \(\frac{1}{8}\) x + \(\frac{1}{8}\)
y = \(\frac{1}{7}\) x

d. Sketch the graphs of the two linear equations.

Answer:

e. Use the graph to answer the questions below.
i. If Jessica and Karl raced for 3 miles, who would win? Explain.
Answer:
If the race were 3 miles, then Karl would win. It only takes Karl 21 minutes to run 3 miles, but it takes Jessica 24 minutes to run the distance of 3 miles.

ii. At approximately what point would Jessica and Karl be tied? Explain.
Answer:
Jessica and Karl would be tied after about 4 minutes or a distance of 1 mile. That is where the graphs of the lines intersect.

Eureka Math Grade 8 Module 4 Lesson 24 Problem Set Answer Key

Question 1.
Jeremy and Gerardo run at constant speeds. Jeremy can run 1 mile in 8 minutes, and Gerardo can run 3 miles in 33 minutes. Jeremy started running 10 minutes after Gerardo. Assuming they run the same path, when will Jeremy catch up to Gerardo?
a. Write the linear equation that represents Jeremy’s constant speed.
Answer:
Jeremy’s rate is \(\frac{1}{8}\) miles per minute. If he runs y miles in x minutes, then y = \(\frac{1}{8}\) x.

b. Write the linear equation that represents Gerardo’s constant speed. Make sure to include in your equation the extra time that Gerardo was able to run.
Answer:
Gerardo’s rate is \(\frac{3}{33}\) miles per minute, which is the same as \(\frac{1}{11}\) miles per minute. If he runs y miles in x minutes, then y = \(\frac{1}{11}\) x. To account for the extra time that Gerardo gets to run, we write the equation
y = \(\frac{1}{11}\) (x + 10)
y = \(\frac{1}{11}\) x + \(\frac{10}{11}\)

c. Write the system of linear equations that represents this situation.
Answer:
y = \(\frac{1}{8}\) x
y = \(\frac{1}{11}\) x + \(\frac{10}{11}\)

d. Sketch the graphs of the two equations.

Answer:

e. Will Jeremy ever catch up to Gerardo? If so, approximately when?
Answer:
Yes, Jeremy will catch up to Gerardo after about 24 minutes or about 3 miles.

f. At approximately what point do the graphs of the lines intersect?
Answer:
The lines intersect at approximately (24, 3).

Question 2.
Two cars drive from town A to town B at constant speeds. The blue car travels 25 miles per hour, and the red car travels 60 miles per hour. The blue car leaves at 9:30 a.m., and the red car leaves at noon. The distance between the two towns is 150 miles.
a. Who will get there first? Write and graph the system of linear equations that represents this situation.

Answer:
The linear equation that represents the distance traveled by the blue car is y = 25(x + 2.5), which is the same as y = 25x + 62.5. The linear equation that represents the distance traveled by the red car is
y = 60x. The system of linear equations that represents this situation is
y = 25x + 62.5
y = 60x

The red car will get to town B first.

b. At approximately what point do the graphs of the lines intersect?
Answer:
The lines intersect at approximately (1.8, 110).

Eureka Math Grade 8 Module 4 Lesson 24 Exit Ticket Answer Key

Question 1.
Darnell and Hector ride their bikes at constant speeds. Darnell leaves Hector’s house to bike home. He can bike the 8 miles in 32 minutes. Five minutes after Darnell leaves, Hector realizes that Darnell left his phone. Hector rides to catch up. He can ride to Darnell’s house in 24 minutes. Assuming they bike the same path, will Hector catch up to Darnell before he gets home?
a. Write the linear equation that represents Darnell’s constant speed.
Answer:
Darnell’s rate is \(\frac{1}{4}\) miles per minute. If he bikes y miles in x minutes at that constant speed, then y = \(\frac{1}{4}\) x.

b. Write the linear equation that represents Hector’s constant speed. Make sure to take into account that Hector left after Darnell.
Answer:
Hector’s rate is \(\frac{1}{3}\) miles per minute. If he bikes y miles in x minutes, then y = \(\frac{1}{3}\) x. To account for the extra time Darnell has to bike, we write the equation
y = \(\frac{1}{3}\) (x – 5)
y = \(\frac{1}{3}\) x-\(\frac{5}{3}\)

c. Write the system of linear equations that represents this situation.
Answer:
y = \(\frac{1}{4}\) x
y = \(\frac{1}{3}\) x-\(\frac{5}{3}\)

d. Sketch the graphs of the two equations.

Answer:

e. Will Hector catch up to Darnell before he gets home? If so, approximately when?
Answer:
Hector will catch up 20 minutes after Darnell left his house (or 15 minutes of biking by Hector) or approximately 5 miles.

f. At approximately what point do the graphs of the lines intersect?
Answer:
The lines intersect at approximately (20, 5).

Engage NY Eureka Math 8th Grade Module 4 Lesson 26 Answer Key

Eureka Math Grade 8 Module 4 Lesson 26 Exercise Answer Key

Exercises

Exercise 1.
Sketch the graphs of the system.
y = \(\frac{2}{3}\) x + 4
y = \(\frac{4}{6}\) x – 3

Answer:

a. Identify the slope of each equation. What do you notice?
Answer:
The slope of the first equation is \(\frac{2}{3}\), and the slope of the second equation is \(\frac{4}{6}\). The slopes are equal.

b. Identify the y – intercept point of each equation. Are the y – intercept points the same or different?
Answer:
The y – intercept points are (0,4) and (0, – 3). The y – intercept points are different.

Exercise 2.
Sketch the graphs of the system.
y = – \(\frac{5}{4}\) x + 7
y = – \(\frac{5}{4}\) x + 2

Answer:

a. Identify the slope of each equation. What do you notice?
Answer:
The slope of both equations is – \(\frac{5}{4}\). The slopes are equal.

b. Identify the y – intercept point of each equation. Are the y – intercept points the same or different?
Answer:
The y – intercept points are (0,7) and (0,2). The y – intercept points are different.

Exercise 3.
Sketch the graphs of the system.
y = 2x – 5
y = 2x – 1)

Answer:

a. Identify the slope of each equation. What do you notice?
Answer:
The slope of both equations is 2. The slopes are equal.

b. Identify the y – intercept point of each equation. Are the y – intercept points the same or different?
Answer:
The y – intercept points are (0, – 5) and (0, – 1). The y – intercept points are different.

Exercise 4.
Write a system of equations that has no solution.
Answer:
Answers will vary. Verify that the system that has been written has equations that have the same slope and unique y – intercept points. Sample student solution:

Exercise 5.
Write a system of equations that has (2,1) as a solution.
Answer:
Answers will vary. Verify that students have written a system where (2,1) is a solution to each equation. Sample student solution:

Exercise 6.
How can you tell if a system of equations has a solution or not?
Answer:
If the slopes of the equations are different, the lines will intersect at some point, and there will be a solution to the system. If the slopes of the equations are the same, and the y – intercept points are different, then the equations will graph as parallel lines, which means the system will not have a solution.

Exercise 7.
Does the system of linear equations shown below have a solution? Explain.
6x – 2y = 5
4x – 3y = 5
Answer:
Yes, this system does have a solution. The slope of the first equation is 3, and the slope of the second equation is \(\frac{4}{3}\). Since the slopes are different, these equations will graph as nonparallel lines, which means they will intersect at some point.

Exercise 8.
Does the system of linear equations shown below have a solution? Explain.
– 2x + 8y = 14
x = 4y + 1
Answer:
No, this system does not have a solution. The slope of the first equation is \(\frac{2}{8}\) = \(\frac{1}{4}\), and the slope of the second equation is \(\frac{1}{4}\). Since the slopes are the same, but the lines are distinct, these equations will graph as parallel lines. Parallel lines never intersect, which means this system has no solution.

Exercise 9.
Does the system of linear equations shown below have a solution? Explain.
12x + 3y = – 2
4x + y = 7
Answer:
No, this system does not have a solution. The slope of the first equation is – \(\frac{12}{3}\) = – 4, and the slope of the second equation is – 4. Since the slopes are the same, but the lines are distinct, these equations will graph as parallel lines. Parallel lines never intersect, which means this system has no solution.

Exercise 10.
Genny babysits for two different families. One family pays her $6 each hour and a bonus of $20 at the end of the night. The other family pays her $3 every half hour and a bonus of $25 at the end of the night. Write and solve the system of equations that represents this situation. At what number of hours do the two families pay the same for babysitting services from Genny?
Answer:
Let y represent the total amount Genny is paid for babysitting x hours. The first family pays y = 6x + 20. Since the other family pays by the half hour, 3∙2 would represent the amount Genny is paid each hour. So, the other family pays y = (3∙2)x + 25, which is the same as y = 6x + 25.
y = 6x + 20
y = 6x + 25
Since the equations in the system have the same slope and different y – intercept points, there will not be a point of intersection. That means that there will not be a number of hours for when Genny is paid the same amount by both families. The second family will always pay her $5 more than the first family.

Eureka Math Grade 8 Module 4 Lesson 26 Problem Set Answer Key

Answer Problems 1–5 without graphing the equations.
Question 1.
Does the system of linear equations shown below have a solution? Explain.
2x + 5y = 9
– 4x – 10y = 4
Answer:
No, this system does not have a solution. The slope of the first equation is – \(\frac{2}{5}\), and the slope of the second equation is – \(\frac{4}{10}\), which is equivalent to – \(\frac{2}{5}\). Since the slopes are the same, but the lines are distinct, these equations will graph as parallel lines. Parallel lines never intersect, which means this system has no solution.

Question 2.
Does the system of linear equations shown below have a solution? Explain.
\(\frac{3}{4}\) x – 3 = y
4x – 3y = 5
Answer:
Yes, this system does have a solution. The slope of the first equation is \(\frac{3}{4}\), and the slope of the second equation is \(\frac{4}{3}\). Since the slopes are different, these equations will graph as nonparallel lines, which means they will intersect at some point.

Question 3.
Does the system of linear equations shown below have a solution? Explain.
x + 7y = 8
7x – y = – 2
Answer:
Yes, this system does have a solution. The slope of the first equation is – \(\frac{1}{7}\), and the slope of the second equation is 7. Since the slopes are different, these equations will graph as nonparallel lines, which means they will intersect at some point.

Question 4.
Does the system of linear equations shown below have a solution? Explain.
y = 5x + 12
10x – 2y = 1
Answer:
No, this system does not have a solution. The slope of the first equation is 5, and the slope of the second equation is \(\frac{10}{2}\), which is equivalent to 5. Since the slopes are the same, but the lines are distinct, these equations will graph as parallel lines. Parallel lines never intersect, which means this system has no solution.

Question 5.
Does the system of linear equations shown below have a solution? Explain.
y = \(\frac{5}{3}\) x + 15
5x – 3y = 6
Answer:
No, this system does not have a solution. The slope of the first equation is \(\frac{5}{3}\), and the slope of the second equation is \(\frac{5}{3}\). Since the slopes are the same, but the lines are distinct, these equations will graph as parallel lines. Parallel lines never intersect, which means this system has no solution.

Question 6.
Given the graphs of a system of linear equations below, is there a solution to the system that we cannot see on this portion of the coordinate plane? That is, will the lines intersect somewhere on the plane not represented in the picture? Explain.

Answer:
The slope of l₁ is \(\frac{4}{7}\), and the slope of l₂ is \(\frac{6}{7}\). Since the slopes are different, these lines are nonparallel lines, which means they will intersect at some point. Therefore, the system of linear equations whose graphs are the given lines will have a solution.

Question 7.
Given the graphs of a system of linear equations below, is there a solution to the system that we cannot see on this portion of the coordinate plane? That is, will the lines intersect somewhere on the plane not represented in the picture? Explain.

Answer:
The slope of l₁ is – \(\frac{3}{8}\), and the slope of l₂ is – \(\frac{1}{2}\). Since the slopes are different, these lines are nonparallel lines, which means they will intersect at some point. Therefore, the system of linear equations whose graphs are the given lines will have a solution.

Question 8.
Given the graphs of a system of linear equations below, is there a solution to the system that we cannot see on this portion of the coordinate plane? That is, will the lines intersect somewhere on the plane not represented in the picture? Explain.

Answer:
The slope of l₁ is – 1, and the slope of l₂ is – 1. Since the slopes are the same the lines are parallel lines, which means they will not intersect. Therefore, the system of linear equations whose graphs are the given lines will have no solution.

Question 9.
Given the graphs of a system of linear equations below, is there a solution to the system that we cannot see on this portion of the coordinate plane? That is, will the lines intersect somewhere on the plane not represented in the picture? Explain.

Answer:
The slope of l₁ is \(\frac{1}{7}\), and the slope of l₂ is \(\frac{2}{11}\). Since the slopes are different, these lines are nonparallel lines, which means they will intersect at some point. Therefore, the system of linear equations whose graphs are the given lines will have a solution.

Question 10.
Given the graphs of a system of linear equations below, is there a solution to the system that we cannot see on this portion of the coordinate plane? That is, will the lines intersect somewhere on the plane not represented in the picture? Explain.

Answer:
Lines l₁ and l₁ are horizontal lines. That means that they are both parallel to the x – axis and, thus, are parallel to one another. Therefore, the system of linear equations whose graphs are the given lines will have no solution.

Eureka Math Grade 8 Module 4 Lesson 26 Exit Ticket Answer Key

Does each system of linear equations have a solution? Explain your answer.
Question 1.
y = \(\frac{5}{4}\) x – 3
y + 2 = \(\frac{5}{4}\) x
Answer:
No, this system does not have a solution. The slope of the first equation is \(\frac{5}{4}\) , and the slope of the second equation is \(\frac{5}{4}\). Since the slopes are the same, and they are distinct lines, these equations will graph as parallel lines. Parallel lines never intersect; therefore, this system has no solution.

Question 2.
y = \(\frac{2}{3}\) x – 5
4x – 8y = 11
Answer:
Yes, this system does have a solution. The slope of the first equation is \(\frac{2}{3}\), and the slope of the second equation is \(\frac{1}{2}\). Since the slopes are different, these equations will graph as nonparallel lines, which means they will intersect at some point.

Question 3.
\(\frac{1}{3}\) x + y = 8
x + 3y = 12
Answer:
No, this system does not have a solution. The slope of the first equation is – \(\frac{1}{3}\), and the slope of the second equation is – \(\frac{1}{3}\). Since the slopes are the same, and they are distinct lines, these equations will graph as parallel lines. Parallel lines never intersect; therefore, this system has no solution.

Engage NY Eureka Math 8th Grade Module 4 Lesson 28 Answer Key

Eureka Math Grade 8 Module 4 Lesson 28 Example Answer Key

Example 1.
Use what you noticed about adding equivalent expressions to solve the following system by elimination:
6x – 5y = 21
2x + 5y = – 5
Answer:
Show students the three examples of adding integer equations together. Ask students to verbalize what they notice in the examples and to generalize what they observe. The goal is for students to see that they can add equivalent expressions and still have an equivalence.
Example 1: If 2 + 5 = 7 and 1 + 9 = 10, does 2 + 5 + 1 + 9 = 7 + 10?
Example 2: If 1 + 5 = 6 and 7 – 2 = 5, does 1 + 5 + 7 – 2 = 6 + 5?
Example 3: If – 3 + 11 = 8 and 2 + 1 = 3, does – 3 + 11 + 2 + 1 = 8 + 3?
Use what you noticed about adding equivalent expressions to solve the following system by elimination:
6x – 5y = 21
2x + 5y = – 5

Provide students with time to attempt to solve the system by adding the equations together. Have students share their work with the class. If necessary, use the points belows to support students.
Notice that terms – 5y and 5y are opposites; that is, they have a sum of zero when added. If we were to add the equations in the system, the y would be eliminated.
6x – 5y + 2x + 5y = 21 + ( – 5)
6x + 2x – 5y + 5y = 16
8x = 16
x = 2
Just as before, now that we know what x is, we can substitute it into either equation to determine the value of y.
2(2) + 5y = – 5
4 + 5y = – 5
5y = – 9
y = – \(\frac{9}{5}\)
The solution to the system is (2, – \(\frac{9}{5}\)).
We can verify our solution by sketching the graphs of the system.

Example 2.
Solve the following system by elimination:
– 2x + 7y = 5
4x – 2y = 14
Answer:
We will solve the following system by elimination:
– 2x + 7y = 5
4x – 2y = 14

In this example, it is not as obvious which variable to eliminate. It will become obvious as soon as we multiply the first equation by 2.
2( – 2x + 7y = 5)
– 4x + 14y = 10
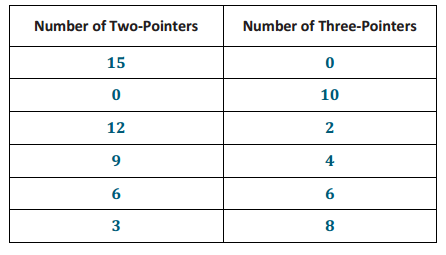
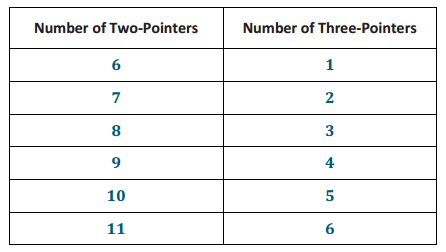
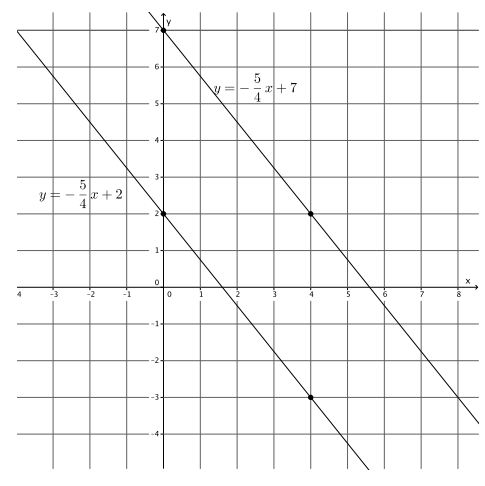
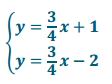
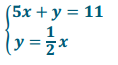
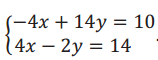Now we have the system . It is clear that when we add – 4x + 4x, the x will be eliminated. Add the equations of this system together, and determine the solution to the system.
Sample student work:
– 4x + 14y + 4x – 2y = 10 + 14
14y – 2y = 24
12y = 24
y = 2

4x – 2(2) = 14
4x – 4 = 14
4x = 18
x = \(\frac{18}{4}\)
x = \(\frac{9}{2}\)
The solution to the system is (\(\frac{9}{2}\), 2).
We can verify our solution by sketching the graphs of the system.

Example 3.
Solve the following system by elimination:
7x – 5y = – 2
3x – 3y = 7
Answer:
We will solve the following system by elimination:
7x – 5y = – 2
3x – 3y = 7

Provide time for students to solve this system on their own before discussing it as a class.
In this case, it is even less obvious which variable to eliminate. On these occasions, we need to rewrite both equations. We multiply the first equation by – 3 and the second equation by 7.
– 3(7x – 5y = – 2)
– 21x + 15y = 6

7(3x – 3y = 7)
21x – 21y = 49
Now we have the system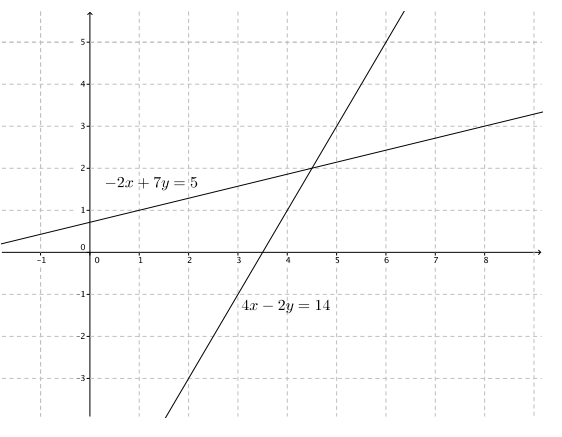 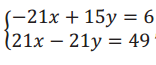, and it is obvious that the x can be eliminated.
Look at the system again.
7x – 5y = – 2
3x – 3y = 7

What would we do if we wanted to eliminate the y from the system?
We could multiply the first equation by 3 and the second equation by – 5.
Students may say to multiply the first equation by – 3 and the second equation by 5. Whichever answer is given first, ask if the second is also a possibility. Students should answer yes. Then have students solve the system.
Sample student work:
– 21x + 15y = 6
21x – 21y = 49

15y – 21y = 6 + 49
– 6y = 55
y = – \(\frac{55}{6}\)
7x – 5( – \(\frac{55}{6}\)) = – 2
7x + \(\frac{275}{6}\) = – 2
7x = – \(\frac{287}{6}\)
x = – \(\frac{287}{42}\)
The solution to the system is ( – \(\frac{287}{42}\), – \(\frac{55}{6}\)).

Eureka Math Grade 8 Module 4 Lesson 28 Exercise Answer Key

Exercises
Each of the following systems has a solution. Determine the solution to the system by eliminating one of the variables. Verify the solution using the graph of the system.
Exercise 1.
6x – 7y = – 10
3x + 7y = – 8
Answer:
6x – 7y + 3x + 7y = – 10 + ( – 8)
9x = – 18
x = – 2
3( – 2) + 7y = – 8
– 6 + 7y = – 8
7y = – 2
y = – \(\frac{2}{7}\)
The solution is ( – 2, – \(\frac{2}{7}\)).

Exercise 2.
x – 4y = 7
5x + 9y = 6
Answer:
– 5(x – 4y = 7)
– 5x + 20y = – 35

– 5x + 20y = – 35
5x + 9y = 6

– 5x + 20y + 5x + 9y = – 35 + 6
29y = – 29
y = – 1
x – 4( – 1) = 7
x + 4 = 7
x = 3
The solution is (3, – 1).

Exercise 3.
2x – 3y = – 5
3x + 5y = 1
Answer:
– 3(2x – 3y = – 5)
– 6x + 9y = 15
2(3x + 5y = 1)
6x + 10y = 2

– 6x + 9y = 15
6x + 10y = 2

– 6x + 9y + 6x + 10y = 15 + 2
19y = 17
y = \(\frac{17}{19}\)
2x – 3(\(\frac{17}{19}\)) = – 5
2x – \(\frac{51}{19}\) = – 5
2x = – 5 + \(\frac{51}{19}\)
2x = – \(\frac{44}{19}\)
x = – \(\frac{44}{38}\)
x = – \(\frac{22}{19}\)
The solution is ( – \(\frac{22}{19}\), \(\frac{17}{19}\)).

Eureka Math Grade 8 Module 4 Lesson 28 Problem Set Answer Key

Determine the solution, if it exists, for each system of linear equations. Verify your solution on the coordinate plane.
Question 1.
\(\frac{1}{2}\) x + 5 = y
2x + y = 1
Answer:
2x + \(\frac{1}{2}\) x + 5 = 1
\(\frac{5}{2}\) x + 5 = 1
\(\frac{5}{2}\) x = – 4
x = – \(\frac{8}{5}\)
2( – \(\frac{8}{5}\)) + y = 1
– \(\frac{16}{5}\) + y = 1
y = \(\frac{21}{5}\)
The solution is ( – \(\frac{8}{5}\), \(\frac{21}{5}\)).

Question 2.
9x + 2y = 9
– 3x + y = 2
Answer:
3( – 3x + y = 2)
– 9x + 3y = 6

9x + 2y = 9
– 9x + 3y = 6

9x + 2y – 9x + 3y = 15
5y = 15
y = 3
– 3x + 3 = 2
– 3x = – 1
x = \(\frac{1}{3}\)
The solution is (\(\frac{1}{3}\), 3).

Question 3.
y = 2x – 2
2y = 4x – 4
Answer:
These equations define the same line. Therefore, this system will have infinitely many solutions.

Question 4.
8x + 5y = 19
– 8x + y = – 1
Answer:
8x + 5y – 8x + y = 19 – 1
5y + y = 18
6y = 18
y = 3
8x + 5(3) = 19
8x + 15 = 19
8x = 4
x = \(\frac{1}{2}\)
The solution is (\(\frac{1}{2}\), 3)

Question 5.
x + 3 = y
3x + 4y = 7
Answer:
3x + 4(x + 3) = 7
3x + 4x + 12 = 7
7x + 12 = 7
7x = – 5
x = – \(\frac{5}{7}\)
– \(\frac{5}{7}\) + 3 = y
\(\frac{16}{7}\) = y
The solution is ( – \(\frac{5}{7}\), \(\frac{16}{7}\)).

Question 6.
y = 3x + 2
4y = 12 + 12x
Answer:
The equations graph as distinct lines. The slopes of these two equations are the same, and the y – intercept points are different, which means they graph as parallel lines. Therefore, this system will have no solution.

Question 7.
4x – 3y = 16
– 2x + 4y = – 2
Answer:
2( – 2x + 4y = – 2)
– 4x + 8y = – 4

4x – 3y = 16
– 4x + 8y = – 4

4x – 3y – 4x + 8y = 16 – 4
– 3y + 8y = 12
5y = 12
y = \(\frac{12}{5}\)
4x – 3(\(\frac{12}{5}\)) = 16
4x – \(\frac{36}{5}\) = 16
4x = \(\frac{116}{5}\)
x = \(\frac{29}{5}\)
The solution is (\(\frac{29}{5}\), \(\frac{12}{5}\)).

Question 8.
2x + 2y = 4
12 – 3x = 3y
Answer:
The equations graph as distinct lines. The slopes of these two equations are the same, and the y – intercept points are different, which means they graph as parallel lines. Therefore, this system will have no solution.

Question 9.
y = – 2x + 6
3y = x – 3
Answer:
3(y = – 2x + 6)
3y = – 6x + 18

3y = – 6x + 18
3y = x – 3

– 6x + 18 = x – 3
18 = 7x – 3
21 = 7x
\(\frac{21}{7}\) = x
x = 3
y = – 2(3) + 6
y = – 6 + 6
y = 0
The solution is (3, 0).

Question 10.
y = 5x – 1
10x = 2y + 2
Answer:
These equations define the same line. Therefore, this system will have infinitely many solutions.

Question 11.
3x – 5y = 17
6x + 5y = 10
Answer:
3x – 5y + 6x + 5y = 17 + 10
9x = 27
x = 3
3(3) – 5y = 17
9 – 5y = 17
– 5y = 8
y = – \(\frac{8}{5}\)
The solution is (3, – \(\frac{8}{5}\)).

Question 12.
y = \(\frac{4}{3}\) x – 9
y = x + 3
Answer:
\(\frac{4}{3}\) x – 9 = x + 3
\(\frac{1}{3}\) x – 9 = 3
\(\frac{1}{3}\) x = 12
x = 36
y = 36 + 3
y = 39
The solution is (36, 39).

Question 13.
4x – 7y = 11
x + 2y = 10
Answer:
– 4(x + 2y = 10)
– 4x – 8y = – 40

4x – 7y = 11
– 4x – 8y = – 40

4x – 7y – 4x – 8y = 11 – 40
– 15y = – 29
y = \(\frac{29}{15}\)
x + 2(\(\frac{29}{15}\)) = 10
x + \(\frac{58}{15}\) = 10
x = \(\frac{92}{15}\)
The solution is (\(\frac{92}{15}\), \(\frac{29}{15}\)).

Question 14.
21x + 14y = 7
12x + 8y = 16
Answer:
The slopes of these two equations are the same, and the y – intercept points are different, which means they graph as parallel lines. Therefore, this system will have no solution.

Answer:

Eureka Math Grade 8 Module 4 Lesson 28 Exit Ticket Answer Key

Determine the solution, if it exists, for each system of linear equations. Verify your solution on the coordinate plane.
Question 1.
y = 3x – 5
y = – 3x + 7

Answer:
3x – 5 = – 3x + 7
6x = 12
x = 2
y = 3(2) – 5
y = 6 – 5
y = 1
The solution is (2, 1).

Question 2.
y = – 4x + 6
2x – y = 11

Answer:
2x – ( – 4x + 6) = 11
2x + 4x – 6 = 11
6x = 17
x = \(\frac{17}{6}\)
y = – 4(\(\frac{17}{6}\)) + 6
y = – \(\frac{34}{3}\) + 6
y = – \(\frac{16}{3}\)
The solution is (\(\frac{17}{6}\), – \(\frac{16}{3}\)).

Engage NY Eureka Math 8th Grade Module 4 Lesson 27 Answer Key

Eureka Math Grade 8 Module 4 Lesson 27 Exercise Answer Key

Exercises
Determine the nature of the solution to each system of linear equations.

Exercise 1.
3x + 4y = 5
y = – \(\frac{3}{4}\) x + 1
Answer:
The slopes of these two distinct equations are the same, which means the graphs of these two equations are parallel lines. Therefore, this system will have no solution.

Exercise 2.
7x + 2y = – 4
x – y = 5
Answer:
The slopes of these two equations are different. That means the graphs of these two equations are distinct nonparallel lines and will intersect at one point. Therefore, this system has one solution.

Exercise 3.
9x + 6y = 3
3x + 2y = 1
Answer:
The lines defined by the graph of this system of equations are the same line because they have the same slope and the same y – intercept point.

Determine the nature of the solution to each system of linear equations. If the system has a solution, find it algebraically, and then verify that your solution is correct by graphing.
Exercise 4.
3x + 3y = – 21
x + y = – 7
Answer:
These equations define the same line. Therefore, this system will have infinitely many solutions.

Exercise 5.
y = \(\frac{3}{2}\) x – 1
3y = x + 2
Answer:
The slopes of these two equations are unique. That means they graph as distinct lines and will intersect at one point. Therefore, this system has one solution.
3(y = \(\frac{3}{2}\) x – 1)
3y = \(\frac{9}{2}\) x – 3
x + 2 = \(\frac{9}{2}\) x – 3
2 = \(\frac{7}{2}\) x – 3
5 = \(\frac{7}{2}\) x
\(\frac{10}{7}\) = x
y = \(\frac{3}{2}\) (\(\frac{10}{7}\)) – 1
y = \(\frac{15}{7}\) – 1
y = \(\frac{8}{7}\)
The solution is (\(\frac{10}{7}\), \(\frac{8}{7}\)).

Exercise 6.
x = 12y – 4
x = 9y + 7
Answer:
The slopes of these two equations are unique. That means they graph as distinct lines and will intersect at one point. Therefore, this system has one solution.
12y – 4 = 9y + 7
3y – 4 = 7
3y = 11
y = \(\frac{11}{3}\)
x = 9(\(\frac{11}{3}\)) + 7
x = 33 + 7
x = 40
The solution is (40, \(\frac{11}{3}\)).

Exercise 7.
Write a system of equations with (4, – 5) as its solution.
Answer:
Answers will vary. Verify that students have written a system of equations where (4, – 5) is a solution to each equation in the system.
Sample solution:

Eureka Math Grade 8 Module 4 Lesson 27 Problem Set Answer Key

Determine the nature of the solution to each system of linear equations. If the system has a solution, find it algebraically, and then verify that your solution is correct by graphing.
Question 1.
y = \(\frac{3}{7}\) x – 8
3x – 7y = 1
Answer:
The slopes of these two equations are the same, and the y – intercept points are different, which means they graph as parallel lines. Therefore, this system will have no solution.

Question 2.
2x – 5 = y
– 3x – 1 = 2y
Answer:
(2x – 5 = y)²
4x – 10 = 2y

4x – 10 = 2y
– 3x – 1 = 2y

4x – 10 = – 3x – 1
7x – 10 = – 1
7x = 9
x = \(\frac{9}{7}\)
y = 2(\(\frac{9}{7}\)) – 5
y = \(\frac{18}{7}\) – 5
y = – \(\frac{17}{7}\)
The solution is (\(\frac{9}{7}\), – \(\frac{17}{7}\)).

Question 3.
x = 6y + 7
x = 10y + 2
Answer:
6y + 7 = 10y + 2
7 = 4y + 2
5 = 4y
\(\frac{5}{4}\) = y
x = 6(\(\frac{5}{4}\)) + 7
x = \(\frac{15}{2}\) + 7
x = \(\frac{29}{2}\)
The solution is (\(\frac{29}{2}\), \(\frac{5}{4}\)).

Question 4.
5y = \(\frac{15}{4}\) x + 25
y = \(\frac{3}{4}\) x + 5
Answer:
These equations define the same line. Therefore, this system will have infinitely many solutions.

Question 5.
x + 9 = y
x = 4y – 6
Answer:
4y – 6 + 9 = y
4y + 3 = y
3 = – 3y
– 1 = y x + 9 = – 1
x = – 10
The solution is ( – 10, – 1).

Question 6.
3y = 5x – 15
3y = 13x – 2
Answer:
5x – 15 = 13x – 2
– 15 = 8x – 2
– 13 = 8x
– \(\frac{13}{8}\) = x
3y = 5( – \(\frac{13}{8}\)) – 15
3y = – \(\frac{65}{8}\) – 15
3y = – \(\frac{185}{8}\)
y = – \(\frac{185}{24}\)
The solution is ( – \(\frac{13}{8}\), – \(\frac{185}{24}\)).

Question 7.
6x – 7y = \(\frac{1}{2}\)
12x – 14y = 1
Answer:
These equations define the same line. Therefore, this system will have infinitely many solutions.

Question 8.
5x – 2y = 6
– 10x + 4y = – 14
Answer:
The slopes of these two equations are the same, and the y – intercept points are different, which means they graph as parallel lines. Therefore, this system will have no solution.

Question 9.
y = \(\frac{3}{2}\) x – 6
2y = 7 – 4x
Answer:
2(y = \(\frac{3}{2}\) x – 6)
2y = 3x – 12

2y = 3x – 12
2y = 7 – 4x
3x – 12 = 7 – 4x
7x – 12 = 7
7x = 19
x = \(\frac{19}{7}\)
y = \(\frac{3}{2}\) (\(\frac{19}{7}\)) – 6
y = \(\frac{57}{14}\) – 6
y = – \(\frac{27}{14}\)
The solution is (\(\frac{19}{7}\), – \(\frac{27}{14}\)).

Question 10.
7x – 10 = y
y = 5x + 12
Answer:
7x – 10 = 5x + 12
2x – 10 = 12
2x = 22
x = 11
y = 5(11) + 12
y = 55 + 12
y = 67
The solution is (11, 67).

Question 11.
Write a system of linear equations with ( – 3, 9) as its solution.
Answer:
Answers will vary. Verify that students have written a system of equations where ( – 3, 9) is a solution to each equation in the system. Sample solution:

Eureka Math Grade 8 Module 4 Lesson 27 Exit Ticket Answer Key

Determine the nature of the solution to each system of linear equations. If the system has a solution, then find it without graphing.
Question 1.
y = \(\frac{1}{2}\) x + \(\frac{5}{2}\)
x – 2y = 7
Answer:
The slopes of these two equations are the same, and the y – intercept points are different, which means they graph as parallel lines. Therefore, this system will have no solution.

Question 2.
y = \(\frac{2}{3}\) x + 4
2y + \(\frac{1}{2}\) x = 2
Answer:
The slopes of these two equations are unique. That means they graph as distinct lines and will intersect at one point. Therefore, this system has one solution.
2(\(\frac{2}{3}\) x + 4) + \(\frac{1}{2}\) x = 2
\(\frac{4}{3}\) x + 8 + \(\frac{1}{2}\) x = 2
\(\frac{11}{6}\) x + 8 = 2
\(\frac{11}{6}\) x = – 6
x = – \(\frac{36}{11}\)
y = \(\frac{2}{3}\) ( – \(\frac{36}{11}\)) + 4
y = – \(\frac{24}{11}\) + 4
y = \(\frac{20}{11}\)
The solution is ( – \(\frac{36}{11}\), \(\frac{20}{11}\)).

Question 3.
y = 3x – 2
– 3x + y = – 2
Answer:
These equations define the same line. Therefore, this system will have infinitely many solutions.

Engage NY Eureka Math 8th Grade Module 4 Lesson 29 Answer Key

Eureka Math Grade 8 Module 4 Lesson 29 Example Answer Key

Example 1.
The sum of two numbers is 361, and the difference between the two numbers is 173. What are the two numbers?
Answer:
→ Together, we will read a word problem and work toward finding the solution.
→ The sum of two numbers is 361, and the difference between the two numbers is 173. What are the two numbers?
Provide students time to work independently or in pairs to solve this problem. Have students share their solutions and explain how they arrived at their answers. Then, show how the problem can be solved using a system of linear equations.

→ What do we need to do first?
We need to define our variables.
→ If we define our variables, we can better represent the situation we have been given. What should the variables be for this problem?
Let x represent one number, and let y represent the other number.
→ Now that we know the numbers are x and y, what do we need to do now?
We need to write equations to represent the information in the word problem.
→ Using x and y, write equations to represent the information we are provided.
The sum of two numbers is 361 can be written as x + y = 361. The difference between the two numbers is 173 can be written as x – y = 173.

→ We have two equations to represent this problem. What is it called when we have more than one linear equation for a problem, and how is it represented symbolically?
We have a system of linear equations.
x + y = 361
x – y = 173

→ We know several methods for solving systems of linear equations. Which method do you think will be the most efficient, and why?
We should add the equations together to eliminate the variable y because we can do that in one step.
Solve the system:
x + y = 361
x – y = 173
Sample student work:
x + y = 361
x – y = 173
x + x + y – y = 361 + 173
2x = 534
x = 267
267 + y = 361
y = 94
The solution is (267, 94).

→ Based on our work, we believe the two numbers are 267 and 94. Check to make sure your answer is correct by substituting the numbers into both equations. If it makes a true statement, then we know we are correct. If it makes a false statement, then we need to go back and check our work.
Sample student work:
267 + 94 = 361
361 = 361
267 – 94 = 173
173 = 173

→ Now we are sure that the numbers are 267 and 94. Does it matter which number is x and which number is y?
Not necessarily, but we need their difference to be positive, so x must be the larger of the two numbers to make sense of our equation x – y = 173.

Example 2.
There are 356 eighth – grade students at Euclid’s Middle School. Thirty – four more than four times the number of girls is equal to half the number of boys. How many boys are in eighth grade at Euclid’s Middle School? How many girls?
Answer:
→ Again, we will work together to solve the following word problem.
→ There are 356 eighth – grade students at Euclid’s Middle School. Thirty – four more than four times the number of girls is equal to half the number of boys. How many boys are in eighth grade at Euclid’s Middle School? How many girls? What do we need to do first?
We need to define our variables.

→ If we define our variables, we can better represent the situation we have been given. What should the variables be for this problem?
Let x represent the number of girls, and let y represent the number of boys.
Whichever way students define the variables, ask them if it could be done the opposite way. For example, if students respond as stated above, ask them if we could let x represent the number of boys and y represent the number of girls. They should say that at this stage it does not matter if x represents girls or boys, but once the variable is defined, it does matter.

→ Now that we know that x is the number of girls and y is the number of boys, what do we need to do now?
We need to write equations to represent the information in the word problem.
→ Using x and y, write equations to represent the information we are provided.
There are 356 eighth – grade students can be represented as x + y = 356. Thirty – four more than four times the number of girls is equal to half the number of boys can be represented as 4x + 34 = \(\frac{1}{2}\) y.
→ We have two equations to represent this problem. What is it called when we have more than one linear equation for a problem, and how is it represented symbolically?
We have a system of linear equations.
x + y = 356
4x + 34 = \(\frac{1}{2}\) y

→ We know several methods for solving systems of linear equations. Which method do you think will be the most efficient and why?
Answers will vary. There is no obvious “most efficient” method. Accept any reasonable responses as long as they are justified.
Solve the system:
x + y = 356
4x + 34 = \(\frac{1}{2}\) y

Sample student work:
x + y = 356
4x + 34 = \(\frac{1}{2}\) y

2(4x + 34 = \(\frac{1}{2}\) y)
8x + 68 = y
x + y = 356
8x + 68 = y
x + 8x + 68 = 356
9x + 68 = 356
9x = 288
x = 32
32 + y = 356
y = 324
The solution is (32, 324).

→ What does the solution mean in context?
Since we let x represent the number of girls and y represent the number of boys, it means that there are 32 girls and 324 boys at Euclid’s Middle School in eighth grade.
→ Based on our work, we believe there are 32 girls and 324 boys. How can we be sure we are correct?
We need to substitute the values into both equations of the system to see if it makes a true statement.
32 + 324 = 356
356 = 356
4(32) + 34 = \(\frac{1}{2}\) (324)
128 + 34 = 162
162 = 162

Example 3.
A family member has some five – dollar bills and one – dollar bills in her wallet. Altogether she has 18 bills and a total of $62. How many of each bill does she have?
Answer:
→ Again, we will work together to solve the following word problem.
→ A family member has some five – dollar bills and one – dollar bills in her wallet. Altogether she has 18 bills and a total of $62. How many of each bill does she have? What do we do first?
We need to define our variables.

→ If we define our variables, we can better represent the situation we have been given. What should the variables be for this problem?
Let x represent the number of $5 bills, and let y represent the number of $1 bills.
Again, whichever way students define the variables, ask them if it could be done the opposite way.
→ Now that we know that x is the number of $5 bills and y is the number of $1 bills, what do we need to do now?
We need to write equations to represent the information in the word problem.

→ Using x and y, write equations to represent the information we are provided.
Altogether she has 18 bills and a total of $62 must be represented with two equations, the first being x + y = 18 to represent the total of 18 bills and the second being 5x + y = 62 to represent the total amount of money she has.
→ We have two equations to represent this problem. What is it called when we have more than one linear equation for a problem, and how is it represented symbolically?
We have a system of linear equations.
x + y = 18
5x + y = 62
→ We know several methods for solving systems of linear equations. Which method do you think will be the most efficient and why?
Answers will vary. Students might say they could multiply one of the equations by – 1, and then they would be able to eliminate the variable y when they add the equations together. Other students may say it would be easiest to solve for y in the first equation and then substitute the value of y into the second equation. After they have justified their methods, allow them to solve the system in any manner they choose.

→ Solve the system:
x + y = 18
5x + y = 62
Sample student work:
x + y = 18
5x + y = 62

x + y = 18
y = – x + 18

y = – x + 18
5x + y = 62

5x + ( – x) + 18 = 62
4x + 18 = 62
4x = 44
x = 11

11 + y = 18
y = 7
The solution is (11, 7).
→ What does the solution mean in context?
Since we let x represent the number of $5 bills and y represent the number of $1 bills, it means that the family member has 11 $5 bills, and 7 $1 bills.
→ The next step is to check our work.
It is obvious that 11 + 7 = 18, so we know the family member has 18 bills.
→ It makes more sense to check our work against the actual value of those 18 bills in this case. Now we check the second equation.
5(11) + 1(7) = 62
55 + 7 = 62
62 = 62

Example 4.
A friend bought 2 boxes of pencils and 8 notebooks for school, and it cost him $11. He went back to the store the same day to buy school supplies for his younger brother. He spent $11.25 on 3 boxes of pencils and 5 notebooks. How much would 7 notebooks cost?
Answer:
Solve the system:
2x + 8y = 11
3x + 5y = 11.25.
Sample student work:
2x + 8y = 11
3x + 5y = 11.25
3(2x + 8y = 11)
6x + 24y = 33
– 2(3x + 5y = 11.25)
– 6x – 10y = – 22.50

6x + 24y = 33
– 6x – 10y = – 22.50

6x + 24y – 6x – 10y = 33 – 22.50
24y – 10y = 10.50
14y = 10.50
y = \(\frac{10.50}{14}\)
y = 0.75

2x + 8(0.75) = 11
2x + 6 = 11
2x = 5
x = 2.50
The solution is (2.50, 0.75).
→ What does the solution mean in context?
It means that a box of pencils costs $2.50, and a notebook costs $0.75.
→ Before we answer the question that this word problem asked, check to make sure the solution is correct.
Sample student work:
2(2.50) + 8(0.75) = 11
5 + 6 = 11
11 = 11
3(2.50) + 5(0.75) = 11.25
7.50 + 3.75 = 11.25
11.25 = 11.25
→ Now that we know we have the correct costs for the box of pencils and notebooks, we can answer the original question: How much would 7 notebooks cost?
The cost of 7 notebooks is 7(0.75) = 5.25. Therefore, 7 notebooks cost $7.25.

→ Keep in mind that some word problems require us to solve the system in order to answer a specific question, like this example about the cost of 7 notebooks. Other problems may just require the solution to the system to answer the word problem, like the first example about the two numbers and their sum and difference. It is always a good practice to reread the word problem to make sure you know what you are being asked to do.

Eureka Math Grade 8 Module 4 Lesson 29 Exercise Answer Key

Exercises

Exercise 1.
A farm raises cows and chickens. The farmer has a total of 42 animals. One day he counts the legs of all of his animals and realizes he has a total of 114. How many cows does the farmer have? How many chickens?
Answer:
Let x represent the number of cows and y represent the number of chickens. Then:
x + y = 42
4x + 2y = 114
– 2(x + y = 42)
– 2x – 2y = – 84

– 2x – 2y = – 84
4x + 2y = 114
– 2x – 2y + 4x + 2y = – 84 + 114
– 2x + 4x = 30
2x = 30
x = 15
15 + y = 42
y = 27
The solution is (15, 27).
4(15) + 2(27) = 114
60 + 54 = 114
114 = 114
The farmer has 15 cows and 27 chickens.

Exercise 2.
The length of a rectangle is 4 times the width. The perimeter of the rectangle is 45 inches. What is the area of the rectangle?
Answer:
Let x represent the length and y represent the width. Then:
x = 4y
2x + 2y = 45
2(4y) + 2y = 45
8y + 2y = 45
10y = 45
y = 4.5
x = 4(4.5)
x = 18
The solution is (18, 4.5).
2(18) + 2(4.5) = 45
36 + 9 = 45
45 = 45
Since 18×4.5 = 81, the area of the rectangle is 81 in^2.

Exercise 3.
The sum of the measures of angles x and y is 127°. If the measure of ∠x is 34° more than half the measure of ∠y, what is the measure of each angle?
Answer:
Let x represent the measure of ∠x and y represent the measure of ∠y. Then:
x + y = 127
x = 34 + \(\frac{1}{2}\) y
34 + \(\frac{1}{2}\) y + y = 127
34 + \(\frac{3}{2}\) y = 127
\(\frac{3}{2}\) y = 93
y = 62
x + 62 = 127
x = 65
The solution is (65,62).
65 = 34 + \(\frac{1}{2}\) (62)
65 = 34 + 31
65 = 65
The measure of ∠x is 65°, and the measure of ∠y is 62°.

Eureka Math Grade 8 Module 4 Lesson 29 Problem Set Answer Key

Question 1.
Two numbers have a sum of 1,212 and a difference of 518. What are the two numbers?
Answer:
Let x represent one number and y represent the other number.
x + y = 1212
x – y = 518
x + y + x – y = 1212 + 518
2x = 1730
x = 865
865 + y = 1212
y = 347
The solution is (865, 347).
865 – 347 = 518
518 = 518
The two numbers are 347 and 865.

Question 2.
The sum of the ages of two brothers is 46. The younger brother is 10 more than a third of the older brother’s age. How old is the younger brother?
Answer:
Let x represent the age of the younger brother and y represent the age of the older brother.
x + y = 46
x = 10 + \(\frac{1}{3}\) y
10 + \(\frac{1}{3}\) y + y = 46
10 + \(\frac{4}{3}\) y = 46
\(\frac{4}{3}\) y = 36
y = 27
x + 27 = 46
x = 19
The solution is (19,27).
19 = 10 + \(\frac{1}{3}\) (27)
19 = 10 + 9
19 = 19
The younger brother is 19 years old.

Question 3.
One angle measures 54 more degrees than 3 times another angle. The angles are supplementary. What are their measures?
Answer:
Let x represent the measure of one angle and y represent the measure of the other angle.
x = 3y + 54
x + y = 180
3y + 54 + y = 180
4y + 54 = 180
4y = 126
y = 31.5
x = 3(31.5) + 54
x = 94.5 + 54
x = 148.5
The solution is ( 148.5, 31.5).
148.5 + 31.5 = 180
180 = 180
One angle measures 148.5°, and the other measures 31.5°.

Question 4.
Some friends went to the local movie theater and bought four large buckets of popcorn and six boxes of candy. The total for the snacks was $46.50. The last time you were at the theater, you bought a large bucket of popcorn and a box of candy, and the total was $9.75. How much would 2 large buckets of popcorn and 3 boxes of candy cost?
Answer:
Let x represent the cost of a large bucket of popcorn and y represent the cost of a box of candy.
4x + 6y = 46.50
x + y = 9.75
– 4(x + y = 9.75)
– 4x – 4y = – 39

4x + 6y = 46.50
– 4x – 4y = – 39
4x + 6y – 4x – 4y = 46.50 – 39
6y – 4y = 7.50
2y = 7.50
y = 3.75
x + 3.75 = 9.75
x = 6
The solution is (6, 3.75).
4(6) + 6(3.75) = 46.50
24 + 22.50 = 46.50
46.50 = 46.50
Since one large bucket of popcorn costs $6 and one box of candy costs $3.75, then
2(6) + 3(3.75) = 12 + 11.25 = 23.25, and two large buckets of popcorn and three boxes of candy will cost $23.25.

Question 5.
You have 59 total coins for a total of $12.05. You only have quarters and dimes. How many of each coin do you have?
Answer:
Let x represent the number of quarters and y represent the number of dimes.
x + y = 59
0.25x + 0.1y = 12.05

– 4(0.25x + 0.1y = 12.05)
– x – 0.4y = – 48.20

x + y = 59
– x – 0.4y = – 48.20

x + y – x – 0.4y = 59 – 48.20
y – 0.4y = 10.80
0.6y = 10.80
y = \(\frac{10.80}{0.6}\)
y = 18
x + 18 = 59
x = 41
The solution is (41,18).
0.25(41) + 0.1(18) = 12.05
10.25 + 1.80 = 12.05
12.05 = 12.05
I have 41 quarters and 18 dimes.

Question 6.
A piece of string is 112 inches long. Isabel wants to cut it into 2 pieces so that one piece is three times as long as the other. How long is each piece?
Answer:
Let x represent one piece and y represent the other.
x + y = 112
3y = x

3y + y = 112
4y = 112
y = 28
x + 28 = 112
x = 84
The solution is (84, 28).
3(28) = 84
84 = 84
One piece should be 84 inches long, and the other should be 28 inches long.

Eureka Math Grade 8 Module 4 Lesson 29 Exit Ticket Answer Key

Question 1.
Small boxes contain DVDs, and large boxes contain one gaming machine. Three boxes of gaming machines and a box of DVDs weigh 48 pounds. Three boxes of gaming machines and five boxes of DVDs weigh 72 pounds. How much does each box weigh?
Answer:
Let x represent the weight of the gaming machine box, and let y represent the weight of the DVD box. Then:
3x + y = 48
3x + 5y = 72
– 1(3x + y = 48)
– 3x – y = – 48

– 3x – y = – 48
3x + 5y = 72
3x – 3x + 5y – y = 72 – 48
4y = 24
y = 6
3x + 6 = 48
3x = 42
x = 14
The solution is (14, 6).
3(14) + 5(6) = 72
72 = 72
The box with one gaming machine weighs 14 pounds, and the box containing DVDs weighs 6 pounds.

Question 2.
A language arts test is worth 100 points. There is a total of 26 questions. There are spelling word questions that are worth 2 points each and vocabulary word questions worth 5 points each. How many of each type of question are there?
Answer:
Let x represent the number of spelling word questions, and let y represent the number of vocabulary word questions.
x + y = 26
2x + 5y = 100
– 2(x + y = 26)
– 2x – 2y = – 52

– 2x – 2y = – 52
2x + 5y = 100
2x – 2x + 5y – 2y = 100 – 52
3y = 48
y = 16
x + 16 = 26
x = 10
The solution is (10, 16).
2(10) + 5(16) = 100
100 = 100
There are 10 spelling word questions and 16 vocabulary word questions.

Engage NY Eureka Math 8th Grade Module 4 Lesson 30 Answer Key

Eureka Math Grade 8 Module 4 Lesson 30 Exercise Answer Key

Mathematical Modeling Exercise
(1) If t is a number, what is the degree in Fahrenheit that corresponds to t°C?
(2) If t is a number, what is the degree in Fahrenheit that corresponds to ( – t)°C?
Answer:
→ Instead of trying to answer these questions directly, let’s try something simpler. With this in mind, can we find out what degree in Fahrenheit corresponds to 1°C? Explain.
→ We can use the following diagram (double number line) to organize our thinking.

Answer:
→ At this point, the only information we have is that 0°C = 32°F, and 100°C = 212°F. We want to figure out what degree of Fahrenheit corresponds to 1°C. Where on the diagram would 1°C be located? Be specific.

Provide students time to talk to their partners about a plan, and then have them share. Ask them to make conjectures about what degree in Fahrenheit corresponds to 1°C, and have them explain their rationale for the numbers they chose. Consider recording the information, and have the class vote on which answer they think is closest to correct.
→ We need to divide the Celsius number line from 0 to 100 into 100 equal parts. The first division to the right of zero will be the location of 1°C.

Now that we know where to locate 1°C on the lower number line, we need to figure out what number it corresponds to on the upper number line representing Fahrenheit. Like we did with Celsius, we divide the number line from 32 to 212 into 100 equal parts. The number line from 32 to 212 is actually a length of 180 units (212 – 32 = 180). Now, how would we determine the precise number in Fahrenheit that corresponds to 1°C?
Provide students time to talk to their partners and compute the answer.
→ We need to take the length 180 and divide it into 100 equal parts.
\(\frac{180}{100}\) = \(\frac{9}{5}\) = 1 \(\frac{4}{5}\) = 1.8
→ If we look at a magnified version of the number line with this division, we have the following diagram:

→ Based on your computation, what number falls at the intersection of the Fahrenheit number line and the red line that corresponds to 1°C? Explain.
Since we know that each division on the Fahrenheit number line has a length of 1.8, then when we start from 32 and add 1.8, we get 33.8. Therefore, 1°C is equal to 33.8°F.

Revisit the conjecture made at the beginning of the activity, and note which student came closest to guessing 33.8°F. Ask the student to explain how he arrived at such a close answer.

→ Eventually, we want to revisit the original two questions. But first, let’s look at a few more concrete questions. What is 37°C in Fahrenheit? Explain.
Provide students time to talk to their partners about how to answer the question. Ask students to share their ideas and explain their thinking.
→ Since the unit length on the Celsius scale is equal to the unit length on the Fahrenheit scale, then 37°C means we need to multiply (37 × 1.8) to determine the corresponding location on the Fahrenheit scale. But, because 0 on the Celsius scale is 32 on the Fahrenheit scale, we will need to add 32 to our answer. In other words, 37°C = (32 + 37 × 1.8)°F = (32 + 66.6)°F = 98.6°F.

Exercises
Determine the corresponding Fahrenheit temperature for the given Celsius temperatures in Exercises 1–5.

Exercise 1.
How many degrees Fahrenheit is 25°C?
Answer:
25°C = (32 + 25 × 1.8)°F = (32 + 45)°F = 77°F

Exercise 2.
How many degrees Fahrenheit is 42°C?
Answer:
42°C = (32 + 42 × 1.8)°F = (32 + 75.6)°F = 107.6°F

Exercise 3.
How many degrees Fahrenheit is 94°C?
Answer:
94°C = (32 + 94 × 1.8)°F = (32 + 169.2)°F = 201.2°F

Exercise 4.
How many degrees Fahrenheit is 63°C?
Answer:
63°C = (32 + 63 × 1.8)°F = (32 + 113.4)°F = 145.4°F

Exercise 5.
How many degrees Fahrenheit is t°C?
Answer:
t°C = (32 + 1.8t)°F

Eureka Math Grade 8 Module 4 Lesson 30 Problem Set Answer Key

Question 1.
Does the equation t°C = (32 + 1.8t)°F work for any rational number t? Check that it does with t = 8 \(\frac{2}{3}\) and t = – 8 \(\frac{2}{3}\).
Answer:
(8 \(\frac{2}{3}\))°C = (32 + 8 \(\frac{2}{3}\) × 1.8)°F = (32 + 15.6)°F = 47.6°F
( – 8 \(\frac{2}{3}\))°C = (32 + ( – 8 \(\frac{2}{3}\)) × 1.8)°F = (32 – 15.6)°F = 16.4°F

Question 2.
Knowing that t°C = (32 + \(\frac{9}{5}\) t)°F for any rational t, show that for any rational number d, d°F = (\(\frac{5}{9}\) (d – 32))°C.
Answer:
Since d°F can be found by (32 + \(\frac{9}{5}\) t), then d = (32 + \(\frac{9}{5}\) t), and d°F = t°C. Substituting d = (32 + \(\frac{9}{5}\) t) into d°F, we get
d°F = (32 + \(\frac{9}{5}\) t)°F
d = 32 + \(\frac{9}{5}\) t
d – 32 = \(\frac{9}{5}\) t
\(\frac{5}{9}\) (d – 32) = t.
Now that we know t = \(\frac{5}{9}\) (d – 32), then d°F = (\(\frac{5}{9}\) (d – 32))°C.

Question 3.
Drake was trying to write an equation to help him predict the cost of his monthly phone bill. He is charged $35 just for having a phone, and his only additional expense comes from the number of texts that he sends. He is charged $0.05 for each text. Help Drake out by completing parts (a)–(f).
a. How much was his phone bill in July when he sent 750 texts?
Answer:
35 + 750(0.05) = 35 + 37.5 = 72.5
His bill in July was $72.50.

b. How much was his phone bill in August when he sent 823 texts?
Answer:
35 + 823(0.05) = 35 + 41.15 = 76.15
His bill in August was $76.15.

c. How much was his phone bill in September when he sent 579 texts?
Answer:
35 + 579(0.05) = 35 + 28.95 = 63.95
His bill in September was $63.95.

d. Let y represent the total cost of Drake’s phone bill. Write an equation that represents the total cost of his phone bill in October if he sends t texts.
Answer:
y = 35 + t(0.05)

e. Another phone plan charges $20 for having a phone and $0.10 per text. Let y represent the total cost of the phone bill for sending t texts. Write an equation to represent his total bill.
Answer:
y = 20 + t(0.10)

f. Write your equations in parts (d) and (e) as a system of linear equations, and solve. Interpret the meaning of the solution in terms of the phone bill.
Answer:
(y = 35 + t(0.05)
y = 20 + t(0.10)
35 + (0.05)t = 20 + (0.10)t
15 + (0.05)t = (0.10)t
15 = 0.05t
300 = t
y = 20 + 300(0.10)
y = 50
The solution is (300,50), meaning that when Drake sends 300 texts, the cost of his bill will be $50 using his current phone plan or the new one.

Eureka Math Grade 8 Module 4 Lesson 30 Exit Ticket Answer Key

Use the equation developed in class to answer the following questions:
Question 1.
How many degrees Fahrenheit is 11°C?
Answer:
11°C = (32 + 11 × 1.8)°F
11°C = (32 + 19.8)°F
11°C = 51.8°F

Question 2.
How many degrees Fahrenheit is – 3°C?
Answer:
– 3°C = (32 + ( – 3) × 1.8)°F
– 3°C = (32 – 5.4)°F
– 3°C = 26.6°F

Question 3.
Graph the equation developed in class, and use it to confirm your results from Problems 1 and 2.

Answer:

When I graph the equation developed in class, t°C = (32 + 1.8t)°F, the results from Problems 1 and 2 are on the line, confirming they are solutions to the equation.

Engage NY Eureka Math Kindergarten Module 3 Lesson 10 Answer Key

Eureka Math Kindergarten Module 3 Lesson 10 Homework Answer Key

Question 1.

The golf ball is as heavy as _______ pennies.
Answer:
The golf ball is as heavy as 6 pennies.

Explanation:
In the above picture in the left side of the balance their is a golfball and in the right side of the balance there are 6 pennies.The balance shows equal weight on both sides.Therefore, 1 golfball is as heavy as 6 pennies.

Question 2.

The toy train is as heavy as _______ pennies.
Answer:
The toy train is as heavy as 9 pennies.

Explanation:
In the above picture in the left side of the balance their is a Toytrain and in the right side of the balance there are 9 pennies.The balance shows equal weight on both sides.Therefore, 1 toytrain is as heavy as 9 pennies.

Question 3.

Draw in the pennies so the carrot is as heavy as 5 pennies.
Answer:

Explanation:
In the above picture i drew 5 pennies as given that the carrot is as heavy as 5 pennies.

Question 4.

Draw in the pennies so the book is as heavy as 10 pennies.
Answer:

Explanation:
In the above picture i drew 10 pennies as given that the book is as heavy as 10 pennies.

Engage NY Eureka Math Kindergarten Module 3 Lesson 9 Answer Key

Eureka Math Kindergarten Module 3 Lesson 9 Homework Answer Key

Draw something inside the box that is heavier than the object on the balance.

Question 1.

Answer:

Explanation:
A bunch of flowers is heavier than a feather.So, i drew a bunch of flowers in the box.

Question 2.

Answer:

Explanation:
A watermelon is heavier than an apple.So, i drew a watermelon in the box.

Draw something lighter than the object on the balance.

Question 1.

Answer:

Explanation:
A balloon is lighter than a ball.So, i drew a balloon in the box.

Question 2.

Answer:

Explanation:
A tomato is lighter than a pumpkin.So, i drew a tomato in the box.

Engage NY Eureka Math Kindergarten Module 3 Lesson 8 Answer Key

Eureka Math Kindergarten Module 3 Lesson 8 Problem Set Answer Key

Which is heavier? Circle the object that is heavier than the other.

Question 1.

Answer:

Explanation:
I circled book because it is heavier than a scissors.

Question 2.

Answer:

Explanation:
I circled pen because it is heavier than a paper.

Question 3.

Answer:

Explanation:
I circled bear because it is heavier than a teddybear.

Question 4.

Answer:

Explanation:
I circled shoe because it is heavier than a socks.

Question 5.

Answer:

Explanation:
I circled ball because it is heavier than a balloon.

Question 6.

Answer:

Explanation:
I circled watermelon because it is heavier than an apple.

Eureka Math Kindergarten Module 3 Lesson 8 Homework Answer Key

Draw an object that would be lighter than the one in the picture.

Question 1.

Answer:

Explanation:
A balloon will be lighter than a ball.So, i drew a balloon.

Question 2.

Answer:

Explanation:
An orange will be lighter than a pineapple.So, i drew an orange.

Question 3.

Answer:

Explanation:
A chair will be lighter than a table.So, i drew a chair.

Question 4.

Answer:

Explanation:
A book will be lighter than a bag.So, i drew a book.

Engage NY Eureka Math Kindergarten Module 3 Lesson 7 Answer Key

Eureka Math Kindergarten Module 3 Lesson 7 Problem Set Answer Key

These boxes represent cubes.

Question 1.

Answer:

Explanation:
I colored 2 cubes red and 3 cubes green.There are 5 color cubes.

Question 2.

Answer:

Explanation:
I colored 1 cube red and 4 cubes green.There are 5 color cubes.

Question 1.
Trace a 6-stick. Find something the same length as your 6-stick.
Draw a picture of it here.
Answer:

Explanation:
I drew a 6-stick and drew a chalkpiece which is same length as 6-stick.

Question 2.
Trace a 7-stick. Find something the same length as your 7-stick.
Draw a picture of it here.
Answer:

Explanation:
I drew a 7-stick and drew a cflowervase which is same length as 7-stick.

Question 3.
Trace an 8-stick. Find something the same length as your 8-stick.
Draw a picture of it here.
Answer:

Explanation:
I drew a 8-stick and drew a marker which is same length as 8-stick.

Eureka Math Kindergarten Module 3 Lesson 7 Homework Answer Key

These boxes represent cubes.

Question 1.

Color 2 cubes green. Color 3 cubes blue.
Together, my green 2-stick and blue 3-stick are the same length as 5 cubes.
Answer:

Explanation:
I colored 2 cubes green, 3 cubes blue.
Together, my green 2-stick and blue 3-stick are the same length as 5 cubes.

Question 2.

Color 3 cubes blue. Color 2 cubes green.
Together, my blue 3-stick and green 2-stick are the same length as ___ cubes.
Answer:

Explanation:
I colored 3 cubes blue and 2 cubes green.
Together, my blue 3-stick and green 2-stick are the same length as 5 cubes.

Question 3.

Color 1 cube green. Color 4 cubes blue.
How many did you color? ________
Answer:

Explanation:
I colored 1 cube green and 4 cubes blue.
Altogether i colored 5 cubes.

Question 4.

Color 4 cubes green. Color 1 cube blue.
How many did you color? ________
Answer:

Explanation:
I colored 4 cubes green and 1 cube blue.
Altogether i colored 5 cubes.

Question 5.

Color 2 cubes yellow. Color 2 cubes blue.
Together, my 2 yellow and 2 blue are the same as _____.
Answer:

Explanation:
I colored 2 cubes yellow, 2 cubes blue.
Together, my 2 yellow and 2 blue are the same as 4 cubes.

Engage NY Eureka Math Kindergarten Module 3 Lesson 6 Answer Key

Eureka Math Kindergarten Module 3 Lesson 6 Problem Set Answer Key

In the box, write the number of cubes there are in the pictured stick. Draw a green circle around the stick if it is longer than the object. Draw a blue circle around the stick if it is shorter than the object.

Question 1.

Answer:

Explanation:
There are 6 cubes in the above cube.I circled the cube with blue as the stick is shorter tahn the object.

Question 2.

Answer:

Explanation:
There are 9 cubes in the above stick.I circled it green as the stick is longer than the object.

Question 1.
Make a 3-stick. In your classroom, select a crayon, and see if your crayon is longer than or shorter than your stick.
Trace your 3-stick and your crayon to compare their lengths.
Answer:

Explanation:
I drew a 3-stick and a crayon.I traced them to compare the lengths.The crayon is longer than the 3-stick.

Question 2.
In your classroom, find a marker, and make a stick that is longer than your marker.
Trace your stick and your marker to compare their lengths.
Answer:

Explanation:
I drew a marker and a stick longer than the marker.I traced them to comapre their lengths.The stick is longer than the marker.

Question 3.
Make a 5-stick. Find something in the classroom that is longer than your 5-stick.
Trace your 5-stick and the object to compare their lengths.
Answer:

Explanation:
I drew a 5-stick and a chair from my classroom.I traced them to compare their lengths.The chair is longer than the 5-stick.

Eureka Math Kindergarten Module 3 Lesson 6 Homework Answer Key

Color the cubes to show the length of the object.

Question 1.

Answer:

Explanation:
I colored the stick upto 7cubes as the object is 7-stick long.

Question 2.

Answer:

Explanation:
I colored the stick upto 4 cubes as the object is 4-stick long.

Question 3.

Answer:

Explanation:
I colored the stick upto 3 cubes as the object is 3-stick long.

Question 4.

Answer:

Explanation:
I colored the ctick upto 4 cubes as the object is 4-stick long.

Engage NY Eureka Math Kindergarten Module 3 Lesson 5 Answer Key

Eureka Math Kindergarten Module 3 Lesson 5 Problem Set Answer Key

Circle the stick that is shorter than the other.

Question 1.

Answer:

Explanation:
I circled the  shorter stick in the above picture.

Question 2.

Answer:

Explanation:
I circled the shorter stick in the above picture.

Circle the stick that is longer than the other.

Answer:

Explanation:
I circled the longer stick in the above picture.

My _____ -stick is longer than my _____ -stick.
Answer:
My 5 -stick is longer than my 4 -stick.

My _____ -stick is shorter than my ____ -stick.
Answer:
My 4-stick is shorter than my 5-stick.

Circle the stick that is shorter than the other stick.

Answer:

Explanation:
I circled the shorter stick in the above picture.

My _____ -stick is longer than my _____ -stick.
Answer:
My 9-stick is longer than my 7-stick.

My _____ -stick is shorter than my _____ -stick.
Answer:
My 7-stick is shorter than my  9-stick.

Eureka Math Kindergarten Module 3 Lesson 5 Homework Answer Key

Circle the stick that is shorter than the other.

Answer:

Explanation:
I circled the shorter stick in the above picture.

My _____ -stick is shorter than my _____ -stick.
Answer:
My 8-stick is shorter than my 9-stick.

My _____ -stick is longer than my _____ -stick.
Answer:
My 9-stick is longer than my 8-stick.

Engage NY Eureka Math Kindergarten Module 3 Lesson 3 Answer Key

Eureka Math Kindergarten Module 3 Lesson 3 Homework Answer Key

Take out a new crayon. Circle objects with lengths shorter than the crayon blue. Circle objects with lengths longer than the crayon red.

Answer:

Explanation:
I circled the cars with red that are longer than a cayon and circled the cars with blue that are shorter than a crayon.

On the back of your paper, draw some things shorter than the crayon and longer than the crayon. Draw something that is the same length as the crayon.
Answer:

Explanation:
An eraser is shorter than a crayon, pencil is longer than a crayon and key is same length of crayon.

Engage NY Eureka Math Kindergarten Module 3 Lesson 4 Answer Key

Eureka Math Kindergarten Module 3 Lesson 4 Problem Set Answer Key

Circle the shorter stick.

Question 1.

How many linking cubes are in the shorter stick? Write the number in the box.
Answer:

Explanation:
I circled the shorter stick and it has 4 cubes in it.

Question 2.

How many linking cubes are in the shorter stick? Write the number in the box.
Answer:

Explanation:
I circled the shorter stick and it has 3 cubes in it.

Circle the longer stick.

Question 1.

How many linking cubes are in the longer stick? Write the number in the box.
Answer:

Explanation:
I circled the longer stick and it has 6 cubes in it.

Question 2.

How many linking cubes are in the longer stick? Write the number in the box.
Answer:

Explanation:
I circled the longer stick and it has 7 cubes in it.

Draw a stick shorter than my 5-stick.

Answer:

Explanation:
I drew a 4 cube stick which is shorter than the 5 cube stick that is given in the above picture.

Draw a stick longer than mine.

Answer:

Explanation:
I drew a 8 cube stick which is longer than the stick given in the above picture.

Draw a stick shorter than mine.

Answer:

Explanation:
I drew a 5 cube stick which is shorter than the stick given in the picture.

Eureka Math Kindergarten Module 3 Lesson 4 Homework Answer Key

Use a red crayon to circle the sticks that are shorter than the 5-stick.

Answer:

Explanation:
I circled the sticks that are shorter than the 5-stick with a red crayon.

Use a blue crayon to circle the sticks that are longer than the 5-stick.

Answer:

Explanation:
I circled the sticks that are longer than the 5-stick with a blue crayon.