Prasanna – Page 67 – Big Ideas Math Answers

Eureka Math Grade 3 Module 2 Lesson 11 Answer Key

April 1, 2022March 23, 2021 by Prasanna

Engage NY Eureka Math 3rd Grade Module 2 Lesson 11 Answer Key

Eureka Math Grade 3 Module 2 Lesson 11 Problem Set Answer Key

Question 1.
The total weight in grams of a can of tomatoes and a jar of baby food is shown to the right.
a. The jar of baby food weighs 113 grams. How much does the can of tomatoes weigh?
$Eureka Math Grade 3 Module 2 Lesson 11 Problem Set Answer Key 1$

Answer:

Explanation:
The total weight in grams of a can of tomatoes and a jar of baby food is 671g and 113g.To find the weight of the can of tomatoes, subtract 113 from 671.
671-113=558g.
The weight of the can of tomatoes is 558g.

b. How much more does the can of tomatoes weigh than the jar of baby food?

Answer:

Explanation:
The weight of the can of tomatoes is 558g.
A jar of baby food is 113g
So, subtract 113 from 558
558-113=445
Therefore, 445g more does can of tomatoes weigh than the jar of baby food.

Question 2.
The weight of a pen in grams is shown to the right.
a. What is the total weight of 10 pens?

Answer:
As shown in the picture the weight of pen is 6g.
If 1 pen is 6 grams then the weight of 10 pens is 6 x 10=60g
Therefore the total weight of 10 pens is 60grams.

b. An empty box weighs 82 grams. What is the total weight of a box of 10 pens?
$Eureka Math Grade 3 Module 2 Lesson 11 Problem Set Answer Key 1.1$

Answer:

Explanation:
As we know from the above sum the weight of 10 pens is 60g and an empty box weighs 82 grams then the total weight will be 60+82=142grams.

Question 3.
The total weight of an apple, lemon, and banana in grams is shown to the right.
a. If the apple and lemon together weigh 317 grams, what is the weight of the banana?
$Eureka Math Grade 3 Module 2 Lesson 11 Problem Set Answer Key 2$

Answer:

Explanation:
The total weight of an apple, lemon, and banana in grams is 508g and the apple and lemon together weigh 317 grams.
The weight of the banana is 508-317g=191g
Therefore, the weight of the banana is 191grams.

b. If we know the lemon weighs 68 grams less than the banana, how much does the lemon weigh?

Answer:

Explanation:
The weight of the banana is 191grams
If we know the lemon weighs 68 grams less than the banana, then the weight of lemon will be 191-68=123g
Therefore, the lemon weighs 123g.

c. What is the weight of the apple?

Answer:

Explanation:
If the apple and lemon together weigh 317 grams, the lemon weighs 123g then the weight of only apple will be 317-123=194g
Therefore, the weight of the apple is 194grams.

Question 4.
A frozen turkey weighs about 5 kilograms. The chef orders 45 kilograms of turkey. Use a tape diagram to find about how many frozen turkeys he orders.

Answer:

Explanation:
A frozen turkey weighs about 5 kilograms, the chef orders 45 kilograms of turkey.
If each turkey weighs 5 grams then divide 45 by 5.
45/5=9
Therefore, 9 frozen turkeys the chef orders.

Question 5.
A recipe requires 300 milliliters of milk. Sara decides to triple the recipe for dinner. How many milliliters of milk does she need to cook dinner?

Answer:

Explanation:
A recipe requires 300 milliliters of milk.If Sara decides to triple the recipe for dinner add 300ml+300ml+300ml=900ml
Therefore, 900milliliters of milk does she need to cook dinner.

Question 6.
Marian pours a full container of water equally into buckets. Each bucket has a capacity of 4 liters. After filling 3 buckets, she still has 2 liters left in her container. What is the capacity of her container?

Answer:

Explanation:
Marian pours a full container of water equally into buckets.If each bucket has a capacity of 4 liters and after filling 3 buckets, if she still has 2 liters left in her container then multiply 4L with 3 buckets
4 x 3=12.
Then add the 2L of water left to 12L
12+2=14L
Therefore, the capacity of her container is 14Liters.

Eureka Math Grade 3 Module 2 Lesson 11 Exit Ticket Answer Key

The capacities of three cups are shown below.
$Engage NY Math 3rd Grade Module 2 Lesson 11 Exit Ticket Answer Key 3$
a. Find the total capacity of the three cups.

Answer:

Explanation:
The capacities of three cups are Cup A 160ml, Cup B 280ml and Cup C 237ml
To find the total capacity of the three cups add 160+280+237=677ml
Therefore, the total capacity of the three cups is 677ml.

b. Bill drinks exactly half of Cup B. How many milliliters are left in Cup B?

Answer:
The capacity of Cup B is 280ml, if Bill drinks exactly half of Cup B then the drink left in the cup is half.
280/2=140
Therefore, 140 milliliters are left in Cup B.

c. Anna drinks 3 cups of tea from Cup A. How much tea does she drink in total?

Answer:

Explanation:
Anna drinks 3 cups of tea from Cup A.
Add 160+160+160=480ml
Therefore, 480ml of tea Anna drinks in total.

Eureka Math Grade 3 Module 2 Lesson 11 Homework Answer Key

Question 1.
Karina goes on a hike. She brings a notebook, a pencil, and a camera. The weight of each item is shown in the chart. What is the total weight of all three items?

Item	Weight
Notebook	312 g
Pencil	10 g
Camera	365 g

The total weight is __________ grams.

Answer:

Explanation:
Karina goes on a hike. She brings a notebook, a pencil, and a camera.
The weight of notebook is 312g, pencil is 10g and camera is 365g.
Add 312+10+365=687g
Therefore, the total weight of all three items is 687grams.

Question 2.
Together a horse and its rider weigh 729 kilograms. The horse weighs 625 kilograms. How much does the rider weigh?
The rider weighs __________ kilograms.

Answer:

Explanation:
Together a horse and its rider weigh 729 kilograms. The horse weighs 625 kilograms.
Subtract the weight of horse from the total to find the weight of the rider
729-625=104
Therefore, The rider weighs 104 kilograms

Question 3.
Theresa’s soccer team fills up 6 water coolers before the game. Each water cooler holds 9 liters of water. How many liters of water do they fill?

Answer:

Explanation:
Theresa’s soccer team fills up 6 water coolers before the game. Each water cooler holds 9 liters of water
If each cooler holds 9L and soccer team fills 6 colers, to find the total number of liters of water the filled,
multiply 9 by 6=9 x 6=54
Therefore, liters of water they filled is 54.

Question 4.
Dwight purchased 48 kilograms of fertilizer for his vegetable garden. He needs 6 kilograms of fertilizer for each bed of vegetables. How many beds of vegetables can he fertilize?

Answer:

Explanation:
Dwight purchased 48 kilograms of fertilizer for his vegetable garden.
If he needs 6 kilograms of fertilizer for each bed of vegetables,
To find the number beds of vegetables he can fertilize divide 48 by 6
48/6=8
Therefore, 8 beds of vegetables he can fertilize.

Question 5.
Nancy bakes 7 cakes for the school bake sale. Each cake requires 5 milliliters of oil. How many milliliters of oil does she use?

Answer:

Explanation:
Nancy bakes 7 cakes for the school bake sale. Each cake requires 5 milliliters of oil
To find the number of milliliters of oil she used multiply 7 with 5
7 x 5 =35
Therefore, 35milliliters of oil she used to bake 7 cakes.

Eureka Math Grade 3 Module 2 Answer Key

Eureka Math Grade 3 Module 2 Lesson 10 Answer Key

April 1, 2022March 23, 2021 by Prasanna

Engage NY Eureka Math 3rd Grade Module 2 Lesson 10 Answer Key

Eureka Math Grade 3 Module 2 Lesson 10 Problem Set Answer Key

Question 1.
Label the vertical number line on the container to the right. Answer the questions below.
a. What did you label as the halfway mark? Why?
$Eureka Math Grade 3 Module 2 Lesson 10 Problem Set Answer Key 1$

Answer:
500ml is the halfway mark because i made 10 marksand 10/2=5.So, the 5th mark is the halfway mark.

b. Explain how pouring each plastic cup of water helped you create a vertical number line.

Answer:
As i poured same amount of water each time that is 100ml for ten times it helped me to create a vertical number line.

c. If you pour out 300 mL of water, how many mL are left in the container?

Answer:
700ml

Explanation:
There are total 1000ml of water in the container, if we pour out 300ml of water from the container 700ml will be left.
100-300=700ml.

Question 2.
How much liquid is in each container?
$Eureka Math Grade 3 Module 2 Lesson 10 Problem Set Answer Key 2$

Answer:

Question 3.
Estimate the amount of liquid in each container to the nearest hundred milliliters.
$Eureka Math Grade 3 Module 2 Lesson 10 Problem Set Answer Key 3$

Answer:

Question 4.
The chart below shows the capacity of 4 barrels.

Barrel A	75 liters
Barrel B	68 liters
Barrel C	96 liters
Barrel D	52 liters

a. Label the number line to show the capacity of each barrel. Barrel A has been done for you.
b. Which barrel has the greatest capacity?

Answer:
Barrel A

c. Which barrel has the smallest capacity?

Answer:
Barrel D

d. Ben buys a barrel that holds about 70 liters. Which barrel did he most likely buy? Explain why.

Answer:
Barrel A

Explanation:
If Ben buys a barrel that holds 70liters he need to buy most likely Barrel A because its capacity is 75 liters and only barrel A can hold 70liters compared with the other barrels.

e. Use the number line to find how many more liters Barrel C can hold than Barrel B.

Answer:
28 liters

Explanation:
Barrel C contains 96 liters and barrel B 68 liters.The difference is 96-68=28 liters.

$Eureka Math Grade 3 Module 2 Lesson 10 Problem Set Answer Key 4$

Eureka Math Grade 3 Module 2 Lesson 10 Exit Ticket Answer Key

Question 1.
Use the number line to record the capacity of the containers.

Container	Capacity in Liters
A	57 liters
B	45 liters
C	21 liters

$Engage NY Math 3rd Grade Module 2 Lesson 10 Exit Ticket Answer Key 5$

Question 2.
What is the difference between the capacity of Container A and Container C?

Answer:
36

Explanation:
Container A has 57 liters and Container C has 21 liters.Difference between the capacity of Container A and Container C is 57-21=36 liters.

Eureka Math Grade 3 Module 2 Lesson 10 Homework Answer Key

Question 1.
How much liquid is in each container?
$Eureka Math 3rd Grade Module 2 Lesson 10 Homework Answer Key 6$

Answer:

Question 2.
Jon pours the contents of Container 1 and Container 3 above into an empty bucket. How much liquid is in the bucket after he pours the liquid?

Answer:
11 liters

Explanation:
Container 1 contains 5 liters and container 3 has 6 liters.If Jon pours the contents of Container 1 and Container 3 into an empty bucket it holds 5+6=11liters in it.

Question 3.
Estimate the amount of liquid in each container to the nearest liter.
$Eureka Math 3rd Grade Module 2 Lesson 10 Homework Answer Key 7$

Answer:

Question 4.
Kristen is comparing the capacity of gas tanks in different size cars. Use the chart below to answer the questions.

Size of Car	Capacity in Liters
Large	74
Medium	57
Small	42

a. Label the number line to show the capacity of each gas tank. The medium car has been done for you.
$Eureka Math 3rd Grade Module 2 Lesson 10 Homework Answer Key 8$
b. Which car’s gas tank has the greatest capacity?

Answer:
Large car with 74liters of gas.

c. Which car’s gas tank has the smallest capacity?

Answer:
Small car with 42 liters of gas.

d. Kristen’s car has a gas tank capacity of about 60 liters. Which car from the chart has about the same capacity as Kristen’s car?

Answer:
Medium car

Explanation:
Kristen’s car has a gas tank capacity of about 60 liters.As the capacity of the medium car is 57 liters,medium car from the chart has about the same capacity as Kristen’s car.

e. Use the number line to find how many more liters the large car’s tank holds than the small car’s tank.

Answer:
32

Explanation:
The capacity of gas tank of large car is 74 an dthe small car is 42.the difference is 74-42=32.

Eureka Math Grade 3 Module 2 Answer Key

Eureka Math Grade 3 Module 2 Lesson 9 Answer Key

April 1, 2022March 23, 2021 by Prasanna

Engage NY Eureka Math 3rd Grade Module 2 Lesson 9 Answer Key

Eureka Math Grade 3 Module 2 Lesson 9 Problem Set Answer Key

Part 1
a.
Predict whether each container holds less than, more than, or about the same as 1 liter.
$Eureka Math Grade 3 Module 2 Lesson 9 Problem Set Answer Key 1$

b. After measuring, what surprised you? Why?

Part 2

c. Illustrate and describe the process of decomposing 1 liter of water into 10 smaller units.

Answer:

Explanation:
I decomposed 1liter of water into 10 smaller units by pouring 100 milliliter of water into each cup.Then count each cup by 100ml.I found that 1000ml that is 10 groups of 100ml is equal to 1 liter.
1000ml/10=100ml.

d. Illustrate and describe the process of decomposing Cup K into 10 smaller units.

Answer:

Explanation:
I decomposed 100ml of water into 10 smaller units by pouring 10milliliter of water into each cup.Then count each cup by 10ml.I found that 100ml that is 10 groups of 10ml is equal to 100ml.
100ml/10=10ml

e. Illustrate and describe the process of decomposing Cup L into 10 smaller units.

Answer:

Explanation:
I decomposed 10ml of water into 10 smaller units by pouring 1milliliter of water into each cup.Then count each cup by 1ml.I found that 10ml that is 10 groups of 1ml is equal to 1ml.
10ml/10=1ml

f. What is the same about decomposing 1 liter into milliliters and decomposing 1 kilogram into grams?

Answer:
Decomposing of 1 liter into milliliters and decomposing 1 kilogram into grams will work same.10ml is ten 1ml, 100ml is ten 10ml and 1 liter is ten 100ml.Both kilograms and grams and liters and milliters are same.

g. One liter of water weighs 1 kilogram. How much does 1 milliliter of water weigh? Explain how you know.

Answer:
Since decomposing 1 liter into milliters is same as decomposing 1 kilogram into grams, we know that 1ml weighs same as 1 gram.

Eureka Math Grade 3 Module 2 Lesson 9 Exit Ticket Answer Key

Question 1.
Morgan fills a 1-liter jar with water from the pond. She uses a 100-milliliter cup to scoop water out of the pond and pour it into the jar. How many times will Morgan scoop water from the pond to fill the jar?

Answer:
10 times

Explanation:
Morgan fills a 1-liter jar with water from the pond. She uses a 100-milliliter cup to scoop water out of the pond and pour it into the jar
As we know 1l is ten 100ml
To find the number of times Morgan scoop water from the pond to fill the jar morgan has to pour 10 times.

Question 2.
How many groups of 10 milliliters are in 1 liter? Explain.
There are _____________ groups of 10 milliliters in 1 liter.

Answer:
There are 100 groups of 10 milliliters in 1 liter.

Explanation:
As we know 1l is equal to ten 100ml and 100ml is equal to ten 10ml.Therefore 1l is equal to hundred 10ml.
Therefore, There are 100 groups of 10 milliliters in 1 liter.

Eureka Math Grade 3 Module 2 Lesson 9 Homework Answer Key

Question 1.
Find containers at home that have a capacity of about 1 liter. Use the labels on containers to help you identify them.
a.

Name of Container

Example: Carton of orange juice

A water bottle

A tin of oil

A pack of milk

A pack of curd

b. Sketch the containers. How do their sizes and shapes compare?

Question 2.
The doctor prescribes Mrs. Larson 5 milliliters of medicine each day for 3 days. How many milliliters of medicine will she take altogether?

Answer:
The doctor prescribes Mrs. Larson 5 milliliters of medicine each day for 3 days
To find the number of milliliters medicine will she take altogether multiply 5 by 3
5 x 3=15milliliters
Therefore, 15milliliters medicine will she take altogether.

Question 3.
Mrs. Goldstein pours 3 juice boxes into a bowl to make punch. Each juice box holds 236 milliliters. How much juice does Mrs. Goldstein pour into the bowl?

Answer:
Mrs. Goldstein pours 3 juice boxes into a bowl to make punch. Each juice box holds 236 milliliters.
To find the number of milliliters of juice Mrs. Goldstein pour into the bowl multiply 236 by 3
236 x 3=708
Therefore, 708milliliters of juice Mrs. Goldstein pour into the bowl.

Question 4.
Daniel’s fish tank holds 24 liters of water. He uses a 4-liter bucket to fill the tank. How many buckets of water are needed to fill the tank?

Answer:
Daniel’s fish tank holds 24 liters of water. He uses a 4-liter bucket to fill the tank
To find the number of buckets of water needed to fill the tank divide 24 with 4
24/4=6
Therefore, 6 buckets of water are needed to fill the tank.

Question 5.
Sheila buys 15 liters of paint to paint her house. She pours the paint equally into 3 buckets. How many liters of paint are in each bucket?

Answer:
Sheila buys 15 liters of paint to paint her house.She pours the paint equally into 3 buckets.
To find the number of liters of paint are in each bucket divide 15 with 3
15/3=5
Therefore, 5 liters of paint are in each bucket.

Eureka Math Grade 3 Module 2 Answer Key

Eureka Math Grade 3 Module 2 Lesson 8 Answer Key

April 1, 2022March 23, 2021 by Prasanna

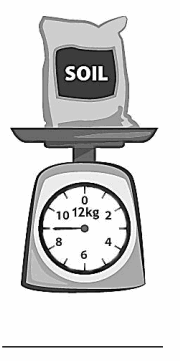
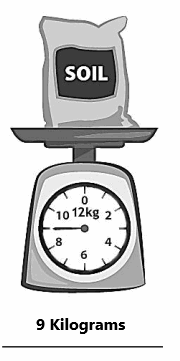
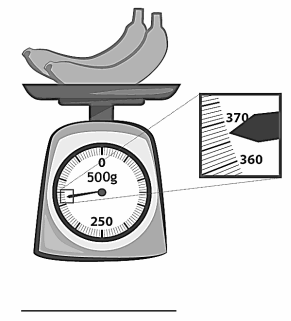
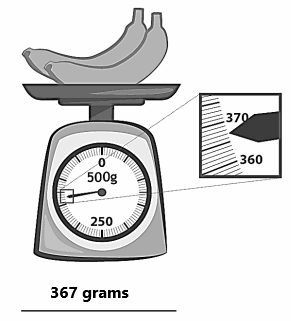
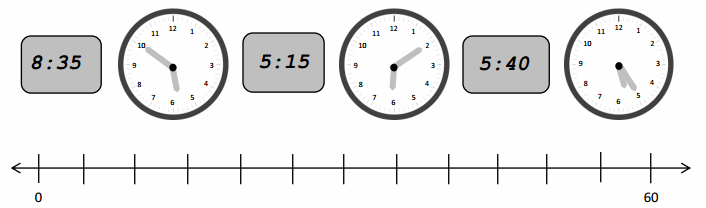
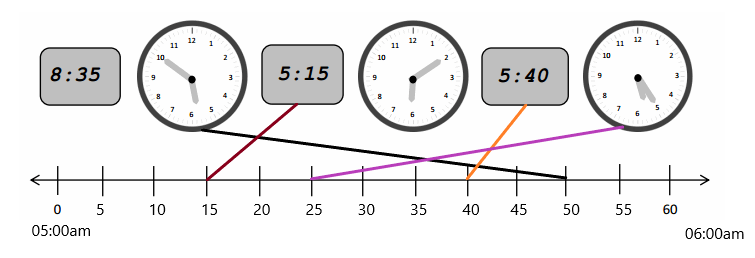
Engage NY Eureka Math 3rd Grade Module 2 Lesson 8 Answer Key

Eureka Math Grade 3 Module 2 Lesson 8 Problem Set Answer Key

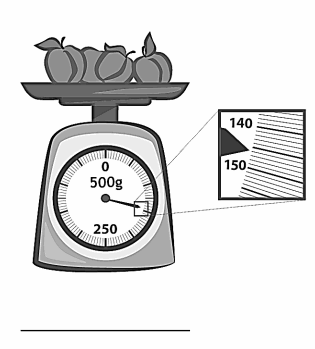
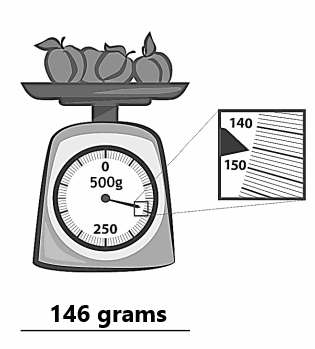
Question 1.
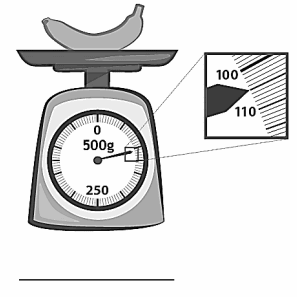
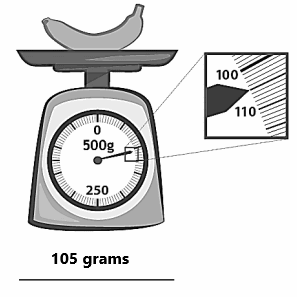
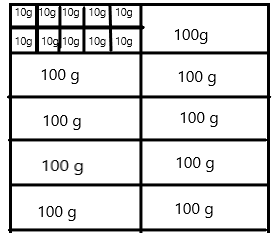
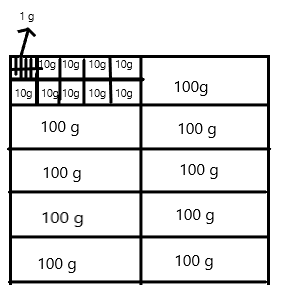
Tim goes to the market to buy fruits and vegetables. He weighs some string beans and some grapes.
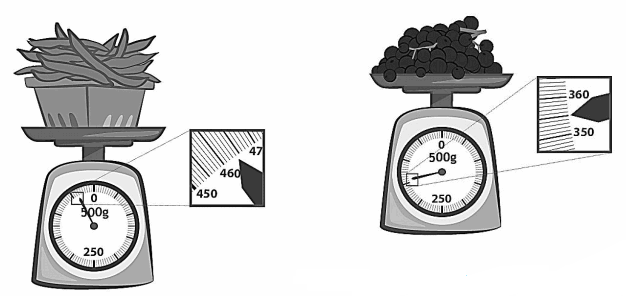
$Eureka Math Grade 3 Module 2 Lesson 8 Problem Set Answer Key 1$
List the weights for both the string beans and grapes.
The string beans weigh _____________ grams.
The grapes weigh _____________ grams.

Answer:
The string beans weigh 464 grams.
The grapes weigh 355 grams.

Question 2.
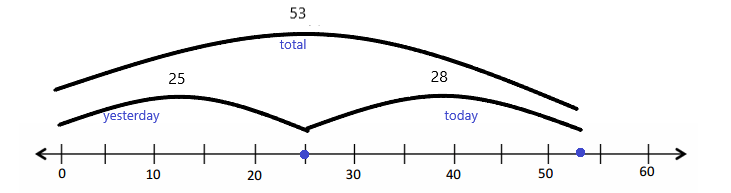
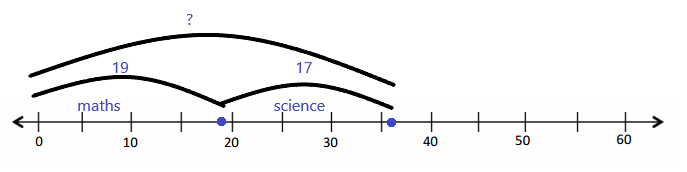
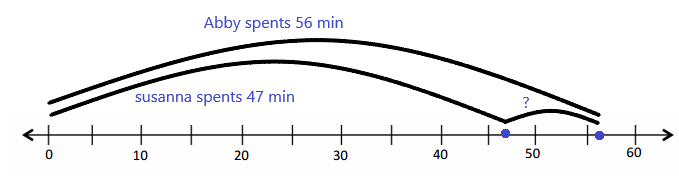
Use tape diagrams to model the following problems. Keiko and her brother Jiro get weighed at the doctor’s office. Keiko weighs 35 kilograms, and Jiro weighs 43 kilograms.
a. What is Keiko and Jiro’s total weight?
Keiko and Jiro weigh __________ kilograms.

Answer:

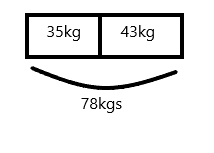
Explanation:
Keiko and her brother Jiro get weighed at the doctor’s office. Keiko weighs 35 kilograms, and Jiro weighs 43 kilograms.
Add 35 and 43
35+43=78kgs
Therefore, Keiko and Jiro weigh 78 kilograms

b. How much heavier is Jiro than Keiko?
Jiro is __________ kilograms heavier than Keiko.

Answer:

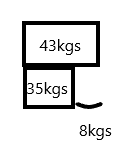
Explanation:
Keiko weighs 35 kilograms, and Jiro weighs 43 kilograms.
Subtract 35 from 43
43-35=8kgs
Therefore, Jiro is 8 kilograms heavier than Keiko

Question 3.
Jared estimates that his houseplant is as heavy as a 5-kilogram bowling ball. Draw a tape diagram to estimate the weight of 3 houseplants.

Answer:

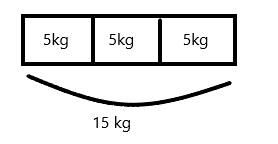
Explanation:
If weight of 1 house plant is 5kg then weight of 3 houseplants will be 5 x 3=15 kg.Therefore the weight of 3houseplants is 15kg.

Question 4.
Jane and her 8 friends go apple picking. They share what they pick equally. The total weight of the apples they pick is shown to the right.
a. About how many kilograms of apples will Jane take home?
$Eureka Math Grade 3 Module 2 Lesson 8 Problem Set Answer Key 2$

Answer:

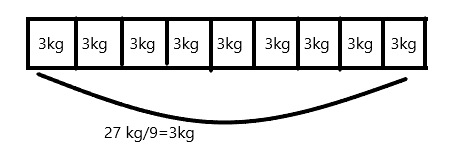
Explanation:
Jane and her 8 friends go apple picking. They share what they pick equally.
There are 27kgs of apples in the weighing balance.
divide 27 kgs of apples with 9 people
27/9=3
Therefore, Jane will take about 3kgs of apples home

b. Jane estimates that a pumpkin weighs about as much as her share of the apples. About how much do 7 pumpkins weigh altogether?

Answer:

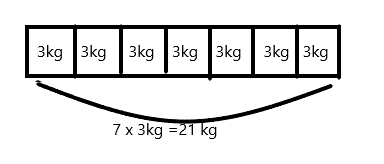
Explanation:
Jane estimates that a pumpkin weighs about as much as her share of the apples.Jane’s share of apples is 3kg.If each pumpkin weighs 3 kgs then the weight of 7 pumpkins will be
7 x 3=21 kg.
Therefore 7 pumpkins weigh 21kgs altogether.

Eureka Math Grade 3 Module 2 Lesson 8 Exit Ticket Answer Key

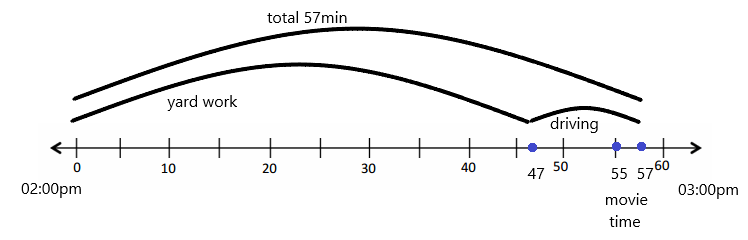
The weights of a backpack and suitcase are shown below.
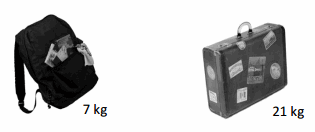
$Engage NY Math 3rd Grade Module 2 Lesson 8 Exit Ticket Answer Key 3$
a. How much heavier is the suitcase than the backpack?

Answer:

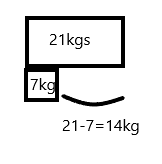
Explanation:
The weight of suitcase is 21 kg but weight of backpack is 7 kg.So, subtract 7 from 21.
21-7=14
Therefore, the suitcase is 14 kg more than the backpack.

b. What is the total weight of 4 identical backpacks?

Answer:

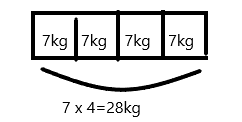
Explanation:
If the weight of each backpack is 7 kgs then the weight of 4 such backpacks will be 7 x 4=28kgs
Therefore, total weight of 4 identical backpacks is 28kgs.

c. How many backpacks weigh the same as one suitcase?

Answer:

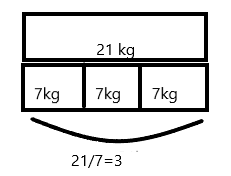
Explanation:
The weight of suitcase is 21 kg and weight of backpack is 7 kg.Divide weight of suitcase and weight of backpack.
21/7=3.
Therefore 3 backpacks weigh the same as one suitcase.

Eureka Math Grade 3 Module 2 Lesson 8 Homework Answer Key

Question 1.
The weights of 3 fruit baskets are shown below.
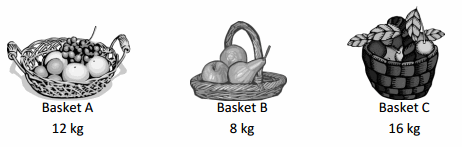
$Eureka Math 3rd Grade Module 2 Lesson 8 Homework Answer Key 4$
a. Basket ______ is the heaviest.

Answer:
Basket C is the heaviest as it has fruits of 16kgs.

b. Basket ______ is the lightest.

Answer:
Basket B is the lightest as it has fruits of 8kgs.

c. Basket A is __________ kilograms heavier than Basket B.

Answer:

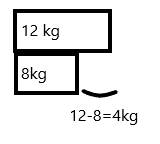
Explanation:
Weight of Basket A is 12kgs and Basket B is 8kgs.Subtract 8 from 12.
12-8=4
Therefore, Basket A is 4 kilograms heavier than Basket B.

d. What is the total weight of all three baskets?

Answer:

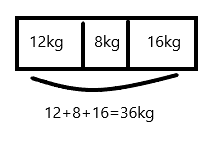
Explanation:
Add the weights of all the 3 baskets
12+8+16=36kgs
Therefore, the total weight of all three baskets is 36kgs.

Question 2.
Each journal weighs about 280 grams. What is total weight of 3 journals?

Answer:

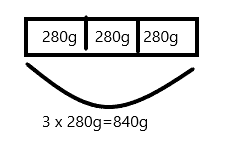
Explanation:
If each journal weighs about 280 grams then total weight of 3 journals will be 3 x 280g=840g
Therefore, weight of 3 journals is 840grams.

Question 3.
Ms. Rios buys 453 grams of strawberries. She has 23 grams left after making smoothies. How many grams of strawberries did she use?

Answer:

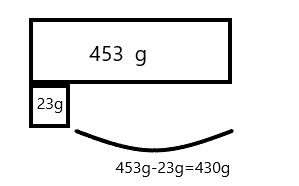
Explanation:
Ms. Rios buys 453 grams of strawberries. She has 23 grams left after making smoothies.Subtract 23g from 453 is 453-23=430
Therefore, Ms. Rios used 430 grams of strawberries.

Question 4.
Andrea’s dad is 57 kilograms heavier than Andrea. Andrea weighs 34 kilograms.
a. How much does Andrea’s dad weigh?

Answer:

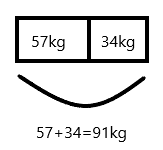
Explanation:
Andrea’s dad is 57 kilograms heavier than Andrea.If Andrea weighs 34 kilograms then her fathers weight is 34+57=91kgs.

b. How much do Andrea and her dad weigh in total?

Answer:

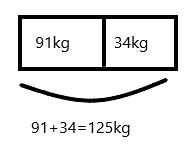
Explanation:
The weight of Andrea is 34kgs and weight of Andreas father is 91kgs.Add 91 and 34
91+34=125kg
Therefore, Andrea and her dad weigh 125kgs in total.

Question 5.
Jennifer’s grandmother buys carrots at the farm stand. She and her 3 grandchildren equally share the carrots. The total weight of the carrots she buys is shown below.
a. How many kilograms of carrots will Jennifer get?
$Eureka Math 3rd Grade Module 2 Lesson 8 Homework Answer Key 5$

Answer:

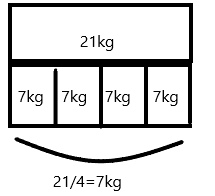
Explanation:
Jennifer’s grandmother buys carrots at the farm stand. She and her 3 grandchildren equally share the carrots.She buys 28kgs of carrots.
Her share of carrots is 28/4=7kgs.
Therefore, jennifer gets 7 kilograms of carrots.

b. Jennifer uses 2 kilograms of carrots to bake muffins. How many kilograms of carrots does she have left?

Answer:

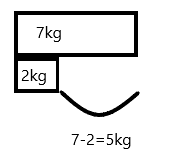
Explanation:
Jennifer gets 7 kilograms of carrots.
If Jennifer uses 2 kilograms of carrots to bake muffins then she will be left with 7-2=5kgs
Therefore, 5 kilograms of carrots she have left.

Eureka Math Grade 3 Module 2 Answer Key

Eureka Math Grade 3 Module 2 Lesson 7 Answer Key

April 1, 2022March 23, 2021 by Prasanna

Engage NY Eureka Math 3rd Grade Module 2 Lesson 7 Answer Key

Eureka Math Grade 3 Module 2 Lesson 7 Problem Set Answer Key

Work with a partner. Use the corresponding weights to estimate the weight of objects in the classroom. Then, check your estimate by weighing on a scale.
A.

Objects that Weigh About 1 Kilogram	Actual Weight
A Water bottle	980g
A Dictionary	1100g
My shoes	1250g

Objects that Weigh About 100 grams	Actual Weight
A Notebook	110g
An Apple	95g
A Pencil box	108g

Objects that Weigh About 10 grams	Actual Weight
An Eraser	8g
A Marker	12g
My Bracelet	9g

Objects that Weigh About 1 gram	Actual Weight
A Coin	2g
A Pencil	4g
A Sharpener	3g

E. Circle the correct unit of weight for each estimation.

Question 1.
A box of cereal weighs about 350 (grams / kilograms).

Question 2.
A watermelon weighs about 3 (grams / kilograms).

Question 3.
A postcard weighs about 6 (grams / kilograms).

Question 4.
A cat weighs about 4 (grams / kilograms).

Question 5.
A bicycle weighs about 15 (grams / kilograms).

Question 6.
A lemon weighs about 58 (grams / kilograms).

F. During the exploration, Derrick finds that his bottle of water weighs the same as a 1-kilogram bag of rice. He then exclaims, “Our class laptop weighs the same as 2 bottles of water!” How much does the laptop weigh in kilograms? Explain your reasoning.

Answer:
The laptop weighs 2kg.

Explanation:
Derrick finds that his bottle of water weighs the same as a 1-kilogram bag of rice and he says that class laptop weighs the same as 2 bottles of water.So, If 1 bottle of water weighs 1 kg then 2 bottles of water weighs 2 kg.Therefore laptop weighs 2kg.

G. Nessa tells her brother that 1 kilogram of rice weighs the same as 10 bags containing 100 grams of beans each. Do you agree with her? Explain why or why not.

Answer:
Yes, 1 kilogram of rice weighs the same as 10 bags containing 100 grams of beans each.

Explanation:
Yes, because 10 X 100g=1000g and as we know 1000g is equal to 1 kilogram.

Engage NY Math 3rd Grade Module 2 Lesson 7 Exit Ticket Answer Key

Question 1.
Read and write the weights below. Write the word kilogram or gram with the measurement.
$Engage NY Math 3rd Grade Module 2 Lesson 7 Exit Ticket Answer Key 1$

$Engage NY Math 3rd Grade Module 2 Lesson 7 Exit Ticket Answer Key 1.1$

Question 2.
Circle the correct unit of weight for each estimation.
a. An orange weighs about 200 (grams / kilograms).

b. A basketball weighs about 624 (grams / kilograms).

c. A brick weighs about 2 (grams / kilograms).

d. A small packet of sugar weighs about 4 (grams / kilograms).

e. A tiger weighs about 190 (grams / kilograms).

Eureka Math 3rd Grade Module 2 Lesson 7 Homework Answer Key

Question 1.
Match each object with its approximate weight.
$Eureka Math 3rd Grade Module 2 Lesson 7 Homework Answer Key 2$

Question 2.
Alicia and Jeremy weigh a cell phone on a digital scale. They write down 113 but forget to record the unit. Which unit of measurement is correct, grams or kilograms? How do you know?

Question 3.
Read and write the weights below. Write the word kilogram or gram with the measurement.
$Eureka Math 3rd Grade Module 2 Lesson 7 Homework Answer Key 3$

$Eureka Math 3rd Grade Module 2 Lesson 7 Homework Answer Key 4$

$Eureka Math 3rd Grade Module 2 Lesson 7 Homework Answer Key 5$

$Eureka Math 3rd Grade Module 2 Lesson 7 Homework Answer Key 6$

$Eureka Math 3rd Grade Module 2 Lesson 7 Homework Answer Key 7$

Eureka Math Grade 3 Module 2 Answer Key

Eureka Math Grade 3 Module 2 Lesson 6 Answer Key

April 1, 2022March 23, 2021 by Prasanna

Engage NY Eureka Math 3rd Grade Module 2 Lesson 6 Answer Key

Eureka Math Grade 3 Module 2 Lesson 6 Problem Set Answer Key

Question 1.
Illustrate and describe the process of making a 1-kilogram weight.

Answer:

Explanation:
I put a 1 kg beans on one side of the pan balance.Then i filled a bag of rice on the other side of pan until the pan gets balanced.

Question 2.
Illustrate and describe the process of decomposing 1 kilogram into groups of 100 grams.

Answer:

Explanation:
I drew a ten-frame on the 1kg bag of rice.Each part of frame is 100g.There are 10 hundreds which is equal to 1000g.

Question 3.
Illustrate and describe the process of decomposing 100 grams into groups of 10 grams.

Answer:

Explanation:
I erased one of the 100g labels and drew a new ten frame .Each part of ten frame is 10g.There are 10 tens which is equal to 100g.

Question 4.
Illustrate and describe the process of decomposing 10 grams into groups of 1 gram.

Answer:

Explanation:
I erases one of the 10g labels and drew a new ten frame.Each part of new frame is 1g.There are 10 ones which is equal to 10 g.

Question 5.
Compare the two place value charts below. How does today’s exploration using kilograms and grams relate to your understanding of place value?

1 kilogram	100 grams	10 grams	1 gram

Thousands	Hundreds	Tens	Ones

Answer:
Todays exploration with weights relates to place value because 1 tens is equal to 10 ones, 1 hundreds is equal to 10 tens and 1 thousands is equal to 10 hundreds.The weights we used today also worked in the same way.10g is ten 1g, 100g is ten 10g and the 1000g is ten 100g.

Eureka Math Grade 3 Module 2 Lesson 6 Exit Ticket Answer Key

Ten bags of sugar weigh 1 kilogram. How many grams does each bag of sugar weigh?

Answer:

Explanation:
If I drew a ten frame on the 1kg bag of sugar, Each part of ten frame is 100g.So, If ten bags of sugar weigh 1kg then each bag of sugar weighs 100g.

Eureka Math Grade 3 Module 2 Lesson 6 Homework Answer Key

Question 1.
Use the chart to help you answer the following questions:

1 kilogram	100 grams	10 grams	1 gram

a. Isaiah puts a 10-gram weight on a pan balance. How many 1-gram weights does he need to balance the scale?

Answer:
As we know one 10g is equal to ten 1g.So, needs to put ten 1g to balance the scale.

b. Next, Isaiah puts a 100-gram weight on a pan balance. How many 10-gram weights does he need to balance the scale?

Answer:
As we know one 100g is equal to ten 10g.So, needs to put ten 10g to balance the scale.

c. Isaiah then puts a kilogram weight on a pan balance. How many 100-gram weights does he need to balance the scale?

Answer:
As we know one 1000g is equal to ten 100g.So, needs to put ten 100g to balance the scale.

d. What pattern do you notice in Parts (a–c)?

Answer:
I noticed here the pattern of place values.1 tens is equal to 10 ones, 1 hundreds is equal to 10 tens and 1 thousands is equal to 10 hundreds.In the same way one 10g is ten 1g, one100g is ten 10g and the one 1000g is ten 100g

Question 2.
Read each digital scale. Write each weight using the word kilogram or gram for each measurement.
$Eureka Math 3rd Grade Module 2 Lesson 6 Homework Answer Key 1$

$Eureka Math 3rd Grade Module 2 Lesson 6 Homework Answer Key 2$

$Eureka Math 3rd Grade Module 2 Lesson 6 Homework Answer Key 3$

$Eureka Math 3rd Grade Module 2 Lesson 6 Homework Answer Key 4$

$Eureka Math 3rd Grade Module 2 Lesson 6 Homework Answer Key 5$

$Eureka Math 3rd Grade Module 2 Lesson 6 Homework Answer Key 6$

Eureka Math Grade 3 Module 2 Answer Key

Eureka Math Grade 3 Module 2 Lesson 5 Answer Key

April 1, 2022March 23, 2021 by Prasanna

Engage NY Eureka Math 3rd Grade Module 2 Lesson 5 Answer Key

Eureka Math Grade 3 Module 2 Lesson 5 Problem Set Answer Key

Question 1.
Cole read his book for 25 minutes yesterday and for 28 minutes today. How many minutes did Cole read altogether? Model the problem on the number line, and write an equation to solve.
$Eureka Math Grade 3 Module 2 Lesson 5 Problem Set Answer Key 1$
Cole read for __________ minutes.

Answer:

Explanation:
Cole read his book for 25 minutes yesterday and for 28 minutes today.
25+28=53
Cole read altogether 53 minutes.

Question 2.
Tessa spends 34 minutes washing her dog. It takes her 12 minutes to shampoo and rinse and the rest of the time to get the dog in the bathtub! How many minutes does Tessa spend getting her dog in the bathtub? Draw a number line to model the problem, and write an equation to solve.

Answer:

Explanation:
Tessa spends 34 minutes washing her dog. It takes her 12 minutes to shampoo and rinse and the rest of the time to get the dog in the bathtub.
34-12=22
Tessa spend getting her dog in the bathtub for about 22 minutes.

Question 3.
Tessa walks her dog for 47 minutes. Jeremiah walks his dog for 30 minutes. How many more minutes did tessa walks her dog than jeremiah?

Answer:

Explanation:
Tessa walks her dog for 47 minutes. Jeremiah walks his dog for 30 minutes
47-30=17
17 more minutes tessa walks her dog than jeremiah

Question 4.
a. It takes Austin 4 minutes to take out the garbage, 12 minutes to wash the dishes, and 13 minutes to mop the kitchen floor. How long does it take Austin to do his chores?
b. Austin’s bus arrives at 7:55 a.m. If he starts his chores at 7:30 a.m., will he be done in time to meet his bus? Explain your reasoning.

Answer:

Explanation:
It takes Austin 4 minutes to take out the garbage, 12 minutes to wash the dishes, and 13 minutes to mop the kitchen floor.
4+12+13=29
It take Austin to do his chores for about 29 minutes.

Explanation:
Austin’s bus arrives at 7:55 a.m. If he starts his chores at 7:30 a.m., will he be done in time to meet his bus.
It take Austin to do his chores for about 29 minutes, If he starts his chores at 7:30am he cannot finish the work within 25min as the bus starts at 7:55am.

Question 5.
Gilberto’s cat sleeps in the sun for 23 minutes. It wakes up at the time shown on the clock below. What time did the cat go to sleep?
$Eureka Math Grade 3 Module 2 Lesson 5 Problem Set Answer Key 2$

Answer:

Explanation:
Gilberto’s cat sleeps in the sun for 23 minutes. It wakes up at the time 11:36.So, the cat sleeps for 23 minutes.

Eureka Math Grade 3 Module 2 Lesson 5 Exit Ticket Answer Key

Michael spends 19 minutes on his math homework and 17 minutes on his science homework.
How many minutes does Michael spend doing his homework?

Model the problem on the number line, and write an equation to solve.
$Engage NY Math 3rd Grade Module 2 Lesson 5 Exit Ticket Answer Key 3$
Michael spends __________ minutes on his homework.

Answer:

Explanation:
Michael spends 19 minutes on his math homework and 17 minutes on his science homework
19+17=36
Michael spends 36 minutes on his homework

Eureka Math Grade 3 Module 2 Lesson 5 Homework Answer Key

Question 1.
Abby spent 22 minutes working on her science project yesterday and 34 minutes working on it today. How many minutes did Abby spend working on her science project altogether? Model the problem on the number line, and write an equation to solve.
$Eureka Math 3rd Grade Module 2 Lesson 5 Homework Answer Key 4$
Abby spent __________ minutes working on her science project.

Answer:

Explanation:
Abby spent 22 minutes working on her science project yesterday and 34 minutes working on it today
22+34=56
Abby spent 56 minutes working on her science project

Question 2.
Susanna spends a total of 47 minutes working on her project. How many more minutes than Susanna does Abby spend working? Draw a number line to model the problem, and write an equation to solve.

Answer:

Explanation:
Abby spents 56minutes and susanna spents 47 minutes to work on their projects.
56-47=9 minutes.
Abby spend working 9 minutes more than Susanna.

Question 3.
Peter practices violin for a total of 55 minutes over the weekend. He practices 25 minutes on Saturday. How many minutes does he practice on Sunday?

Answer:

Explanation:
Peter practices violin for total of 55 minutes over the weekend
He practices 25 minutes on Saturday.
55-25=30
Peter practices violin for 30 minutes on sunday.

Question 4.
a. Marcus gardens. He pulls weeds for 18 minutes, waters for 13 minutes, and plants for 16 minutes. How many total minutes does he spend gardening?
b. Marcus wants to watch a movie that starts at 2:55 p.m. It takes 10 minutes to drive to the theater. If Marcus starts the yard work at 2:00 p.m., can he make it on time for the movie? Explain your reasoning.

Answer:

Explanation:
Marcus gardens. He pulls weeds for 18 minutes, waters for 13 minutes, and plants for 16 minutes
18+13+16=47
Marcus spend gardening for a total of 47 minutes.

Explanation:
Marcus wants to watch a movie that starts at 2:55 p.m. It takes 10 minutes to drive to the theater. If Marcus starts the yard work at 2:00 p.m, he cannot reach the movie on time as it takes 57 minutes for him to reach but he has only 55 minutes.

Question 5.
Arelli takes a short nap after school. As she falls asleep, the clock reads 3:03 p.m. She wakes up at the time shown below. How long is Arelli’s nap?
$Eureka Math 3rd Grade Module 2 Lesson 5 Homework Answer Key 5$

Answer:

Explanation:
Arelli takes a short nap after school. As she falls asleep, the clock reads 3:03 p.m. She wakes up at the time 3:30pm
30-3=27
So,

Eureka Math Grade 3 Module 2 Answer Key

Eureka Math Grade 3 Module 2 Lesson 4 Answer Key

April 1, 2022March 23, 2021 by Prasanna

Engage NY Eureka Math 3rd Grade Module 2 Lesson 4 Answer Key

Eureka Math Grade 3 Module 2 Lesson 3 Answer Key

April 1, 2022March 23, 2021 by Prasanna

Engage NY Eureka Math 3rd Grade Module 2 Lesson 3 Answer Key

Eureka Math Grade 3 Module 2 Lesson 3 Problem Set Answer Key

Question 1
Plot a point on the number line for the times shown on the clocks below. Then, draw a line to match the clocks to the points.
$Eureka Math Grade 3 Module 2 Lesson 3 Problem Set Answer Key 1$

Answer:

Explanation:
The red lines shows the time 7:17pm, the pink line shows 7:03pm, the green line shows the time 7:55pm and the blue line shows the time 7:42pm on the number line.

Question 2.
Jessie woke up this morning at 6:48 a.m. Draw hands on the clock below to show what time Jessie woke up.
$Eureka Math Grade 3 Module 2 Lesson 3 Problem Set Answer Key 2$

Answer:

Explanation:
To show the time 6:48am in the clock draw the hours hand on six and minutes hand between 9 and 10.

Question 3.
Mrs. Barnes starts teaching math at 8:23 a.m. Draw hands on the clock below to show what time Mrs. Barnes starts teaching math.
$Eureka Math Grade 3 Module 2 Lesson 3 Problem Set Answer Key 3$

Answer:

Explanation:
To show the time 8:23am in the clock draw the hours hand on 8 and minutes hand between 4 and 5.

Question 4.
The clock shows what time Rebecca finishes her homework. What time does Rebecca finish her homework?
$Eureka Math Grade 3 Module 2 Lesson 3 Problem Set Answer Key 4$
Rebecca finishes her homework at _______________.

Answer:
Rebecca finishes her homework at 5:27pm.

Explanation:
As the hours hand is pointed between 5 and 6 and the minutes hand is placed between 25 and 30, The time is 5 hours and 27 minutes.

Question 5.
The clock below shows what time Mason’s mom drops him off for practice.
a. What time does Mason’s mom drop him off?
$Eureka Math Grade 3 Module 2 Lesson 3 Problem Set Answer Key 5$
b. Mason’s coach arrived 11 minutes before Mason. What time did Mason’s coach arrive?

Answer:

Explanation:
As the hours hand is pointing 4 and the minutes hand 9 ie 45 minutes, The time is 3:45.Therefore Mason’s coach arrived at 3:45.

Eureka Math Grade 3 Module 2 Lesson 3 Exit Ticket Answer Key

The clock shows what time Jason gets to school in the morning.
a. What time does Jason get to school?
$Engage NY Math 3rd Grade Module 2 Lesson 3 Exit Ticket Answer Key 6$

Answer:
Jason gets to school at 8:04am in the morning.

Explanation:
A the clock shows the hours hand on 8 and the minutes hand on 4 so, the time is 8:04am.

b. The first bell rings at 8:23 a.m. Draw hands on the clock to show when the first bell rings.
$Engage NY Math 3rd Grade Module 2 Lesson 3 Exit Ticket Answer Key 7$

Answer:

Explanation:
As the first bell rings at 8:23am point the hours hand at 8 and the minutes hands between 4 and 5 ie 20 and 25.

c. Label the first and last tick marks 8:00 a.m. and 9:00 a.m. Plot a point to show when Jason arrives at school. Label it A. Plot a point on the line when the first bell rings and label it B.
$Engage NY Math 3rd Grade Module 2 Lesson 3 Exit Ticket Answer Key 7.1$

Answer:

Explanation:
The first and last tick marks are 8:00am and 9:00am.The pointed marks on the number line are A Jason gets to school at 8:04am and B first bell rings at 8:23am.

Eureka Math Grade 3 Module 2 Lesson 3 Homework Answer Key

Question 1.
Plot points on the number line for each time shown on a clock below. Then, draw lines to match the clocks to the points.
$Eureka Math 3rd Grade Module 2 Lesson 3 Homework Answer Key 8$

Answer:

Explanation:
The red lines shows the time 04:34pm, the pink line shows 04:53pm, the green line shows the time 04:16pm and the orange line shows the time 4:01pm on the number line.

Question 2.
Julie eats dinner at 6:07 p.m. Draw hands on the clock below to show what time Julie eats dinner.
$Eureka Math 3rd Grade Module 2 Lesson 3 Homework Answer Key 9$

Answer:

Explanation:
To show the time 06:07am in the clock draw the hours hand on 6 and minutes hand between 1 and 2.

Question 3.
P.E. starts at 1:32 p.m. Draw hands on the clock below to show what time P.E. starts.
$Eureka Math 3rd Grade Module 2 Lesson 3 Homework Answer Key 10$

Answer:

Explanation:
To show the time 1:32am in the clock draw the hours hand on 1 and minutes hand between 6 and 7.

Question 4.
The clock shows what time Zachary starts playing with his action figures.
a. What time does he start playing with his action figures?
$Eureka Math 3rd Grade Module 2 Lesson 3 Homework Answer Key 11$

Explanation:
As the hours hand on 2 and the minutes hand between 6 and 7.So, the time 2:32.

b. He plays with his action play finishes after 23 minutes.What time does he finish playing?
c. Draw hands on the clock to the right to show what time Zachary finishes playing.
$Eureka Math 3rd Grade Module 2 Lesson 3 Homework Answer Key 12$

Answer:

Explanation:
Zachary finishes playing after 23 minutes from P.E. at 1:32 p.m. so, the time is 1:55.Mark the hours hand on 1 and the minutes hand on 11 ie 55 minutes.

d. Label the first and last tick marks with 2:00 p.m. and 3:00 p.m. Then, plot Zachary’s start and finish times. Label his start time with a B and his finish time with an F.
$Eureka Math 3rd Grade Module 2 Lesson 3 Homework Answer Key 13$

Answer:

Explanation:
The first and last tick marks are labled with the timings 2:00 p.m. and 3:00 p.m.The start and finish time of Zachary are marked as B the start time(2:32) and F the finish time(2:55).

Eureka Math Grade 3 Module 2 Answer Key

Eureka Math Grade 3 Module 2 Lesson 2 Answer Key

April 1, 2022March 23, 2021 by Prasanna

Engage NY Eureka Math 3rd Grade Module 2 Lesson 2 Answer Key

Eureka Math Grade 3 Module 2 Lesson 2 Problem Set Answer Key

Question 1.
Follow the directions to label the number line below.
$Eureka Math Grade 3 Module 2 Lesson 2 Problem Set Answer Key 1$
a. Ingrid gets ready for school between 7:00 a.m. and 8:00 a.m. Label the first and last tick marks as 7:00 a.m. and 8:00 a.m.
b. Each interval represents 5 minutes. Count by fives starting at 0, or 7:00 a.m. Label each 5-minute interval below the number line up to 8:00 a.m.
c. Ingrid starts getting dressed at 7:10 a.m. Plot a point on the number line to represent this time. Above the point, write D.
d. Ingrid starts eating breakfast at 7:35 a.m. Plot a point on the number line to represent this time. Above the point, write E.
e. Ingrid starts brushing her teeth at 7:40 a.m. Plot a point on the number line to represent this time. Above the point, write T.
f. Ingrid starts packing her lunch at 7:45 a.m. Plot a point on the number line to represent this time. Above the point, write L.
g. Ingrid starts waiting for the bus at 7:55 a.m. Plot a point on the number line to represent this time. Above the point, write W.

Answer:

Explanation:
The number line above shows the following points
The point D shows Ingrid begins getting dressed(7:10am)
The point E shows Ingrid begins Eating breakfast(7:35am)
The point T shows Ingrid begins brussing her teeth(7:40am)
The point L shows Ingrid begins packing her lunch(7:45am)
The point W shows Ingrid begins waiting for the bus(7:55am).

Question 2.
Label every 5 minutes below the number line shown. Draw a line from each clock to the point on the number line which shows its time. Not all of the clocks have matching points.
$Eureka Math Grade 3 Module 2 Lesson 2 Problem Set Answer Key 2$

Answer:

Explanation:
The black line points the time 05:50 am,the red line points the time 05:15am, the pink line points the time 05:25am and the orange line points the time 05:40am.

Question 3.
Noah uses a number line to locate 5:45 p.m. Each interval is 5 minutes. The number line shows the hour from 5 p.m. to 6 p.m. Label the number line below to show his work.
$Eureka Math Grade 3 Module 2 Lesson 2 Problem Set Answer Key 3$

Answer:

Explanation:
Noah wanted to point the 5:45pm.Draw a number line lable the points of number line with intervels of 5 starting from 0 to 60.Mark 45 and this point will be the time 5:45 that Noah wanted to locate.

Question 4.
Tanner tells his little brother that 11:25 p.m. comes after 11:20 a.m. Do you agree with Tanner? Why or why not?

Answer:
I donot agree with tanner because after 11:20 am comes 11:25 am not 11:25 pm.AM AntiMeridian means before midday and PM PostMeridian means after midday.

Eureka Math Grade 3 Module 2 Lesson 2 Exit Ticket Answer Key

The number line below shows a math class that begins at 10:00 a.m. and ends at 11:00 a.m. Use the number line to answer the following questions.

$Eureka Math Grade 3 Module 2 Lesson 2 Exit Ticket Answer Key 4$

a. What time do Sprints begin?
b. What time do students begin the Application Problem?
c. What time do students work on the Exit Ticket?

d. How long is math class?

Answer:
a
Sprints begin at 10:10am.

Explanation:
As sprints is located on 10 min mark on number line it means the time is 10:10 am.

b
Students begin application problems at 10:20 am.

Explanation:
As application problem is located on 20 min mark on number line it means the time is 10:20 am.

c
Students work on Exit Ticket at 10:50am

Explanation:
As Exit ticket is located on 50 min mark on number line it means the time is 10:50 am.

d
The math class is 1 hour long because the number line denotes 60 minutes from 0 to 60 that is from 10am to 11am.

Eureka Math Grade 3 Module 2 Lesson 2 Homework Answer Key

Follow the directions to label the number line below.
$Eureka Math Grade 3 Module 2 Lesson 2 Homework Answer Key 5$
a. The basketball team practices between 4:00 p.m. and 5:00 p.m. Label the first and last tick marks as 4:00 p.m. and 5:00 p.m.
b. Each interval represents 5 minutes. Count by fives starting at 0, or 4:00 p.m. Label each 5-minute interval below the number line up to 5:00 p.m.
c. The team warms up at 4:05 p.m. Plot a point on the number line to represent this time. Above the point, write W.
d. The team shoots free throws at 4:15 p.m. Plot a point on the number line to represent this time. Above the point, write F.
e. The team plays a practice game at 4:25 p.m. Plot a point on the number line to represent this time. Above the point, write G.
f. The team has a water break at 4:50 p.m. Plot a point on the number line to represent this time. Above the point, write B.
g. The team reviews their plays at 4:55 p.m. Plot a point on the number line to represent this time. Above the point, write P.

Answer:

Explanation:
The number line above shows the following points
The point W shows the team warms up(4:05pm)
The point F shows the team shoots free throws(4:15pm)
The point G shows the team plays a practice game(4:25pm)
The point B shows the team has a water break(4:50pm)
The point P shows the team reviews their plays(4:55pm).

Eureka Math Grade 3 Module 2 Answer Key

Addition of Mixed Fractions – Definition, Examples | How to Add Mixed Fractions with Like and Unlike Denominators?

April 1, 2022March 23, 2021 by Prasanna

Looking for ways on How to Add Mixed Fractions? If so, halt your search as we have listed all about Mixed Fractions Addition and different methods of it clearly in the later modules. Mixed Fractions are one of the types of fractions. These are also called Mixed Numbers. Go through the entire article to be well versed with the details like Adding Mixed Fractions Definition, How to Add Mixed Fractions with Same and Different Denominators, Examples, etc.

Mixed Fraction – Definition

A Mixed Fraction is a form of a fraction that has a whole number next to a fraction.

Example: 3 $\frac { 1 }{ 5 } $ where 3 is a whole number and $\frac { 1 }{ 5 } $ is a fraction.

How to Add Mixed Numbers?

When it comes to Adding Mixed Fractions we can have either the same or different denominators for both the fractions to be added. There are two different methods for Adding Mixed Numbers with Like, Unlike Denominators. Here is a Step by Step Procedure on How to Add Mixed Fractions. They are as such

Method 1: Adding the Whole Numbers and Fractions Separately

In the first step add the whole numbers separately.
In order to add fractions with the same denominator, simply add the numerators and keep the denominator unaltered. However, if you have different or unlike denominators take the LCM of them and change to Like Fractions.
Once, you have a Common Denominator adding fractions is much simpler.
Find the Sum of Whole Numbers and Fractions in Simplest Form.

Method 2: Convert Mixed Numbers to Improper Fractions and then Add them

Initially, change the given Mixed Fractions to Improper Fractions.
If Denominators of the Improper Fractions are the same simply add the numerators. If the Denominators of Improper Fractions are Unlike or Different take the LCM of Denominators and change them to like fractions.
Add Like Fractions and express the sum to its Simplest Form.

Also, Check:

Examples on Adding Mixed Fractions using Method 1

1. Add 3 $\frac { 1 }{ 3 } $, 2 $\frac { 1 }{ 4} $?

Solution:

3 $\frac { 1 }{ 3 } $+ 2 $\frac { 1 }{ 4} $

Let us add the whole numbers and fraction parts separately i.e.

Whole Numbers Part 3+2 = 5

Fractions Part = $\frac { 1 }{ 3 } $+ $\frac { 1 }{ 4} $

Since the denominators of the fractions are not same find the LCM of the Denominators to make them like fractions

LCM(3,4) = 12

$\frac { 1*4 }{ 3*4 } $ + $\frac { 1*3 }{ 4*3} $

= $\frac { 4 }{ 12 } $ + $\frac { 3 }{ 12 } $

= $\frac { (4+3) }{ 12 } $

= $\frac { 7 }{ 12 } $

Now add the like fractions and express the sum to its simplest form

= 5 $\frac { 7 }{ 12 } $

Therefore, 3 $\frac { 1 }{ 3 } $, 2 $\frac { 1 }{ 4} $ when added gives 5 $\frac { 7 }{ 12 } $

2. Add 5 $\frac { 1 }{ 4} $, 2 $\frac { 1 }{ 5} $, $\frac { 1 }{ 6 } $?

Solution:

5 $\frac { 1 }{ 4} $ + 2 $\frac { 1 }{ 5} $ + $\frac { 1 }{ 6 } $

Firstly, let us add the whole numbers and fraction parts separately i.e.

Whole Numbers Part (5+2+0) = 7

Fractions Part = $\frac { 1 }{ 4} $ + $\frac { 1 }{ 5} $ + $\frac { 1 }{ 6 } $

Since the Denominators of Fractions aren’t the same find the LCM of Denominators and express them as like fractions

LCM(4, 5, 6) = 60

= $\frac { (1*15) }{ (4*15) } $ + $\frac { (1*12) }{ (5*12)} $ + $\frac { (1*10) }{ (6*10) } $

= $\frac { 15 }{ (60) } $ + $\frac { 12 }{ 60} $ + $\frac { 10 }{ 60 } $

= $\frac { (15+12+10) }{ 60 } $

= $\frac { 37 }{ 60 } $

Now add the like fractions and express the sum to its simplest form

= 7 $\frac { 37 }{ 60 } $

Therefore, 5 $\frac { 1 }{ 4} $, 2 $\frac { 1 }{ 5} $, $\frac { 1 }{ 6 } $ when added gives 7 $\frac { 37 }{ 60 } $

Adding Mixed Fractions Examples using Method 2

1. Add 5 $\frac { 1 }{ 4 } $, 3 $\frac { 1 }{ 2 } $?

Solution:

5 $\frac { 1 }{ 4 } $ + 3 $\frac { 1 }{ 2 } $

Change the given Mixed Numbers to Improper Fractions

= $\frac { (5*4+1) }{ 4 } $ + $\frac { (3*2+1) }{ 2 } $

= $\frac { 21 }{ 4 } $ + $\frac { 7 }{ 2 } $

Since the Denominators aren’t same find the LCM and express them as Like Fractions

LCM(4,2) = 2

= $\frac { (21*1) }{ 4*1 } $ + $\frac { (7*2) }{ (2*2) } $

= $\frac { 21 }{ 4 } $ + $\frac { 14 }{ 4 } $

= $\frac { (21+14) }{ 4 } $

= $\frac { 35 }{ 4 } $

Thus, 5 $\frac { 1 }{ 4 } $, 3 $\frac { 1 }{ 2 } $ added results in $\frac { 35 }{ 4 } $

2. Add 6 $\frac { 1 }{ 4 } $, 7 $\frac { 1 }{ 4 } $, 3 $\frac { 1 }{ 4 } $?

Solution:

6 $\frac { 1 }{ 4 } $ + 7 $\frac { 1 }{ 4 } $ + 3 $\frac { 1 }{ 4 } $

Change the given Mixed Fractions to Improper Fractions

= $\frac { (6*4+1) }{ 4 } $ + $\frac { (7*4+1) }{ 4 } $ + $\frac { (3*4+1) }{ 4 } $

= $\frac { 25 }{ 4 } $ + $\frac {29 }{ 4 } $ + $\frac { 13 }{ 4 } $

= $\frac { (25+29+13) }{ 4 } $

= $\frac { 67 }{ 4 } $

Thus, 6 $\frac { 1 }{ 4 } $, 7 $\frac { 1 }{ 4 } $, 3 $\frac { 1 }{ 4 } $ results in $\frac { 67 }{ 4 } $

FAQs on Adding Mixed Fractions

1. What is a Mixed Fraction with Example?

A Mixed Fraction is a form of a fraction that has a whole number next to a fraction. For Example 6 $\frac { 1 }{ 4 } $ is a Mixed Fraction where 6 is a whole number and $\frac { 1 }{ 4 } $ is the fraction part.

2. What does a Mixed Fraction look like?

Mixed Fraction is simply an improper fraction written as the sum of a whole number and a proper fraction. For instance, improper fraction $\frac { 5 }{ 2 } $ can be written as Mixed Fraction 2 $\frac { 1 }{ 2 } $.

3. How to add Mixed Fractions Step by Step?

Follow the simple and easy steps listed below to add Mixed Fractions and they are as such

Convert the given Mixed Fractions to Improper Fractions
Find the LCM of Denominators and then make them like fractions.
Add the Like Fractions and Express the Sum to its Simplest Form.

Perimeter of Quadrilateral – Definition, Formula, Examples | How to Find the Perimeter of Quadrilateral?

April 1, 2022March 23, 2021 by Prasanna

The perimeter is the distance around a shape. A quadrilateral is a polygon that has four sides and four angles. To find the perimeter of a quadrilateral adds the measurements of four sides of it. We have given the most common types of quadrilaterals along with the perimeter of that quadrilateral. Check out the complete article and know how to find the perimeter of the quadrilateral. Some of the examples of a quadrilateral are Parallelogram, Rectangle, Square, Rhombus, and Trapezium, etc.

Also, Read:

Perimeter of Different Types of Quadrilaterals

The sum of the four angles of the quadrilateral is equal to 360°. We have different types of quadrilateral. They are

Parallelogram
Rectangle
Square
Rhombus
Trapezium

The perimeter of the Quadrilateral is the sum of the distance around the image. That means the perimeter of a quadrilateral is equal to the sum of the four sides of the image or object. That is,

(AB + BD + DC + CA) = Perimeter of the Quadrilateral.

1. Parallelogram

Here, the lengths of the two sides of the parallelogram are equal and the breadths of the two sides of the parallelogram are equal. Opposite sides are equal in a parallelogram.
Perimeter of the Parallelogram = (AB + BD + DC + CA)
= (b + l + b + l).
Perimeter of the Parallelogram = 2(l + b).
Here, ‘l’ represents the length and ‘b’ represents the breadth of the parallelogram.
Area of the parallelogram = Base * height.

2. Rectangle

In a rectangle, both the lengths of the sides are equal and the breadths of the sides of a rectangle are equal. That means, opposite sides of the rectangle are equal.
Perimeter of the rectangle = (AB + BD + DC + CA) = (b + l + b + l) = 2(l + b).
Perimeter of the Rectangle = 2(l + b).
Area of the Rectangle = length * breadth = l *b.
Here, ‘l’ indicates the length of the rectangle and ‘b’ indicates the breadth of the rectangle.

3. Square

In this, a square is also enclosed with the four sides and the lengths of these four sides are equal.
Here, ‘a’ indicates the length of the sides of the square.
Perimeter of the square = (AB + BD + DC + CA) = (a + a + a + a) = 4a.
The perimeter of the square = 4a.
Area of the Square = Side * Side = a * a = a^2.

4. Rhombus

The lengths of the four sides of the rhombus are equal. Here, ‘a’ represents the length of the side.
Perimeter of the Rhombus = (AB + BC + CD + DA) = (a + a + a + a) = 4a.
The perimeter of the Rhombus = 4a.
Area of the Rhombus = (Base * height).

5. Trapezium

Two opposite sides of the trapezium are parallel. Perimeter of the Trapezium = (AB + BC + CD + DA).
AB + BC + CD + DA = (c + b + d + a)cm.
Area of the Trapezium = (a + b) / 2 * h.
Here, a, b, c, d are the sides of the trapezium. And ‘h’ indicates the height of the trapezium.

Perimeter of Quadrilateral Examples

1. Find the Perimeter of the Quadrilateral with the sides 2cm, 10cm, 5cm, and 20cm?

Solution:
The given information is the length of the four sides of the quadrilateral is = 2cm, 10cm, 5cm, 20cm.
The perimeter of the quadrilateral = sum of the length of the four sides of the quadrilateral.
Perimeter of the quadrilateral = (2 + 10 + 5 + 20)cm. = 37cm.

So, the perimeter of the quadrilateral is equal to 37cm.

2. The Perimeter of the quadrilateral is 40cm and the length of the three sides of the quadrilateral is 5cm, 10cm, and 5cm. Find the length of the four sides of the quadrilateral?

Solution:
The given details are the Perimeter of the quadrilateral = 40cm.
Length of the three sides of quadrilateral = 5cm, 10cm, and 5cm.
The perimeter of the quadrilateral = sum of the length of four sides of the quadrilateral.
40cm = (5 + 10 + 5 + x) cm.
40 = 20 + x.
x = 40 – 20 = 20cm.

Finally, the length of the fourth side of the quadrilateral is equal to 20cm.

3. A woman crosses a distance of 24m long while going round a quadrilateral field twice. What will be the cost of fencing the field at the rate of cost $1.20per m?

Solution:
The given information is Women crosses a distance of 24m long = perimeter of its boundary = 24 / 2 = 12m.
Cost of fencing the field for 1m = $1.20.
Then the cost of 12m of fencing the field = 12 * $1.20 = $14.4.

Therefore, the cost of the 12m fencing field is equal to $14.4.

4. One side of the square is 4cm. Find the perimeter of the square?

Solution:
As per the given information, the length of the side of the square = 4cm.
The perimeter of the square = 4a.
Here, a = 4.
By substituting the ‘a’ value in the formulae, we will get
Perimeter of the square = 4 * 4 = 16cm.

So, the perimeter of the square is equal to 16cm.

5. Length of the rectangle is 10cm and the breadth of the rectangle is 5cm. Calculate the Perimeter of the Rectangle?

Solution:
As per the given details, the Length of the rectangle (l) = 10cm.
Breadth of the rectangle (b) = 5cm.
Perimeter of the rectangle = 2(l + b).
By substituting the values in the formulae, we will get like
Perimeter of the rectangle = 2(10 + 5) = 2(15) = 30cm.

Therefore, the perimeter of the rectangle is equal to 30cm.

6. If the area of the rhombus is 20 square units and the height of the rhombus is 6 units, then calculate the base of the rhombus?

Solution:
From the given information, Area of the Rhombus = 20 Sq units.
Height of the Rhombus (h) = 6 units.
Area of the Rhombus = Base * height.
20 = Base * 6.
Base = 20 / 6 = 10 / 3 = 0.3 units.

The base of the Rhombus is equal to 0.3 units.

Frequently Asked Questions

1. What is Quadrilateral?

The quadrilateral is enclosed with four sides. It has four corners, four angles, and four sides. The total angle of the quadrilateral is equal to 360°.

2. What are the types of Quadrilateral?

The types of Quadrilateral are,
1. Square
2. Rectangle
3. Parallelogram
4. Trapezium
5. Rhombus

3. How we can find the perimeter of a quadrilateral?

The area of the quadrilateral is the sum of all sides of the quadrilateral. Yes, by adding all sides of the quadrilateral, we can find the perimeter of the quadrilateral.

Decimals – Definition, Types, Properties, Conversions, Arithmetic Operations, Examples

April 1, 2022March 23, 2021 by Prasanna

In Maths Numbers are Classified into Various Types like Real Numbers, Whole Numbers, Natural Numbers, Rational Numbers, etc. Decimal Numbers is a Standard form among them used to represent integers and non-integer numbers. By going through this article, you will learn all about the Definition of Decimals, Types, Properties, Conversions, Examples, etc. in the later modules.

What are Decimals?

Decimals are one type of numbers that has a whole number and fractional part separated by a decimal point. The Dot present between the whole number part and fractional part is called the decimal point.

For instance, 23.4 is a decimal number in which 23 is a whole number and 4 is called the fractional part.

“.” is called the decimal point.

List of Decimal Concepts

Below is the list of Decimal Topics for your reference. You can access them by simply clicking on the quick links available. Once you click on them you will be redirected to a new page having the entire concept explained with examples. Try solving as much as possible to get a good grip on the concept.

Decimal Numbers
Decimal Fractions
Decimal Places
Decimal and Fractional Expansion
Like and Unlike Decimals
Conversion of Unlike Decimals to Like Decimals
Comparing Decimals
Adding Decimals
Subtracting Decimals
Simplify Decimals Involving Addition and Subtraction Decimals
Multiplying Decimal by a Whole Number
Multiplying Decimal by a Decimal Number
Dividing Decimal by a Whole Number
Dividing Decimal by a Decimal Number
Simplification of Decimal
Converting Decimals to Fractions
Converting Fractions to Decimals
Rounding Decimals
Rounding Decimals to the Nearest Whole Number
Rounding Decimals to the Nearest Tenths
Rounding Decimals to the Nearest Hundredths
Round a Decimal
H.C.F. and L.C.M. of Decimals
Terminating Decimal
Non-Terminating Decimal
Repeating or Recurring Decimal
Pure Recurring Decimal
Mixed Recurring Decimal
Conversion of Pure Recurring Decimal into Vulgar Fraction
Conversion of Mixed Recurring Decimals into Vulgar Fractions

Types of Decimal Numbers

Decimal Numbers are classified into two types namely

Recurring Decimal Numbers
Non-Recurring Decimal Numbers
Decimal Fraction

Recurring Decimal Numbers: These are also called Repeating or Non-Terminating Decimals. These Recurring Decimals are further classified into Finite and Infinite.

Example:

3.2525(Finite)

4.12121212……(Infinite)

Non-Recurring Decimal Numbers: These are also called Non-Repeating or Terminating Decimals. They are further classified into finite and infinite non-recurring decimal numbers.

Example:

5.2475 (Finite)

4.1367254….(Infinite)

Decimal Fraction: It Represents the fraction whose denominator is in powers of ten.

31.75 = 3175/100

22.415 = 22415/1000

In Order to Change the Decimal Number to Decimal Fraction firstly place 1 in the denominator and remove the decimal point. “1” is followed by zeros that are equal to the number of digits following the decimal point.

For Example to convert 2.345 to decimal fraction we get

22.345 = 2345/1000

2 represents the power of 10¹ that is the tenths position.

2 represents the power of 10⁰that is the unit’s position.

3 represents the power of 10^-1 that is the one-tenth position.

4 represents the power of 10^-2 that is the one-hundredths position.

5 represents the power of 10^-3 that is the one-thousandths position

This is how each digit is represented to the power of a decimal number.

Place Value in Decimals

Place Value System defines the position of a digit in a number that helps to determine its value. When we write Numbers Position of each digit is important.

Decimal Example

The position of “7” is in One’s place, which means 7 ones (i.e. 6).
The position of “2” is in the Ten’s place, which means 2 tens (i.e. twenty).
The position of “3” is in the Hundred’s place, which means 3 hundred.
As we go left, each position becomes ten times greater.

Therefore, we read it as Three Hundred Twenty-Seven

On Moving towards the left each position becomes 10 times bigger and

Tens are 10 times bigger than ones and similarly, Hundreds are 10 times bigger than Tens.

Decimal Place Value Towards Right

Moving towards the right each position becomes 10 times smaller from Hundreds to Tens to Ones. If we continue further the process after ones $\frac { 1 }{ 10 } $ths are smaller. Before doing so, you need to place a decimal point.

Decimal Point Example

Place Value Chart

For a better understanding of the concept of place value check out the Place Value Chart below.

Place Value Chart

Digits to the left of the decimal point are multiplied with positive powers of 10 in increasing order from right to left. In the same way, digits to the right of the decimal point are multiplied with negative powers of 10 in increasing order from left to right.

Example:

71.325

Decimal Expansion of the number is expressed as follows

{(7*10)+(1*1)} + {(3*0.1)+(2*0.01)+(5*0.001)}

Here, each number is multiplied with associated power of 10.

Decimals Properties

Below is the list of important properties of decimal numbers under both multiplication and division operations. They are as follows

Irrespective of the decimal numbers multiplied in any order the product remains unchanged.
On multiplying a whole number and decimal number in any order the product remains the same.
If a decimal fraction is multiplied by 1 product is the decimal fraction itself.
If you multiply a decimal fraction with zero the product is zero(0).
On dividing a decimal number with 1, the quotient is the decimal number itself.
If you divide a decimal number with the same number the quotient is 1.
If you divide 0 with any decimal the quotient becomes zero.
Division of a Decimal Number with 0 isn’t possible since the reciprocal of 0 doesn’t exist.

Arithmetic Operations on Decimals

Similar to performing Arithmetic Operations on Integers you can do the same with Decimals. Let us discuss important tips while performing arithmetic operations.

Addition: In Decimal Numbers Addition, line up the decimal points of given numbers and then add the numbers. If you don’t find the decimal point, the decimal is behind the number.

Subtraction: Decimal Subtraction is also similar to Decimal Addition. Just like Decimal Addition line up the decimal point of given numbers and subtract the values. To do the arithmetic operation use place holding zeros for your reference.

Multiplication: While Performing Multiplication of Decimal Numbers multiply similar to integers as if the decimal point is not present. Find the product and count the number of digits next to the decimal point in both the numbers. Count indicates how many numbers are needed after the decimal point in the product value.

Division: In Order to divide decimal numbers firstly move the digits so that the number becomes whole numbers. Perform Division Operation similar to Integers Division.

Decimal to Fraction Conversions

Conversion of Fraction to Decimal or Decimal to Fraction is quite simple. We have explained both the methods by even taking few examples. They are as follows

Decimal to Fraction Conversion

Numbers after the decimal points denotes tenths, hundredths, thousandths, and so on. While converting from decimal to fraction note down the decimal numbers in expanded form and then simplify the values.

Example 0.45

Expanded form of 0.45 is 45*($\frac { 1 }{ 100 } $) = $\frac { 45 }{ 100 } $ = $\frac { 9 }{ 20 } $

Fraction to Decimal Conversion

In order to change from fraction to decimal simply divide the numerator with the denominator

For example, $\frac { 9 }{ 2 } $ is a fraction. If it’s divided, we get 4.5

Problems on Decimals

Question 1.

Convert $\frac { 15 }{ 10 } $ to decimal?

Solution:

To change from fraction to decimal you just need to divide the numerator with the denominator

On dividing, we get the decimal value as 1.5

Question 2.

Express 3.35 in fraction form?

Solution:

The given decimal number is 3.35

The expanded form of 3.35 is

= 335 x ($\frac { 1 }{ 100 } $)

= $\frac { 335 }{ 100 } $

=$\frac { 67 }{ 20 } $

Hence, the equivalent fraction for 3.35is $\frac { 67 }{ 20 } $.

Types of Symmetry – Line, Translation, Rotational, Reflection, Glide | Different Types of Symmetry with Examples

April 1, 2022March 22, 2021 by Prasanna

Symmetry is one of the important concepts of geometry. If one part of the object looks like the same as another part of the object when we turn, flip, or slide, then it is called symmetry. If an object is not looking like another part of the object then it is called asymmetric.

To find out a given object is symmetric, we need to follow some steps. Firstly, draw a line on the middle of the image or object, and observe the image or object whether the left side of the object is the same as the right side or not. If the image is symmetrical, then the left side of the image is looking like a mirror image of the right side of the image or not. We can define different types of symmetries as below.

Also, Read:

Lines of Symmetry

Example Images of Symmetry

Line of Symmetry

An object is divided into two parts with the help of a line and the two parts are mirror images of an object, then it is called a line of symmetry. The line of symmetry is also called as ‘axis of symmetry’. The line may be either vertical or horizontal or diagonal.

Vertical Line of Symmetry

The above figure shows the hexagonal image divided into two parts with the help of a vertical line. Here, the vertical line divides the above image into two parts and these two parts are mirror images for each other. That means, both the parts of an image are the same. This type of symmetry is called as Vertical line of Symmetry.

Horizontal Line of Symmetry

The above diagram shows that the image is split into two parts with the help of a horizontal line. Here, the horizontal line dividing the above image into two parts, and these two parts are equal halves of the image. This type of symmetry is called a horizontal line of symmetry.

Diagonal Line of Symmetry

From the above diagram, an image is divided into two equal halves by the diagonal line. These two equal halves are mirror images of each other. This type of line of symmetry is called as Diagonal Line of Symmetry.

Again we have a number of types in line of symmetry. Yes, we can divide the image into a number of parts with the help of one line, two-line,s or more lines. Every part must be the mirror image of another.

One Line of Symmetry

By using the vertical or horizontal or diagonal line, we need to divide the image into equal halves and it is called one line of symmetry. Above mentioned, vertical, horizontal, and diagonal lines of symmetry are examples of one line of symmetry.

Two Lines of Symmetry

Same like one line of symmetry, in two lines of symmetry also we can use the vertical or horizontal or diagonal lines but we need to use only two lines to divide the image equally. This type of line of symmetry is called Two lines of Symmetry.

Infinite Lines of Symmetry

An image or object is divided into a number of parts with the help of a number of lines and these equal halves of the image. It is called Infinite Lines of Symmetry. These lines are either vertical or horizontal or diagonal lines.

Some Other Types of Symmetry

We have different types of symmetries considered depending on the various cases. They are

Translational Symmetry
Rotational Symmetry
Reflexive Symmetry
Glide Symmetry

1.Translational Symmetry

An object or image is moving forward or backward or changing the position from one place to another, but there is no change in the image or object. This type of Symmetry is called Translational Symmetry.

2.Rotational Symmetry

An object or image is rotated in a particular direction but the position of an object or image is identical to the origin of an image or object, then it is called rotational symmetry. It is also called radial symmetry.

From the above figure, we can observe the rotational symmetry. If you rotate the hexagonal object or image in a 60° clockwise direction with respect to the origin, there is no change in the shape of an image. More Examples for Rotational Symmetry are Circle, Hexagonal, Square, Rectangle, and etc…

3.Reflexive Symmetry

Reflexive Symmetry is the same as a line of symmetry. Yes, in this type of symmetry one part of the image or object represents the mirror image of another part of the image. Reflexive Symmetry is also called a line of symmetry or mirror symmetry. The below figure is a better example of Reflexive symmetry.

The above object is divide into two parts and the left side part is the mirror image of the right side of the image.

4.Glide Symmetry

It is the combination of both translation symmetry and reflection symmetry.

Point Symmetry

When an object is in opposite direction, every part of the object must be matched with the original object. It is called Point Symmetry. It is the same as Rotational Symmetry, so we can call it Rotational Symmetry order 2.

Solved Examples on Types of Symmetry

1. Name and draw the shape which possesses linear symmetry, point symmetry, and rotational symmetry?

Solution:
(i) Line Segment

Linear symmetry is a line of symmetry. here, it indicates ‘AB’.
Point symmetry, the mid-point of the line of origin of the image that is ‘O’.
Rotational Symmetry, If we move the above image in any direction with respect to the origin, there is no change in the image. Here, the origin of the image is ‘O’

(ii) Square

Linear symmetry, two lines of symmetry.
Point symmetry, the intersection of two lines that is ‘O’.
Rotational Symmetry order of 2.

2. If the following figure shows a line of symmetry, then complete the figure?

Solution:
The line of symmetry, vertical or horizontal line divides the image into two equal halves and two parts are look as same. So, the remaining part of the image also the same as the above figure. That is,

3. Identify which of the following figure is the example for symmetry?

Solution:
In the symmetry method, an image or object is divided into equal halves either it may be vertical lines or horizontal lines. Each part must be a mirror image of the other part of the image. That particular image, we can consider as the example for symmetry. In the above diagrams, figure ‘c’ is showing as an example of symmetry. In that one only, the image is divided into two equal halves and the remaining A and B are not divided into equal halves.

4. How many lines of symmetry does a rectangle have?

Solution:
Four lines of symmetry. One horizontal line, one vertical line, and two diagonal lines.

5. Identify which of the following image indicates the rotational symmetry?

Solution:
By moving in a forward or backward direction, an object or image will be in the same as the original image, which is called rotational symmetry. From the above, Figure (A) is the best example for Rotational symmetry.

FAQs on Types of Symmetry

1. What is Symmetry?

In symmetry, an object is divided into equal parts and each part of an object is a mirror image of another part of the object.

2. What are the Types of Symmetry?

There are four types of symmetry. They are

Translational Symmetry
Rotational Symmetry
Reflexive Symmetry
Glide Symmetry

3. What is a Line of Symmetry?

An object or image is divided into equal halves with horizontal or vertical or diagonal lines. But the left side of the image is the same as the right side of the image that is called a line of symmetry.

4. What is Point Symmetry?

If we place the image or object in the opposite direction, then every part of the image must be matched with the equal distance that is called point symmetry.

5. What is Asymmetric?

An object is divided into equal parts but the left side of the image is not the same as the right side of the image and it is called an asymmetric method.

Common Solid Figures – Definition, Shapes, Formulas, Properties, Examples

April 1, 2022March 22, 2021 by Prasanna

Solid shapes or figures are solids having 3 dimensions, namely length, breadth, and height. Solid figures are classified into different categories. The characteristics and properties of solid shapes, the number of faces, edges, and also the number of vertices are explained below. Also, we have given examples for a better understanding of solid shapes. Also, we have given the solid shapes with clear explanations. Check out the complete concept to learn about solid shapes.

Attributes of Solid Figures

Face: The flat surface present on the solid figure is known as the Face of the solid figure.
Edge: The edge of the solid figure is defined as the line where two faces meet.
Corner: The corner is a point where three or more edges join together is known as a corner.

Different Types of Solid Figures

There are different types of solid figures available in geometry. Check out the detailed explanation of some of the examples of solid figures below.

Cube

The first and important solid figure everyone discusses Cube. A cube is defined as a slid box-shaped that has six identical square faces. One solid figure that called a cube must consist of 6 equal and plane surfaces they appear as a square in shape.

A cube consists of 6 plane surfaces, 8 vertices and, 12 edges. There are two adjoining planes available in a cube which are called surfaces that meet at an edge. Also, it consists of 12 edges that are equal in length. These edges are straight edges. Furthermore, the joining point of two corners called a vertex. In a cube, there are 8 such vertices available.

Parts of a Cube

(i) Face: The sides of a cube are known as the Face of the cube. A cube consists of six faces. All the faces of a cube are square in shapes. Each face of a cube has four equal sides.
(ii) Edge: When two edges join each other with a line segment, then that corner is called the edge. The cube has 12 edges. All the 12 edges are equal in length as all faces are squares. These edges are straight edges.
(iii) Vertex: A point formed with the joint of the three edges is known as a vertex of a cube. There are 8 vertices in a cube.
(iv) Face Diagonals: Face Diagonals of a cube is the line segment that joins the opposite vertices of a face. There are 12 diagonals in the cube that are formed with 2 diagonals in each face altogether.
(v) Space Diagonals: Space diagonals of a cube are the line segment that joins the opposite vertices of a cube and also cutting through its interior. There are 4 space diagonals in a cube.

Properties of a Cube

Volume: The volume of a cube is shown by s³ where s is the length of one edge.
Surface Area: The surface area of a cube is 6s², where s is the length of one edge.

Also, Read:

Cuboid

The cuboid consists of 6 rectangular faces which form a convex polyhedron. The opposite rectangular plane surfaces are equal. It has 8 vertices and 12 edges.

A cuboid consists of 6 rectangular plane surfaces. There are 8 vertices and 12 edges. All the faces of a cuboid are equal and square. Therefore, a cube has all the six faces equal, whereas a cuboid has the opposite faces equal.

Properties of a Cuboid

Volume: The volume of a cuboid is lwh, where l is the length, h is the height, and w is the width.
Lateral Surface Area: The lateral surface area of a cuboid is 2lh + 2wh, where l is the length, w is the width, and h is the height.
Surface Area: The surface area of a cuboid is 2lw + 2lh + 2wh, where l is the length, w is the width and h is the height.

Cylinder

The cylinder is one of the basic 3d shapes that stands on a circular plane surface consisting of circular plane surfaces on its top and bottom. A cylinder has two circular plane surfaces. One surface presents at its base and the other one presents at its top. Also, it has a curved surface in the middle. Two edges at which the two plane surfaces meet with the curved surface present on a cylinder. The edges are curved in a shape.

A cylinder has 2 plane surfaces and 1 curved surface. There are 2 edges and no vertices. Furthermore, the top and bottom of the cylinder are of the same shape as well as in size. They both are equal.

Cone

A cone is a distinctive three-dimensional geometric figure that has one plane circular surface. It consists of a base and only one curved surface. There are 1 edge and 1 vertex present in the cone. The edge of the cone is a curved edge. It is formed by the circular plane surface meeting with the curved surface.

Sphere

A sphere is a geometrical figure that has a ball-like shape. There is only one curve surface present in the sphere and no edge and no vertex present in it.