Common Core Math

Depending upon the length and angles, quadrilaterals are classifieds in different ways. Let us check Different Types of Quadrilaterals and their definition, properties along with their diagrams. A quadrilateral can be explained using the below properties

• The sum of the interior angles is 360 degrees in a quadrilateral.
• A quadrilateral consists of 4 sides and 4 vertices, and also 4 angles.
• The sum of the interior angle from the formula of the polygon using (n – 2) × 180 where n is equal to the number of sides of the polygon.

The main types in a quadrilateral are squares and rectangles, etc., with the same angles and sides.

Various Types of Quadrilaterals

Mainly quadrilaterals are classified into six types. They are

1. Parallelogram
2. Rhombus
3. Rectangle
4. Square
5. Trapezium
6. Kite

Parallelogram

A quadrilateral is said to be a parallelogram when it has two pairs of parallel sides and opposite sides are parallel and equal in length. Also, the opposite angles are equal in a parallelogram. Let us take a parallelogram PQRS, then the side PQ is parallel to the side RS. Also, the side PS is parallel to a side QR.

Two diagonals are present in the parallelogram and they intersect each other at a midpoint. From the figure, PR and QS are two diagonals. Also, the diagonals are equal in length from the midpoint.

PQ ∥ RS and PS ∥ QR.

Rhombus

Rhombus is a quadrilateral when all the four sides of a quadrilateral having equal lengths. In a rhombus, opposite sides are parallel and opposite angles are equal.

From the above figure, PQRS is a rhombus in which PQ ∥ RS, PS ∥ QR, and PQ = QR = RS = SP.

Rectangle

A quadrilateral is considered as a rectangle when all 4 angles of it are equal and each angle is 90 degrees. Also, both pairs of opposite sides of a rectangle are parallel and have equal lengths.

From the above figure, PQRS is a quadrilateral in which PQ ∥ RS, PS ∥ QR and ∠P = ∠Q = ∠R = ∠S = 90°.

So, PQRS is a rectangle.

Square

A square is a quadrilateral consists all the sides and angles are equal. Also, every angle of a square is 90 degrees. The pairs of opposite sides of a square are parallel to each other.

From the above figure, PQRS is a quadrilateral in which PQ ∥ RS, PS ∥ QR, PQ = QR = RS = SP and ∠P = ∠Q = ∠R = ∠S = 90°.

So, PQRS is a square.

Trapezium

A quadrilateral is called a trapezium when it has one pair of opposite parallel sides.

From the above figure, PQRS is a quadrilateral in which PQ ∥ RS. So, PQRS is a trapezium. A trapezium its non-parallel sides are equal is called an isosceles trapezium.

Kite

A quadrilateral is said to be a kite that has two pairs of equal-length sides and the sides are adjacent to each other.

From the above figure, PQRS is a quadrilateral. PQ = PS, QR = RS, PS ≠ QR, and PQ ≠ RS.

So, PQRS is a kite.

Important Points to Remember for Quadrilaterals

Look at some of the important points need to remember about a quadrilateral.

• A square is a rectangle and also it becomes a rhombus.
• The rectangle and rhombus do not become a square.
• A parallelogram is a trapezium.
• Square, rectangle, and rhombus are types of parallelograms.
• A trapezium is not a parallelogram.
• Kite is not a parallelogram.

Parallelogram consists of a flat shape that has two opposite & parallel sides with equal length. The parallelogram has four sides and also it is called a quadrilateral. The pair of parallel sides are always equal in length of a parallelogram. Furthermore, the interior opposite angles also equal in measurement. While adding the adjacent angles of a parallelogram, you will get 180 degrees.

The area of the parallelogram always depends on its base and height. Also, the perimeter of the parallelogram depends on the length of its four sides.

List of Parallelogram Concepts

Have a glance at the list of Parallelogram Concepts available below and use them for your reference. All you need to do is simply tap on the quick links and avail the underlying concept within. Practice as much as you can and solve all the problems easily.

• Properties of a Rectangle Rhombus and Square
• Problems on Parallelogram
• Practice Test on Parallelogram

Parallelogram Definition

A parallelogram called a quadrilateral that has two pairs of parallel sides. The interior angles of the parallelogram on the same side of the transversal are supplementary. The sum of all the interior angles becomes 360 degrees in a parallelogram.

A rectangle and square also consist of similar properties of a parallelogram. If in case, the sides of the parallelogram become equal, then it treats as a rhombus. Or else, if a parallelogram has one parallel side and the other two sides are non-parallel, then it treats as a trapezium.

From the above figure, ABCD is a parallelogram, where CD || AB and BC || AD. Also, CD = AB and BC = AD.
And, ∠A = ∠C & ∠B = ∠D
Also, ∠A & ∠D are supplementary angles. Because ∠A & ∠D are interior angles present on the same side of the transversal. Similarly, ∠B & ∠C are supplementary angles.

Therefore, ∠B + ∠C = 180, ∠A + ∠D = 180.

Shape of Parallelogram

A parallelogram shape is a two-dimensional shape. It consists of four sides and two pairs of parallel sides. All the parallel sides of the Parallelogram are equal in length. Also, the interior angles of the parallelogram should always equal.

Angles of Parallelogram

The Parallelogram has four angles. Its opposite interior angles always equal and the angles on the same side of the transversal are always supplementary with each other. When you add the same side of the transversal angles, you can get 180 degrees. Furthermore, the sum of the interior angles is 360 degrees.

Properties of Parallelogram

Check the below properties of a parallelogram and solve the related problems easily by applying the same. They are as follows

• The opposite angles of a parallelogram are congruent.
• Also, the opposite sides are parallel and congruent
• The consecutive angles are supplementary
• Furthermore, The two diagonals bisect each other
• If one angle of a parallelogram is a right angle, then all other angles are right angles.
• Parallelogram law: The sum of squares of all the sides of a parallelogram is always equal to the sum of squares of its diagonals.
• Each diagonal bisects the parallelogram into two congruent triangles.

Area of Parallelogram

The area of the Parallelogram totally depends on the Base and height of the Parallelogram.
The area of the Parallelogram can be calculated as Area = Base × Height

Perimeter of Parallelogram

The perimeter of a parallelogram is calculated as the total distance of the boundaries of the parallelogram. By knowing the length and breadth of the parallelogram, we can get the perimeter of a parallelogram.

Perimeter = 2 (a+b) units where a and b are the length of the sides of the parallelogram.

Types of Parallelogram

Depends on the angles and sides of the Parallelogram, mainly four types of Parallelogram are considered.
Let ABCD is a Parallelogram,
1. If AB = BC = CD = DA are equal, then it is called a rhombus. The properties of the rhombus and parallelogram are equal.
2. Rectangle, Square are also types of the parallelogram.

Parallelogram Theorems

Theorem: Prove that in a parallelogram, the opposite sides are equal; the opposite angles are equal; diagonals bisect each other.

Proof:
Let ABCD be a parallelogram. Draw its diagonal AC.
In ∆ ABC and ∆ ACD, ∠1 = ∠4 (alternate angles)
∠3 = ∠2 (alternate angles)
and AC = CA (common)

Therefore, ∆ ABC ≅ ∆ ACD (by ASA congruence)
⇒ AB = CD, BC = AD and ∠B = ∠D.
Similarly, by drawing the diagonal BD, we can prove that
∆ ABD ≅ ∆ BCD
Therefore, ∠A = ∠C
Thus, AB = CD, BC = AD, ∠A = ∠C and ∠B = ∠D.
This proves (i) and (ii)
In order to prove (iii) consider parallelogram ABCD and draw its diagonals AC and BD, intersecting each other at O.
In ∆ OAB and ∆ OCD, we have
AB = CD [Opposite sides of a parallelogram]
∠AOB = ∠ COD [Vertically opposite angles]
∠OAB = ∠OCD [Alternate angles]
Therefore, ∆ OAB ≅ ∆ OCD [By ASA property]
⇒ OA = OC and OB = OD.
This shows that the diagonals of a parallelogram bisect each other.

Therefore, in a parallelogram, the opposite sides are equal; diagonals bisect each other; the opposite angles are equal.

Problems on Parallelogram are given in this article along with an explanation. It is easy to learn and understand the entire concept of a Parallelogram by solving every problem over here. There are various types of problems included according to the new updated syllabus. Get a good score in the exam and improve your preparation level immediately by working on your difficult topics.

1. Prove that any two adjacent angles of a parallelogram are supplementary?

Solution:
Let us take a parallelogram PQRS.

Then, PS ∥ QR and PQ is a transversal.
The sum of the interior angles on the same side of the transversal is 180°
Therefore, P + Q = 180°
Similarly, ∠R + ∠S = 180°, ∠Q + ∠R = 180°, and ∠S + ∠P = 180°.
Thus, the sum of any two adjacent angles of a parallelogram is 180°.

Hence, any two adjacent angles of a parallelogram are supplementary.

2. Two adjacent angles of a parallelogram PQRS are as 2 : 3. Find the measure of each of its angles?

Solution:
Let us take a parallelogram PQRS.

Then, ∠P and ∠Q are its adjacent angles.
Let ∠P = (2a)° and ∠Q = (3a)°.
The sum of adjacent angles of a parallelogram is 180°
Then, ∠P + ∠Q = 180°
⇒ 2a + 3a = 180
⇒ 5a = 180
⇒ a = 36.
Therefore, ∠P = (2 × 36)° = 72° and ∠Q = (3 × 36°) = 108°.
∠Q and ∠R are adjacent angles. By adding them, we get 180°
Also, ∠Q + ∠R = 180°
= 108° + ∠R = 180° [Since, ∠Q = 108°]
∠R = (180° – 108°) = 72°.
∠R and ∠S are adjacent angles and add up to 180°.
Also, ∠R + ∠S = 180°
⇒ 72° + ∠S = 180°
⇒ ∠S = (180° – 72°) 108°.

Therefore, ∠P = 72°, ∠Q = 108°, ∠R = 72°and ∠S = 108°.

3. In the adjoining figure, PQRS is a parallelogram in which ∠P = 75°. Find the measure of each of the angles ∠Q, ∠R, and ∠S.

Solution:
It is given that PQRS is a parallelogram in which ∠P = 75°.

Since the sum of any two adjacent angles of a parallelogram is 180°,
∠P + ∠Q = 180°
⇒ 75° + ∠Q = 180°
⇒∠Q = (180° – 75°) = 105°
∠Q and ∠R are adjacent angles and add up to 180º.
Also, ∠Q + ∠R = 180°
⇒ 105° + ∠R = 180°
⇒ ∠R = (180° – 105°) = 75°.
∠R and ∠S are adjacent angles
Further, ∠R + ∠S = 180°
⇒ 75° + ∠S = 180°
⇒ ∠S = (180° – 75°) = 105°.

Therefore, ∠Q = 105°, ∠R = 75° and ∠S = 105°.

4. In the adjoining figure, PQRS is a parallelogram in which ∠QPS = 75° and ∠SQR = 60°. Calculate:
(i) ∠RSQ and (ii) ∠PSQ.

Solution:
Let us draw a parallelogram PQRS.

We know that the opposite angles of a parallelogram are equal.
Therefore, ∠QRS = ∠QPS = 75°.
(i) Now, in ∆ QRS, we have
The sum of the angles of a triangle is 180°
∠RSQ + ∠SQR + ∠QRS = 180°
⇒ ∠RSQ + 60° + 75° = 180°
⇒ ∠RSQ + 135° = 180°
⇒ ∠RSQ = (180° – 135°) = 45°.
(ii) PS ∥ QR and QS are the transversals.
Therefore, ∠PSQ = ∠SQR = 60° [alternate interior angles]

Hence, ∠PSQ = 60°.

5. In the adjoining figure, PQRS is a parallelogram in which ∠RPS = 40°, ∠QPR = 35°, and ∠ROS = 65°.
Calculate: (i) ∠PQS (ii) ∠QSR (iii) ∠PRQ (iv) ∠RQS.

Solution:
(i) ∠POQ = ∠ROS = 65° (vertically opposite angles)
Now, from ∆OPQ, we can write as:
The sum of the angles of a triangle is 180°
∠OPQ + ∠PQO + ∠POQ =180°
⇒ 35°+ ∠PQO + 65° = 180°
⇒ ∠PQO + 100° = 180°
⇒ ∠PQO = (180° – 100°) = 80°
⇒ ∠PQS = ∠PQO = 80°.
(ii) PQ ∥ SR and QS is a transversal.
Therefore, ∠QSR = ∠PQS = 80° [alternate interior angles]
Hence, ∠QSR = 80°.
(iii) PS ∥ QR and PR is a transversal.
Therefore, ∠PRQ = ∠RPS = 40° [alternate interior angles]
Hence, ∠PRQ = 40°.
(iv) ∠QRS = ∠QPS = (35° + 40°) = 75° [opposite angles of a parallelogram]
Now, in ∆RQS, we have
The sum of the angles of a triangle is 180°.
∠QSR + ∠QRS + ∠RQS = 180°
⇒ 80° + 75° + ∠RQS = 180°
⇒ 155° + ∠RQS = 180°
⇒ ∠RQS = (180° – 155°) = 25°.
Hence, ∠RQS = 25°.

6. In the adjoining figure, PQRS is a parallelogram, PO and QO are the bisectors of ∠P and ∠Q respectively. Prove that ∠POQ = 90°.

Solution:
We know that the sum of two adjacent angles of a parallelogram is 180°
Therefore, ∠P + ∠Q = 180° ……………. (i)
Since PO and QO are the bisectors of ∠P and ∠Q, respectively, we have
∠OPQ = 1/2∠P and ∠PQO = 1/2∠Q.
From ∆OPQ, we have
The sum of the angles of a triangle is 180°
∠OPQ + ∠POQ + ∠PQO = 180°
⇒ ¹/₂∠P + ∠PQO + ¹/₂∠Q = 180°
⇒ ¹/₂(∠P + ∠Q) + ∠POQ = 180°
⇒ (¹/₂ × 180°) + ∠POQ = 180° [from equation (i)]
⇒ 90° + ∠POQ = 180°
⇒ ∠POQ = (180° – 90°) = 90°.

Hence, ∠POQ = 90°.

7. The ratio of two sides of a parallelogram is 5: 4. If its perimeter is 54 cm, find the lengths of its sides?

Solution:
Let the lengths of two sides of the parallelogram be 5a cm and 4a cm respectively.
Find the perimeter using given values.
Then, its perimeter = 2(5a + 4a) cm = 2 (9a) cm = 18a cm.
Therefore, 18a = 54 ⇔ a = 54/18 = 3.

Therefore, one side = (5 × 3) cm = 15 cm and other side = (4 × 3) cm = 12 cm.

8. The length of a rectangle is 16 cm and each of its diagonals measures 20 cm. Find its breadth?

Solution:
Let PQRS be the given rectangle in which length PQ = 16 cm and diagonal PR = 20 cm.

Since each angle of a rectangle is a right angle, we have
∠PQR = 90°.
From the right ∆PQR, we have
PQ² + QR² = PR² [From Pythagoras’ Theorem]
⇒ QR² = (PR² – PQ²) = {(20)² – (16)²} = (400 – 256) = 144

⇒ QR = √144 = 12 cm.

Hence, breadth = 12 cm.

9. In the below figure, PQRS is a rhombus whose diagonals PR and QS intersect at a point O. If side PQ = 20 cm and diagonal QS = 32 cm, find the length of diagonal PR.

Solution:
We know that the diagonals of a rhombus bisect each other at right angles.
Therefore, QO = ¹/₂QS = (¹/₂ × 32) cm = 16 cm, PQ = 20 cm and ∠POQ = 90°.
From right ∆OPQ, we have PQ² = PO² + QO²
⇒ PO² = (PQ² – QO²) = {(20) ² – (16)²} cm²
= (400 – 256) cm²
= 144 cm²
⇒ PO = √144 cm = 12 cm.

Therefore, PR = 2 × PO = (2 × 12) cm = 24 cm.

The quadrilateral is a figure formed by adding the four-line segments. It consists of 4 sides, 4 vertices, and two diagonals. By going through this entire article you will get a complete idea of Quadrilateral like Types, Sides, Angles, Vertices, Diagonals of it, its Properties etc. If P, Q, R, S are four points and where no three points are collinear and also the line segments PQ, QR, RS, and SP do not intersect at their endpoints. Check the below figure that is the quadrilateral PQRS.

In a quadrilateral PQRS
(i) The vertices in a quadrilateral are P, Q, R, S.
(ii) The sides of a quadrilateral are PQ, QR, RS, and SP.
(iii) Also, the angles of quadrilateral are ∠SPQ, ∠PQR, ∠QRS and ∠RSP.
(iv) The line segments are PQ and QS.

Convex Quadrilaterals and Concave Quadrilaterals

If each angle of a quadrilateral is less than 180°, then it is called a convex quadrilateral. Also, if one angle of the quadrilateral is more than 180°, then it is called a concave quadrilateral. A quadrilateral is not a simple closed figure.

Sides, Angles, Vertices, Diagonals of the Quadrilateral

Have a look at the complete details of a Quadrilateral below.

Adjacent Sides of a Quadrilateral

Adjacent Sides of a Quadrilateral are nothing but the sides that have a common endpoint. If PQRS is a Quadrilateral, then (PQ, QR), (QR, RS), (RS, SP), and (SP, PQ) are four pairs of adjacent sides of quadrilateral PQRS.

Opposite Sides of a Quadrilateral

In a given quadrilateral, the two sides are said to be opposite sides when they do not have a common endpoint. If PQRS is a quadrilateral, then (PQ, SR) and (PS, QR) are two pairs of opposite sides of quadrilateral PQRS.

Adjacent Angles of a Quadrilateral

An angle is formed when two rays meeting at a common endpoint. Two angles of a quadrilateral are said to be adjacent when they have a common arm. From the given figure, (∠P, ∠Q), (∠Q, ∠R), (∠R, ∠S), and (∠S, ∠P) are four pairs of adjacent angles of quadrilateral PQRS.

Opposite Angles of a Quadrilateral

Opposite Angles of a Quadrilateral are not adjacent angles. If you consider a quadrilateral PQRS, then (∠P, ∠R) and (∠Q, ∠S) are two pairs of opposite angles of quadrilateral PQRS.

Adjacent Vertices of a Quadrilateral

In a Quadrilateral, if two vertices have a common side are known as adjacent vertices. From the figure, the pairs of adjacent vertices are (P, Q); (Q, R); (R, S), and (S, P).

Opposite Vertices of a Quadrilateral

Opposite Vertices of a Quadrilateral are vertices that do not have a common side. From the figure, the pairs of opposite vertices are (P, R) and (Q, S).

Diagonal of a Quadrilateral

When a line segment of the opposite vertices of a quadrilateral is joined, then the diagonal of the quadrilateral is formed. From the given figure, the two diagonals are PR and QS.

Properties of a Rectangle Rhombus and Square is always a confusing concept for students. Learning every individual topic is important to score good marks in the exam. So, we have explained every individual topic clearly in a detailed manner in this article. Therefore, those who wish to learn the concepts of Parallelogram and its properties, problems, can completely learn the Parallelogram concepts on our website.

Rectangle

A rectangle is said to be a parallelogram when it has all 4 angles having equal measure.

Properties of Rectangle

• The Opposite sides of a rectangle are parallel.
• Also, the Opposite sides of a rectangle are equal in length.
• Diagonals are equal in length.
• The interior angles are 90 degrees each.
• Diagonals bisect each other.
• It has horizontal and vertical lines of symmetry.
• Each of the diagonal bisects the rectangle into 2 congruent triangles.
• If you combine the 4 sides of a rectangle, then the mid-points of it form a rhombus.

Rectangle Formulas

If l is the length of the rectangle and b is the breadth of the rectangle, then
Area = lb square units
Perimeter = 2 (l+b) units.

Diagonal Properties of a Rectangle

Prove that the diagonals of a rectangle are equal and bisect each other.

Proof:
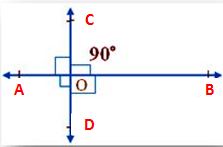
Let PQRS be a rectangle that has diagonals PQ and QS intersect at the point O.

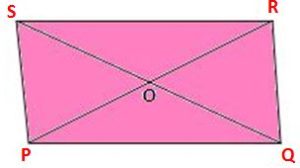
From ∆ PQR and ∆ QPS,
PQ = QP (common)
∠PQR = ∠QPS (each equal to 90º)
QR = PS (opposite sides of a rectangle).
Therefore, ∆ PQR ≅ ∆ QPS (by SAS congruence)
⇒ PR = QS.
Hence, the diagonals of a rectangle are equal.
From ∆ OPQ and ∆ ORS,
∠OPQ = ∠ORS (alternate angles)
∠OQP = ∠OSR (alternate angles)
PQ = RS (opposite sides of a rectangle)
Therefore, ∆OPQ ≅ ∆ ORS. (by ASA congruence)
⇒ OP = OR and OQ = OS.
This shows that the diagonals of a rectangle bisect each other.

Hence, the diagonals of a rectangle are equal and bisect each other.

Rhombus

The rhombus is a quadrilateral that consists of four sides with equal lengths.

Properties of Rhombus

• The Rhombus consists of parallel and equal opposite sides. As it consists of parallel and equal opposite sides, it is said to be a parallelogram.
• All available sides (4 sides) are equal.
• Also, opposite angles in a rhombus are equal.
• Diagonals bisect each other.
• Diagonals of a rhombus intersect each other at right angles.
• Furthermore, Diagonals bisect opposite vertex angles.
• Every diagonal divides the rhombus into 2 congruent triangles.

Rhombus Formula

If b is the side, a and b are the two diagonals of the rhombus, then
Area = ab/2 Square units.
Perimeter = 4b units

Diagonal Properties of a Rhombus

Prove that the diagonals of a rhombus bisect each other at right angles.

Proof:
Let PQRS be a rhombus whose diagonals AC and BD intersect at point O.

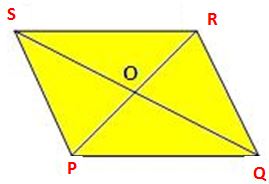
The diagonals of a parallelogram bisect each other. Also, we know that every rhombus is a parallelogram.
So, the diagonals of a rhombus bisect each other.
Therefore, OP = OR and OQ = OS
From ∆ ROQ and ∆ ROS,
RQ = RS (sides of a rhombus)
RO = RO (common).
OQ = OS (proved)
Therefore, ∆ ROQ ≅ ∆ ROS (by SSS congruence)
⇒ ∠ROQ = ∠ROS
But, ∠ROQ + ∠ROS = 2 right angles (linear pair)
Therefore, ∠ROQ = ∠ROS = 1 right angle.

Hence, the diagonals of a rhombus bisect each other at right angles.

Square

A square is a rectangle that has all equal sides.

Properties of Square

• The opposite sides of a square are parallel.
• All 4 sides are equal in length.
• Diagonals are equal in length.
• Diagonals bisect opposite vertex angles.
• The interior angles of a square measure 90 degrees each.
• Diagonals bisect each other at right angles.
• It has 4 lines of symmetry – a horizontal, a vertical, and 2 diagonals.
• Each diagonal bisects the square into 2 congruent triangles.

Square Formula

If b is the side of the square, then
Area = b² square units
Perimeter = 4b units.

Diagonal Properties of a Square

Prove that the diagonals of a square are equal and bisect each other at right angles.

Proof:
We know that the diagonals of a rectangle are equal.
Also, every square is a rectangle.
Therefore, the diagonals of a square are equal.
Again, the diagonals of a rhombus bisect each other at right angles. But, every square is a rhombus.
So, the diagonals of a square bisect each other at right angles.

Hence, the diagonals of a square are equal and also bisect each other at right angles.

Note 1: If the diagonals of a quadrilateral are equal but it is not necessary to be a rectangle.
Note 2: If the diagonals of a quadrilateral interest at a point with right angles then also it is not necessary to become a rhombus.

Construction Of Quadrilaterals is easy if you have a complete grip on the concept. A quadrilateral is a polygon with 4 sides, 4 angles, and also 4 vertices. When you add the interior angles of a quadrilateral, then you can get 360 degrees. The quadrilateral side lengths and angles may different. Depending on the lengths and angles of the sides, you can easily know what is the name of the quadrilateral. You can easily construct a quadrilateral by considering the following criteria.

(i) 4 sides and 1 diagonal is given.
(ii) 3 sides and including 2 angles are given
(iii) 2 sides and three angles are given
(iv) 3 sided and 2 diagonals are given
(v) 4 sides and 1 angle is given

1. Construct the Quadrilateral when 4 sides and 1 diagonal is given
PQ = 5 cm
QR = 4.5 cm
RS = 3.8 cm
PS = 4.4 cm
Diagonal PQ = 6 cm

Steps of Construction:
Firstly, draw a rough figure of the quadrilateral with the given dimensions.

1. Draw a line segment of length 5 cm and mark the ends as P and Q.
2. Take the point P as a center and draw an arc by taking the radius 6 cm.
3. Next, take point Q as a center and draw an arc by taking the radius 4.5 cm. Mark the point as R where the two arcs cross each other. Join the points Q and R as well as P and R.
4. By taking the point P as a center, draw an arc with a radius of 4.4 cm.
5. By taking the point R as a center, draw an arc with a radius of 3.8 cm.
6. Mark the point as S where the two arcs cross each other. Join the points R and S as well as P and S.

The final result is the required quadrilateral.

2. Construct the Quadrilateral when 3 sides and including 2 angles are given
PQ = 3.8 cm
QR = 4.2 cm
PS = 5.2 cm
∠QPS = 180º
∠PQR = 80º

Steps of Construction:
Firstly, draw a rough figure of the quadrilateral with the given dimensions.

1. Draw a line segment of length 3.8 cm and mark the ends as P and Q.
2. Take point P as a center and make a point by taking 180º using a protector.
3. Next, take point P as a center and draw an arc by taking the radius 5.2 cm. Mark the point as S where the point and arc cross each other. Join the points P and S.
4. By taking the point Q as a center, make a point by taking 80º using a protector.
5. By taking the point Q as a center, draw an arc with a radius of 4.2 cm.
6. Mark the point as R where the point and arc cross each other. Join the points Q and R.
7. Finally, join the points R and S and draw a line segment.

The final result is the required quadrilateral.

3. Construct the Quadrilateral when 3 sides and including 2 angles are given
AB = 4.7 cm
∠ABC = 120°,
BC = 4 cm,
∠BCD = 100°, and ∠BAD = 60°.

Steps of Construction:
Firstly, draw a rough figure of the quadrilateral with the given dimensions.

1. Draw a line segment of length 4.7 cm and mark the ends as A and B.
2. Take point A as a center and make a point by taking 60º using a protector.
3. Next, take point B as a center and make a point by taking 120º using a protector. Mark the point as D where the two points are meet at a point. Join the points A and D.
4. By taking the point B as a center, draw an arc with a radius of 4 cm.
5. Mark the point as C where the point and arc cross each other. Join the points B and C.
6. Finally, join the points C and D and draw a line segment.

The final result is the required quadrilateral.

4. Construct the Quadrilateral when 3 sided and 2 diagonals are given
PQ = 4.2 cm
QR = 4 cm
PS = 3.2 cm
Diagonal PR = 5 cm
Diagonal QS = 4.6 cm

Steps of Construction:
Firstly, draw a rough figure of the quadrilateral with the given dimensions.

1. Draw a line segment of length 4.2 cm and mark the ends as P and Q.
2. Take the point P as a center and draw an arc by taking the radius 5 cm.
3. Next, take point Q as a center and draw an arc by taking the radius 4 cm. Mark the point as R where the two arcs cross each other. Join the points Q and R as well as P and R.
4. By taking the point P as a center, draw an arc with a radius of 3.2 cm.
5. By taking the point Q as a center, draw an arc with a radius of 4.6 cm.
6. Mark the point as S where the two arcs cross each other. Join the points R and S as well as P and S.

The final result is the required quadrilateral.

5. Construct the Quadrilateral when 4 sides and 1 angle is given.
PQ = 4 cm, QR = 3.6 cm, RS = 4.7 cm, PS = 5.2 cm and ∠B = 80°.

Steps of Construction:
Firstly, draw a rough figure of the quadrilateral with the given dimensions.

1. Draw a line segment of length 4 cm and mark the ends as P and Q.
2. Take point Q as a center and make a point by taking 80º using a protector.
3. Next, take point Q as a center and draw an arc with a radius of 3.6 cm. Mark the point as R where the two points are meet at a point. Join the points Q and R.
4. By taking the point P as a center, draw an arc with a radius of 5.2 cm.
5. By taking the point R as a center, draw an arc with a radius of 4.7 cm.
6. Mark the point as S where the two arcs cross each other. Join the points P and S, R and S.

The final result is the required quadrilateral.

A Transversal Line is a line that crosses at least two lines (Parallel Lines) and intersects with them. Find Problems on Transversal Lines with Solutions for a better understanding of the concept. Check concept and examples of Lines and Angles on our website for free.

From the above figure, A and B are parallel lines and line C is intersecting both lines at points D and E. The line C is called as Transversal Line.

From the above figure, The line M intersecting Lines N and O at a point c. But the Lines N and O are not parallel lines. Therefore, Line M is not a Transversal Line.

Angles made by the Transversal with Two Lines

From the above figure, Line C intersecting Line A and B (parallel lines). The angles formed around the Transversal line are called Transversal angles. From the given figure, ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7, ∠8 are the angles with special names.

Interior Angles

The angles that present in the area enclosed between two parallel lines and that are intersected by a transversal are also called interior angles. From figure, ∠3, ∠4, ∠5, ∠6 are interior angles.

Exterior Angles

The angles that present outside two parallel lines and that are intersected by a transversal are called Exterior angles. From the figure, ∠1, ∠2, ∠7, ∠8 are Exterior angles.

Corresponding Pair of Angles

The corresponding pair of angles present on the same side of the transversal. In the Pair of corresponding angles, if one is an interior angle, the other will be an exterior angle. Also, they do not form a linear pair. From the figure, (∠2, ∠6); (∠1, ∠5); (∠3, ∠7); (∠4, ∠8) are the Corresponding pair of angles.

Pair of Alternate Angles

Pair of alternate angles present on the opposite sided of the transversal. Both Pair of Alternate Angles either interior angles or both are exterior angles. They will not form a linear pair. From the figure, (∠4, ∠6) and (∠3, ∠5) are interior alternate angles. Also, (∠1, ∠7) and (∠2, ∠8) are exterior alternate angles.

Pair of Co-interior or Conjoined or Allied Angles

Pair of co-interior or Conjoined or Allied Angles are pairs of interior angles that present on the same side on the transversal. From the figure, (∠3, ∠6); (∠4, ∠5) are co-interior angles.

Two Parallel Lines are cut by the Transversal

When two parallel lines A and B are intersected by a Transversal line C, then

• the pairs of alternate angles are equal ∠4 = ∠6, ∠ 1 = ∠7, ∠3 =∠5, ∠2 = ∠8.
• the pairs of corresponding angles are equal ∠2 = ∠6, ∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8.
• Interior angles on the same side of transversal are supplementary ∠4 + ∠ 5 = 180°, ∠6 = 180°.

Converse

When two parallel lines are intersected by a Transversal line

• pairs of alternate angles are equal
• pairs of corresponding angles are equal
• interior angles on the same side of the transversal are supplementary.

Parallel Lines are two lines in a plane, they do not intersect and parallel to each other. The distance between the parallel lines is always the same. The symbol to denote parallel lines is ||. Learn and practice all Lines and Angles concepts and problems on our website.

From the above figure, Line A and Line B are parallel lines. We can write it as A || B and we can read it as A is parallel to B.

Properties Of Angles Associated with Parallel Lines

From the above figure, A and B are two parallel lines and C is passing through two parallel lines by intersecting them at a point. C is a transversal line. If a line intersects two or more lines at distinct points then it is known as a transversal line. When two lines meet at a point in a plane, they are known as intersecting lines.

• The pair of corresponding angles is equal (∠4 = ∠8); (∠3 = ∠7); (∠2 = ∠6); (∠1 = ∠5).
• The pair of exterior alternate angles is equal (∠2 = ∠8); (∠1 = ∠7).
• The pair of interior alternate angles is equal (∠3 = ∠5); (∠4 = ∠6).
• Interior angles present on the same side of the transversal are supplementary, i.e., ∠4 + ∠5 = 180° and ∠3 + ∠6 = 180°.

Example:

Look at the above figure and check out the parallel lines, transversal line, and etc.,
From the above figure, AB and CD are parallel lines and MN is a transversal line that cuts the parallel lines AB and CD.
(i) Interior and exterior alternate angles are equal.
i.e. ∠4 = ∠5 and ∠3 = ∠6 [Interior alternate angles]
∠2 = ∠7 and ∠1 = ∠8 [Exterior alternate angles]
(ii) Corresponding angles are equal.
i.e. ∠2 = ∠6; ∠1 = ∠5; ∠3 = ∠7 and ∠4 = ∠8
(iii) Co-interior or allied angles are supplementary.
i.e. ∠4 + ∠6 = 180° and ∠3 + ∠5 = 180°

Conditions of Parallelism

Two straight lines are cut by a transversal, and if

• the two pairs of corresponding angles are equal and also the lines are parallel to each other.
• if the pair of interior angles on the same side of the transversal are supplementary, then the two straight lines are parallel.
• the pair of alternate angles are equal, then the straight lines are parallel to each other.

Parallel Rays

Parallel Rays are two rays that do not intersect each other and have the same distance every time. A ray consists of one endpoint. If AB and CD are two rays and parallel rays, then it is represented as ray AB ∥ ray CD.

Parallel Segments

If two line segments are parallel then those two line segments are called Parallel Segments. The line segment is a line that consists of two endpoints. If AB and CD are two line segments and parallel, then it is represented as line segment AB ∥ line segment CD.

Learn what are Vertically Opposite Angles and how to calculate them in this article. Vertically Opposite Angles are the angles formed when two lines intersect each other. The vertically opposite angles are always equal to each other. The adjacent angles of vertically opposite angles are always supplementary angles and they form 180º when we add them. Find Lines and Angles concepts and problems on our website.

If one angle is 35º, then the other angle is 180º – 35º.

From the above figure, the line segment PQ and RS meet at the point O and these two lines are intersecting lines.

In a pair of intersecting lines, the angles which are opposite to each other form a pair of vertically opposite angles. From the figure, ∠SOQ and ∠POR form a pair of vertically opposite angles.

∠SOQ = ∠POR
∠SOP = ∠ROQ

Note: A vertical angle and its adjacent angle is supplementary to each other. It means they add up to 180 degrees.

Vertical Angles Theorem and Proof

Theorem: In a pair of intersecting lines the vertically opposite angles are equal.

Proof: Consider two lines PQ and RS which intersect each other at O. The two pairs of vertical angles are:
i) ∠SOQ = ∠POR
ii) ∠SOP = ∠ROQ

It can be seen that ray OS stands on the line PQ and according to Linear Pair Axiom, if a ray stands on a line, then the adjacent angles form a linear pair of angles.
Therefore, ∠SOQ + ∠SOP = 180° —(1) (Linear pair of angles)
Similarly, Ray OP stands on the line SR.
Therefore, ∠SOP + ∠POR = 180° —(2) (Linear pair of angles)
From (1) and (2),
∠SOQ + ∠SOP = ∠SOP + ∠POR
⇒ ∠SOQ = ∠POR —(3)
Also, OQ stands on the line SR.
Therefore, ∠SOQ + ∠QOR = 180° —(4) (Linear pair of angles)
From (1) and (4),
∠SOQ + ∠SOP = ∠SOQ + ∠QOR
⇒ ∠SOP = ∠QOR —(5)
Thus, the pair of opposite angles are equal.

Hence, proved.

Vertically Opposite Angles Examples

1. In the given figure, find the measure of unknown angles.

Solution:
From the given figure
(i) ∠C = 60° vertically opposite angles
(ii) ∠B = 90° vertically opposite angles
(iii) ∠B + ∠A + 60° = 180° (straight angle)
90° + ∠ A + 60° = 180°
150° + ∠ A = 180°
Therefore, ∠A = 180° – 150° = 30°
(iv) ∠A = ∠D vertically opposite angles

Therefore, ∠D = 30°

2. In the given figure, lines AB, CD, EF intersects at O. If M : N : P = 1 : 2 : 3, then find the values of M, N, P.

Solution:
We know that the sum of all the angles at a point is 360°.
∠AOC = ∠DOB = M° (Pair of vertically opposite angles are equal.)
∠FOB = ∠AOE = N° (Pair of vertically opposite angles are equal.)
∠EOD = ∠COF = P° (Pair of vertically opposite angles are equal.)
Therefore, ∠AOE + ∠AOC + ∠COF + ∠FOB + ∠BOD + ∠DOE = 360°
N + M + P + N + M + P = 360°
⟹ 2M + 2N + 2P = 360°
⟹ 2(M + N + P) = 360°
⟹ M + N + P = 3̶6̶0̶°/2̶
⟹ M + N + P = 180° ——— (i)
Let the common ratio be a.
Therefore, M = a, N = 2a, P = 3a
Therefore, from the equation (i) we get;
a + 2a + 3a = 180°
⟹ 6a = 180°
⟹ a = 1̶8̶0̶°/6̶
⟹ a = 30°
Therefore, M = a, means M = 30°
N = 2a, means N = 2 × 30 = 60°
P = 3a, means P = 3 × 30 = 90°

Therefore, the measures of the angles are 30°, 60°, 90°.

Do you want to know What is linear pair of angles? Linear Pair of Angles are similar to adjacent angles but only the difference is adding two angles we get 180º in linear angles. Linear Pair of Angles will also have a common vertex, common arm like adjacent angles. Their interiors will also do not overlap. Remember that all adjacent angles may not form a linear pair. Learn all the Lines and Angles concepts in one place on our website.

Properties of Linear Pair of Angles

Check the below Linear Pair of Angles properties listed below.

• They have a common vertex.
• They have a common arm.
• Also, they do not overlap.
• The sum of the angles is 180°.

From the above figure, AO and OC are two opposite rays and ∠AOB and ∠BOC are the adjacent angles. Therefore, ∠AOB and ∠BOC form a linear pair.

Explanation for Linear Pair of Angles

The angle between the two straight lines is 180° and they form a straight angle. The line segment is the portion of a line that consists of two endpoints. Also, a line with one endpoint is known as a ray. If you consider a line mn and the middle point is o. A ray OP dividing the two lines MO and ON. The complete angle MOP and angle PON becomes 180º to form a linear pair of angles.

∠MOP + ∠PON = ∠MON = 180°

We have also given Lines and Angles concepts and problems for free of cost on our website.

Axioms

Axiom 1: If a ray stands on a line then the adjacent angles form a linear pair of angles.

From the above figure, there are different line segments available that are passing through point O. From the figure, we can say that Angle BOD and Angle BOC are Linear Pair of Angles.

Linear Pair of Angles Examples

In the given figure, ∠AOC and ∠ BOC form a linear pair if x – y = 50°, find the value of x and y.

Solution:
Given x – y = 50° ………… (i)
We know that, x + y = 180° ………… (ii)
Adding (i) and (ii)
x – y + x + y = 180° + 50°
2x = 230°
x = 240°/2
Therefore, x = 115°

Since, x – y = 50°
or, 115° – y = 50°
or, 115° – 115° – y = 50° – 115°
or, -y = -65°
Therefore, y = 65°

The final answer is x = 115° and y = 65°.

Adjacent Angles are the angles that have a common vertex and common arm. The other arms of the two adjacent angles present on the opposite sides of the common arm. The adjacent angles can be a supplementary angle or complementary angle when they share the common vertex and side. Find other concepts of Lines and Angles along with the adjacent angles on our website with a clear explanation.

From the above figure, YO is the common arm and Y is the common vertex. The above figure shows a pair of adjacent angles. The Ray XY and ray YZ are present on the opposite sides of the common arm YO. Therefore, ∠XYO and ∠OYZ are adjacent angles.

∠XYZ and ∠XYO are not adjacent angles, because their other arms YZ and YO are not on the opposite sides of the common arm XY.

Adjacent Angle Example

If you take a wall clock, you can see a minute hand, second hand, and also an hour hand. The minute hand and second hand of the clock form one angle represented as ∠XYO and the hour hand form another angle with the second hand represented as∠OYZ. Both the angles i.e.∠XYO and ∠OYZ are present on the opposite sides of the common hand. Therefore, these two angles are adjacent angles.

Properties of Adjacent Angles

Check out the Properties of Adjacent Angles mentioned below as a part of your preparation. They are as such

• Adjacent Angles share the common vertex
• Angles do not overlap
• They share the common arm
• There is no common interior-point in Adjacent Angles.
• It may be complementary or supplementary angles.
• There should be a non-common arm on both sides of the common arm.

Adjacent Angles Solved Problems

1. Are the following angles adjacent? Give reasons.

Solution:

(a) From figure a, ∠1, and ∠2 don’t have a common arm. Therefore, ∠1 and ∠2 are not adjacent angles.
(b) Adjacent angles will not overlap each other. From figure b, ∠1 and ∠2 interiors are overlapped. Therefore, ∠1 and ∠2 are not adjacent angles.
(c) Adjacent angles must have a common vertex. from figure c, ∠1, and ∠2 don’t have a common vertex. Therefore, ∠1 and ∠2 are not adjacent angles.
(d) From figure (d), ∠1 and ∠2 are adjacent angles. Because they have a common vertex, a common arm, and their interiors do not overlap.

Complementary and Supplementary Angles are the angles formed by adding two angles. If the sum of the two angles is 90º, they are called Complementary angles. Or else, if the sum of the two angles is 180º, they are called Supplementary angles. Find different problems on Supplementary and Complementary Angles in this article. Also, we have given all the concepts available in Lines and Angles on our website.

Complementary Angles

The two angles are said to be complementary angles if their sum is one right angle i.e. 90°. Each angle is called the complement of the other. If x° is one angle then (90 – x)° is the other angle in Complementary Angles.

For example, if 70° is one angle in Complementary Angles, then the other angle will be 20°. 70° and 20° complement each other.

Example 1: To find the complement of 3y + 52°, subtract the given angle from 90 degrees.
90º – (3y + 52º) = 90º – 3y – 52º = -3y + 38º

The complement of 3y + 52° is 38º – 3y.

Facts of complementary angles

• Two complementary angles are acute but vice versa is not possible
• Two right angles cannot complement each other
• Also, two obtuse angles cannot complement each other

Supplementary Angles

The two angles are said to be Supplementary angles if their sum is 180°. Two angles are added and formed a straight line in Supplementary Angles. If x is one angle then (180 – x)° is the other angle in Supplementary Angles.

For example, if 130° is one angle in Supplementary Angles, then the other angle will be 50°. By adding 130 and 50 degrees, it forms a straight line. In Supplementary Angles, both angles are said to be a supplement to each other.

Solved Examples on Supplementary and Complementary Angles

1. Find the complement of 50 degrees?

Solution:
The given angle is 50 degrees, then, the Complement is 40 degrees.
We know that Sum of Complementary angles = 90 degrees.
By adding 40 degrees to 50 degrees, the total angle becomes 90 degrees.
So, 50° + 40° = 90°

The final answer is 90°

2. Find the Supplement of the angle 1/4 of 200°.

Solution:
Given that the angle 1/4 of 200°
Convert 1/4 of 200°
That is, 1/4 x 200° = 50°
Supplement of 50° = 180° – 50° = 130°
By adding 130 degrees to 50 degrees, the total angle becomes 180 degrees.

Therefore, Supplement of the angle 1/4 of 200° is 130°

3. The measures of two angles are (x + 15)° and (3x + 25)°. Find the value of x if angles are supplementary angles.

Solution:
We know that, Sum of Supplementary angles = 180 degrees.
So, (x + 15)° + (3x + 25)° = 180°
Add the x terms and numbers.
4x + 40° = 180°
Move 40° to the right side and subtract it from 180°.
4x = 140°
Move 4 to the right side and divide it from 140°.
x = 35°

The value of x is 35 degrees.

4. The difference between two complementary angles is 54°. Find both the angles.

Solution:
Given that the difference between two complementary angles is 54°.
Let, the first angle = x degrees, then, Second angle = (90 – x)degrees {as per the definition of complementary angles}
Difference between angles = 54°
Now, (90° – x) – x = 54°
90° – 2x = 54°
– 2x = 54° – 90°
-2x = -36°
x = 36°/2°
x = 18°
Again, Second angle = 90° – 18° = 72°

Therefore, the required angles are 18°, 72°.

5. Find the complement of the angle 4/5 of 90°.

Solution:
Convert 4/5 of 90°
Multiply 4/5 with 90°
4/5 × 90° = 72°
Complement of 72° = 90° – 72° = 18°

Therefore, a complement of the angle 4/5 of 90° = 18°

6. Find the supplement of the angle 2/3 of 90°.

Solution:
Convert 2/3 of 90°
2/3 × 90° = 60°
Supplement of 60° = 180° – 60° = 120°

Therefore, a supplement of the angle 2/3 of 90° = 120°

7. The measure of two complementary angles are (3x – 6)° and (x – 4)°. Find the value of x.

Solution:
According to the problem, (3x – 6)° and (x – 4)°, are complementary angles’ so we get;
(3x – 6)° + (x – 4)° = 90°
or, 3x – 6° + x – 4° = 90°
or, 3x + x – 6° – 4° = 90°
or, 4x – 10° = 90°
Add 10° on both sides.
or, 4x – 10° + 10° = 90° + 10°
or, 4x = 100°
or, x = 100°/4°
or, x = 25°

Therefore, the value of x = 25°.

Supplementary angles are the angles that are added up to 180 degrees. If one angle is 120 degrees then the other angle is 60 degrees in supplementary angles because by adding 120 and 60, we get 180 degrees. By adding two supplementary angles, they form a straight line and a straight angle. One important thing in supplementary angles is the two angles need not be next to each other.

The important geometry concepts Lines and Angles are explained on our website with detailed explanations and solved examples. Learn all the concepts and improve your preparation level easily.

Supplementary Angle Definition

Supplementary Angle form 180º by adding two angles.

From the given figure, Angle AOC is one angle and angle BOC is another angle. By adding the two angles AOC and BOC, we get 180º. ∠AOC and ∠BOC are Supplementary Angles.
∠AOC + ∠BOC = 180°

Properties of Supplementary Angles

Have a look at the important properties of supplementary angles explained in the below modules. They are as such

• The two angles are said to be supplementary angles when they add up to form 180°.
• The two supplementary angles together make a straight line, but the angles need not be together.
• Two acute angles cannot be a supplement by each other.
• “S” of supplementary angles stands for the “Straight” line. This means they form 180°.
• The two right angles are always supplementary.

Adjacent and Non-Adjacent Supplementary Angles

The supplementary angles may be classified as either adjacent or non-adjacent. The adjacent supplementary angles have the common line segment or arm with each other. Also, the non-adjacent supplementary angles do not have the line segment or arm.

Supplementary Angles Theorem

The supplementary angle theorem states that if two angles are supplementary to the same angle, then the two angles are said to be congruent.

Proof:

If ∠a and ∠b are two different angles that are supplementary to a third angle ∠c, such that,
∠a + ∠c = 180 ……. (1)
∠b + ∠c = 180 ……. (2)
Then, from the above two equations, we can say,
∠a = ∠b

Hence proved.

Supplementary Angles Examples

1. Verify if 125°, 55° are a pair of supplementary angles?

Solution:
Add the given two angles and check if the resultant angle is 180° or not.
125° + 55° = 180°

The resultant angle is 180°. Hence, they are a pair of supplementary angles.

2. Find the supplement of the angle (30 + x)°.

Solution:
To find the supplement of (30 + x)°, subtract it from 180°
Supplement of the angle (30 + x)° = 180° – (30 + x)°
= 180° – 30° – x°
= (150 – x) °

3. If angles of measures (y – 2)° and (3y + 7)° are a pair of supplementary angles. Find the measures.

Solution:
Since (y – 2)° and (3y + 7)° represent a pair of supplementary angles, then their sum must be equal to 180°.
Therefore, (y – 2) + (3y + 7) = 180
y – 2 + 3y + 7 = 180
y + 3y – 2 + 7 = 180
4y + 5 = 180
Subtract 5 from both sides
4y + 5 – 5 = 180 – 5
4y = 180 – 5
4y = 175
y = 175/4
y = 43.75°

Therefore, we know the value of y = 43.75°, put the value in place of y
y – 2
= 43.75 – 2
= 41.75°

And again, 3y + 7
= 3 × 43.75° + 7
= 118 + 5
= 138.25°
Therefore, the two supplementary angles are 41.75° and 138.25°.

4. Two supplementary angles are in the ratio 5 : 4. Find the measure of the angles.

Solution:
Let the common ratio be m.
If one angle is 5m, then the other angle is 4m.
Therefore, 5m + 4m = 180
9m = 180
m = 180/9
m = 20
Put the value of m = 20

One angle is 5m
= 5 × 20
= 100°

And the other angle is 4m
= 4 × 20
= 80°

Therefore, the two supplementary angles are 100° and 80°.

5. In the given figure find the measure of the unknown angle.

Solution:
x + 45° + 25° = 180°
The sum of angles at a point on a line on one side of it is 180°
Therefore, x + 70° = 180°
Subtract 70° from both sides
x + 70° – 70° = 180° – 70°
x = 110°

Complementary Angles are the angles with 90°. When we add two angles then the resultant angle should be 90° to call those angles complementary angles. In complementary angles, each angle complements another angle. If an angle is 90 degrees, then it can’t be called a complementary because it doesn’t have any pairs. It consists of only one angle with 90 degrees.

The angles become complementary when the sum of the two angles becomes 90 degrees. Therefore, an angle with 90 degrees cannot be called complementary angles. Find all the Lines and Angles concepts on our website with solved examples.

From the above figure, the ∠AOB and ∠BOC are complementary as ∠AOB + ∠BOC = 35° + 55° = 90°. Therefore, they both are Complementary Angles. Also, angles 35 and angle 55 complements each other.

Example 1: If you take a triangle with one angle of 50 degrees and another angle of 40 degrees, the combined angle will become 90 degrees. The two 40 and 50 angles are called complementary angles.

Example 2: If you take a triangle with one angle of 15 degrees and another angle of 75 degrees, the combined angle will become 90 degrees. The two 15 and 75 angles are called complementary angles.

Example 3: If you take a triangle with one angle of 10 degrees and another angle of 80 degrees, the combined angle will become 90 degrees. The two 10 and 80 angles are called complementary angles.

Observations of Complementary Angles

• If two angles complement each other, then each angle must be an acute angle. But any two acute angles need not be complementary.
  For example, angles of measures 30° and 40° are not a complement to each other.
• Two right angles cannot complement each other.
• Also, two obtuse angles cannot complement each other.

Complementary Angles Examples

1. Find the complement of below angles

(a) 58°

Solution:
To find the complement of 58°, subtract it from 90°
90° – 58° = 32°

Therefore, the complement of 58° is 32°

(b) 37°40′

Solution:
To find the complement of 37°40′, subtract it from 90°
90° – 37°40′
90° = 89°60′
= 89°60′ – 37°40′
= 52°20′
Therefore, the complement of 37°40′ is 52°20′

(c) y + 42°

Solution:
To find the complement of y + 42°, subtract it from 90°
90° – (y + 42°)
= 90° – y – 42°
= 56° – y
Therefore, the complement of y + 42° is 56° – y

2. Find the complement of the angle (20 + x)°

Solution:
To find the complement of (20 + x)°, subtract it from 90°
90° – (20 + x)
= 90° – 20 – x°
= 70° – x° = (70 – x)°
Therefore, the complement of (20 + x)° is (70 – x)°

3. Find the measure of an angle that is 36° less than its complement.

Solution:
Let the unknown angle be y, then measure of its complement = (90° – y)
According to the given question,
(90° – y) – y = 36°
90° – y – y = 36°
90° – 2y = 36°
Subtract 90° from both sides
90° – 90° – 2y = 36° – 90°
-2y = -54°
y = 54/2 = 27°
y = 27°
Therefore, 90 – y (Put the value of y = 27°)
= 90 – 27°
= 63°
Therefore, the pair of complementary angles are 63° and 27°

Have a look at Some Geometric Terms and Results. We have given a useful reference of geometric terms and their definitions along with solved examples. Most of the students feel difficult to understand Some Geometric Terms. So, to help such students, we explained all Geometric Terms in a clear and understandable way. We can get strong and exact results using Certain Geometric Statements. So, make use of the given formulas and get the easy process to solve problems.

We have also given Lines and Angles concepts and problems for free of cost on our website.

Some Geometric Terms and Results

• The sum of all the angles at a point is 360°.

i.e., ∠7 + ∠8 + ∠9 + ∠10 + ∠11 + ∠12 = 360°

• The sum of all the angles about a point on a straight line on one side of if it is 180°.

i.e., ∠5 + ∠6 + ∠7 + ∠8 = 360°

Some Important Geometric Terms

1. Equal Angles

The two angles are considered to be equal if they have the same degree measure.

Given that two angles. The angles are ∠ABC and ∠PQR.
∠ABC = 90°; ∠PQR = 90°.
∠ABC and ∠PQR are equal angles of measure 90°.

2. Bisector of an Angle

A ray that divides the given angle into two equal angles is called an angle bisector.

Given that ∠XYZ along with a ray YO that divides ∠XYZ. In the adjoining figure, the ray YO divides ∠XYZ into two equal angles ∠XYO and ∠OYZ
i.e., ∠XYO = ∠OYZ.

3. Perpendicular Lines

Perpendicular Lines are the lines that intersect each other to form right tangles between them. In the adjoining e, lines AB and CD intersect at 0 such that ∠COB = ∠ COA = ∠AOD = ∠BOD = 90°.
Therefore, we say that AB is perpendicular to CD, i.e., (AB ⊥ CD).

4. Perpendicular Bisector

Perpendicular Bisector is the line that passes through the midpoint of the given line segment and also it is perpendicular to it. Here, the CD is the line segment. AB is the perpendicular bisector as ∠AOB = ∠AOD = 90° and CO = OD.