Common Core Math

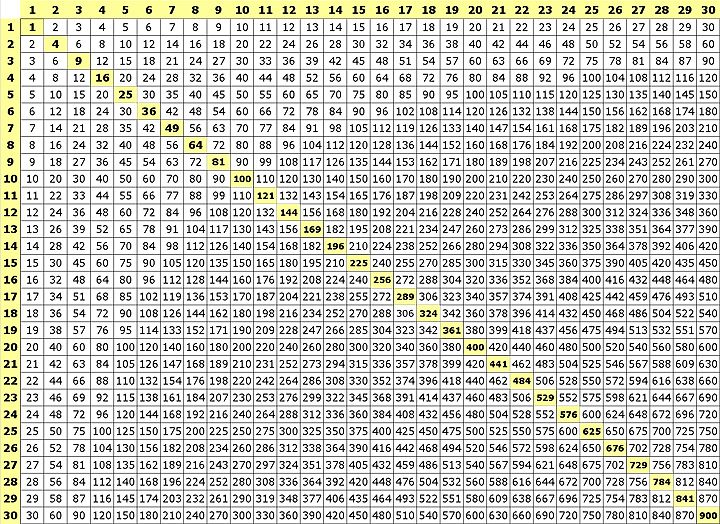
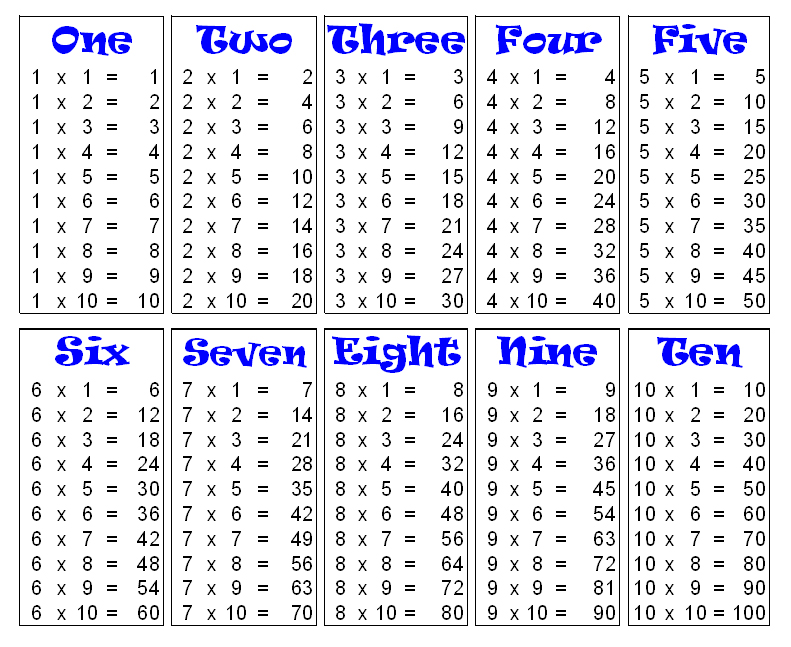
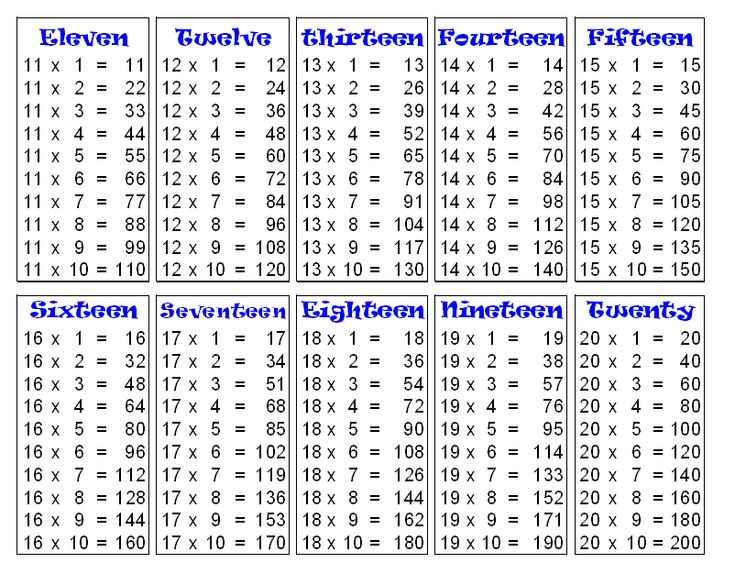
Find Multiplication Tables for 1 to 100 here on this web page. Enhance your math skills by learning the Math Tables from 1 to 30. Answer any kind of math problem easily taking the help of the Multiplication Tables available. Use the Tables of One to Hundred provided below in image and tabular format. You can download them and prepare offline too and score better grades in the exams.

Also, Read:

• Math Tables 1 to 30
• Math Tables 1 to 20

Tables from 1 to 100

Here is the list of 100 Tables provided in tabular format. Having strong fundamentals of these Tables will aid you to solve any kind of Mathematical Problem easily and efficiently. Learn the Math Multiplication Tables from One to Hundred by referring to the below sections.

Multiplication Tables of 1 to 10

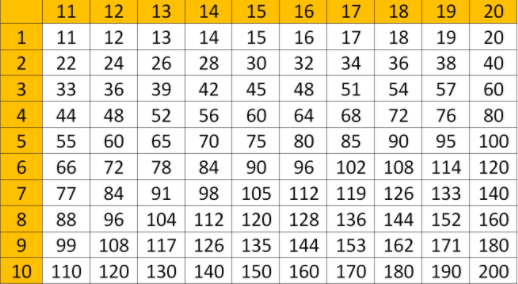
Multiplication Tables of 11 to 20

Multiplication Tables of 21 to 30

Multiplication Tables of 31 to 40

Multiplication Tables of 41 to 50

Multiplication Tables of 51 to 60

Multiplication Tables of 61 to 70

Multiplication Tables of 71 to 80

If you are in search of Multiplication Charts for 1 to 30 then you can halt your search as you have arrived at the right page. To make your math calculations quite easy we have presented the Math Times Tables in both image and Tabular Format for your reference. Learning the Math Tables from 1 to 30 students can solve their math problems effortlessly and do quick calculations.

Read More Tables:

• Math Tables 1 to 20
• Math Tables 1 to 12
• Math Tables 11 to 20

Multiplication Tables from 1 to 30

Learning Math Multiplication Tables helps students to develop mental math skills that can be of great help during their lives. Before you begin memorizing Math Multiplication Tables you need to visualize them and recite them until you recall a particular multiplication. Write the Math Tables from 1 to 30 repeatedly so that you can memorize them easily.

Tables of 1 to 10

Tables of 11 to 20

Tables of 21 to 30

Math Tables Chart for 1 to 30

You can remember the Math Times Tables from 1to 30 easily by the traditional rote learning method. You can do so by memorizing the numbers in the column table. The table below illustrates the multiplication tables from One to Thirty.

Tables from 1 to 30 in PDF’s

Here is the list of Multiplication Tables arranged for all the 30 Tables in PDF Form via quick links. Just tap on them and learn the entire multiplication chart of it efficiently. Use them for basic calculations involved in division and multiplication.

Tips to Learn Math Tables from 1 to 30

Go through the below-listed tips & tricks while learning the Multiplication Tables and they are in the following fashion. They are as follows

• While multiplying two numbers the order doesn’t matter and the result is always the same no matter we multiply the first number with a second number or a second number with the first number.
• It can be difficult to learn the entire Multiplication Chart at once so try to learn it in chunks.
• Try to understand the patterns so that it would be easy for you to memorize the Multiplication Tables.
• For Example, 2 Tables can be remembered easily by doubling the number. When it comes to the 5 Table the pattern is 5, 10, 15, 20, 25, 30…..
• For 10 Table simply place zero at the end of the given number. For Example 5 x 10 = 50, 8 x 10 =80,….

FAQs on Math Multiplication Tables from One to Thirty

1. How to Write the Multiplication Table of 9?

Table of 9 is written as follows:

9 x 1 = 9

9 x 2 = 18

9 x 3 = 27

9 x 4 = 36

9 x 5 =45

9 x 6 = 54

9 x 7 = 63

9 x 8 = 72

9 x 9 =81

9 x10 =90

2. How to Memorize the 10 Times Table?

You can remember the Table of 10 easily by simply appending it with zeros at the end of the given number. For example, 7 times 10 is equal to 70.

3. How many times should we multiply 9 to get 72?

Using the Tables from 1 to 30 we know 9 times 8 is 72, thus 9 has to be multiplied 8 times to get 72.

4. Using the tables from 1 to 30, find the value of 7 plus 20 times 3 minus 20 times 5?

From Table of 20, we know 20 times 3 is 60 and 20 times 5 is 100

Writing it in statement form we get 7+20 times 3+20 times 5

= 7+60+100

= 167

Find a way for converting Roman Numerals to Numbers. You can learn about the basic details such as Roman Number Definition, Procedure for Converting Roman Numerals to Numbers. You can also check the solved Examples on how to change Roman Numerals to Numbers by going through this article completely.

Do Check:

• Conversion of Numbers to Roman Numerals
• Rules For Formation of Roman Numerals
• Roman Numerals

Roman Numerals – Definition

Romans used some roman alphabets to specify numbers. These are called Roman Numerals. Roman Numerals are nothing but English alphabets except j, u, and w. There are seven Roman numerals. Roman Numerals are I, V, X, C, L, D, and M. Bar on the Roman letters means its value is multiplied by 1000 times. The values of Roman Numerals are as follows

Roman Numeral Chart for 1 to 1000 Numbers

How to Convert Roman Numerals to Numerals?

For a given roman numeral r

• Find the largest roman numeral(n) with the large decimal value(v) taken from the  roman numeral r:

• If the largest numeral appears first then count how many times it appears. It appears a Maximum of three times. Multiply its value by the number of times it appeared. The value V of the roman number is added to the decimal number x.
• If the largest numeral appears second then subtract the value of the numeral before it from its value. The value v of the Roman Numeral is added to the decimal number X.

X=X + V

• Repeat steps 1 to 3 until you find Roman Numerals of r.

Roman Numerals to Numbers Conversion Examples

1. Convert the roman numeral XXXVII to Number?

Solution:

In this example, Highest Roman Numeral is X. Roman Numeral X appeared three times. The value of X multiplied by three times. So the decimal number (X) has 30. The Second highest decimal number is V and its value is 5 and it is added to the decimal number. I is appearing two times and its value is 1 and it is added to a decimal number(X). Therefore, the given roman number XXXVII converted to numbers is 37.

2. Convert Roman Numeral MMXXI to Number?

Solution:

In this example, Highest Roman Numeral is M. Roman Numeral M appeared two times. The value of M multiplied by two times.so the decimal number X has 2000. Second, the highest decimal number is X and its value is 10 and it appeared two times. Its value is added to the decimal number. Now decimal number(X) has 2020. I appear one-time. Its value is 1 and it is added to the decimal number. Thus given number MMXXI converted to Numbers is 2021.

3. Convert Roman Numeral CDLII to Number?

Solution:

In this example, Highest Roman Numeral is D. It appeared second of the Roman Numeral, so subtract the value of the Roman Numeral before its value.  so the decimal number( X) has 400. Roman Numeral L has the decimal value 50 and it is added to a decimal number(X). The value of I is 1 and it is added to a decimal number. The given number is 451.

4. Convert Roman Numeral CCCL to Number?

Solution:

In this example, Highest Roman Numeral is c. Roman Numeral C appeared three times. The value of X multiplied by three times. So the decimal number X has 300.second highest decimal number is L. Its value is 50 and it is added to a decimal number(X). The given number CCCL is 350.

FAQ’s on Conversion of Roman Numerals to Numbers

1. What is the value of XLVI?

Here the largest value of the Roman Numeral is L. since it is placed second the value of the L numeral is subtracted from first. So the total is 40. The values of V and I are added to the total. The value of XLVI is 46.

2. What is the value of L in Roman Numerals?

The value of L in Roman Numerals is 50.

3. Why bar is placed on the Roman Numeral?

when a bar is placed on the roman numeral its value is increased by 1000 times.

4. What is the value of M?

The value of M is 1000.

Tally marks are most ordinarily used to represent the scoreboard in games and sports. The frequency of knowledge is often represented using Tally Marks. Tally Marks are also called Hash Marks. It is denoted by a single vertical bar ‘ | ‘. You may use the tally for solving addition, subtraction, or word problems. Before numbers were invented people found it difficult to stay records of their belongings and then they used to count by sticks which are further referred to as Tally Marks.

Read More: Frequency Distribution of Ungrouped and Grouped Data

Tally Marks – Definition

Tally marks are defined as a way to record or mark your counting. It is a numeral system used to make counting easier. The general way of tally marks writing may be a group or set of 5 lines, in these five lines first four lines are drawn vertically and each fifth line runs diagonally over the four vertical lines it means from the top of the first line to the bottom of the fourth line.

Tally marks are commonly used for counting the points, scores, many people like that, these tally marks will differ from country to country because each country has developed with their own system. The tally marks are expressed as shown below

Counting Tally Marks

Let us see how to use tally marks for counting numbers 1 to 10. Tally marks are the quickest way of keeping track of numbers during a group of five.

How to represent the numbers in Tally Marks?

• One is represented by ‘I’
• Two is represented by ‘II’
• Three is represented by ‘III’
• Four is represented by ‘IIII’
• Five is not represented by ‘IIIII’, it is represented as four vertical lines and one cross line (diagonal line) it means from the top of the first line to the bottom of the fourth line.
• Six is represented by a set of five lines with ‘I’
• Seven is represented by the set of five lines with ‘II’
• Eight is represented by the set of five lines with ‘III’
• Nine is represented by the set of five lines with ‘IIII’
• Ten is represented by 2 (two) sets of five lines.

Tally Mark Chart

Tally charts are used to collect the data efficiently and quickly. A Tally Mark chart or a Tally Mark graph is a graphical representation of data in statistics, so it is beneficial in scanning the data. A tally chart filling with marks is represented by numbers is quicker than writing out figures or words, then the information is collected into sub-groups, making it easy to research.

In a tally mark graph has first four numbers lines are represented by vertical lines and the fifth line is represented by a diagonal (/) line across the four vertical lines. The tally marks chart contains the number from 1 to 10 is as shown below,

Tally Marks are used for finding the frequency of the set of data values specifically for the raw data or ungrouped data. consider an example, asked to create the frequency distribution provided with raw data or random values. In this case, we may have to make either for class intervals or individual observations.

Now, we count all occurrences of a single data value or a class interval in one go, then we have to cross-check the entire list again and again for the next class interval or individual observation. Therefore this will be taking a lot of time for finishing. So, we can be reducing the complexity by making use of tally marks. The entire process can be done just by adding tally marks for each class interval or different observations.

Thus, we’ve to traverse the whole list of given data set on one occasion and then write the frequency numbers by counting the tally marks after completing the identification. So the obtained table is defined as the frequency distribution of the given data. The below example on tally marks will help you to understand the concept in a better way.

Tally Marks Examples

Example 1:

Below given the marks of 35 students on the Maths test (out of 10). Arrange those marks in tabular form using tally marks?

6, 1, 7, 8, 10, 9, 4, 2, 3, 7, 1, 8, 7, 5, 1, 4, 7, 6, 5, 2, 3, 8, 2, 4, 6, 2, 9, 3, 1, 4, 5, 7, 5, 10. Find the  

1. How many students scored more than 8 marks?
2. How many students scored less than & equal to 5?
3. What are the marks scored by the maximum students? what is the number of students?

Solution:

Given the marks of 35 students in Maths test. The frequency table of given data is as shown below

(i) Given the 35 students’ marks out of 10 in the maths test.

Now, we can find the number of students with more than 8,

The number of students with more than 8 marks is, 3 + 2 = 5

Therefore the total number of students with more than 8 marks is 5.

(ii) Given the 35 students’ marks out of 10 in the maths test.

Now, we can find the number of students who scored less than and equal to 5.

The number of students who scored less than and equal to 5 is,

= 4 + 4+ 3+ 4 + 4

= 19

Therefore, the number of students who scored less than and equal to 5 is 19.

(iii) Given the 35 students’ marks out of 10 in the maths test.

Now, we can find the maximum number of students who scored 5 marks.

The maximum number of students who scored 5 marks is 5.

The maximum number of students scored 5 marks. The number of students is 5.

FAQ’S on Tally Marks

1. What is Tally Mark Chart?

Tally Mark charts are used to collect the data efficiently and quickly. A Tally Mark chart is a graphical representation of data in statistics, so it is beneficial in scanning the data. A tally chart filling with marks is represented by numbers is faster than writing out figures or words, then the data is collected into sub-groups, making it easy to analyze.

2. Define Tally Frequency Table?

The Tally Frequency table is defined as a method of collecting the data with the tally marks, tally frequency table is also known as Tally Chart.

3. Why should Tally marks be essential?

Tally marks are very important mainly use to keep the record of a running or continuous count. These tally marks are so useful for maintaining and recording the scores in a game or a sport.

5. What are the advantages of Tally Marks?

The advantages of tally marks are

1. Enables Effortlessness in data movements
2. Fewer expenses on data collection and data transfer of files.
3. Helps for easy and fast documents access.

A set of a pack of well-defined objects. Those objects are called the elements or members of a set. The complement of a set is nothing but the subtraction of a universal set from any of the given set. The set complement contains the non-common elements of the universal set. Get to know more about the complement of a set, its definition, and the process to calculate the set complement from this page. You can also see the solved examples for a better understanding of the concept.

Complement of a Set – Definition

Complement of a set A is denoted by A^c or A’.  The complement of set A means Universal set minus set A. The complement set gets the set of elements in the universal set that are not in set A.

The set builder form of set complement is A’ = {x: x ∈ U and x ∉ A}

The Venn diagram of the complement of a set A is

The important points about the set complement are provided here.

• The set and its complement are disjoint sets
• The complement of an empty set is a universal set.
• The complement of a universal set is an empty set.

How to find the Complement of a Set?

Grab the detailed step-by-step explanation on how to calculate the complement of a set from the following sections.

• At first, you need to take two sets universal set and anyone set.
• Set complement = Universal_Set – Given_Set
• In the resultant complement set, you need to write the elements of a universal set that are not elements of the given set.

Properties of Complement Sets

(i) Complement Law

A U A’ = A ‘ U A

(A ∩ B’) = ϕ

(ii) Law of Complementation

(A’)’ = A

(iii) De Morgan’s Law

(A ∩ B’) = ϕ

(A U B) = A’ ∩ B’

(iv) Law of Empty Set

ϕ’ = ∪

(v) Law of Universal Set

∪’ = ϕ

Have a look at the solved example problems on the set complement to get a better idea of the concept easily.

Also, Read

Complement of a Set Examples

Example 1:

If A = {1, 3, 5, 7, 9, 11}, ∪ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, find the complement of A.

Solution:

Given sets are

A = {1, 3, 5, 7, 9, 11}, ∪ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

A^c = ∪ – A

= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} – {1, 3, 5, 7, 9, 11}

= {2, 4, 6, 8, 10}

Therefore, A^c = {2, 4, 6, 8, 10}

Example 2:

If ∪ = {5, 10, 15, 20, 25, 30, 35}, B = {10, 20, 30, 40, 50, 60}, evaluate the complement of set B.

Solution:

Given sets are

∪ = {5, 10, 15, 20, 25, 30, 35}, B = {10, 20, 30, 40, 50, 60}

B’ = ∪ – B

B’ means include the elements of the universal set that are not in set B.

B’ = {5, 10, 15, 20, 25, 30, 35} – {10, 20, 30, 40, 50, 60}

= {5, 15, 25, 35}

Therefore, B’ = {5, 15, 25, 35}.

Example 3:

If P = {2, 3, 5, 7, 9}, Q = {1, 4, 5, 8, 10}, ∪ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, then prove that (P ∩ Q)’ = P’ ∪ Q’

Solution:

Given sets are

P = {2, 3, 5, 7, 9}, Q = {1, 4, 5, 8, 10}, ∪ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

P’ = ∪ – P

= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} – {2, 3, 5, 7, 9}

= {1, 4, 6, 8, 10}

Q’ = ∪ – Q

= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} – {1, 4, 5, 8, 10}

= {2, 3, 6, 7, 9}

P ∩ Q = {2, 3, 5, 7, 9} ∩ {1, 4, 5, 8, 10}

= {5}

L.H.S = (P ∩ Q)’

= ∪ – (P ∩ Q)

= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} – {5}

= {1, 2, 3, 4, 6, 7, 8, 9, 10}

R.H.S = P’ ∪ Q’

= {1, 4, 6, 8, 10} ∪ {2, 3, 6, 7, 9}

= {1, 2, 3, 4, 6, 8, 7, 9, 10}

L.H.S = R.H.S

Hence, proved.

Example 4:

If A = {l, a, d, r}, ∪ = {a, b, c, d, k, l, r, s t, y},  then show that A ∪ A’ = A’ ∪ A = ∪

Solution:

Given sets are

A = {l, a, d, r}, ∪ = {a, b, c, d, k, l, r, s t, y}

To prove that, A ∪ A’ = A’ ∪ A = ∪

A’ = ∪ – A

= {a, b, c, d, k, l, r, s t, y} – {l, a, d, r}

= {b, c, k, s, t, y}

A ∪ A’ = {l, a, d, r} ∪ {b, c, k, s, t, y}

= {l, a, d, r, b, c, k, s, t, y} = ∪

A’ ∪ A = {b, c, k, s, t, y} ∪ {l, a, d, r}

= {b, c, k, s, t, y, l, a, d, r} = ∪

Hence, shown.

FAQs on Set Complement

1. Which law deals with the complement of a set?

The various laws which deal with the set complement are listed here.

Complement laws (union and intersection) A ∪ A’ = U, A ∩ A’ = ∅

Law of double complementation (A’)’ = A

Law of empty and universal set ∅’ = U, U’ = ∅

De Morgan’s Complement Law (A∪B)’ = A’ ∩ B’, (A ∩ B)’ = A’ ∪ B’

2. How do you solve complements of a set?

The complement of a set is obtained by subtracting the universal set from the given set. The resultant set complement has the set of elements that are in the universal set and not in the given set.

3. What is the symbol of a complement of a set?

The complement of a set M is represented as M’ or M^c.

4. What is a universal set?

A universal set is a set that includes all the elements of other sets, including its own elements. It is represented by ‘U’.

Sets are the collection of well-defined elements. When you try to combine two sets under some conditions to form a new set, it is called a difference of two sets. Moreover, the set difference is one of the operations on sets. By using the set difference, you can just perform operations between only two sets. Check out what is set difference, how to find the difference between two sets, and solved examples in the following sections.

What is meant by Set Difference?

The difference between two sets A and B is represented as A – B. The set difference of A and B is another set that includes the elements A and but not the elements of B. “A – B” can be read as set A minus set B. A – B can also be written as A / B.

Therefore, A – B = {x : x ∈ A and x ∉ B}

The two important properties of the difference of two sets are

• A – B ≠ B – A
• If A, B are two disjoint sets, then A – B = A and B – A = B.

Also, Read

How to find the Difference of Two Sets?

Follow these simple steps to calculate the difference between the two sets.

• Let us take two sets having well-defined objects of the same type.
• The two sets names can be P and Q.
• In P – Q, you must include the elements of P but not elements of Q.
• Q – P means include elements of Q but not elements of P.

Difference of Two Sets Example Questions and Answers

Example 1:

If A = {25, 5, 50, 23}, B = {1, 5, 10, 20, 25, 50}, then find A – B and B – A.

Solution:

The given two sets are A = {25, 5, 50, 23}, B = {1, 5, 10, 20, 25, 50}

A – B = {25, 5, 50, 23} – {1, 5, 10, 20, 25, 50}

= {23}

B – A = {1, 5, 10, 20, 25, 50} – {25, 5, 50, 23}

= {1, 10, 20}

Therefore, A – B = {23} and B – A = {1, 10, 20}.

Example 2:

If P = {m, n, o, p, q, x, y, z}, Q = {o, p, q, y}

find P – Q and Q – P.

Solution:

The given two sets are P = {m, n, o, p, q, x, y, z}, Q = {w, r, s, t, o, p, q, y}

P – Q means elements of P but not the elements of Q.

P – Q = {m, n, o, p, q, x, y, z} – {w, r, s, t, o, p, q, y}

= {m, n, x, z}

Q – P means the elements of Q but not the elements of P.

Q – P = {w, r, s, t, o, p, q, y} – {m, n, o, p, q, x, y, z}

= {w, r, s, t}

Therefore, P – Q = {m, n, x, z}, Q – P = {w, r, s, t}.

Example 3:

If A = {x : x is a natural number between 10 and 20}, B = {x : x is a even number between 10 and 25} and C = {3, 6, 7, 14, 4, 8}

find B – C, A – B, C – A, A – C, and C – B

Solution:

The given three sets are A = {x : x is a natural number between 10 and 20}, B = {x : x is a even number between 10 and 25} and C = {3, 6, 7, 14, 4, 8}

The roster form of A = {10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}

The roster form of B = {10, 12, 14, 16, 18, 20, 22, 24}

B – C = {10, 12, 14, 16, 18, 20, 22, 24} – {3, 6, 7, 14, 4, 8}

= {10, 12, 16, 18, 20, 22, 24}

A – B = {10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20} – {10, 12, 14, 16, 18, 20, 22, 24}

= {11, 13, 15, 17, 19}

C – A = {3, 6, 7, 14, 4, 8} – {10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}

= {3, 6, 7, 4 8}

A – C = {10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20} – {3, 6, 7, 14, 4, 8}

= {10, 11, 12, 13, 15, 16, 17, 18, 19, 20}

C – B = {3, 6, 7, 14, 4, 8} – {10, 12, 14, 16, 18, 20, 22, 24}

= {3, 6, 7, 4, 8}

Example 4:

If X = {21, 23, 25}, Y = {32, 34, 36} find X – Y and Y – X

Solution:

The given two sets are X = {21, 23, 25}, Y = {32, 34, 36}

X – Y = {21, 23, 25} – {32, 34, 36}

= {21, 23, 25}

Y – X = {32, 34, 36} – {21, 23, 25}

= {32, 34, 36}

Therefore, X – Y = X and Y – X = Y.

FAQs on Difference of Two Sets

1. What is the difference of set?

The difference between the two sets is denoted as the first set – the second set. While you are evaluating the difference, just include the non common elements of the first set in the result set.

2. How do you subtract two sets?

The subtraction (difference) of two non-empty sets A and B is A – B. A – B = {x : x ∈ A and x ∉ B}. The difference between the two sets means includes the elements of A but not elements of B.

3. How do you solve the complement of sets?

The complement of a set means subtract U and that set. Complement of set B = U – B. Here U is the universal set. The complement of B means the elements of U but not the elements of B.

4. Why A – B is not equal to B – A?

A – B means the elements of A by eliminating the common elements between A and B. B – A means the elements of B by removing the common elements between A and B. So, A – B is not equal to B – A.

Sets are a collection of well-defined objects. If two are more sets are combined to form one set under the special conditions, then set operations are carried out. Students who want to know more about the Operations on Sets can check the below sections. On this page, we will provide detailed information like set operations definitions, examples, and Venn diagrams to understand them clearly.

What are Set Operations?

Sets operations come into existence when two or more sets are joined to form one set under some conditions. Basically, we have 4 types of operations on sets. They are

• Union of Sets
• Intersection of Sets
• Complement of the Sets
• Cartesian Product of Sets

Operations on Sets

Here we will discuss each of the sets operations in detail along with the examples.

1. Union of Sets

The union of two sets A and B is a set of elements that are in both A and. It is denoted by A U B.

So, A U B = { x | x ∈ A or x ∈ B }.

Examples:

If A = {1, 4, 8, 16, 32}, B = {3, 9, 27, 1, 6}

Now write every element of A and B in A U B without repetition.

A U B = {1, 3, 4, 6, 8, 9, 16, 27, 32}

2. Intersection of Sets

The intersection of two sets A and B means the set of elements that are common in both A and B. It is denoted by A ∩ B.

Therefore, A ∩ B = { x : x ∈ A and x ∈ B }.

Examples:

If A = {1, 4, 5, 10, 15, 8, 9}, B = {5, 10, 20, 25, 30}

Now we write the common elements from both sets A and B.

A ∩ B = {5, 10}

3. Difference or Complement of Set

when A and B are two sets, then their difference A – B means the elements of A but not the elements of B.

A minus B can be written as A – B.

A – B = {x : x ∈ A, and x ∉ B}

A – B never equal to B – A. i.e A – B ≠ B – A

If A and B are disjoint sets, then A – B = A and B – A = B.

Examples:

If A = {2, 4, 3, 6, 4, 8, 5, 10} and B = {1, 2, 3, 4}

Then, A – B includes elements of A but not elements of B.

A – B = {5, 6, 8, 10}

Complement of a Set

The complement of a set is the set of elements that are not in that set. The complement of set a is denoted by A’.

Therefore, A’ = {x | x ∉ A }

A’ = (U – A) here U is the universal set that contains all elements.

Examples:

A = { x : x belongs to set of even integers }

U = {x : x belongs to set of integers}

A’ = U – A

So, A’ = {x : x belongs to set of odd integers}

4. Cartesian Product or Cross Product

The cartesian product of two non-empty sets A and B are denoted by A x B. The cross product is the set of all ordered pair of elements from A and B. The cartesian product is also known as the cross product.

A x B = { (a, b) | a ∈ A and b ∈ B }

The cross product of two sets A x B and B x A do not contain exactly the same ordered pairs.

So, A x B ≠ B x A.

Examples:

If A = {4, 5, 6} and B = (a, b}

The cross product of A and B have 6 ordered pairs.

A x B = {(4, a), (4, b), (5, a), (5, b), (6, a), (6, b)}

B x A = {(a, 4), (a, 5), (a, 6), (b, 4), (b, 5), (b, 6)}

Properties of Cartesian Product

• It is non-commutative. i.e A x B ≠ B x A
• A x B = B x A, when A = B
• A x B = { }, if either A = ∅ or B = ∅
• The cartesian product is non-associative. i.e (A x B) x C ≠ A x (B x C)
• Distributive property over intersection, union and set difference are
  • A x (B U C) = (Ax B) U (A x C)
  • A x (B ∩ C) = (A x B) ∩ (A x C)
  • A x (B/C) = (A x B) / (Ax C)

Set Operations and Examples

Question 1:

If A = {1, 3, 5, 7}, B = {2, 4, 6, 8}, C = {1, 2, 3, 4}, D = {5, 6, 7, 8}, U = {1, 2, 3, 4, 5, 6, 7, 8} find

(i) A U B

(ii) A ∩ C

(iii) D’

Solution:

Given sets are

A = {1, 3, 5, 7}, B = {2, 4, 6, 8}, C = {1, 2, 3, 4}, D = {5, 6, 7, 8}, U = {1, 2, 3, 4, 5, 6, 7, 8}

(i) A U B = {1, 3, 5, 7} U {2, 4, 6, 8}

= {1, 2, 3, 4, 5, 6, 7, 8}

So, A U B = {1, 2, 3, 4, 5, 6, 7, 8}

(ii) A ∩ C = {1, 3, 5, 7} ∩ {1, 2, 3, 4}

= {1, 3}

So, A ∩ C = {1, 3}

(iii) D’ = U – D

= {1, 2, 3, 4, 5, 6, 7, 8} – {5, 6, 7, 8}

= {1, 2, 3, 4}

So, D’ = {1, 2, 3, 4}

Question 2:

If A = {10, 12, 15, 18}, B = {11, 15, 14, 16}, C = {15, 16, 18, 7} find

(i) A – B

(ii) B – A

(iii) A – C

Solution:

Given sets are

A = {10, 12, 15, 18}, B = {11, 15, 14, 16}, C = {15, 16, 18, 7}

(i) A – B = {10, 12, 15, 18} – {11, 15, 14, 16}

= {10, 12, 18}

So, A – B = {10, 12, 18}

(ii) B – A = {11, 15, 14, 16} – {10, 12, 15, 18}

= {11, 14, 16}

So, B – A = {11, 14, 16}

(iii) A – C = {10, 12, 15, 18} – {15, 16, 18, 7}

= {10, 12}

So, A – C = {10, 12}

Question 3:

If P = {a, b, d}, Q = {m, n, o}, R = {l, e, t, t, e, r} find

(i) P x Q

(ii) P x R

(iii) Q x R

Solution:

Given sets are

P = {a, b, d}, Q = {m, n, o}, R = {l, e, t, t, e, r}

(i) P x Q = {a, b, d} x {m, n, o}

= {(a, m), (a, n), (a, o), (b, m), (b, n), (b, o), (c, m), (c, n), (c, o)}

So, P x Q = {(a, m), (a, n), (a, o), (b, m), (b, n), (b, o), (c, m), (c, n), (c, o)}

(ii) P x R = {a, b, d} x {l, e, t, t, e, r}

= { (a, l), (a, e), (a, t), (a, r), (b, l), (b, e), (b, t), (b, r), (d, l), (d, e), (d, t), (d, r) }

So, P x R = { (a, l), (a, e), (a, t), (a, r), (b, l), (b, e), (b, t), (b, r), (d, l), (d, e), (d, t), (d, r) }

(iii) Q x R = {m, n, o} x {l, e, t, t, e, r}

= {(m l), (m, e), (m, t), (m, r), (n, l), (n, e), (n, t), (n, r), (o, l), (o, e), (o, t), (o, r)}

So, Q x R = {(m l), (m, e), (m, t), (m, r), (n, l), (n, e), (n, t), (n, r), (o, l), (o, e), (o, t), (o, r)}

Read More Related Articles:

FAQs on Sets Operations

1. What are the 4 operations of sets?

The four basic operations on sets are the union of sets, the intersection of sets, set difference, and the cartesian product of sets. When two sets are combined under some constraints, then we use these set operations.

2. How can operations be performed on sets?

Based on the constraints when joining two sets, operations on sets are performed. Union means adding the elements of both sets, intersection means adding common elements from two sets, difference means adding the elements of the first set but not the second set. Cross product gives the ordered pairs, by taking the elements from both sets.

3. How to find A x B in sets?

A x B means the cross product of two sets A and B which means the set of ordered pairs (a, b) where a ∈ A, b ∈ B. The set builder form is A x B = { (a,b) |a ∈ A,b ∈ B }.

4. What are the properties of set operations?

The properties of set operations are commutative property, distributive property, associative property, identity property, idempotent, and complement.

Searching for help regarding the concept of Class Limits in Statistics? If so, you have come the right way and you will get a complete idea of the entire concept by going through this article. Check class limits definition, types, the procedure to find the class limits from data in the forthcoming modules. Get to know about the lower and upper-class limits along with the steps to solve the class limits problems. Refer to the step-by-step procedure for solving questions related to class limits. Refer to all the definitions involved in it.

Do Read:

• Class Boundaries
• Frequency Distribution of Ungrouped and Grouped Data

Class Limits – Definition

To find the class limits there are numerous ways and methods to find the exact solution. There are two concepts involved in class limits. They are namely

1. Lower Class Limit

2. Upper-Class Limit

The class limits and the data values have the same accuracy rate and also have the same data values as the same number of decimal places. In this concept, the first-class interval extreme upper value and next class interval lower extreme value will not be equal. Class limits are considered as the maximum and minimum value of the class interval. Lower Class Limit is the minimum value of the interval and Upper-Class Limit is the maximum value of the interval.

How to find Class Limits?

While dealing with Class Limits in Statistics you will have two scenarios one is for overlapping groups and nonoverlapping groups. Refer to the following sections to get a complete idea of it.

1. Let the class intervals for some grouped data 10 – 15, 15 – 20, 20 – 25, 25 – 30, etc. In this case, the class intervals are overlapping and the distribution is continuous. 10, 15 are called the limits for the interval 10-15. However, 10 is the lower limit and 15 is the upper limit of the class.

In the same way, 15 and 20 are the lower and upper-class limits for the respective class interval 15-20. It is clear that the upper-class interval is the same as the lower limit for the next class interval in the case of overlapping groups.

2. Now, let us consider class intervals of grouped data to be 1-4, 5-8, 9 – 12, etc. in this the class intervals are non-overlapping and the distribution is discontinuous. 1, 4 are known as the class limits for the class interval 1-4 in which 1 is the lower class limit and 4 is the upper-class limit.

Similarly, 5 is the lower limit and 9 is the upper limit for the next interval 5-9. In this we can clearly observe that the upper limit of the class interval is not the same as a lower limit in the next class interval for nonoverlapping groups.

Class Mark or Mid Value or Midpoint

With respect to the class interval, it is defined as the average of two class boundaries or class limits. In other words, we can define it as the total or arithmetic mean of both class boundaries and class limits. Therefore, we have

Midpoint = LCL + UCL/2

= LCL + UCB/2

Class Boundaries

The class interval’s actual class limit is called the class boundary. For the classification of overlapping or classification of mutually exclusive which excludes some of the upper-class limits like 30-40,20-30,10-20 etc i.e., where the class limits and class boundaries coincide. Class boundaries are generally done for continuous variables. These are applicable for discrete variables that were mutually inclusive and non-overlapping classification which has the class limits like 20-29, 10-19, 0-9, etc.

LCB = LCL – (D/2)

UCB = UCL + (D/2)

where D is defined as the difference between the lower class limit of the next class interval and the upper-class limit of the given class interval.

Frequency Distribution

The frequency distribution divides the data and shows the number of data values that are present in each class.

Class Width

To find the class width, greatest data value – lowest data value /desired number of classes. If the value is in the decimal value, then round that value to the nearest convenient number.

Data Range for each class

LCL (Lower Class Limit) is the lowest data value that fits in the class

UCL (Upper-Class Limit) is the upper data that fits in the class

Frequency in the class

The number of values that fall in class is the frequency of the particular class.

Class Limits Example Problems with Solutions

Problem 1:

Data: 110, 122, 133 etc

Problem 2:

Data: 20.6, 11.7, 12.8 etc

Multiplication Tables from 11 to 20 help you learn the patterns and multiplication facts effortlessly. Math Tables for 11 to 20 can be quite essential for solving math problems on a quick basis. Tables of 11 to 20 are quite important for enhancing your math skills and arithmetic skills together. We have compiled the Multiplication Times Table from Eleven to Twenty both in the image and tabular format for free of cost.

Also, Check:

• Math Tables 1 to 20
• Math Tables 1 to 12

Tables from 11 to 20

For the sake of your comfort, we have attached the Multiplication Tables from 11 to 20 in Tabular Format. Use them as quick references and solve the math problems much efficiently and quickly. Learning the Multiplication Tables from Eleven to Twenty boosts your confidence and builds problem-solving skills in you. Make the most out of them and learn the solve the problems involving multiplication, division much simply.

Table of 11 to 15

Table of 16 to 20

Multiplication Table for 11 to 20

Below is the multiplication times table chart for tables 11 to 20. Use it as a reference to learn from 11 Times Table to 20 Times Table easily. It is as such

Tables 11 to 20 in PDF’s

Please find the below-attached Tables for 11 to 20 through the quick links provided below. Simply tap on the links and learn the entire table in no time.

FAQs on Tables from Eleven to Twenty

1. How to Memorize Tables from 11 to 20 Easily?

You can memorize the Tables from 11 to 20 easily by following the below-listed guidelines

• Write down the Math Tables on a piece of paper.
• Learn them orally and speak out in a loud voice.
• Solve Problems on Multiplication as much as possible.

2. What is the Table of 13?

Table of 13 is written as follows: 13 x 1 = 13, 13 x 2 = 26, 13 x 3 =39, 13 x 4 =52, 13 x 5 =65, 13 x 6= 78, 13 x7 =91, 13 x 8 =104, 13 x9 = 117, 13 x10 = 130.

3. How to learn Multiplication Table of 15 orally?

You can learn the Multiplication Table of 15 by reading as such

Fifteen ones are 15, Fifteen twos are 30, Fifteen threes are 45, Fifteen four’s are 60, Fifteen fives are 75, Fifteen sixes are 90, Fifteen seven’s are 105, Fifteen eights are 120, Fifteen nines are 135 and Fifteen ten’s are 150.

Students are advised to go through the Multiplication Tables from 1 to 12 for faster math calculations. These Math Tables are the basic ones and help you to do mental math calculations efficiently and quickly. We have provided Multiplication Tables for 1 to 12 both in image and PDF Format. We don’t charge any amount and you can download them for free and start practicing them. Learning these Multiplication Times Tables helps you to increase your speed of solving problems.

Do Check: Math Tables 1 to 20

Multiplication Table Chart for One to Twelve

Maths Times Tables 1 to 12 help you to learn and practice the multiplication facts easily. Multiplication Tables for 1 to 12 can be of extreme help in performing your math calculations. For your convenience, we have added the Math Tables for 1 to 12 in image format which you can download for free of cost and prepare every now and then. Students who learn these Math Tables can solve complex problems too easily.

Math Tables from 1 to 12

Here is the list of Tables from 1 to 12 in tabular format. Primary School Students are advised to go through these Multiplication Charts for One to Twelve to solve mathematical problems involving multiplication and division much easily. These Math Tables are the foundation blocks for many arithmetic calculations.

Table of 1 to 6

Table of 7 to 12

Multiplication Tables Chart for 1 to 12

Below is the Multiplication Table Chart for One to Twelve Tables and they are as such

Printable PDF’s of 1 to 12 Tables

FAQs on Tables from 1 to 12

1. How to Write the Table of 12?

Table of 12 is written as follows

12 x 1 =12

12 x 2 = 24

12 x 3 = 36

12 x 4 = 48

12 x 5 = 60

12 x 7 = 84

12 x 8 = 96

12 x 9 = 108

12 x 10 = 120

2. How to read 5 Times Table?

One time five is 5, two times five is 10, three times five is 15, four times five is 20, five times five is 25, six times five is 30, seven times five is 35, eight times five is 40, nine times five is 45 and ten times five is 50.

3. What is the 11 times table trick?

The trick for multiplying a single digit by 11 is to repeat the digit. For instance, to multiply 9 by 11 repeat the digit of 9 i.e. you will get 99.

Memorizing Multiplication Tables from 1 to 20 help you to related math calculations involving division, multiplication, fractions, algebra, taught in elementary school much simply. Without properly learning Math Tables you will feel difficulty in solving the math problems. Boost up your problem-solving skills and logical ability by memorizing the simple Math Multiplication Tables of 1 to 20 available here. Check out the Tips & Tricks to Memorize the Maths Times Tables provided in the later modules.

Multiplication Tables for One to Twenty

Boost up your math skills altogether by learning the Tables of 1 to 20 provided here. You can avail the Multiplication Tables from One to Twenty provided below in image format and download them free of cost. Stick it on your walls and recite it before going to bed and memorize it regularly.

Math Tables 1 to 20

Memorizing the Multiplication Tables one can boost their self-confidence and keep the information at one’s fingertips. Build memory in you and also enhances your problem-solving abilities. On Mastering the Multiplication Tables from 1 to 20 your speed of solving the Math Problems increases.

Tables of 2 to 10 are the most basic ones and play a crucial role in performing the arithmetic operations. If you are strong enough with the Math Tables of 2 to 10 you can recall or memorize the Tables from 11 to 20 much simply. It helps you to solve complex problems too easily and can save you a great deal of time. Thus, you are advised to learn them by heart so that you can do fundamental estimations.

While learning the Math Tables you will get to see some examples like 4×5 = 20, 5×4 = 20. On seeing such examples you can get to know the patterns and understand the logic like a number multiplied by another number will result in the same product if the numbers are multiplied the other way.

Table of 6 to 10

Table of 11 to 15

Table of 16 to 20

Important Points to Remember Regarding the Math Tables 1 to 20

Below are the key points to be remembered regarding the Multiplication Tables One to Twenty. They are as under

• Each and Every Number in the Multiplicaton Table from 1 to 20 is a Whole Number.
• A number multiplied by itself results in the square of a number.
• Adding a number n times is the same as multiplying it with n. Adding 5 10 times is the same as multiplying 5 by 10 and gives the result 50.

Multiplication Table Chart

Below is the Multiplication Chart for Tables 1 to 10. They are in the following fashion

Benefits of learning Multiplication Table Charts for 1 to 20

Learning Maths Multiplication Tables 1 to 20 provides numerous advantages and boosts your learning abilities. Some of them are outlined as follows

• Helps you to solve math problems much quicker.
• You can avoid mistakes while doing calculations in mind.
• Reciting 1 to 20 Multiplication Tables helps you to understand the patterns among multiples of a number.

Printable Multiplication Tables for 1 to 20 PDF Download

For the sake of your comfort, we have provided the Maths Times Tables from 1 to 20 via quick links available. Simply, tap on them and learn entirely regarding the particular table in no time.

FAQs on Multiplication Tables

1. How do you memorize multiplication tables up to 20?

The fastest way to memorize the Multiplication Tables from 1 to 20 is to master the tips & tricks for each and individual table accordingly. Another way to remember the Tables is through Addition. The number of times a number is multiplied by another number it means that it has been added to itself for the same number of times. For Example, 3 Times 3 is 3+3+3

2. How to Learn Math Tables easily?

Prepare a Multiplication Chart for each and every table and paste it on your walls of the room and try to recite it regularly so that you can remember them for a long time.

3. Why is it important to Learn Multiplication Tables?

• Students are advised to learn Math Tables to perform their mental math calculations quickly.
• Enhances your Problem Solving Abilities and helps you to solve math problems much faster.
• Boosts your arithmetic capabilities of a student.

Properties of Division definition is here. Check the formulae, various properties of division, and how they work on various problems. Know the basics regarding the division and also the division property of equality. Follow the various operators with examples and concepts. Get the expression form and also step by step procedure to solve the problems. Division rule follows many properties and those are important in solving various problems. Check the below sections to know the complete details regarding properties of division, formulae, rules, examples, etc.

Also, Read:

• Properties of Subtraction
• Properties of Multiplication

Properties of Division

Of the four basic arithmetic operations, the division is the one. In the operation of division, we distribute or share the number or a group of things into equal parts. Division operation defines the fair result of sharing. It is the inverse property of multiplication. Division operation has five properties which are discussed in the below sections. The division is defined as the most complicated part of the arithmetic functions. But will be easy if you have a clear idea of all the methods, concepts, rules, and formulae along with a clear understanding of its usage.

Representation of Division Operator

The notation of the division operator is a short horizontal line with 2 dots one above the line and the other below the line.

Notation:

The division is represented with the notation “÷”

Basic Terms Used in Division

Various parts involving in the division rule have a special name.

Dividend – Dividend is the term that is being divided.

Divisor – The term which is being divided by the dividend is called the divisor

Quotient – The term quotient is defined as the result that is obtained in the division process

Remainder – The term remainder is defined as the leftover portion after the division process

Rules of Division

• The first division rule is when the number is divided by zero, then the result is always 0. For suppose, 0 ÷ 4 = 0, i.e., 0 chocolates are shared among 4 pupils and each one gets 0 chocolates.
• No number can be divided with zero, the result gives the undefined value. For suppose, 4 ÷ 0. You have 4 chocolates but no pupil to distribute it, hence you cannot divide it by 0.
• On dividing the number with 1, the result is the same number with which you are dividing. For suppose, 4 ÷ 1 = 4. 4 chocolates divided among one pupil.
• If you divide the number by 2, it means that you are halving the number. For suppose, 4 ÷ 2 = 2. 4 chocolates dividing among two pupils, each gets 2 chocolates.
• On dividing the same number, the result value will always be one. For suppose, 4 ÷ 4 = 1. If 4 chocolates are divided among 4 pupils, then each gets one chocolate.
• The dividend rule must be applied in a proper way because if we interchange the numbers, the result value changes. For suppose, 20 ÷ 4 = 5 and 4 ÷ 20 = 0.2. Hence, the division rule must be applied in the correct order.
• The fractions like ¼, ½, ¾ are known as the division sums. ¼ is nothing but 1 ÷ 4, i.e., 1 chocolate is divided among 4 pupils.

Division Properties

There are various properties of a division operation. They are explained in detail by considering few examples and they are as under

Closure Property

In general closure property states that, the resultant value will be always an integer. But when it comes to the division operation, the resultant value of the division need not be an integer value always. Hence, division fundamental operation does not follow closure property. i.e., a ÷ b is not an integer always. Therefore a ÷ b does not follow closure property.

Example: 7 ÷ 3 is not an integer

If we divide 7 with 3, then the resultant value is 2.33 which is not an integer. Thus, it is proved that closure property is not applicable for division operation.

Commutative Property

In general commutative property states that, even after swapping or shifting of numbers, the resultant value will be the same. When it comes to division operation, it gives the different resultant value when the operators are shifted or swapped. Hence, division operation does not follow the commutative property. i.e., a ÷ b ≠ b ÷ a. Therefore, a ÷ b does not follow the commutative property.

Example: 10 ÷ 5 ≠ 5 ÷ 10

If we divide 7 with 3, the resultant value is 2.33. If we divide 3 with 7, the resultant value is 0.42. Therefore, both the values are not equal. Thus, it is proved that commutative property is not applicable for division operation.

Associative Property

In general associative property states that, even if the parentheses of the expression are rearranged, the resultant will not be changed. When it comes to the division operation, it gives a different value when the parentheses are rearranged. Hence, division operation does not follow the associative property. i.e., a ÷ (b ÷ c) ≠ (a ÷ b) ÷ c. Therefore, a ÷ (b ÷ c) does not follow the associative property.

Example: (16 ÷ 4) ÷ 2 ≠ 16 ÷ (4 ÷ 2)

If we solve (16 ÷ 4) ÷ 2, the resultant value is 2 and if we solve 16 ÷ (4 ÷ 2), the resultant value is 8. Therefore, both the values are not the same. Thus, it is proved that associative property is not applicable for division operation.

Distributive Property

In general distributive property states that, the resultant value is the same, even if the sum of two or more addends are multiplied or each addend multiplied separately, and then the products to be added together. When it comes to division operation, it gives different results when the addends are multiplied separately. Hence, division operation does not follow the distributive property. Therefore a ÷ (b + c) ≠ (a ÷ b) + (a ÷ c).

Example: 12 ÷ (4+ 2) ≠ (12 ÷ 4) + (12 ÷ 2)

If we solve the equation 12 ÷ (4+ 2), we get the resultant value as 2 and if we solve the equation (12 ÷ 4) + (12 ÷ 2), we get the resultant value as 9. Therefore, both the values are not similar. Thus, it is proved that commutative property is not applicable for division operation.

Division by 1

Any number that is divided by 1 gives the resultant value as the same number.

Example: 

5 ÷ 1 = 5

Example Problems on Division Properties

Problem 1: 

There are 80 chocolates. Each packet must be packed with 5 chocolates. How many packets do we need in total?

Solution:

Total number of chocolates = 80

Toffees that are to be packed in 1 packet = 5

Packets needed to pack 80 toffees = 80 ÷ 5

= 16

Therefore, we require 16 packets to pack 80 chocolates

Problem 2:

There are 100 donuts. They are equally packed in 10 packets. How many donuts are there in each box?

Solution:

Total number of donuts = 100

Total number of packets = 10

Number of donuts in each packet = 100 ÷ 10

= 10

Therefore, there are 10 donuts in each box

Problem 3:

50 bottles are placed in 5 equal trays. Find the number of bottles in each tray?

Solution:

Total no of bottles = 50

No of trays = 5

Number of bottles in each tray = 50 ÷ 5

= 10

Therefore, there are 10 bottles in each tray

Students who are searching to get Math Relation problems can check the Worksheet on Math Relation. Our Math Relation Worksheets available improves your preparation level and are very helpful in your practice. It included various models of questions on Math Relations. Therefore, practice all the given examples and check out the answers to cross-check your method of solving. Practice different questions related to Ordered Pair, Cartesian Product of Two Sets, Relation, Domain, and Range of a Relation in Math Relation Worksheet.

See More: Sets

Relations and Functions Questions and Answers

1. Find the values of x and y, if (x + 4, y – 8) = (8, 1).

2. If (x/5 + 3, y – 5/7) = (4, 5/14), find the values of x and y.

3. If X = {m, n, o} and Y = {u, v}, find X × Y and Y × X. Are the two products equal?

4. If P × Q = {(x, 7); (x, 9); (y, 7); (y, 9); (z, 7); (z, 9)}, find P and Q.

5. If M and N are two sets, and M × N consists of 6 elements: If three elements of M × N are (8, 4) (7, 3) (6, 3). Find M × N.

6. If A × B = {(m, 3); (m, 7); (m, 4); (n, 3); (n, 7); (n, 4)}, find B × A.

7. If P = { 2, 1, 9} and Q = {4, 5}, then
Find: (i) P × Q (ii) Q × P (iii) P × P (iv) (Q × Q)

8. If P = {3, 5, 7} and Q = {2, 3, 6}, state which of the following is a relation from P to Q.
(a) R₁ = {(3, 5); (6, 7); (7, 2)} (b) R₂ = {(3, 3); (7, 6)}
(c) R₃ = {(3, 2); (5, 6); (6, 7)} (d) R₄ = {(7, 2); (7, 6); (5, 3); (3, 3), (5, 2), (5, 7)}

9. Write the domain and range of the following relations.
(a) R₁ = {(5, 4); (7, 9); (5, 9); (1, 8); (8, 6); (1, 9)}
(b) R₂ = {(p, 3); (q, 4); (r, 3); (p, 4); (s, 5); (q, 5)}

10. Let P = {3, 4, 5, 6, 7, 8}. Define a relation R from A to A by R = {(x, y) : y = x + 1}.

• Depict this relation using an arrow diagram.
• Write down the domain and range of R.

11. Adjoining figure shows a relationship between the set P and Q. Write this relation in the roster form. What are its domain and range?

12. In the given ordered pairs (2, 4); (4, 16); (5, 7); (1, 3); (6, 36); (2, 9); (1, 1), find the following relationship:
(a) Is a factor of ….
(b) Is a square root of …..
Also, find the domain and range in each case.

13. Draw the arrow diagrams to represent the following relations.
(a) R₁ = {(2, 2); (2, 7); (2, 8); (6, 9); (7, 4)}
(b) R₂ = {(5, 11); (5, 14); (5, 17); (6, 14); (7, 17)}
(c) R₃ = {(3, 4); (4, 6); (5, 8); (6, 10); (7, 12)}
(d) R₄ = {(a, x); (a, y); (b, p); (b, z); (c, y)}

14. Represent the following relation in the roster form.
(a)
(b)
(c)
(d)

Standard Sets of Numbers mean the set of common numbers. As we all know, a set is a collection of well-defined objects. Those well-defined objects can be all numbers also. Based on the elements present in the set, we will call them with some names. Let us check the following sections to know the generally used standard common number sets with examples. Students can also clear their doubts by reading the frequently asked questions section.

Standard Sets of Numbers

There are several standard sets of common numbers. We can represent those standard sets of numbers using three different forms names statement form, roster form, and set-builder form. All these sets are infinite sets, so it will extend infinitely and has no end number. We have represented all these sets in all three forms with definitions and examples.

1. Natural Numbers:

Natural Numbers are the numbers starting from 1 counting upward.

The set of natural numbers are N = {1, 2, 3, 4, 5, 6, 7, . . . }

The statement form is the set of natural numbers.

The set builder form is { x: x is a counting number starting from 1 }

2. Whole Numbers:

The whole numbers are the natural numbers including 0. It will start from 0.

The set of whole numbers are W = {0, 1, 2, 3, 4, 5, 6, . . .}

The statement form is the set of natural numbers including zero.

The set builder form is { x: x is zero and all-natural numbers }

3. Integers:

integers are the set of whole numbers along with the negative numbers means opposite to the natural numbers.

The set of integers are Z or I = { . . . -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, . . . }

The statement form is the set natural numbers, zero, and negative natural numbers.

The set builder form is Z = { x: x ∈ I}

4. Real Numbers:

Real numbers are also called measuring numbers. It includes all numbers and which can be written as decimals. It can include fractions and irrational numbers in the form of decimals.

The set of real numbers are R = {0.5, 0.25, 0.6, 0.07, 0.8}

The set builder form is { x: x is a decimal}

The statement form is the set of decimals.

5. Rational Numbers:

The rational numbers are the fractional numbers. The numerator and denominator of the fractions are integers. The numerator can be zero but the denominator cannot be 0.

The set of rational numbers are R = {\(\frac { 1 }{ 2 } \), \(\frac { -4 }{ 5 } \), \(\frac { 5 }{ 8 } \)}

The statement form is the set of fractions.

The set builder form is { x: x is a fraction }

6. Even Numbers:

Even numbers are the numbers that are divisible by 2.

The statement form of even numbers is the set of numbers divisible by 2.

The roster form is E = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, . . . }

The set builder form is { x : x is a even number}

7. Odd Numbers:

Odd numbers are the numbers that are not divisible by 2.

The set builder form of odd numbers is { x: x is a number that is not divisible by 2 }

The roster form is O = {1, 3, 5, 7, 9, 11, 13, 15, . . . . }

The statement form is “the set of numbers which are not even”.

8. Prime Numbers:

Prime numbers are the positive integers that have only two factors 1 and that integer itself.

The statement form of the prime numbers is “set of numbers has two factors 1 and the same integer”

The set builder form is P = { x: x is a positive integer has only two factors }

The roster form is P = {1, 2, 3, 5, 7, 11, 13, . . . }

9. Complex Numbers:

Complex numbers are the numbers that can be expressed in the form of a + bi. Here ‘i’ is the imaginary unit.

The statement form is “set of numbers in the form of a + bi”

The roster form is C = {1 +2i, 3 + 4i, 5 + 4i, . . . }

The set builder form is C = { x : x is a number in the form of a + bi }

10. Imaginary Numbers:

The imaginary numbers are the numbers which have square root or imaginary unit.

The statement form is “the set of numbers having either square root or imaginary unit”.

The set builder form is I = {x: x is an imaginary number}

The roster form is I = {√5, 3i, √6, √8, √15, . . . }

Also, Read:

FAQs on Standard Sets of Numbers

1. What are the sets of numbers?

The different sets of numbers are natural numbers, whole numbers, integers, real numbers, rational numbers, irrational numbers, even numbers, odd numbers, complex numbers, imaginary numbers, and prime numbers.

2. What are the 3 ways to describe a set?

The 3 different ways to represent a set are statement form, set builder form, and roster form. The last 2 forms use curly braces. The roster form lists all the set elements. The set builder form uses a property and statement form that describes the set verbally.

3. What are the 4 operations of sets?

The four operations of sets are union, intersection, set difference, the complement of a set, and cartesian product.

4. What are sets and their types?

Set is a collection of well-defined objects. The various types of sets are finite set, infinite set, empty set, singleton set, equal sets, equivalent sets, subset, superset, disjoint sets, proper subset, and universal set.

In mathematics, a set is a collection of well-defined objects. Those objects are called members or elements of a set. The set elements are closed between the curly braces and each element is broken up by a comma. The sets are classified into various types. Interested students can go through the following sections to check useful information on set types. You can see definitions and examples for all sets.

Set Types

Based on the elements on the set, size of the set, and other factors, sets are divided into various types. They are listed here.

• Finite Set
• Null Set
• Infinite set
• Equal Sets
• Singleton Set
• Equivalent Sets
• Subset
• Proper Subset
• Cardinal Number of a set
• Power Set
• Superset
• Disjoint Sets
• Universal Set

Types of Sets

Let us discuss the definition and examples of all types of sets in the below sections.

1. Empty Set

If a set has no elements in it, then it is called the empty set. It is also known as the null set or void set. An empty set is represented by ϕ or {}.

Examples:

A = { x : x is a whole number that is not a natural number, x ≠ 0}

Zero is the only whole number that is not a natural number. If x ≠ 0, then there is no possible value for x. So, A = ϕ.

B = { y : 1 < y < 2, y is a natural number}

We know that a natural number cannot be a decimal. So, set y is a null set.

2. Finite Set

A finite set has a definite number of elements. We can find the size of the finite set easily.

Examples:

C = { x | x is a natural number, 20 > x > 10 }

D = { t, y, p, e, s, o, f, s, e, t, s }

3. Infinite Set

A set that has an infinite number of elements in it is called the infinite set. It is not possible to find the size of an infinite set.

Examples:

E = { x : x is a whole number, x > 50 }

The set of whole numbers greater than 50 are 51, 52, 53, 54, . . . . Therefore, set E is an infinite set.

F = { x | x is an even number and x >2 }

The set of even numbers greater than 2 are 4, 6, 8, 10, 12, 14, 16, 18, 20, . . . Hence, set F is an infinite set.

4. Singleton Set

Singleton set is also known as a unit set. If a set has only one element, then it is called the singleton set. The size of a unit set is always 1.

Examples:

G = {5}

As set G has only one element it is a singleton set.

H = {x : x is whole number but not natural number }

We have only one element which is the whole number, not a natural number i.e 0. So, H is a singleton set.

5. Equal Sets

If two sets contain the same elements, then they are equal sets. There is no need to have the same order of elements in both sets.

Examples:

Let I = {4, 14, 15, 5, 6, 18} and J = {15, 5, 18, 14, 4, 6} are two sets.

Then I = J

Here, two sets have the same elements i.e 4, 5, 6, 14, 15, 18

6. Equivalent Sets

If two sets have the same number of elements, then they are called equivalent sets. Two sets order or cardinality is equal.

Examples:

Let K = {8, 17, 25, 63}, L = {56, 5, 45, 28}

The order of K = n(k) = 4

The order of L = n(L) = 4

So, L and K are equivalent sets.

Let M = {p, o, w, e, r}, N = {1, 5, 6, 8, 12}

n(M) = 5

n(N) = 5

So, M and n are equivalent sets.

7. Subset

A set A is said to be a subset of B if all the elements of A are the elements B. Subset is denoted by the symbol ⊂ and A ⊂ B.

Examples:

If O = {0, 3, 6, 8, 14}, P = {15, 5, 0, 1, 2, 3, 6, 14, 7, 8, 9}

The elements of P are 0, 1, 2, 3, 5, 6, 7, 8, 9, 14, and 15.

The elements of O are 0, 3, 6, 8, and 14.

All the elements of O belong to set P. So, O ⊆ P.

8. Proper Subset

If A, B are two sets, A is called the proper subset of B if A ⊂ B but B ⊃ A i.e A ≠ B. The symbol ⊆ is used to represent the proper subset.

Examples:

Q = {7, 5, 2, 16} and R = {2, 5, 7}

All the elements of R are in Q.

n(R) = 3, n(Q) = 4 and Q ≠ R

So, R ⊆ Q

9. Superset

When set A is a subset of set B, then B is a superset of A and it can be represented as B ⊇ A. The symbol ⊇ means “is a superset of”.

Examples:

Let S = {p, o, w, e, r}, T = {p, o, w, e, r, f, u, l}

Here, S ⊂ T. So, T ⊇ S.

10. Universal Set

A set that has all the elements of other given sets is known as the universal set. The symbol is ∪ or ξ.

Examples:

Let P = {a, b, c, d, h},  V = {x, y, z}, W = {m, n, o , p}

∪ = {a, b, c d, e, f, g h, i, j, k, l, m, n, o, p, q, r, s, t, u, v w, x, y, z}

So, ∪ is the universal set.

11. Disjoint Sets

Two sets A and B are called disjoint sets if they do not have common elements between them. So, the properties of disjoint sets are n(A ∩ B) = { }, n(A U B) = n(A) + n(B)

Examples:

X = {1, 2, 5}, Y = {8, 6, 3}

Here, X and y sets has no common element. So X, Y are disjoint sets.

12. Cardinal Number of a set

The number of different elements in the set is called the cardinal number of a set. It is denoted by n(A).

Examples:

Y = { x : x is a natural number, n >10}

n(Y) = 9

Z = {n, u, m, b, e, r, o, f, e, l, e, m, e, n, t, s}

n(Z) = 16

13. Power Set

The set of all subsets is called the power sets. We know that an empty set is a subset of all sets and every set is a subset of itself.

Examples:

If set A = {1, 8, 15}, then power set of A is P(A) = {ϕ, {8}, {15, 8}, {1, 8}, {1, 15}, (8, 1, 15}, {15}, {1}}

Frequently Asked Questions on Set Types

1. How do you express an empty set?

An empty set has no element. it can be represented as ϕ or { }.

2. What are the two sets that contain the same elements?

If two sets have the same elements, then they are called equal sets. The example is A = {m, a, t, h, e, m, a, t, i, c, s} and B = {a, a, m, m, t, t, h, e, s, i, c}. So, A = B.

3. What is a Subset?

If A and B are two sets, and every element of set A is also an element of set B, then A is called a subset of B and expressed as A ⊂ B. B ⊇ A means B is a superset of A. A ⊆ B means A is a proper subset of B.

Read Similar Articles on Sets