Eureka Math

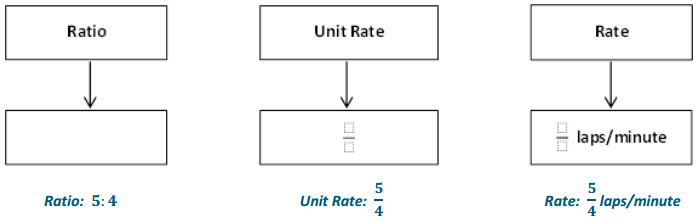
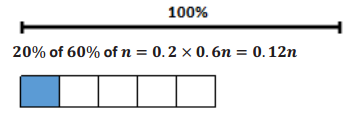
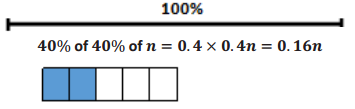
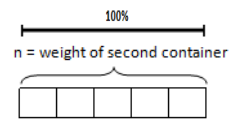
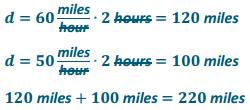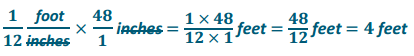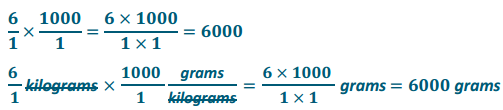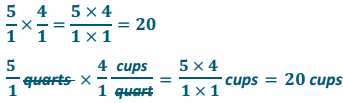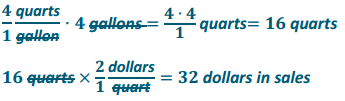Engage NY Eureka Math 6th Grade Module 1 Lesson 20 Answer Key

Eureka Math Grade 6 Module 1 Lesson 20 Example Answer Key

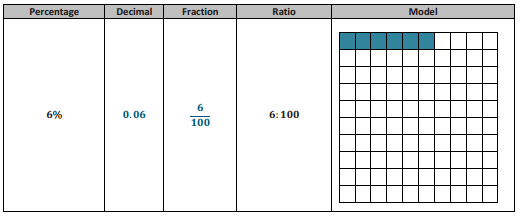
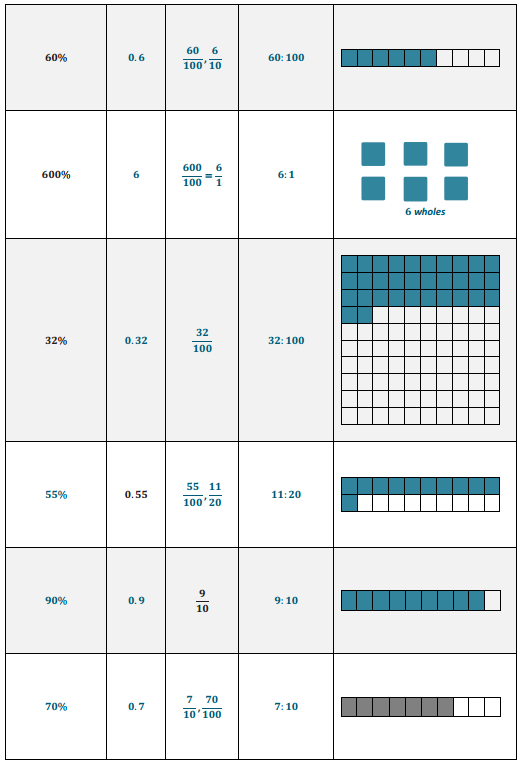
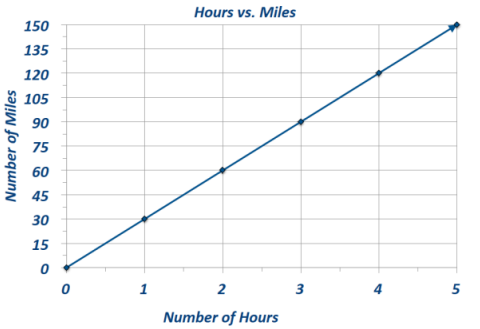
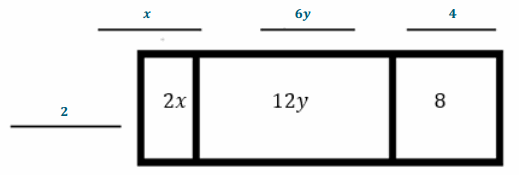
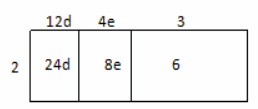
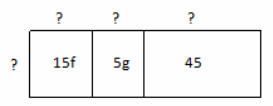
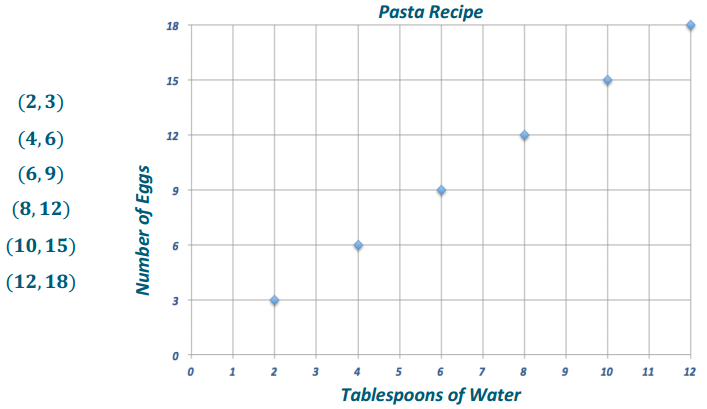
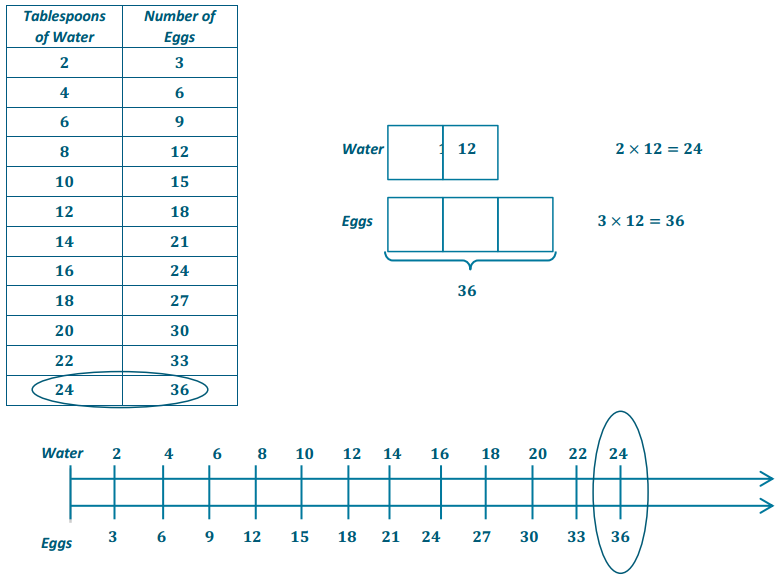
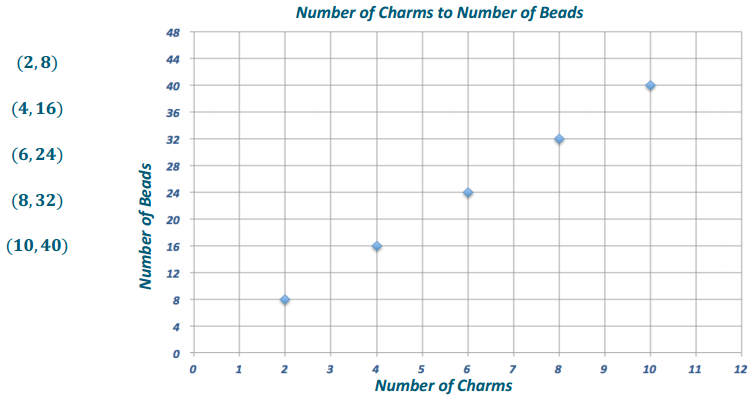
Example 1.
Notes from Exit Ticket
Take notes from the discussion in the space provided below.
Answer:
Notes:

Eureka Math Grade 6 Module 1 Lesson 20 Problem Set Answer Key

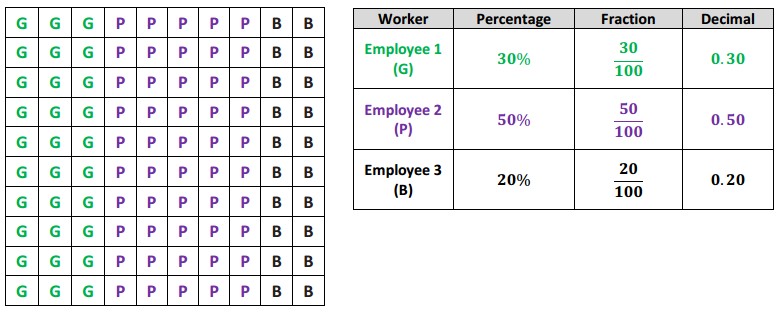
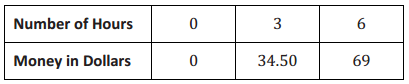
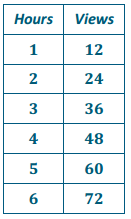
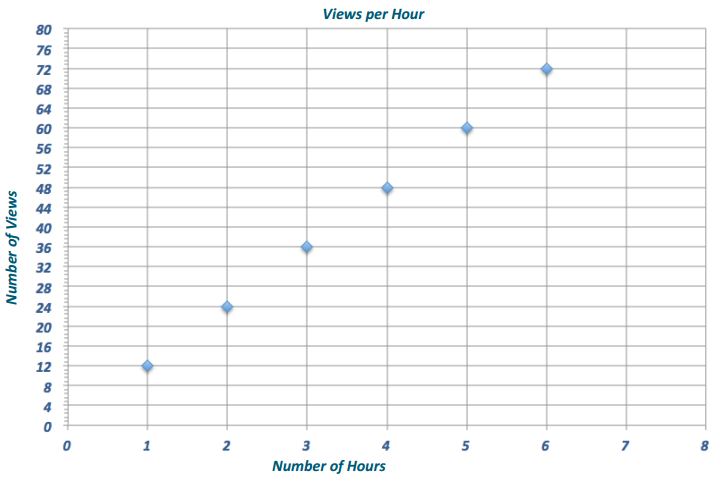
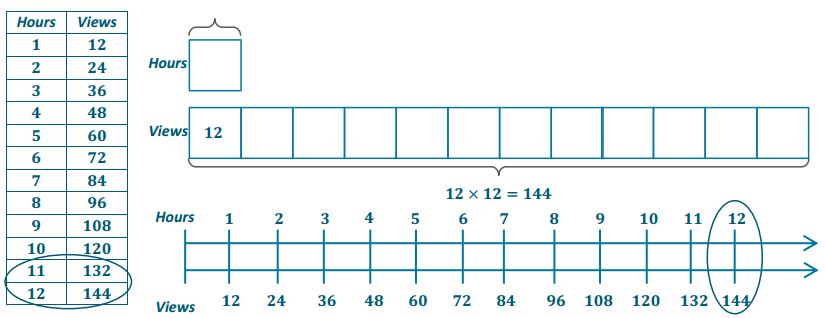
The table below shows the amount of money Gabe earns working at a coffee shop.

Question 1.
How much does Gabe earn per hour?
Answer:
Gabe earns $13. 50 per hour.

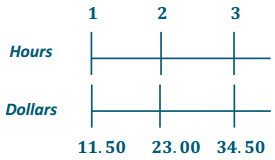
Question 2.
Jordan is another employee at the same coffee shop. He has worked there longer than Gabe and earns $3 more per hour than Gabe. Complete the table below to show how much Jordan earns.

Answer:

Question 3.
Serena is the manager of the coffee shop. The amount of money she earns is represented by the equation m = 21 h, where h is the number of hours Serena works, and m is the amount of money she earns. How much more money does Serena make an hour than Gabe? Explain your thinking.
Answer:
21 – 13.5 = 7.50, so Serena makes $7.50 per hour more than Gabe.

Question 4.
Last month, Jordan received a promotion and became a manager. He now earns the same amount as Serena. How much more money does he earn per hour now that he is a manager than he did before his promotion? Explain your thinking.
Answer:
Jordan now makes the same amount as Serena, which is $21 an hour. Jordan previously made $16.50 an hour, so 21 – 16. 50 = 4.50. Therefore, Jordan will make an additional $4.50 an hour now that he is a manager.

Eureka Math Grade 6 Module 1 Lesson 20 Exit Ticket Answer Key

Question 1.
Value Grocery Mart and Market City are both having a sale on the same popular crackers. McKayla is trying to determine which sale is the better deal. Using the given table and equation, determine which store has the better deal on crackers. Explain your reasoning. (Remember to round your answers to the nearest penny.)
Value Grocery Mart:

Market City:
c = 1. 75b, where c represents the cost in dollars, and b represents the number of boxes of crackers.
Answer:
Value Grocery Mart is better because one box of crackers would cost $1. 67. One box of crackers at Market City would cost $1. 75, which is a little more expensive than Value Grocery Mart.

Eureka Math Grade 6 Module 1 Lesson 20 Exploratory Challenge Answer Key

a. Mallory is on a budget and wants to determine which cereal is a better buy. A 10-ounce box of cereal costs $2.79, and a 13-ounce box of the same cereal costs $3. 99.

i. Which box of cereal should Mallory buy?
Answer:
Because the 10-ounce box costs about 28 cents per ounce, and the 13-ounce box costs about 31 cents per ounce, Mallory should buy the 10-ounce box of cereal.

ii. What is the difference between the two unit prices?
Answer:
The 10-ounce box of cereal would be preferred because it is 3 cents cheaper per ounce.

b. Vivian wants to buy a watermelon. Kingston’s Market has 10-pound watermelons for $3. 90, but the Farmer’s Market has 12-pound watermelons for $4. 44.

i. Which market has the best price for watermelon?
Answer:
The Farmer’s Market has the best price for watermelons.

ii. What is the difference between the two unit prices?
Answer:
The 12-pound watermelon is a better deal because it is 2 cents cheaper per pound.

c. Mitch needs to purchase soft drinks for a staff party. He is trying to figure out if it is cheaper to buy the 12- pack of soda or the 20-pack of soda. The 12-pack of soda costs $3. 99, and the 20-pack of soda costs $5. 48.
i. Which pack should Mitch choose?
Answer:
20-pack of soda for $5.48

ii. What is the difference in cost between single cans of soda from each of the two packs?
Answer:
The difference in cost between single cans from each pack is 6 cents.

d. Mr. Steiner needs to purchase 60 AA batteries. A nearby store sells a 20-pack of AA batteries for $12.49 and a 12-pack of the same batteries for $7. 20.
i. Would it be less expensive for Mr. Steiner to purchase the batteries in 20-packs or 12-packs?
Answer:
He should purchase five 12-packs of batteries for $7.20 for a total cost of $36. 00.

e. The table below shows the amount of calories Mike burns as he runs.

Fill in the missing part of the table.
Answer:

f. Emilio wants to buy a new motorcycle. He wants to compare the gas efficiency for each motorcycle before he makes a purchase. The dealerships presented the data below.

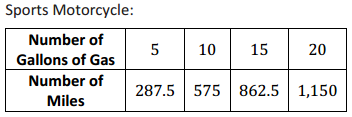
Leisure Motorcycle:

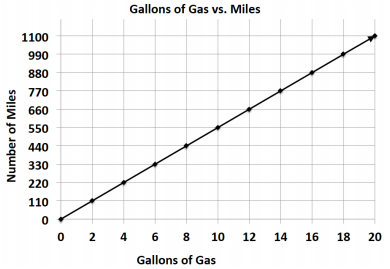
Which motorcycle is more gas efficient and by how much?
Answer:
The sports motorcycle gets 2.5 more miles per gallon of gas.

g. Milton Middle School is planning to purchase a new copy machine. The principal has narrowed the choice to two models: SuperFast Deluxe and Quick Copies. He plans to purchase the machine that copies at the fastest rate. Use the information below to determine which copier the principal should choose.
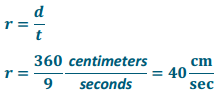
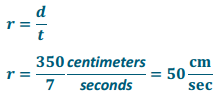
SuperFast Deluxe:

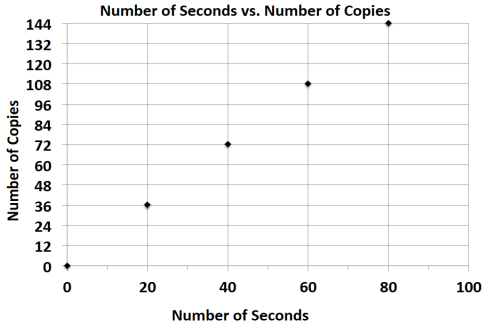
Quick Copies:
c = 1.5t
(where t represents the amount of time in seconds, and C represents the number of copies)
Answer:
SuperFast Deluxe

h. Elijah and Sean are participating In a walk-a-thon. Each student wants to calculate how much money he would make from his sponsors at different points of the walk-a-thon. Use the information in the tables below to determine which student would earn more money if they both walked the same distance. How much more money would that student earn per mile?

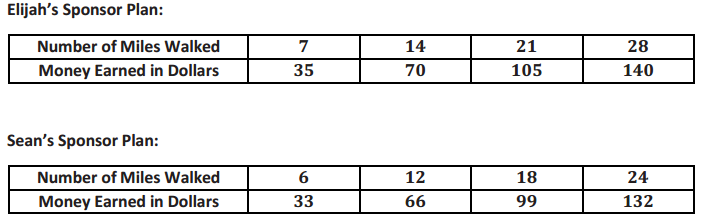
Answer:
Sean earns 50 cents more than Elijah every mile.

i. Gerson is going to buy a new computer to use for his new job and also to download movies. He has to decide between two different computers. How many more kilobytes does the faster computer download in one second?
Choice 1: The rate of download is represented by the following equation: k = 153t, where t represents the amount of time in seconds, and k represents the number of kilobytes.

Choice 2: The rate of download is represented by the following equation: k = 150t, where t represents the amount of time in seconds, and k represents the number of kilobytes.
Answer:
Choice 1 downloads 3 more kilobytes per second than Choice 2.

j. Zyearaye is trying to decide which security system company he will make more money working for. Use the graphs below that show Zyearaye’s potential commission rate to determine which company will pay Zyearaye more commission. How much more commission would Zyearaye earn by choosing the company with the better rate?

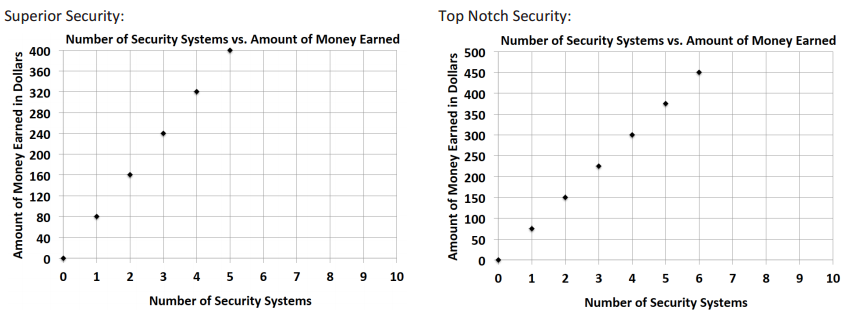
Answer:
Superior Security would pay $5 more per security system sold than Top Notch Security.

k. Emilia and Miranda are sisters, and their mother just signed them up for a new cell phone plan because they send too many text messages. Using the Information below, determine which sister sends the most text messages. How many more text messages does this sister send per week?

Miranda: m = 410w, where w represents the number of weeks, and m represents the number of text messages.
Answer:
Miranda sends 10 more text messages per week than Emilia.

Engage NY Eureka Math 6th Grade Module 1 Lesson 24 Answer Key

Eureka Math Grade 6 Module 1 Lesson 24 Exercise Answer Key

Exercise 1
Robb’s Fruit Farm consists of 100 acres on which three different types of apples grow. On 25 acres, the farm grows Empire apples. Mcintosh apples grow on 30% of the farm. The remainder of the farm grows Fuji apples. Shade in the grid below to represent the portion of the farm each type of apple occupies. Use a different color for each type of apple. Create a key to identify which color represents each type of apple.


Answer:

Exercise 2
The shaded portion of the grid below represents the portion of a granola bar remaining.

What percent does each block of granola bar represent?
Answer:
1% of the granola bar

What percent of the granola bar remains?
Answer:
80%

What other ways can we represent this percent?
Answer:
\(\frac{80}{100}, \frac{8}{10}, \frac{4}{5}, \frac{16}{20}, \frac{32}{40}, \frac{64}{80}, 0.8\)

Exercise 3.

a. For each figure shown, represent the gray shaded region as a percent of the whole figure. Write your answer as a decimal, fraction, and percent.

Answer:

b. What ratio is being modeled in each picture?
Answer:
Picture (a): Answers will vary. One example is the ratio of darker gray to the total is 20 to 100.
Picture (b): 50 to 100, or a correct answer for whichever description they chose.
Picture (c): The ratio of gray to the total Is 48 to 100.

c. How are the ratios and percents related?
Answer:
Answers will vary.

Exercise 4
Each relationship below compares the shaded portion (the part) to the entire figure (the whole). Complete the table.


Answer:

Exercise 5
Mr. Brown shares with the class that 70% of the students got an A on the English vocabulary quiz. If Mr. Brown has 100 students, create a model to show how many of the students received an A on the quiz.
Answer:

70% → \(\frac{70}{100}=\frac{7}{10}\)

What fraction of the students received an A on the quiz?
Answer:
\(\frac{7}{10}\) or \(\frac{70}{100}\)

How could we represent this amount using a decimal?
Answer:
0.7 or 0.70

How are the decimal, the fraction, and the percent all related?
Answer:
The decimal, fraction, and percent all show 70 out of 100.

Exercise 6
Marty owns a lawn mowing service. His company, which consists of three employees, has 100 lawns to mow this week. Use the 10 × 10 grid to model how the work could have been distributed between the three employees.

Answer:
Students choose how they want to separate the workload. The answers will vary. Below is a sample response.

Eureka Math Grade 6 Module 1 Lesson 24 Problem Set Answer Key

Question 1.
Marissa just bought 100 acres of land. She wants to grow apple, peach, and cherry trees on her land. Color the model to show how the acres could be distributed for each type of tree. Using your model, complete the table.

Answer:

Question 2.
After renovations on Kim’s bedroom, only 30 percent of one wall is left without any décor. Shade the grid below to represent the space that is left to decorate.

Answer:

a. What does each block represent?
Answer:
Each block represents \(\frac{1}{100}\) of the total wall.

b. What percent of this wall has been decorated?
Answer:
30%

Eureka Math Grade 6 Module 1 Lesson 24 Exit Ticket Answer Key

Question 1.
One hundred offices need to be painted. The workers choose between yellow, blue, or beige paint. They decide that 45% of the offices will be painted yellow; 28% will be painted blue, and the remaining offices will be painted beige. Create a model that shows the percent of offices that will be painted each color. Write the amounts as decimals and fractions.

Answer:

Engage NY Eureka Math 6th Grade Module 1 Lesson 22 Answer Key

Eureka Math Grade 6 Module 1 Lesson 22 Example Answer Key

Example 1
Walker: Substitute the walker’s distance and time into the equation and solve for the rate of speed.
distance = rate . time
d = r . t

Hint: Consider the units that you want to end up with. If you want to end up with the rate (feet/second), then divide the distance (feet) by time (seconds).

Runner: Substitute the runner’s time and distance into the equation to find the rate of speed.
distance = rate . time
d = r . t
Answer:
Here is a sample of student work using 8 seconds as an example:
d = r . t and r = \(\frac{d}{t}\); Distance: 50 feet; TIme: 8 seconds
r = \(\frac{50}{8} \frac{\mathrm{ft}}{\mathrm{sec}}\) = 6.25 \(\frac{\mathrm{ft}}{\mathrm{sec}}\)

Example 2
Part 1: Chris Johnson ran the 40-yard dash in 4.24 seconds. What is the rate of speed? Round any answer to the nearest hundredth.
distance = rate time
d = r.t
Answer:
d = r.t and r = \(\frac{d}{t}\); r = \(\frac{40}{4.24} \frac{y d}{\sec } \approx 9.43 \frac{y d}{\sec }\)

Part 2: In Lesson 21, we converted units of measure using unit rates. If the runner were able to run at a constant rate, how many yards would he run in an hour? This problem can be solved by breaking it down into two steps. Work with a partner, and make a record of your calculations.
a. How many yards would he run in one minute?
Answer:

b. How many yards would he run in one hour?
Answer:

We completed that problem in two separate steps, but it is possible to complete this same problem in one step. We can multiply the yards per second by the seconds per minute, then by the minutes per hour.

Answer:

Cross out any units that are in both the numerator and denominator in the expression because these cancel each other out.

Part 3: How many miles did the runner travel in that hour? Round your response to the nearest tenth.
Answer:

Cross out any units that are in both the numerator and denominator in the expression because they cancel out.

Eureka Math Grade 6 Module 1 Lesson 22 Exercise Answer Key

Exercise 1.
I drove my car on cruise control at 65 miles per hour for 3 hours without stopping. How far did I go?
d = r.t

Answer:

Cross out any units that are in both the numerator and denominator in the expression because they cancel out. d = ____ miles
Answer:
d = 195 miles

Exercise 2
On the road trip, the speed limit changed to 50 miles per hour in a construction zone. Traffic moved along at a constant rate (50 mph), and it took me 15 minutes (0.25 hours) to get through the zone. What was the distance of the construction zone? (Round your response to the nearest hundredth of a mile.)
d = r t

Answer:

d = 12.50 miles

Eureka Math Grade 6 Module 1 Lesson 22 Problem Set Answer Key

Question 1.
If Adam’s plane traveled at a constant speed of 375 miles per hour for six hours, how far did the plane travel?
Answer:
d = r . t

Question 2.
A Salt March Harvest Mouse ran a 360 centimeter straight course race in 9 seconds. How fast did it run?
Answer:

Question 3.
Another Salt Marsh Harvest Mouse took 7 seconds to run a 350 centimeter race. How fast did it run?
Answer:

Question 4.
A slow boat to China travels at a constant speed of 17.25 miles per hour for 200 hours. How far was the voyage?
Answer:
d = r . t

Question 5.
The Sopwith Camel was a British, First World War, single-seat, biplane fighter introduced on the Western Front in 1917. Traveling at its top speed of 110 mph in one direction for 2\(\frac{1}{2}\) hours, how far did the plane travel?
Answer:
d = r . t

Question 6.
A world-class marathon runner can finish 26.2 miles in 2 hours. What is the rate of speed for the runner?
Answer:

Question 7.
Banana slugs can move at 17 cm per minute. If a banana slug travels for 5 hours, how far will it travel?
Answer:
d = r . t

Eureka Math Grade 6 Module 1 Lesson 22 Exit Ticket Answer Key

Question 1.
Franny took a road trip to her grandmother’s house. She drove at a constant speed of 60 miles per hour for 2 hours. She took a break and then finished the rest of her trip driving at a constant speed of 50 miles per hour for 2 hours. What was the total distance of Franny’s trip?
Answer:

Engage NY Eureka Math 6th Grade Module 1 Lesson 21 Answer Key

Eureka Math Grade 6 Module 1 Lesson 21 Example Answer Key

Example 1.
Work with your partner to find out how many feet are in 48 inches. Make a ratio table that compares feet and inches. Use the conversion rate of 12 inches per foot or \(\frac{1}{12}\) foot per inch.
Answer:

48 inches equals 4 feet

Example 2.
How many grams are in 6 kilograms? Again, make a record of your work before using the calculator. The rate would be 1,000 grams per kg. The unit rate would be 1,000.
Answer:

There are 6,000 grams in 6 kilograms.

Eureka Math Grade 6 Module 1 Lesson 21 Exercise Answer Key

Exercise 1.
How many cups are in 5 quarts? As always, make a record of your work before using the calculator. The rate would be 4 cups per quart. The unit rate would be 4.
Answer:

There are 20 cups in 5 quarts.

Exercise 2.
How many quarts are in 10 cups?
Answer:

Eureka Math Grade 6 Module 1 Lesson 21 Problem Set Answer Key

Question 1.
7 ft. = _________ in.
Answer:
7 ft. =   84    in.

Question 2.
100 yd. = __________ ft.
Answer:
100 yd. =   300    ft.

Question 3.
25 m = _________ cm
Answer:
25 m =   2,500    cm

Question 4.
5 km = _________ m
Answer:
5 km =   5,000    m

Question 5.
96 oz. = ____________ Ib.
Answer:
96 oz. =   6    Ib.

Question 6.
2 mi.= ________ ft.
Answer:
2 mi.=   10.560    ft.

Question 7.
2 mi.= _________ yd.
Answer:
2 mi.=   3,520    yd.

Question 8.
32 fI. oz. = __________ c.
Answer:
32 fI. oz. =    4    c.

Question 9.
1,500 mL = _________ L
Answer:
1,500 mL =   1.5    L

Question 10.
6 g = __________ mg
Answer:
6 g =   6000   mg

Question 11.
Beau buys a 3-pound bag of trail mix for a hike. He wants to make one-ounce bags for his friends with whom he is hiking. How many one-ounce bags can he make?
Answer:
48 bags

Question 12.
The maximum weight for a truck on the New York State Thruway is 40 tons. How many pounds is this?
Answer:
80,000 Ib.

Question 13.
Claudia’s skis are 150 centimeters long. How many meters is this?
Answer:
1. 5m

Question 14.
Claudia’s skis are 150 centimeters long. How many millimeters is this?
Answer:
1, 500 mm

Question 15.
Write your own problem, and solve It. Be ready to share the question tomorrow.
Answer:
Answers will vary.

Eureka Math Grade 6 Module 1 Lesson 21 Exit Ticket Answer Key

Question 1.
Jill and Erika made 4 gallons of lemonade for their lemonade stand. How many quarts did they make? If they charge $2.00 per quart, how much money will they make if they sell it all?
Answer:
The conversion rate is 4 quarts per gallon.

Eureka Math Grade 6 Module 1 Lesson 21 Opening Exercise Answer Key

Identify the ratios that are associated with conversions between feet, inches, and yards.

Question 1.
12 inches = _________ foot; the ratio of inches to feet is _________.
Answer:
12 inches =   1    foot; the ratio of inches to feet is   12: 1   .

Question 2.
1 foot = _________ inches; the ratio of feet to inches is _________.
Answer:
1 foot =   12    inches; the ratio of feet to inches is   1: 12    .

Question 3.
3 feet = ________ yard; the ratio of feet to yards is _________.
Answer:
3 feet =   1    yard; the ratio of feet to yards is   3: 1   .

Question 4.
1 yard = ________ feet; the ratio of yards to feet is _________.
Answer:
1 yard =   3   feet; the ratio of yards to feet is  1: 3   .

Engage NY Eureka Math 7th Grade Module 3 Lesson 20 Answer Key

Eureka Math Grade 7 Module 3 Lesson 20 Example Answer Key

Example 1.
Find the composite area of the shaded region. Use 3.14 for π.

Answer:
Allow students to look at the problem and find the area independently before solving as a class.
→ What information can we take from the image?
Two circles are on the coordinate plane. The diameter of the larger circle is 6 units, and the diameter of the smaller circle is 4 units.

→ How do we know what the diameters of the circles are?
We can count the units along the diameter of the circles, or we can subtract the coordinate points to find the length of the diameter.

→ What information do we know about circles?
The area of a circle is equal to the radius squared times π. We can approximate π as 3.14 or \(\frac{22}{7}\).

→ After calculating the two areas, what is the next step, and how do you know?
The non – overlapping regions add, meaning that the Area(small disk) + Area(ring) = Area(big disk). Rearranging this results in this: Area(ring) = Area(big disk) – Area(small disk). So, the next step is to take the difference of the disks.

→ What is the area of the figure?
9π – 4π = 5π; the area of the figure is approximately 15.7 square units.

Example 2.
Find the area of the figure that consists of a rectangle with a semicircle on top. Use 3.14 for π.

Answer:
A = 28.28 m²
→ What do we know from reading the problem and looking at the picture?
There is a semicircle and a rectangle.

→ What information do we need to find the areas of the circle and the rectangle?
We need to know the base and height of the rectangle and the radius of the semicircle. For this problem, let the radius for the semicircle be r meters.

→ How do we know where to draw the diameter of the circle?
The diameter is parallel to the bottom base of the rectangle because we know that the figure includes a semicircle.

→ What is the diameter and radius of the circle?
The diameter of the circle is equal to the base of the rectangle, 4 m . The radius is half of 4 m, which is 2 m.

→ What would a circle with a diameter of 4 m look like relative to the figure?

→ What is the importance of labeling the known lengths of the figure?
This helps us keep track of the lengths when we need to use them to calculate different parts of the composite figure. It also helps us find unknown lengths because they may be the sum or the difference of known lengths.

→ How do we find the base and height of the rectangle?
The base is labeled 4 m, but the height of the rectangle is combined with the radius of the semicircle. The difference of the height of the figure, 7.5 m, and the radius of the semicircle equals the height of the rectangle. Thus, the height of the rectangle is (7.5 – 2) m, which equals 5.5 m.

→ What is the area of the rectangle?
The area of the rectangle is 5.5 m times 4 m. The area is 22.0 m².

→ What is the area of the semicircle?
The area of the semicircle is half the area of a circle with a radius of 2 m. The area is 4(3.14) m² divided by 2, which equals 6.28 m².

→ Do we subtract these areas as we did in Example 1?
No, we combine the two. The figure is the sum of the rectangle and the semicircle.

→ What is the area of the figure?
28.28 m²

Example 3.
Find the area of the shaded region.

Redraw the figure separating the triangles; then, label the lengths discussing the calculations.
Answer:

→ Do we know any of the lengths of the acute triangle?
No

→ Do we have information about the right triangles?
Yes, because of the given lengths, we can calculate unknown sides.

→ Is the sum or difference of these parts needed to find the area of the shaded region?
Both are needed. The difference of the square and the sum of the three right triangles is the area of the shaded triangle.

→ What is the area of the shaded region?
400 cm² – ((\(\frac{1}{2}\) × 20 cm × 12 cm)+(\(\frac{1}{2}\) × 20 cm × 14 cm) + (\(\frac{1}{2}\) × 8 cm × 6 cm)) = 116 cm²
The area is 116 cm².

Eureka Math Grade 7 Module 3 Lesson 20 Exercise Answer Key

Exercise 1.
A yard is shown with the shaded section indicating grassy areas and the unshaded sections indicating paved areas. Find the area of the space covered with grass in units².

Answer:
Area of rectangle ABCD – area of rectangle IJKL = area of shaded region
(3 ∙ 2) – (\(\frac{1}{2}\) ∙ 1)
6 – \(\frac{1}{2}\)
5 \(\frac{1}{2}\)
The area of the space covered with grass is 5 \(\frac{1}{2}\) units².

Exercise 2.
Find the area of the shaded region. Use 3.14 for π.

Answer:
Area of the triangle + area of the semicircle = area of the shaded region
\(\frac{1}{2}\) b × h) + \(\frac{1}{2}\) )(πr² )
\(\frac{1}{2}\) ∙ 14 cm ∙ 8 cm) + \(\frac{1}{2}\) )(3.14 ∙ (4 cm)² )
56 cm² + 25.12 cm²
81.12 cm²
The area is approximately 81.12 cm².

Exercise 3.
Find the area of the shaded region. The figure is not drawn to scale.

Answer:
Area of squares – (area of the bottom right triangle + area of the top right triangle)
((2 cm × 2 cm)+(3 cm × 3 cm)) – ((\(\frac{1}{2}\) × 5 cm × 2 cm)+(\(\frac{1}{2}\) × 3 cm × 3 cm))
13 cm² – 9.5 cm²
3.5 cm²
The area is 3.5 cm².
There are multiple solution paths for this problem. Explore them with students.

Eureka Math Grade 7 Module 3 Lesson 20 Problem Set Answer Key

Question 1.
Find the area of the shaded region. Use 3.14 for π.

Answer:
Area of large circle– area of small circle
(π × (8 cm)²) – (π × (4 cm)²)
(3.14)(64 cm²) – (3.14)(16 cm²)
200.96 cm² – 50.24 cm²
150.72 cm²
The area of the region is approximately 150.72 cm².

Question 2.
The figure shows two semicircles. Find the area of the shaded region. Use 3.14 for π.

Answer:
Area of large semicircle region – area of small semicircle region = area of the shaded region
(\(\frac{1}{2}\) )(π × (6 cm)²) – (\(\frac{1}{2}\) )(π × (3 cm)²)
(\(\frac{1}{2}\) )(3.14)(36 cm²) – (\(\frac{1}{2}\) )(3.14)(9 cm²)
56.52 cm² – 14.13 cm²
42.39 cm²
The area is approximately 42.39 cm².

Question 3.
The figure shows a semicircle and a square. Find the area of the shaded region. Use 3.14 for π.

Answer:
Area of the square – area of the semicircle
(24 cm × 24 cm) – (\(\frac{1}{2}\) )( π × (12 cm)²)
576 cm² – (\(\frac{1}{2}\) )(3.14 × 144 cm²)
576 cm² – 226.08 cm²
349.92 cm²
The area is approximately 349.92 cm².

Question 4.
The figure shows two semicircles and a quarter of a circle. Find the area of the shaded region. Use 3.14 for π.

Answer:
Area of two semicircles + area of quarter of the larger circle
2(\(\frac{1}{2}\))(π × (5 cm)² ) + (\(\frac{1}{4}\))(π × (10 cm)²)
(3.14)(25 cm² )+(3.14)(25 cm²)
78.5 cm² + 78.5 cm²
157 cm²
The area is approximately 157 cm².

Question 5.
Jillian is making a paper flower motif for an art project. The flower she is making has four petals; each petal is formed by three semicircles as shown below. What is the area of the paper flower? Provide your answer in terms of π.

Answer:
Area of medium semicircle + (area of larger semicircle – area of small semicircle)
(\(\frac{1}{2}\) )(π × (6 cm)² )+((\(\frac{1}{2}\) )(π × (9 cm)² ) – (\(\frac{1}{2}\) )(π × (3 cm)²))
18π cm²+40.5π cm² – 4.5π cm² = 54π cm²
54π cm² × 4
216πcm²
The area is 216π cm².

Question 6.
The figure is formed by five rectangles. Find the area of the unshaded rectangular region.

Answer:
Area of the whole rectangle – area of the sum of the shaded rectangles = area of the unshaded rectangular region
(12 cm × 14 cm) – (2(3 cm × 9 cm) + (11 cm × 3 cm) + (5 cm × 9 cm))
168 cm² – (54 cm² + 33 cm² + 45 cm² )
168 cm² – 132 cm²
36 cm²
The area is 36 cm².

Question 7.
The smaller squares in the shaded region each have side lengths of 1.5 m. Find the area of the shaded region.

Answer:
Area of the 16 m by 8 m rectangle – the sum of the area of the smaller unshaded rectangles = area of the shaded region
(16 m × 8 m) – ((3 m × 2 m) + (4(1.5 m × 1.5 m)))
128 m² – (6 m² + 4(2.25 m² ))
128 m² – 15 m²
113 m²
The area is 113 m².

Question 8.
Find the area of the shaded region.

Answer:
Area of the sum of the rectangles – area of the right triangle = area of shaded region
((17 cm × 4 cm)+(21 cm × 8 cm)) – ((\(\frac{1}{2}\) )(13 cm × 7 cm))
(68 cm²+168 cm² ) – (\(\frac{1}{2}\) )(91 cm² )
236 cm² – 45.5 cm²
190.5 cm²
The area is 190.5 cm².

Question 9.
a. Find the area of the shaded region.

Answer:
Area of the two parallelograms – area of square in the center = area of the shaded region
2(5 cm × 16 cm) – (4 cm × 4 cm)
160 cm² – 16 cm²
144 cm²
The area is 144 cm².

b. Draw two ways the figure above can be divided in four equal parts.
Answer:

c. What is the area of one of the parts in (b)?
Answer:
144 cm² ÷ 4 = 36 cm²
The area of one of the parts in (b) is 36 cm².

Question 10.
The figure is a rectangle made out of triangles. Find the area of the shaded region.

Answer:
Area of the rectangle – area of the unshaded triangles = area of the shaded region
(24 cm × 21 cm) – ((\(\frac{1}{2}\) )(9 cm × 21 cm)+(\(\frac{1}{2}\))(9 cm × 24 cm))
504 cm² – (94.5 cm² + 108 cm² )
504 cm² – 202.5 cm²
301.5 cm²
The area is 301.5 cm².

Question 11.
The figure consists of a right triangle and an eighth of a circle. Find the area of the shaded region. Use \(\frac{22}{7}\) for π.

Answer:
Area of right triangle – area of eighth of the circle = area of shaded region
(\(\frac{1}{2}\))(14 cm × 14 cm) – (\(\frac{1}{8}\))(π × 14 cm × 14 cm)
(\(\frac{1}{2}\))(196 cm²) – (\(\frac{1}{8}\))(\(\frac{22}{7}\))(2 cm × 7 cm × 2 cm × 7 cm)
98 cm² – 77 cm²
21 cm²
The area is approximately 21 cm².

Eureka Math Grade 7 Module 3 Lesson 20 Exit Ticket Answer Key

Question 1.
The unshaded regions are quarter circles. Approximate the area of the shaded region. Use π ≈ 3.14.

Answer:
Area of the square – area of the 4 quarter circles = area of the shaded region
(22 m ∙ 22 m) – ((11 m)² ∙ 3.14)
484 m² – 379.94 m²
104.06 m²
The area of the shaded region is approximately 104.06 m².

Engage NY Eureka Math 6th Grade Module 1 Lesson 19 Answer Key

Eureka Math Grade 6 Module 1 Lesson 19 Example Answer Key

Example 1.
The ratio of cups of blue paint to cups of red paint is 1: 2, which means for every cup of blue paint, there are two cups of red paint. In this case, the equation would be red = 2 × blue, or r = 2b, where b represents the amount of blue paint and r represents the amount of red paint. Make a table of values.
Answer:

Example 2.
Ms. Siple is a librarian who really enjoys reading. She can read \(\frac{3}{4}\) of a book in one day. This relationship can be represented by the equation days = \(\frac{3}{4}\) books, which can be written as d = \(\frac{3}{4}\)b where b represents the number of books and d represents the number of days.
Answer:

Eureka Math Grade 6 Module 1 Lesson 19 Exercise Answer Key

Exercise 1.
Bryan and ShaNiece are both training for a bike race and want to compare who rides his or her bike at a faster rate. Both bikers use apps on their phones to record the time and distance of their bike rides. Bryan’s app keeps track of his route on a table, and ShaNiece’s app presents the information on a graph. The information is shown below.

a. At what rate does each biker travel? Explain how you arrived at your answer.
Answer:

Bryan travels at a rate of 25 miles per hour. The double number line had to be split in 3 equal sections.
That’s how l got25; (25 + 25 + 25) = 75.
ShaNiece travels at 15 miles per hour. I know this by looking at the point (1, 15) on the graph.
The 1 represents the number of hours, and the 15 represents the number of miles.

b. ShaNiece wants to win the bike race. Make a new graph to show the speed ShaNiece would have to ride her bike in order to beat Bryan.
Answer:

The graph shows ShaNiece traveling at a rate of 30 miles per hour, which is faster than Bryan’s rate.

Exercise 2.
Braylen and Tyce both work at a department store and are paid by the hour. The manager told the boys they both earn the same amount of money per hour, but Braylen and Tyce did not agree. They each kept track of how much money they earned in order to determine if the manager was correct. Their data is shown below.

Braylen: m = 10.50h where h represents the number of hours worked and m represents the amount of money Braylen was paid.

Tyce:

a. How much did each person earn in one hour?
Answer:

Tyce earned $11.50 per hour. Braylen earned $10.50 per hour.

b. Was the manager correct? Why or why not?
Answer:
The manager was not correct because Tyce earned $1 more than Braylen in one hour.

Exercise 3.
Claire and Kate are entering a cup stacking contest. Both girls have the same strategy: stack the cups at a constant rate so that they do not slow down at the end of the race. While practicing, they keep track of their progress, which is shown below.

Claire:

Kate: c = 4t, where t represents the amount of time in seconds and c represents the number of stacked cups.
a. At what rate does each girl stack her cups during the practice sessions?
Answer:
Claire stacks cups at a rate of 5 cups per second. Kate stacks cups at a rate of 4 cups per second.

b. Kate notices that she is not stacking her cups fast enough. What would Kate’s equation look like if she wanted to stack cups faster than Claire?
Answer:
Answers will vary. c = 6t, where t represents the time in seconds, and c represents the number of cups stacked.

Eureka Math Grade 6 Module 1 Lesson 19 Problem Set Answer Key

Victor was having a hard time deciding which new vehicle he should buy. He decided to make the final decision based on the gas efficiency of each car. A car that is more gas efficient gets more miles per gallon of gas. When he asked the manager at each car dealership for the gas mileage data, he received two different representations, which are shown below.

Question 1.
If Victor based his decision only on gas efficiency, which car should he buy? Provide support for your answer.
Answer:
Victor should buy the Legend because it gets 18 miles per gallon of gas, and the Supreme only gets 16\(\frac{2}{3}\) miles per gallon. Therefore, the Legend is more gas efficient.

Question 2.
After comparing the Legend and the Supreme, Victor saw an advertisement for a third vehicle, the Lunar. The manager said that the Lunar can travel about 289 miles on a tank of gas. If the gas tank can hold 17 gallons of gas, is the Lunar Victor’s best option? Why or why not?
Answer:
The Lunar is not a better option than the Legend because the Lunar only gets 17 miles per gallon, and the Legend gets 18 miles per gallon. Therefore, the Legend is still the best option.

Eureka Math Grade 6 Module 1 Lesson 19 Exit Ticket Answer Key

Kiara, Giovanni, and Ebony are triplets and always argue over who can answer basic math facts the fastest. After completing a few different math fact activities, Kiara, Giovanni, and Ebony record their data, which is shown below.

Kiara: m = St, where t represents the time in seconds, and m represents the number of math facts completed.

Question 1.
What is the math fact completion rate for each student?
Answer:
Kiara: 5 math facts/second
Giovanni: 4 math facts/second
Ebony: 6 math facts/second

Question 2.
Who would win the argument? How do you know?
Answer:
Ebony would win the argument because when comparing the unit rates of the three triplets, Ebony completes math facts at the fastest rate.

Engage NY Eureka Math 6th Grade Module 1 Lesson 18 Answer Key

Eureka Math Grade 6 Module 1 Lesson 18 Exercise Answer Key

Exercise 1.
Use the table below to write down your work and answers for the stations.

Answer:

Eureka Math Grade 6 Module 1 Lesson 18 Problem Set Answer Key

Question 1.
Enguun earns $17 per hour tutoring student-athletes at Brooklyn University.
a. If Enguun tutored for 12 hours this month, how much money did she earn this month?
Answer:
$204

b. If Enguun tutored for 19. 5 hours last month, how much money did she earn last month?
Answer:
$331.50

Question 2.
The Piney Creek Swim Club is preparing for the opening day of the summer season. The pool holds 22,410 gallons of water, and water is being pumped in at 540 gallons per hour. The swim club has its first practice in 42 hours. Will the pool be full In time? Explain your answer.
Answer:
Yes, the pool will be full of water in time for the first practice because 22,680 gallons of water can be pumped in 42 hours at a rate of 540 gallons per hour. Since 22,680 gallons is more water than the pool needs, we know that the swim club will have enough water.

Eureka Math Grade 6 Module 1 Lesson 18 Exit Ticket Answer Key

Question 1.
Alejandra drove from Michigan to Colorado to visit her friend. The speed limit on the highway is 70 miles/hour. If Alejandra’s combined driving time for the trip was 14 hours, how many miles did Alejandra drive?
Answer:
980 miles

Eureka Math Grade 6 Module 1 Lesson 18 Mathematical Modeling Exercise Answer Key

Question 1.
At Fun Burger, the Burger Master can make hamburgers at a rate of 4 burgers/minute. In order to address the
heavy volume of customers, he needs to continue at this rate for 30 minutes. If he continues to make hamburgers at this pace, how many hamburgers will the Burger Master make in 30 minutes?
Answer:

If the Burger Master can make four burgers in one minute, he can make 120 burgers in 30 minutes.

Question 2.
Chandra is an editor at the New York Gazette. Her job is to read each article before it is printed in the newspaper. If Chandra can read 10 words/second, how many words can she read in 60 seconds?
Answer:

If Chandra can read 10 words in 1 second, then she can read 600 words in 60 seconds.

Engage NY Eureka Math 6th Grade Module 1 Lesson 16 Answer Key

Eureka Math Grade 6 Module 1 Lesson 16 Example Answer Key

Example: Introduction to Rates and Unit Rates
Diet cola was on sale last week; it cost $10 for every 4 packs of diet cola.
a. How much do 2 packs of diet cola cost?
Answer:

2 packs of diet cola cost $5.00.

b. How much does 1 pack of diet cola cost?
Answer:

1 pack of diet cola cost $2.50.

Eureka Math Grade 6 Module 1 Lesson 16 Problem Set Answer Key

The Scott family is trying to save as much money as possible. One way to cut back on the money they spend is by finding deals while grocery shopping; however, the Scott family needs help determining which stores have the better deals.

Question 1.
At Grocery Mart, strawberries cost $2. 99 for 2 lb., and at Baldwin Hills Market strawberries are $3. 99 for 3 lb.
a. What is the unit price of strawberries at each grocery store? If necessary, round to the nearest penny.
Answer:
Grocery Mart: $1.50 per pound (1.495 rounded to the nearest penny)
Baldwin Hills Market: $1.33 per pound

b. If the Scott family wanted to save money, where should they go to buy strawberries? Why?
Answer:
Possible Answer: The Scott family should go to Baldwin Hills Market because the strawberries cost less money there than at Grocery Mart.

Question 2.
Potatoes are on sale at both Grocery Mart and Baldwin Hills Market. At Grocery Mart, a 5 lb. bag of potatoes cost $2.85, and at Baldwin Hills Market a 7 lb. bag of potatoes costs $4. 20. Which store offers the best deal on potatoes? How do you know? How much better is the deal?
Answer:
Grocery Mart: $0. 57 per pound
Baldwin Hills Market: $0.60 per pound
Grocery Mart offers the best deal on potatoes because potatoes cost $0.03 less per pound at Grocery Mart when compared to Baldwin Hills Market.

Eureka Math Grade 6 Module 1 Lesson 16 Exit Ticket Answer Key

Angela enjoys swimming and often swims at a steady pace to burn calories. At this pace, Angela can swim 1, 700 meters in 40 minutes.
a. What is Angela’s unit rate?
Answer:
42.5

b. What is the rate unit?
Answer:
Meters per minute

Eureka Math Grade 6 Module 1 Lesson 16 Exploratory Challenge Answer Key

a. Teagan went to Gamer Realm to buy new video games. Gamer Realm was having a sale: $65 for 4 video games. He bought 3 games for himself and one game for his friend, Diego, but Teagan does not know how much Diego owes him for the one game. What is the unit price of the video games? What is the rate unit?
Answer:
The unit price is $16.25; the rate unit is dollars/video game.

b. Four football fans took turns driving the distance from New York to Oklahoma to see a big game. Each driver set the cruise control during his or her portion of the trip, enabling him or her to travel at a constant speed. The group changed drivers each time they stopped for gas and recorded their driving times and distances in the table below.

Use the given data to answer the following questions.

i. What two quantities are being compared?
Answer:
The two quantities being compared are distance and time, which are measured in miles and hours.

ii. What is the ratio of the two quantities for Andre’s portion of the trip? What is the associated rate?
Answer:
Andre’s ratio: 208:4                Andre’s rate: 52 miles per hour

iii. Answer the same two questions in part (iii) for the other three drivers.
Answer:
Matteo’s ratio: 456:8            Matteo’s rate: 57 miles per hour
Janaye’s ratio: 300:6             Janaye’s rate: 50 miles per hour
Greyson’s ratio: 265:5          Greyson’s rate: 53 miles per hour

iv. For each driver In parts (II) and (III), circle the unit rate, and put a box around the rate unit.
Answer:
If one of these drivers had been chosen to drive the entire distance.
Which driver would have gotten them to the game in the shortest time? Approximately how long would this trip have taken?

c. A publishing company Is looking for new employees to type novels that will soon be published. The publishing company wants to find someone who can type at least 45 words per minute. Dominique discovered she can type at a constant rate of 704 words in 16 minutes. Does Dominique type at a fast enough rate to qualify for the job? Explain why or why not.
Answer:

Dominique does not type at a fast enough rate because she only types 44 words per minute.

Engage NY Eureka Math 6th Grade Module 1 Lesson 17 Answer Key

Eureka Math Grade 6 Module 1 Lesson 17 Example Answer Key

Example 1
Write each ratio as a rate.

a. The ratio of miles to the number of hours is 434 to 7.
Answer:
Miles to hour: 434: 7
Student responses: \(\frac{434}{7} \frac{\text { miles }}{\text { hours }}\) = 62 miles/hour

b. The ratio of the number of laps to the number of minutes is 5 to 4.
Answer:
Laps to minute: 5:4
Student responses: \(\frac{5}{4} \frac{\text { laps }}{\text { minutes }}=\frac{5}{4}\) laps/mm

Example 2.
a. Complete the model below using the ratio from Example 1, part (b).

Answer:

b. Complete the model below now using the rate listed below.

Answer:

Examples 3.
Dave can clean pools at a constant rate of pools/hour.
a. What is the ratio of the number of pools to the number of hours?
Answer:
3: 5

b. How many pools can Dave clean in 10 hours?
Answer:

Dave can clean 6 pools in 10 hours.

c. How long does it take Dave to clean 15 pools?
Answer:

It will take Dave 25 hours to clean 15 pools.

Example 4.
Emeline can type at a constant rate of \(\frac{1}{4}\) pages/minute.
a. What is the ratio of the number of pages to the number of minutes?
Answer:
1: 4

b. Emeline has to type a 5-page article but only has 18 minutes until she reaches the deadline. Does Emeline have enough time to type the article? Why or why not?
Answer:

No, Emeline will not have enough time because It will take her 20 minutes to type a 5-page article.

c. Emeline has to type a 7-page article. How much time will It take her?
Answer:

It will take Emeline 28 minutes to type a 7-page article.

Example 5.
Xavier can swim at a constant speed of \(\frac{5}{3}\) meters/second.
a. What is the ratio of the number of meters to the number of seconds?
Answer:
5: 3

b. Xavier is trying to qualify for the National Swim Meet. To qualify, he must complete a 100-meter race in 55 seconds. Will Xavier be able to qualify? Why or why not?
Answer:

Xavier will not qualify for the meet because he would complete the race in 60 seconds.

c. Xavier is also attempting to qualify for the same meet in the 200-meter event. To qualify, Xavier would have to complete the race in 130 seconds. Will Xavier be able to qualify in this race? Why or why not?
Answer:

Xavier will qualify for the meet in the 200 meter race because he would complete the race in 120 seconds.

Example 6.
The corner store sells apples at a rate of 1. 25 dollars per apple.
a. What is the ratio of the amount in dollars to the number of apples?
Answer:
1.25: 1

b. Akia is only able to spend $10 on apples. How many apples can she buy?
Answer:
8 apples

c. Christian has $6 in his wallet and wants to spend it on apples. How many apples can Christian buy?
Answer:
Christian can buy 4 apples and would spend $5. 00. Christian cannot buy 5 apples because it would cost $6.25, and he only has $6.00.

Eureka Math Grade 6 Module 1 Lesson 17 Problem Set Answer Key

Question 1.
Once a commercial plane reaches the desired altitude, the pilot often travels at a cruising speed. On average, the cruising speed is 570 miles/hour. If a plane travels at this cruising speed for 7 hours, how far does the plane travel while cruising at this speed?
Answer:
3,990 miles

Question 2.
Denver, Colorado often experiences snowstorms resulting in multiple inches of accumulated snow. During the last snow storm, the snow accumulated at \(\frac{4}{5}\) inch/hour. If the snow continues at this rate for 10 hours, how much snow will accumulate?
Answer:
8 inches

Eureka Math Grade 6 Module 1 Lesson 17 Exit Ticket Answer Key

Tiffany is filling her daughter’s pool with water from a hose. She can fill the pool at a rate of \(\frac{1}{10}\) gallons/second. Create at least three equivalent ratios that are associated with the rate. Use a double number line to show your work.
Answer:
Answers will vary.

Engage NY Eureka Math 7th Grade Module 3 Lesson 4 Answer Key

Eureka Math Grade 7 Module 3 Lesson 4 Example Answer Key

Example 1.

Answer:

→ What is happening when you factor and write equivalent expressions for parts (e), (f), (g), and (h)?
→ In the same way that dividing is the opposite or inverse operation of multiplying, factoring is the opposite of expanding.
→ What are the terms being divided by?
→ They are being divided by a common factor.
Have students write an expression that is equivalent to 8x+4.
→ Would it be incorrect to factor out a 2 instead of a 4?

Example 2
Let the variables x and y stand for positive integers, and let 2x, 12y, and 8 represent the area of three regions in the array. Determine the length and width of each rectangle if the width is the same for each rectangle.

Answer:
→ What does 2x represent in the first region of the array?
→ The region has an area of 2x or can be covered by 2x square units.
→ What does the entire array represent?
→ The entire array represents 2x+12y+8 square units.
→ What is the common factor of 2x, 12y, and 8?
→ The common factor of 2x, 12y, and 8 is 2.
→ What are the missing values, and how do you know?
→ The missing values are x, 6y, and 4. If the products are given in the area of the regions, divide the regions by 2 to determine the missing values.

Example 3.
A new miniature golf and arcade opened up in town. For convenient ordering, a play package is available to purchase. It includes two rounds of golf and 20 arcade tokens, plus $3.00 off the regular price. There is a group of six friends purchasing this package. Let g represent the cost of a round of golf, and let t represent the cost of a token. Write two different expressions that represent the total amount this group spent. Explain how each expression describes the situation in a different way.
Answer:
→ What two equivalent expressions could be used to represent the situation?
→ 6(2g+20t-3)
Each person will pay for two rounds of golf and 20 tokens and will be discounted $3.00. This expression is six times the quantity of each friend’s cost.
→ 12g+120t-18
The total cost is equal to 12 games of golf plus 120 tokens, minus $18.00 off the entire bill.

→ What does it mean to take the opposite of a number?
→ You can determine the additive inverse of a number or a multiplicative inverse.
→ What is the opposite of 2?
→ -2
→ What is (-1)(2)?
→ -2
→ What is (-1)(n)?
→ -n
→ What are two mathematical expressions that represent the opposite of (2a+3b)?
→ (-1)(2a+3b) or -(2a+3b)
→ Use the distributive property to write (-1)(2a+3b) as an equivalent expression.
→ -2a-3b or -2a+(-3b)
→ To go from -2a-3b to -(2a+3b), what process occurs?
→ The terms -2a and -3b are written as (-1)(2a) and (-1)(3b), and the -1 is factored out of their sum.

Example 4.
→ What does it mean to take the opposite of a number?
→ You can determine the additive inverse of a number or a multiplicative inverse.
→ What is the opposite of 2?
→ -2
→ What is (-1)(2)?
→ -2
→ What is (-1)(n)?
→ -n
→ What are two mathematical expressions that represent the opposite of (2a+3b)?
→ (-1)(2a+3b) or -(2a+3b)
→ Use the distributive property to write (-1)(2a+3b) as an equivalent expression.
→ -2a-3b or -2a+(-3b)
→ To go from -2a-3b to -(2a+3b), what process occurs?
→ The terms -2a and -3b are written as (-1)(2a) and (-1)(3b), and the -1 is factored out of their sum.

Example 5
Rewrite 5a-(a-3b) in standard form. Justify each step, applying the rules for subtracting and the distributive property.
Answer:
5a+(-(a+-3b)) Subtraction as adding the inverse
5a+(-1)(a+-3b) The opposite of a number is the same as multiplying by –1.
5a+(-1)(a)+(-1)(-3b) Distributive property
5a+-a+3b Multiplying by -1 is the same as the opposite of the number.
4a+3b Collect like terms

Eureka Math Grade 7 Module 3 Lesson 4 Exercise Answer Key

Exercise 1.
Rewrite the expressions as a product of two factors.
a. 72t+8
Answer:
8(9t+1)

b. 55a+11
Answer:
11(5a+1)

c. 36z+72
Answer:
36(z+2)

d. 144q-15
Answer:
3(48q-5)

e. 3r+3s
Answer:
3(r+s)

Exercise 2.
Write the product and sum of the expressions being represented in the rectangular array.
Answer:

2(12d + 4e + 3); 24d + 8e + 6

b. Factor 48j+60k+24 by finding the greatest common factor of the terms.
Answer:
12(4j+5k+2)

Exercise 3.
For each expression, write each sum as a product of two factors. Emphasize the importance of the distributive property. Use various equivalent expressions to justify equivalency.
a. 2∙3+5∙3
Both have a common factor of 3, so the two factors would be 3(2+5). Demonstrate that 3(7) is equivalent to 6+15, or 21.

b. (2+5)+(2+5)+(2+5)
Answer:
This expression is 3 groups of (2+5) or 3(2)+3(5), which is 3(2+5).

c. 2∙2+(5+2)+(5∙2)
Answer:
Rewrite the expression as
2∙2+(5∙2)+(2+5), so 2(2+5)+(2+5), which equals 3(2+5).

d. x∙3+5∙3
Answer:
The greatest common factor is 3, so factor out the 3:

e. 3(x+5). (x+5)+(x+5)+(x+5)
Answer:
Similar to part (b), this is 3 groups of (x+5), so

f. 3(x+5). 2x+(5+x)+5∙2
Answer:
Combine like terms and then identify the common factor. 3x+15, where 3 is the common factor: 3(x+5). Or,
2x+2∙5+(x+5), so that 2(x+5)+(x+5)=3(x+5). Or, use the associative property and write:
2x+(5∙2)+(5+x)
2(x+5)+(5+x)
3(x+5).

g. x∙3+y∙3
Answer:
The greatest common factor is 3, so 3(x+y). (x+y)+(x+y)+(x+y)
There are 3 groups of

h. (x + y) + (x+ y) + (x+y)
Answer:
There are 3 groups of (x+y), so 3(x+y)

i. 2x + (y + x) + 2y
Answer:
Combine like terms and then identify the common factor. 3x+3y, where 3 is the common factor. 3(x+y). Or,
2x+2y+(x+y), so that 2(x+y)+(x+y) is equivalent to 3(x+y). Or, use the associative property, and write:
2x+2y+(y+x)
2(x+y)+(x+y)
3(x+y).

Exercise 4.
a. What is the opposite of (-6v+1)?
Answer:
-(-6v+1)

b. Using the distributive property, write an equivalent expression for part (a).
Answer:
6v-1

Exercise 5.
Expand each expression and collect like terms.
a. -3(2p-3q)
Answer:
-3(2p+(-3q)) Subtraction as adding the inverse
-3∙2p+(-3)∙(-3q) Distributive property
-6p+9q Apply integer rules

b. -a-(a-b)
Answer:
-a+(-(a+-b)) Subtraction as adding the inverse
-1a+(-1(a+-1b)) The opposite of a number is the same as multiplying by –1.
-1a+(-1a)+1b Distributive property
-2a+b Apply integer addition rules

Eureka Math Grade 7 Module 3 Lesson 4 Problem Set Answer Key

Question 1.
Write each expression as the product of two factors.
a. 1∙3+7∙3
Answer:
3(1+7)

b. (1+7)+(1+7)+(1+7)
Answer:
3(1+7)

c. 2∙1+(1+7)+(7∙2)
Answer:
3(1+7)

d. h∙3+6∙3
Answer:
3(h+6)

e. (h+6)+(h+6)+(h+6)
Answer:
3(h+6)

f. 2h+(6+h)+6∙2
Answer:
3(h+6)

g. j∙3+k∙3
Answer:
3(j+k)

h. (j+k)+(j+k)+(j+k)
Answer:
3(j+k)

i. 3(j+k) 2j+(k+j)+2k
Answer:
3(j+k)

Question 2.
Write each sum as a product of two factors.
a. 6∙7+3∙7
Answer:
7(6+3)

b. (8+9)+(8+9)+(8+9)
Answer:
3(8+9)

c. 4+(12+4)+(5∙4)
Answer:
4(1+4+5)

d. 2y∙3+4∙3
Answer:
3(2y+4)

e. (x+5)+(x+5)
Answer:
2(x+5)

f. 3x+(2+x)+5∙2
Answer:
4(x+3)

g. f∙6+g∙6
Answer:
6(f+g)

h. (c+d)+(c+d)+(c+d)+(c+d)
Answer:
4(c+d)

i. 2r+r+s+2s
Answer:
3(r+s)

Question 3.
Use the following rectangular array to answer the questions below.

a. Fill in the missing information.

b. Write the sum represented in the rectangular array.
Answer:
15f + 5g + 45

c. Use the missing information from part (a) to write the sum from part (b) as a product of two factors.
Answer:
5(3f+g+9)

Question 4.
Write the sum as a product of two factors.
a. 81w+48
Answer:
3(27w+16)

b. 10-25t
Answer:
5(2-5t)

c. 12a+16b+8
Answer:
4(3a+4b+2)

Question 5.
Xander goes to the movies with his family. Each family member buys a ticket and two boxes of popcorn. If there are five members of his family, let t represent the cost of a ticket and p represent the cost of a box of popcorn. Write two different expressions that represent the total amount his family spent. Explain how each expression describes the situation in a different way.
Answer:
5(t+2p)
Five people each buy a ticket and two boxes of popcorn, so the cost is five times the quantity of a ticket and two boxes of popcorn.
5t+10p
There are five tickets and 10 boxes of popcorn total. The total cost will be five times the cost of the tickets, plus 10 times the cost of the popcorn.

Question 6.
Write each expression in standard form.
a. -3(1-8m-2n)
Answer:
-3(1+(-8m)+(-2n))
-3+24m+6n

b. 5-7(-4q+5)
Answer:
5+-7(-4q+5)
5+28q+(-35)
28q-35+5
28q-30

c. -(2h-9)-4h
Answer:
-(2h-9)-4h
-(2h+(-9))+(-4h)
-2h+9+(-4h)
-6h+9

d. 6(-5r-4)-2(r-7s-3)
Answer:
6(-5r-4)-2(r-7s-3)
6(-5r+-4)+-2(r-7s+-3)
-30r+-24+-2r+14s+6
-30r+-2r+14s+-24+6
-32r+14s-18

Question 7.
Combine like terms to write each expression in standard form.
a. (r-s)+(s-r)
Answer:
0

b. (-r+s)+(s-r)
Answer:
-2r+2s

c. (-r-s)-(-s-r)
Answer:
0

d. (r-s)+(s-t)+(t-r)
Answer:
0

e. (r-s)-(s-t)-(t-r)
Answer:
2r-2s

Eureka Math Grade 7 Module 3 Lesson 4 Exit Ticket Answer Key

Question 1.
Write the expression below in standard form.
3h-2(1+4h)
Answer:
3h-2(1+4h)
3h+(-2(1+4h)) Subtraction as adding the inverse
3h+(-2∙1)+(-2h∙4) Distributive property
3h+(-2)+(-8h) Apply integer rules
-5h-2 Collect like terms

Question 2.
Write the expression below as a product of two factors.
6m+8n+4
Answer:
The GCF for the terms is 2. Therefore, the factors are 2(3m+4n+2).

Engage NY Eureka Math 6th Grade Module 1 Lesson 15 Answer Key

Eureka Math Grade 6 Module 1 Lesson 15 Exercise Answer Key

Exercise 1.
Create a table to determine how many views the website probably had one hour after the end of the broadcast based on how many views it had two and three hours after the end of the broadcast. Using this relationship, predict how many views the website will have 4, 5, and 6 hours after the end of the broadcast.
Answer:

Exercise 2.
What is the constant number, c, that makes these ratios equivalent?
Answer:
12

Using an equation, represent the relationship between the number of views, y, the website received and the number of hours, h, after this morning’s news broadcast.
Answer:
v = 12h

Exercise 3.
Use the table created In Exercise 1 to Identify sets of ordered pairs that can be graphed.
Answer:
(1, 12), (2,24), (3, 36), (4, 48), (5, 60), (6, 72)

Exercise 4.
Use the ordered pairs you created to depict the relationship between hours and number of views on a coordinate plane.
Label your axes and create a title for the graph. Do the points you plotted lie on a line?

Answer:

Exercise 5
Predict how many views the website will have after twelve hours. Use at least two representations (e.g., tape diagram, table, double number line diagram) to justify your answer.
Answer:

Exercise 6
Also on the news broadcast, a chef from a local Italian restaurant demonstrated how he makes fresh pasta daily for his restaurant. The recipe for his pasta is below:
3 eggs, beaten
1 teaspoon salt
2 cups all-purpose flour
2 tablespoons water
2 tablespoons vegetable oil
Determine the ratio of the number of tablespoons of water to the number of eggs.
Answer:
2: 3

Provided the information in the table below, complete the table to determine ordered pairs. Use the ordered pairs to graph the relationship of the number of tablespoons of water to the number of eggs.

Answer:

Answer:

What would you have to do to the graph in order to find how many eggs would be needed If the recipe was larger and called for 16 tablespoons of water?
Answer:
Extend the graph.

Demonstrate on your graph.

How many eggs would be needed if the recipe called for 16 tablespoons of water?
Answer:
24

Exercise 7.
Determine how many tablespoons of water will be needed If the chef is making a large batch of pasta and the recipe increases to 36 eggs. Support your reasoning using at least one diagram you find applies best to the situation, and explain why that tool is the best to use.
Answer:
Answers may vary but should include reasoning for each tool. For example, extending the table/double number line diagram because values were already given to find the pattern or using a tape diagram to determine the equivalent ratios.

Eureka Math Grade 6 Module 1 Lesson 15 Problem Set Answer Key

Question 1.
The producer of the news station posted an article about the high school’s football championship ceremony on a new website. The website had 500 views after four hours. Create a table to show how many views the website would have had after the first, second, and third hours after posting, if the website receives views at the same rate. How many views would the website receive after 5 hours?
Answer:

Question 2.
Write an equation that represents the relationship from Problem 1. Do you see any connections between the equations you wrote and the ratio of the number of views to the number of hours?
Answer:
125h = v

Question 3.
Use the table in Problem 1 to make a list of ordered pairs that you could plot on a coordinate plane.
Answer:
(1, 125), (2, 250), (3, 375), (4, 500), (5, 625)

Question 4.
Graph the ordered pairs on a coordinate plane. Label your axes and create a title for the graph.
Answer:

Question 5.
Use multiple tools to predict how many views the website would have after 12 hours.
Answer:
Answers may vary but could include all representations from the module. The correct answer is 1,500 views.

Eureka Math Grade 6 Module 1 Lesson 15 Exit Ticket Answer Key

Question 1.
Jen and Nikki are making bracelets to sell at the local market. They determined that each bracelet would have eight beads and two charms.

Complete the table below to show the ratio of the number of charms to the number of beads.

Answer:

Create ordered pairs from the table, and plot the pairs on the graph below. Label the axes of the graph, and provide a title.

Answer:

Eureka Math Grade 6 Module 1 Lesson 15 Exploratory Challenge Answer Key

Question 1.
At the end of this morning’s news segment, the local television station highlighted area pets that need to be adopted. The station posted a specific website on the screen for viewers to find more information on the pets shown and the adoption process. The station producer checked the website two hours after the end of the broadcast and saw that the website had 24 views. One hour after that, the website had 36 views.
Answer:
At the end of this morning’s news segment, the local television station highlighted area pets that need to be adopted. The station posted a specific website on the screen for viewers to find more information on the pets shown and the adoption process. The station producer checked the website two hours after the end of the broadcast and saw that the website had 24 views. One hour after that, the website had 36 views.

Engage NY Eureka Math 7th Grade Module 4 Lesson 16 Answer Key

Eureka Math Grade 7 Module 4 Lesson 16 Example Answer Key

Example 1.
A school has 60% girls and 40% boys. If 20% of the girls wear glasses and 40% of the boys wear glasses, what percent of all students wears glasses?
Answer:
Let n represent the number of students in the school.
The number of girls is 0.6n. The number of boys is 0.4n.

The number of girls wearing glasses is as follows: 0.2(0.6n) = 0.12n.

The number of boys wearing glasses is as follows: 0.4(0.4n) = 0.16n.

The total number of students wearing glasses is 0.12n + 0.16n = 0.28n.
0.28 = 28%, so 28% of the students wear glasses.

Example 2.
The weight of the first of three containers is 12% more than the second, and the third container is 20% lighter than the second. By what percent is the first container heavier than the third container?
Answer:
Let n represent the weight of the second container. (The tape diagram representation for the second container is divided into five equal parts to show 20%. This will be useful when drawing a representation for the third container and also when sketching a 12% portion for the first container since it will be slightly bigger than half of the 20% portion created.)

The weight of the first container is (1.12)n.

The weight of the third container is (0.80)n.

The following represents the difference in weight between the first and third container:
1.12n – 0.80n = 0.32n
Recall that the weight of the third container is 0.8n
0.32n ÷ 0.8n = 0.4. The first container is 40% heavier than the third container.
Or 1.4 × 100% = 140%, which also shows that the first container is 40% heavier than the third container.

Example 3.
In one year’s time, 20% of Ms. McElroy’s investments increased by 5%, 30% of her investments decreased by 5%, and 50% of her investments increased by 3%. By what percent did the total of her investments increase?
Answer:
Let n represent the dollar amount of Ms. McElroy’s investments before the changes occurred during the year.

After the changes, the following represents the dollar amount of her investments:
0.2n(1.05) + 0.3n(0.95) + 0.5n(1.03)
= 0.21n + 0.285n + 0.515n
= 1.01n.

Since 1.01 = 101%, Ms. McElroy’s total investments increased by 1%.

Eureka Math Grade 7 Module 4 Lesson 16 Exercise Answer Key

Exercise 1.
How does the percent of students who wear glasses change if the percent of girls and boys remains the same (that is, 60% girls and 40% boys), but 20% of the boys wear glasses and 40% of the girls wear glasses?
Answer:
Let n represent the number of students in the school.
The number of girls is 0.6n. The number of boys is 0.4n.

Girls who wear glasses:
40% of 60% of n = 0.4 × 0.6n = 0.24n

Boys who wear glasses:

Students who wear glasses:

32% of students wear glasses.

Exercise 2.
How would the percent of students who wear glasses change if the percent of girls is 40% of the school and the percent of boys is 60% of the school, and 40% of the girls wear glasses and 20% of the boys wear glasses? Why?
Answer:
The number of students wearing glasses would be equal to the answer for Example 1 because all of the percents remain the same except that a swap is made between the boys and girls. So, the number of boys wearing glasses is swapped with the number of girls, and the number of girls wearing glasses is swapped with the number of boys, but the total number of students wearing glasses is the same.

Let n represent the number of students in the school.
The number of boys is 0.6n. The number of girls is 0.4n.

Boys who wear glasses:

Girls who wear glasses:

Students who wear glasses:

Exercise 3.
Matthew’s pet dog is 7% heavier than Harrison’s pet dog, and Janice’s pet dog is 20% lighter than Harrison’s. By what percent is Matthew’s dog heavier than Janice’s?
Answer:
Let h represent the weight of Harrison’s dog.
Matthew’s dog is 1.07h, and Janice’s dog is 0.8h.
Since 1.07 ÷ 0.8 = \(\frac{107}{80}\) = 1.3375, Mathew’s dog is 33.75% heavier than Janice’s dog.

Exercise 4.
A concert had 6,000 audience members in attendance on the first night and the same on the second night. On the first night, the concert exceeded expected attendance by 20%, while the second night was below the expected attendance by 20%. What was the difference in percent of concert attendees and expected attendees for both nights combined?
Answer:
Let x represent the expected number of attendees on the first night and y represent the number expected on the second night.

1.2x = 6,000
x = 5,000
6,000 – 5,000 = 1,000
The first night was attended by 1,000 more people than expected.

0.8y = 6,000
y = 7,500
7,500 – 6,000 = 1,500
The second night was attended by 1,500 less people than expected.
5,000 + 7,500 = 12,500
12,500 people were expected in total on both nights.
1,500 – 1,000 = 500. \(\frac{500}{12,500}\) × 100% = 4%. The concert missed its expected attendance by 4%.

Eureka Math Grade 7 Module 4 Lesson 16 Problem Set Answer Key

Question 1.
One container is filled with a mixture that is 30% acid. A second container is filled with a mixture that is 50% acid. The second container is 50% larger than the first, and the two containers are emptied into a third container. What percent of acid is the third container?
Answer:
Let t be the amount of mixture in the first container. Then the second container has 1.5t, and the third container has 2.5t.
The amount of acid in the first container is 0.3t, the amount of acid in the second container is 0.5(1.5t) = 0.75t, and the amount of acid in the third container is 1.05t. The percent of acid in the third container is
\(\frac{1.05}{2.5}\) × 100% = 42%.

Question 2.
The store’s markup on a wholesale item is 40%. The store is currently having a sale, and the item sells for 25% off the retail price. What is the percent of profit made by the store?
Answer:
Let w represent the wholesale price of an item.
Retail price: 1.4w
Sale price: 1.4w – (1.4w × 0.25) = 1.05w
The store still makes a 5% profit on a retail item that is on sale.

Question 3.
During lunch hour at a local restaurant, 90% of the customers order a meat entrée and 10% order a vegetarian entrée. Of the customers who order a meat entrée, 80% order a drink. Of the customers who order a vegetarian entrée, 40% order a drink. What is the percent of customers who order a drink with their entrée?
Answer:
Let e represent lunch entrées.
Meat entrées: 0.9e
Vegetarian entrées: 0.1e
Meat entrées with drinks: 0.9e × 0.8 = 0.72e
Vegetarian entrées with drinks: 0.1e × 0.4 = 0.04e
Entrées with drinks: 0.72e + 0.04e = 0.76e. Therefore, 76% of lunch entrées are ordered with a drink.

Question 4.
Last year’s spell – a – thon spelling test for a first grade class had 15% more words with four or more letters than this year’s spelling test. Next year, there will be 5% less than this year. What percent more words have four or more letters in last year’s test than next year’s?
Answer:
Let t represent this year’s amount of spell – a – thon words with four letters or more.
Last year: 1.15t
Next year: 0.95t
1.15 t ÷ 0.95t × 100% ≈ 121%. There were about 21% more words with four or more letters last year than there will be next year.

Question 5.
An ice cream shop sells 75% less ice cream in December than in June. Twenty percent more ice cream is sold in July than in June. By what percent did ice cream sales increase from December to July?
Answer:
Let j represent sales in June.
December: 0.25j
July: 1.20j
1.20 ÷ 0.25 = 4.8 × 100% = 480%. Ice cream sales in July increase by 380% from ice cream sales in December.

Question 6.
The livestock on a small farm the prior year consisted of 40% goats, 10% cows, and 50% chickens. This year, there is a 5% decrease in goats, 9% increase in cows, and 15% increase in chickens. What is the percent increase or decrease of livestock this year?
Answer:
Let l represent the number of livestock the prior year.
Goats decrease: 0.4l – (0.4l × 0.05) = 0.38l or 0.95(0.4l) = 0.38l
Cows increase: 0.1 l + (0.1l × 0.09 ) = 0.109l or 1.09(0.1l) = 0.109l
Chickens increase: 0.5k + ( 0.5k × 0.15) = 0.575l or 1.15(0.5l) = 0.575l
0.38l + 0.109l + 0.575l = 1.064l. There is an increase of 6.4% in livestock.

Question 7.
In a pet shelter that is occupied by 55% dogs and 45% cats, 60% of the animals are brought in by concerned people who found these animals in the streets. If 90% of the dogs are brought in by concerned people, what is the percent of cats that are brought in by concerned people?
Answer:
Let c represent the percent of cats brought in by concerned people.
0.55(0.9) + (0.45)(c) = 1(0.6)
0.495 + 0.45c = 0.6
0.495 – 0.495 + 0.45c = 0.6 – 0.495
0.45c = 0.105
0.45c ÷ 0.45 = 0.105 ÷ 0.45
c ≈ 0.233
About 23% of the cats brought into the shelter are brought in by concerned people.

Question 8.
An artist wants to make a particular teal color paint by mixing a 75% blue hue and 25% yellow hue. He mixes a blue hue that has 85% pure blue pigment and a yellow hue that has 60% of pure yellow pigment. What is the percent of pure pigment that is in the resulting teal color paint?
Answer:
Let p represent the teal color paint.
(0.75 × 0.85p) + (0.25 × 0.6p) = 0.7875p
78.75% of pure pigment is in the resulting teal color paint.

Question 9.
On Mina’s block, 65% of her neighbors do not have any pets, and 35% of her neighbors own at least one pet. If 25% of the neighbors have children but no pets, and 60% of the neighbors who have pets also have children, what percent of the neighbors have children?
Answer:
Let n represent the number of Mina’s neighbors.
Neighbors who do not have pets: 0.65n
Neighbors who own at least one pet: 0.35n
Neighbors who have children but no pets: 0.25 × 0.65n = 0.1625n
Neighbors who have children and pets: 0.6 × 0.35n = 0.21n
Percent of neighbors who have children: 0.1625n + 0.21n = 0.3725n
37.25% of Mina’s neighbors have children.

Eureka Math Grade 7 Module 4 Lesson 16 Exit Ticket Answer Key

Question 1.
Jodie spent 25% less buying her English reading book than Claudia. Gianna spent 9% less than Claudia. Gianna spent more than Jodie by what percent?
Answer:
Let c represent the amount Claudia spent, in dollars. The number of dollars Jodie spent was 0.75c, and the number of dollars Gianna spent was 0.91c. 0.91c ÷ 0.75c = \(\frac{91}{75}\) × 100% = 121 \(\frac{1}{3}\)%. Gianna spent 21 \(\frac{1}{3}\)% more than Jodie.

Question 2.
Mr. Ellis is a teacher who tutors students after school. Of the students he tutors, 30% need help in computer science and the rest need assistance in math. Of the students who need help in computer science, 40% are enrolled in Mr. Ellis’s class during the school day. Of the students who need help in math, 25% are enrolled in his class during the school day. What percent of the after – school students are enrolled in Mr. Ellis’s classes?
Answer:
Let t represent the after – school students tutored by Mr. Ellis.
Computer science after – school students: 0.3t
Math after – school students: 0.7t

After – school computer science students who are also Mr. Ellis’s students: 0.4 × 0.3t = 0.12t
After – school math students who are also Mr. Ellis’s students: 0.25 × 0.7t = 0.175t

Number of after – school students who are enrolled in Mr. Ellis’s classes: 0.12t + 0.175t = 0.295t
Out of all the students Mr. Ellis tutors, 29.5% of the tutees are enrolled in his classes.

Engage NY Eureka Math 7th Grade Module 3 Lesson 5 Answer Key

Eureka Math Grade 7 Module 3 Lesson 5 Example Answer Key

Example 1.
Write the sum, and then write an equivalent expression by collecting like terms and removing parentheses.
a. 2x and – 2x + 3
Answer:
2x + (- 2x + 3)
(2x + (- 2x)) + 3 Associative property, collect like terms
0 + 3 Additive inverse
3 Additive identity property of zero

b. 2x – 7 and the opposite of 2x
Answer:
2x + (- 7) + (- 2x)
2x + (- 2x) + (- 7) Commutative property, associative property
0 + (- 7) Additive inverse
– 7 Additive identity property of zero

c. The opposite of (5x – 1) and 5x
Answer:
– (5x – 1) + 5x
– 1(5x – 1) + 5x Taking the opposite is equivalent to multiplying by –1.
– 5x + 1 + 5x Distributive property
(- 5x + 5x) + 1 Commutative property, any order property
0 + 1 Additive inverse
1 Additive identity property of zero

Example 2.
• (\(\frac{3}{4}\))×(\(\frac{4}{3}\) )=
Answer:
1

• 4×\(\frac{1}{4}\) =
Answer:
1

• \(\frac{1}{9}\) ×9=
Answer:
1

• (- \(\frac{1}{3}\) )× – 3=
Answer:
1

• (- \(\frac{6}{5}\) )×(- 5/6)=
Answer:
1

→ What are these pairs of numbers called?
→ Reciprocals
→ What is another term for reciprocal?
→ The multiplicative inverse
→ What happens to the sign of the expression when converting it to its multiplicative inverse?
→ There is no change to the sign For example, the multiplicative inverse of – 2 is (- \(\frac{1}{2}\) ) The negative sign remains the same.
→ What can you conclude from the pattern in the answers?
→ The product of a number and its multiplicative inverse is equal to 1.
→ Earlier, we saw that 0 is a special number because it is the only number that when added to another number, results in that number again Can you explain why the number 1 is also special?
→ One is the only number that when multiplied with another number, results in that number again.
→ This property makes 1 special among all the numbers Mathematicians have a special name for 1, the multiplicative identity; they call the property the multiplicative identity property of one.
As an extension, ask students if there are any other special numbers that they have learned Students should respond: Yes; – 1 has the property that multiplying a number by it is the same as taking the opposite of the number Share with students that they are going to learn later in this module about another special number called pi.
As a class, write the product, and then write an equivalent expression in standard form State the properties for each step After discussing questions, review the properties and definitions in the Lesson Summary emphasizing the multiplicative identity property of one and the multiplicative inverse.

Write the product, and then write the expression in standard form by removing parentheses and combining like terms Justify each step.
a. The multiplicative inverse of \(\frac{1}{5}\) and (2x – \(\frac{1}{5}\) )
Answer:
5(2x – \(\frac{1}{5}\) )
5(2x) – 5\(\frac{1}{5}\) Distributive property
10x – 1 Multiplicative inverses

b. The multiplicative inverse of 2 and (2x + 4)
Answer:
(\(\frac{1}{2}\) )(2x + 4)
(\(\frac{1}{2}\) )(2x) + (\(\frac{1}{2}\) )(4) Distributive property
1x + 2 Multiplicative inverses, multiplication
x + 2 Multiplicative identity property of one

c. The multiplicative inverse of (\(\frac{1}{3x + 5}\) ) and \(\frac{1}{3}\)
Answer:
(3x + 5)∙\(\frac{1}{3}\)
3x(\(\frac{1}{3}\) ) + 5(\(\frac{1}{3}\) ) Distributive property
1x + \(\frac{5}{3}\) Multiplicative inverse
x + \(\frac{5}{3}\) Multiplicative identity property of one

Eureka Math Grade 7 Module 3 Lesson 5 Opening Exercise Answer Key

a. In the morning, Harrison checked the temperature outside to find that it was – 12°F Later in the afternoon, the temperature rose 12°F Write an expression representing the temperature change What was the afternoon temperature?
Answer:
– 12 + 12; the afternoon temperature was 0°F.

b. Rewrite subtraction as adding the inverse for the following problems and find the sum.
i. 2 – 2
Answer:
2 + (- 2)=0

ii – 4 – (- 4)
Answer:
(- 4) + 4=0

iii. The difference of 5 and 5
Answer:
5 – 5=5 + (- 5)=0

iv. g – g
g + (- g)=0

c. What pattern do you notice in part (a) and (b)?
Answer:
The sum of a number and its additive inverse is equal to zero.

d. Add or subtract.
i. 16 + 0
Answer:
16

ii. 0 – 7
Answer:
0 + (- 7)= – 7

iii – 4 + 0
– 4

iv. 0 + d
Answer:
d

v. What pattern do you notice in parts (i) through (iv)?
Answer:
The sum of any quantity and zero is equal to the value of the quantity.

e. Your younger sibling runs up to you and excitedly exclaims, “I’m thinking of a number If I add it to the number 2 ten times, that is, 2 + my number + my number + my number, and so on, then the answer is 2 What is my number?” You almost immediately answer, “zero,” but are you sure? Can you find a different number (other than zero) that has the same property? If not, can you justify that your answer is the only correct answer?
Answer:
No, there is no other number On a number line, 2 can be represented as a directed line segment that starts at 0, ends at 2, and has length 2 Adding any other (positive or negative) number v to 2 is equivalent to attaching another directed line segment with length |v| to the end of the first line segment for 2:

If v is any number other than 0, then the directed line segment that represents v will have to have some length, so 2 + v will have to be a different number on the number line Adding v again just takes the new sum further away from the point 2 on the number line.

Eureka Math Grade 7 Module 3 Lesson 5 Exercise Answer Key

Exercise 1
With a partner, take turns alternating roles as writer and speaker The speaker verbalizes how to rewrite the sum and properties that justify each step as the writer writes what is being spoken without any input At the end of each problem, discuss in pairs the resulting equivalent expressions.
Write the sum, and then write an equivalent expression by collecting like terms and removing parentheses whenever possible.
a – 4 and 4b + 4
Answer:
– 4 + (4b + 4)
(- 4 + 4) + 4b Any order, any grouping
0 + 4b Additive inverse
4b Additive identity property of zero

b. 3x and 1 – 3x
Answer:
3x + (1 – 3x)
3x + (1 + (- 3x)) Subtraction as adding the inverse
(3x + (- 3x)) + 1 Any order, any grouping
0 + 1 Additive inverse
1 Additive identity property of zero

c. The opposite of 4x and – 5 + 4x
Answer:
– 4x + (- 5 + 4x)
(- 4x + 4x) + (- 5) Any order, any grouping
0 + (- 5) Additive inverse
– 5 Additive identity property of zero

d. The opposite of – 10t and t – 10t
Answer:
10t + (t – 10t)
(10t + (- 10t)) + t Any order, any grouping
0 + t Additive inverse
t Additive identity property of zero

e. The opposite of (- 7 – 4v) and – 4v
Answer:
– (- 7 – 4v) + (- 4v)
– 1(- 7 – 4v) + (- 4v) Taking the opposite is equivalent to multiplying by –1.
7 + 4v + (- 4v) Distributive property
7 + 0 Any grouping, additive inverse
7 Additive identity property of zero

Exercise 2.
Write the product, and then write the expression in standard form by removing parentheses and combining like terms Justify each step.
a. The reciprocal of 3 and – 6y – 3x
Answer:
(\(\frac{1}{3}\) )(- 6y + (- 3x)) Rewrite subtraction as an addition problem
(\(\frac{1}{3}\) )(- 6y) + (\(\frac{1}{3}\) )(- 3x) Distributive property
– 2y – 1x Multiplicative inverse
– 2y – x Multiplicative identity property of one

b. The multiplicative inverse of 4 and 4h – 20
Answer:
(\(\frac{1}{4}\) )(4h + (- 20)) Rewrite subtraction as an addition problem
(\(\frac{1}{4}\) )(4h) + (\(\frac{1}{4}\) )(- 20) Distributive property
1h + (- 5) Multiplicative inverse
h – 5 Multiplicative identity property of one

c. The multiplicative inverse of – \(\frac{1}{6}\) and 2 – \(\frac{1}{6}\) j
(- 6)(2 + (- \(\frac{1}{6}\) j)) Rewrite subtraction as an addition problem
(- 6)(2) + (- 6)(- \(\frac{1}{6}\) j) Distributive property
– 12 + 1j Multiplicative inverse
– 12 + j Multiplicative identity property of one

Eureka Math Grade 7 Module 3 Lesson 5 Problem Set Answer Key

Question 1.
Fill in the missing parts.
a. The sum of 6c – 5 and the opposite of 6c
(6c – 5) + (- 6c)
_____ Rewrite subtraction as addition
Answer:
(6c + (- 5)) + (- 6c)
6c + (- 6c) + (- 5)
Regrouping/any order (or commutative property of addition)
0 + (- 5) ___
Answer:
Additive inverse
__ Additive identity property of zero
Answer:
– 5

b. The product of – 2c + 14 and the multiplicative inverse of – 2
(- 2c + 14)(- \(\frac{1}{2}\) )
(- 2c)(- \(\frac{1}{2}\) ) + (14)(- \(\frac{1}{2}\) )
Distributive property
__ Multiplicative inverse, multiplication
1c + (- 7)
1c – 7 Adding the additive inverse is the same as subtraction
c – 7 ____
Answer:
Multiplicative identity property of one

Question 2.
Write the sum, and then rewrite the expression in standard form by removing parentheses and collecting like terms.
a. 6 and p – 6
Answer:
6 + (p – 6)
6 + (- 6) + p
0 + p
p

b. 10w + 3 and – 3
Answer:
(10w + 3) + (- 3)
10w + (3 + (- 3))
10w + 0
10w

c – x – 11 and the opposite of – 11
Answer:
(- x + (- 11)) + 11
– x + ((- 11) + (11))
– x + 0
– x

d. The opposite of 4x and 3 + 4x
Answer:
(- 4x) + (3 + 4x)
((- 4x) + 4x) + 3
0 + 3
3

e. 2g and the opposite of (1 – 2g)
Answer:
2g + (- (1 – 2g))
2g + (- 1) + 2g
2g + 2g + (- 1)
4g + (- 1)
4g – 1

Question 3.
Write the product, and then rewrite the expression in standard form by removing parentheses and collecting like terms.
a. 7h – 1 and the multiplicative inverse of 7
Answer:
(7h + (- 1))(\(\frac{1}{7}\) )
(\(\frac{1}{7}\) )(7h) + (\(\frac{1}{7}\) )(- 1)
h – \(\frac{1}{7}\)

b. The multiplicative inverse of – 5 and 10v – 5
(- \(\frac{1}{5}\) )(10v – 5)
(- \(\frac{1}{5}\) )(10v) + (- \(\frac{1}{5}\) )(- 5)
– 2v + 1

Eureka Math Grade 7 Module 3 Lesson 5 Exit Ticket Answer Key

Question 1.
Find the sum of 5x + 20 and the opposite of 20 Write an equivalent expression in standard form Justify each step.
Answer:
(5x + 20) + (- 20)
5x + (20 + (- 20)) Associative property of addition
5x + 0 Additive inverse
5x Additive identity property of zero

Question 2.
For 5x + 20 and the multiplicative inverse of 5, write the product and then write the expression in standard form, if possible Justify each step.
Answer:
(5x + 20)(\(\frac{1}{5}\) )
(5x)(\(\frac{1}{5}\) ) + 20(\(\frac{1}{5}\) ) Distributive property
1x + 4 Multiplicative inverses, multiplication
x + 4 Multiplicative identity property of one

Engage NY Eureka Math 7th Grade Module 3 Lesson 19 Answer Key

Eureka Math Grade 7 Module 3 Lesson 19 Example Answer Key

Example: Area of a Parallelogram
The coordinate plane below contains figure P, parallelogram ABCD.

Answer:

a. Write the ordered pairs of each of the vertices next to the vertex points.
Answer:
See figure.

b. Draw a rectangle surrounding figure P that has vertex points of A and C. Label the two triangles in the figure as S and T.
Answer:
See figure.

c. Find the area of the rectangle.
Answer:
Base = 8 units
Height = 6 units
Area = 8 units × 6 units = 48 sq. units

d. Find the area of each triangle.
Answer:
Figure S
Base = 3 units
Height = 6 units
Area = \(\frac{1}{2}\) × 3 units × 6 units
= 9 sq. units
Figure T
Base = 3 units
Height = 6 units
Area = \(\frac{1}{2}\) × 3 units × 6 units
= 9 sq. units

e. Use these areas to find the area of parallelogram ABCD.
Answer:
Area P = Area of rectangle – Area S – Area T
= 48 sq. units – 9 sq. units – 9 sq. units = 30 sq. units

The coordinate plane below contains figure R, a rectangle with the same base as the parallelogram above.

Answer:

f. Draw triangles S and T and connect to figure R so that you create a rectangle that is the same size as the rectangle you created on the first coordinate plane.
Answer:
See figure.

g. Find the area of rectangle R.
Answer:
Base = 5 units
Height = 6 units
Area = 30 sq. units

h. What do figures R and P have in common?
Answer:
They have the same area. They share the same base and have the same height.

Eureka Math Grade 7 Module 3 Lesson 19 Exercise Answer Key

Exercise 1.
Find the area of triangle ABC.

Answer:
A = \(\frac{1}{2}\) × 7 units × 4 units = 14 sq.units

Exercise 2.
Find the area of quadrilateral ABCD two different ways.

Answer:

\(\frac{1}{2}\) × 2 × 5 + 2 × 5 + \(\frac{1}{2}\) × 1 × 5 = 5 + 10 + 2.5 = 17.5
The area is 17.5 sq.units.

\(\frac{1}{2}\) × (5 + 2) × 5 = 17.5
The area is 17.5 sq.units.

Exercise 3.
The area of quadrilateral ABCD is 12 sq. units. Find x.

Answer:
Area = base×height
12 sq.units = 2x
6 units = x

Exercise 4.
The area of triangle ABC is 14 sq. units. Find the length of side \(\overline{B C}\).

Answer:
Area = \(\frac{1}{2}\) × base×height
14 sq.units = \(\frac{1}{2}\) × BC × (7 units)
BC = 4 units

Exercise 5.
Find the area of triangle ABC.

Answer:
Area of rectangle ARST = 11 units × 10 units = 110 sq.units
Area of triangle ARB = \(\frac{1}{2}\) × 7 units×10 units = 35 sq.units
Area of triangle BSC = \(\frac{1}{2}\) × 4 units×5 units = 10 sq.units
Area of triangle ATC = \(\frac{1}{2}\) × 11 units×5 units = 27.5 sq.units
Area of triangle ABC = Area of ARST – Area of ARB – Area of BSC – Area of ATC = 37.5 sq.units

Eureka Math Grade 7 Module 3 Lesson 19 Problem Set Answer Key

Find the area of each figure.
Question 1.

Answer:
Area = 13.5 sq. units

Question 2.

Answer:
Area = 4.5π sq. units ≈14.13 sq. units

Question 3.

Answer:
Area = 48 sq. units

Question 4.

Answer:
Area = (2π + 16) sq. units ≈ 22.28 sq. units

Question 5.

Answer:
Area = 68 sq. units

Question 6.

Answer:
Area = 46 sq. units

For Problems 7–9, draw a figure in the coordinate plane that matches each description.
Question 7.
A rectangle with an area of 18 sq. units

Answer:

Question 8.
A parallelogram with an area of 50 sq. units

Answer:

Question 9.
A triangle with an area of 25 sq. units

Answer:

Find the unknown value labeled as x on each figure.
Question 10.
The rectangle has an area of 80 sq. units.

Answer:
x = 8

Question 11.
The trapezoid has an area of 115 sq. units.

Answer:
x = 10

Question 12.
Find the area of triangle ABC.

Answer:
Area = 6.5 sq. units

Question 13.
Find the area of the quadrilateral using two different methods. Describe the methods used, and explain why they result in the same area.

Answer:
Area = 15 sq. units
One method is by drawing a rectangle around the figure. The area of the parallelogram is equal to the area of the rectangle minus the area of the two triangles. A second method is to use the area formula for a parallelogram (Area = base × height).

Question 14.
Find the area of the quadrilateral using two different methods. What are the advantages or disadvantages of each method?

Answer:
Area = 60 sq. units
One method is to use the area formula for a trapezoid, A = \(\frac{1}{2}\) (base 1 + base 2)×height. The second method is to split the figure into a rectangle and a triangle. The second method requires more calculations. The first method requires first recognizing the figure as a trapezoid and recalling the formula for the area of a trapezoid.

Eureka Math Grade 7 Module 3 Lesson 19 Exit Ticket Answer Key

The figure ABCD is a rectangle. AB = 2 units, AD = 4 units, and AE = FC = 1 unit.

Question 1.
Find the area of rectangle ABCD.
Answer:
Area = 4 units × 2 units = 8 sq. units

Question 2.
Find the area of triangle ABE.
Answer:
Area = \(\frac{1}{2}\) × 1 unit × 2 units = 1 sq. unit

Question 3.
Find the area of triangle DCF.
Answer:
Area = \(\frac{1}{2}\) × 1 unit × 2 units = 1 sq. unit

Question 4.
Find the area of the parallelogram BEDF two different ways.
Answer:
Area = Area of ABCD – Area of ABE – Area of DCF
= (8 – 1 – 1) sq. units = 6 sq. units

Area = base × height
= 3 units × 2 units = 6 sq. units

Engage NY Eureka Math 7th Grade Module 3 Lesson 18 Answer Key

Eureka Math Grade 7 Module 3 Lesson 18 Example Answer Key

Example 1.
Find the area of the following semicircle. Use π ≈ \(\frac{22}{7}\) .

Answer:
If the diameter of the circle is 14 cm, then the
radius is 7 cm. The area of the semicircle is half
of the area of the circular region.
A ≈ \(\frac{1}{2}\) ∙ \(\frac{22}{7}\) ∙ (7 cm)²
A ≈ \(\frac{1}{2}\) ∙ \(\frac{22}{7}\) ∙ 49 cm²
A ≈ 77 cm²

What is the area of the quarter circle? Use π ≈ \(\frac{22}{7}\) .

Answer:
A ≈ \(\frac{1}{4}\) ∙ \(\frac{22}{7}\) (6 cm)²
A ≈ \(\frac{1}{4}\) ∙ \(\frac{22}{7}\) ∙ 36 cm²
A ≈ \(\frac{198}{7}\) cm²

Example 2.
Marjorie is designing a new set of placemats for her dining room table. She sketched a drawing of the placement on graph paper. The diagram represents the area of the placemat consisting of a rectangle and two semicircles at either end. Each square on the grid measures 4 inches in length.
Find the area of the entire placemat. Explain your thinking regarding the solution to this problem.

Answer:
The length of one side of the rectangular section is 12 inches in length, while the width is 8 inches. The radius of the semicircular region is 4 inches. The area of the rectangular part is (8 in) ∙ (12 in) = 96 in². The total area must include the two semicircles on either end of the placemat. The area of the two semicircular regions is the same as the area of one circle with the same radius. The area of the circular region is A = π ∙ (4 in)² = 16π in². In this problem, using π ≈ 3.14 makes more sense because there are no fractions in the problem. The area of the semicircular regions is approximately 50.24 in². The total area for the placemat is the sum of the areas of the rectangular region and the two semicircular regions, which is approximately (96+50.24) in² = 146.24 in².

If Marjorie wants to make six placemats, how many square inches of fabric will she need? Assume there is no waste.
Answer:
There are 6 placemats that are each 146.24 in², so the fabric needed for all is 6 ∙ 146.24 in² = 877.44 in².

Marjorie decides that she wants to sew on a contrasting band of material around the edge of the placemats. How much band material will Marjorie need?
Answer:
The length of the band material needed will be the sum of the lengths of the two sides of the rectangular region and the circumference of the two semicircles (which is the same as the circumference of one circle with the same radius).
P = (l+l+2πr)
P = (12+12+2 ∙ π ∙ 4) = 49.12
The perimeter is 49.12 in².

Example 3.
The circumference of a circle is 24π cm. What is the exact area of the circle?
Draw a diagram to assist you in solving the problem.

What information is needed to solve the problem?
Answer:
The radius is needed to find the area of the circle. Let the radius be r cm. Find the radius by using the circumference formula.
C = 2πr
24π = 2πr
(\(\frac{1}{2}\) π)24π = (\(\frac{1}{2}\) π)2πr
12 = r
The radius is 12 cm.

Next, find the area.
Answer:
A = π r²
A = π(12)²
A = 144π
The exact area of the circle is 144π cm².

Eureka Math Grade 7 Module 3 Lesson 18 Exercise Answer Key

Opening Exercise
Draw a circle with a diameter of 12 cm and a square with a side length of 12 cm on grid paper. Determine the area of the square and the circle.

Answer:
Area of square: A = (12 cm)² = 144 cm²; Area of circle: A = π ∙ (6 cm)² = 36π cm²

Brainstorm some methods for finding half the area of the square and half the area of the circle.
Answer:
Some methods include folding in half and counting the grid squares and cutting each in half and counting the squares.

Find the area of half of the square and half of the circle, and explain to a partner how you arrived at the area.
Answer:
The area of half of the square is 72 cm². The area of half of the circle is 18π cm². Some students may count the squares; others may realize that half of the square is a rectangle with side lengths of 12 cm and 6 cm and use A = l ∙ w to determine the area. Some students may fold the square vertically, and some may fold it horizontally. Some students will try to count the grid squares in the semicircle and find that it is easiest to take half of the area of the circle.

What is the ratio of the new area to the original area for the square and for the circle?
Answer:
The ratio of the areas of the rectangle (half of the square) to the square is 72:144 or 1:2. The ratio for the areas of the circles is 18π:36π or 1:2.

Find the area of one – fourth of the square and one – fourth of the circle, first by folding and then by another method. What is the ratio of the new area to the original area for the square and for the circle?
Answer:
Folding the square in half and then in half again will result in one – fourth of the original square. The resulting shape is a square with a side length of 6 cm and an area of 36 cm². Repeating the same process for the circle will result in an area of 9π cm². The ratio for the areas of the squares is 36:144 or 1:4. The ratio for the areas of the circles is 9π:36π or 1:4.

Write an algebraic expression that expresses the area of a semicircle and the area of a quarter circle.
Answer:
Semicircle: A = \(\frac{1}{2}\) πr²; Quarter circle: A = \(\frac{1}{4}\) πr²

Exercise 1.
Find the area of a circle with a diameter of 42 cm. Use π ≈ \(\frac{22}{7}\) .
Answer:
If the diameter of the circle is 42 cm, then the radius is 21 cm .
A = πr²
A ≈ \(\frac{22}{7}\) (21 cm)²
A ≈ 1386 cm²

Exercise 2.
The circumference of a circle is 9π cm.
a. What is the diameter?
Answer:
If C = πd, then 9π cm = πd.
Solving the equation for the diameter, d, \(\frac{1}{\pi}\) ∙ 9π cm = \(\frac{1}{\pi}\) π ∙ d.
So, 9 cm = d.

b. What is the radius?
Answer:
If the diameter is 9 cm, then the radius is half of that or \(\frac{9}{2}\) cm.

c. What is the area?
Answer:
The area of the circle is A = π ∙ (\(\frac{9}{2}\) cm)², so A = \(\frac{81}{4}\) π cm².

Exercise 3.
If students only know the radius of a circle, what other measures could they determine? Explain how students would use the radius to find the other parts.
Answer:
If students know the radius, then they can find the diameter. The diameter is twice as long as the radius. The circumference can be found by doubling the radius and multiplying the result by π. The area can be found by multiplying the radius times itself and then multiplying that product by π.

Exercise 4.
Find the area in the rectangle between the two quarter circles if AF = 7 ft, FB = 9 ft, and HD = 7 ft. Use π ≈ \(\frac{22}{7}\) . Each quarter circle in the top – left and lower – right corners have the same radius.

Answer:
The area between the quarter circles can be found by subtracting the area of the two quarter circles from the area of the rectangle. The area of the rectangle is the product of the length and the width. Side AB has a length of 16 ft and Side AD has a length of 14 ft. The area of the rectangle is
A = 16 ft ∙ 14 ft = 224 ft². The area of the two quarter circles is the same as the area of a semicircle, which is half the area of a circle. A = \(\frac{1}{2}\) πr².
A ≈ \(\frac{1}{2}\) ∙ \(\frac{22}{7}\) ∙ (7 ft)²
A ≈ \(\frac{1}{2}\) ∙ \(\frac{22}{7}\) ∙ 49 ft²
A ≈ 77 ft²
The area between the two quarter circles is 224 ft² – 77 ft² = 147 ft².

Eureka Math Grade 7 Module 3 Lesson 18 Problem Set Answer Key

Question 1.
Mark created a flower bed that is semicircular in shape. The diameter of the flower bed is 5 m .
a. What is the perimeter of the flower bed? (Approximate π to be 3.14.)

Answer:
The perimeter of this flower bed is the sum of the diameter and one – half the circumference of a circle with the same diameter.
P = diameter+\(\frac{1}{2}\) π ∙ diameter
P ≈ 5 m+\(\frac{1}{2}\) ∙ 3.14 ∙ 5 m
P ≈ 12.85 m

b. What is the area of the flower bed? (Approximate π to be 3.14.)
Answer:
A = \(\frac{1}{2}\) π (2.5 m)²
A = \(\frac{1}{2}\) π (6.25 m²)
A ≈ 0.5 ∙ 3.14 ∙ 6.25 m²
A ≈ 9.8 m²

Question 2.
A landscape designer wants to include a semicircular patio at the end of a square sandbox. She knows that the area of the semicircular patio is 25.12 cm².
a. Draw a picture to represent this situation.
Answer:

b. What is the length of the side of the square?
Answer:
If the area of the patio is 25.12 cm², then we can find the radius by solving the equation A = \(\frac{1}{2}\) πr² and substituting the information that we know. If we approximate π to be 3.14 and solve for the radius, r, then
25.12 cm² ≈ \(\frac{1}{2}\) πr²
\(\frac{2}{1}\) ∙ 25.12 cm² ≈ \(\frac{2}{1}\) ∙ \(\frac{1}{2}\) πr²
50.24 cm² ≈ 3.14r²
\(\frac{1}{3.14}\) ∙ 50.24 cm² ≈ \(\frac{1}{3.14}\) ∙ 3.14r²
16 cm² ≈ r²
4 cm ≈ r
The length of the diameter is 8 cm; therefore, the length of the side of the square is 8 cm.

Question 3.
A window manufacturer designed a set of windows for the top of a two – story wall. If the window is comprised of 2 squares and 2 quarter circles on each end, and if the length of the span of windows across the bottom is 12 feet, approximately how much glass will be needed to complete the set of windows?

Answer:
The area of the windows is the sum of the areas of the two quarter circles and the two squares that make up the bank of windows. If the span of windows is 12 feet across the bottom, then each window is 3 feet wide on the bottom. The radius of the quarter circles is 3 feet, so the area for one quarter circle window is A = \(\frac{1}{4}\) π ∙ (3 ft)², or A ≈ 7.065 ft². The area of one square window is A = (3 ft)², or 9 ft². The total area is A = 2(area of quarter circle)+2(area of square), or A ≈ (2 ∙ 7.065 ft² )+(2 ∙ 9 ft² ) ≈ 32.13 ft².

Question 4.
Find the area of the shaded region. (Approximate π to be \(\frac{22}{7}\) .)

Answer:
A = \(\frac{1}{4}\) π(12 in)²
A = \(\frac{1}{4}\) π ∙ 144 in²
A ≈ \(\frac{1}{4}\) ∙ \(\frac{22}{7}\) ∙ 144 in²
A ≈ 792/7 in² or 113.1 in²

Question 5.
The figure below shows a circle inside of a square. If the radius of the circle is 8 cm, find the following and explain your solution.

a. The circumference of the circle
Answer:
C = 2π ∙ 8 cm
C = 16π cm

b. The area of the circle
Answer:
A = π ∙ (8 cm)²
A = 64 π cm²

c. The area of the square
Answer:
A = 16 cm ∙ 16 cm
A = 256 cm²

Question 6.
Michael wants to create a tile pattern out of three quarter circles for his kitchen backsplash. He will repeat the three quarter circles throughout the pattern. Find the area of the tile pattern that Michael will use. Approximate π as 3.14.

Answer:
There are three quarter circles in the tile design. The area of one quarter circle multiplied by 3 will result in the total area.
A = \(\frac{1}{4}\) π ∙ (16 cm)²
A ≈ \(\frac{1}{4}\) ∙ 3.14 ∙ 256 cm²
A ≈ 200.96 cm²

A ≈ 3 ∙ 200.96 cm²
A ≈ 602.88 cm²
The area of the tile pattern is approximately 602.88 cm².

Question 7.
A machine shop has a square metal plate with sides that measure 4 cm each. A machinist must cut four semicircles with a radius of \(\frac{1}{2}\) cm and four quarter circles with a radius of 1 cm from its sides and corners. What is the area of the plate formed? Use \(\frac{22}{7}\) to approximate π.

Answer:
The area of the metal plate is determined by subtracting the four quarter circles (corners) and the four half – circles (on each side) from the area of the square. Area of the square: A = (4 cm)² = 16 cm².
The area of four quarter circles is the same as the area of a circle with a radius of
1 cm: A ≈ \(\frac{22}{7}\) (1 cm)² ≈ \(\frac{22}{7}\) cm².
The area of the four semicircles with radius \(\frac{1}{2}\) cm is
A ≈ 4 ∙ \(\frac{1}{2}\) ∙ \(\frac{22}{7}\) ∙ (\(\frac{1}{2}\) cm)²
A ≈ 4 ∙ \(\frac{1}{2}\) ∙ \(\frac{22}{7}\) ∙ \(\frac{1}{4}\) cm² ≈ 11/7 cm².
The area of the metal plate is
A ≈ 16 cm² – \(\frac{22}{7}\) cm² – \(\frac{11}{7}\) cm² ≈ \(\frac{79}{7}\) cm²

Question 8.
A graphic artist is designing a company logo with two concentric circles (two circles that share the same center but have different radii). The artist needs to know the area of the shaded band between the two concentric circles. Explain to the artist how he would go about finding the area of the shaded region.

Answer:
The artist should find the areas of both the larger and smaller circles. Then, the artist should subtract the area of the smaller circle from the area of the larger circle to find the area between the two circles. The area of the larger circle is
A = π ∙ (9 cm)\(\frac{22}{7}\) or 81π cm\(\frac{22}{7}\) .
The area of the smaller circle is
A = π(5 cm)\(\frac{22}{7}\) or 25π cm\(\frac{22}{7}\) .
The area of the region between the circles is 81π cm\(\frac{22}{7}\) – 25π cm\(\frac{22}{7}\) = 56π cm\(\frac{22}{7}\) . If we approximate π to be 3.14, then A ≈ 175.84 cm\(\frac{22}{7}\) .

Question 9.
Create your own shape made up of rectangles, squares, circles, or semicircles, and determine the area and perimeter.
Answer:
Student answers may vary.

Eureka Math Grade 7 Module 3 Lesson 18 Exit Ticket Answer Key

Question 1.
Ken’s landscape gardening business creates odd – shaped lawns that include semicircles. Find the area of this semicircular section of the lawn in this design. Use \(\frac{22}{7}\) for π.

Answer:
If the diameter is 5 m, then the radius is \(\frac{5}{2}\) m. Using the formula for area of a semicircle, A = \(\frac{1}{2}\) πr², A ≈ \(\frac{1}{2}\) ∙ \(\frac{22}{7}\) ∙ (\(\frac{5}{2}\) m)². Using the order of operations,
A ≈ \(\frac{1}{2}\) ∙ \(\frac{22}{7}\) ∙ \(\frac{25}{4}\) m² ≈ \(\frac{550}{56}\) m² ≈ 9.8 m².

Question 2.
In the figure below, Ken’s company has placed sprinkler heads at the center of the two small semicircles. The radius of the sprinklers is 5 ft. If the area in the larger semicircular area is the shape of the entire lawn, how much of the lawn will not be watered? Give your answer in terms of π and to the nearest tenth. Explain your thinking.

Answer:
The area not covered by the sprinklers would be the area between the larger semicircle and the two smaller ones. The area for the two semicircles is the same as the area of one circle with the same radius of 5 ft. The area not covered by the sprinklers can be found by subtracting the area of the two smaller semicircles from the area of the large semicircle.

Area Not Covered = Area of large semicircle – Area of two smaller semicircles
A = \(\frac{1}{2}\) π ∙ (10 ft)² – (2 ∙ (\(\frac{1}{2}\) (π ∙ (5 ft)² )))
A = \(\frac{1}{2}\) π ∙ 100 ft² – π ∙ 25 ft²
A = 50π ft² – 25π ft² = 25π ft²
Let π ≈ 3.14
A ≈ 78.5 ft²
The sprinklers will not cover 25π ft² or 78.5 ft² of the lawn.