Eureka Math

Engage NY Eureka Math 7th Grade Module 4 Mid Module Assessment Answer Key

Eureka Math Grade 7 Module 4 Mid Module Assessment Task Answer Key

Question 1.
In New York, state sales tax rates vary by county. In Allegany County, the sales tax rate is 8 1/2%.
a. A book costs $12.99, and a video game costs $39.99. Rounded to the nearest cent, how much more is the tax on the video game than the tax on the book?
Answer:
12.99(8.5%) = 12.99(0.085) = 1.10415
39.99(8.5%) = 39.99(0.085) = 3.39915
3.39915 – 1.10415 = 2.295
= $ 2.30

b. Using n to represent the cost of an item in dollars before tax and t to represent the amount of sales tax in dollars for that item, write an equation to show the relationship between n and t.
Answer:
t = 0.085 n

c. Using your equation, create a table that includes five possible pairs of solutions to the equation. Label each column appropriately.
Answer:

d. Graph the relationship from parts (b) and (c) in the coordinate plane. Include a title and appropriate scales and labels for both axes.

Answer:

e. Is the relationship proportional? Why or why not? If so, what is the constant of proportionality? Explain.
Answer:
Yes, the relationship is proportional because the graph of the equation is a straight line that touches the origin. Also, the table shows that the ratio of the \(\frac{\text { amount of sales tax }}{\text { cost of an item }}\) equal 0.085.
\(\frac{0.085}{1}=\frac{0.17}{2}=\frac{0.255}{3}=\frac{0.34}{4}=\frac{0.425}{5}\)
The constant of proportionality is 0.085 because that is the sales tax amount for $ 1.00, which is the unit rate.

f. In nearby Wyoming County, the sales tax rate is 8%. If you were to create an equation, graph, and table for this tax rate (similar to parts (b), (c), and (d)), what would the points (0,0) and (1,0.08) represent? Explain their meaning in the context of this situation.
Answer:
The point of origin (0, 0) means that no tax has been applied yet because nothing has been purchased. The point (1, 0.08) is the unit rate, or the constant of proportionality. It means that for an item that costs $ 1.00, the amount of tax applied is $ 0.08. The unit rate also shows that for every 1.00, the amount of tax will increase by $ 0.08.

g. A customer returns an item to a toy store in Wyoming County. The toy store has another location in Allegany County, and the customer shops at both locations. The customer’s receipt shows $2.12 tax was charged on a $24.99 item. Was the item purchased at the Wyoming County store or the Allegany County store? Explain and justify your answer by showing your math work.
Answer:
The item was purchased in allegany county
\(\frac{2.12}{24.99}\) is about, \(\frac{2.12}{25} \times 4\) = \(\frac{8.48}{100}\),
Which is 8.48%, or about 8.5%.

Question 2.
Amy is baking her famous pies to sell at the Town Fall Festival. She uses 32\(\frac{1}{2}\) cups of flour for every 10 cups of sugar in order to make a dozen pies. Answer the following questions below and show your work.
a. Write an equation, in terms of f, representing the relationship between the number of cups of flour used and the number of cups of sugar used to make the pies.
Answer:
f = \(\frac{13}{4}\) S

b. Write the constant of proportionality as a percent. Explain what it means in the context of this situation.
Answer:
3.25 = \(\frac{325}{100}\) = 3.25%
A constant of proportionality of 325% means that the amount of flour used to make the pies is 325% the amount of sugar used.

c. To help sell more pies at the festival, Amy set the price for one pie at 40% less than what it would cost at her bakery. At the festival, she posts a sign that reads, “Amy’s Famous Pies—Only $9.00/Pie!” Using this information, what is the price of one pie at the bakery?
Answer:

The price of one pie at the bakery is $15.00.

Engage NY Eureka Math 7th Grade Module 5 Lesson 23 Answer Key

Eureka Math Grade 7 Module 5 Lesson 23 Example Answer Key

Example 1: Texting
With texting becoming so popular, Linda wanted to determine if middle school students memorize real words more or less easily than fake words. For example, real words are food, car, study, swim; whereas fake words are stk, fonw, cqur, ttnsp. She randomly selected 28 students from all middle school students in her district and gave half of them a list of 20 real words and the other half a list of 20 fake words.

a. How do you think Linda might have randomly selected 28 students from all middle school students in her district?
Answer:
Random selection is done in an attempt to obtain students to represent all middle school students in the district. Linda would need to number all middle school students and use a random device to generate
28 numbers. One device to generate integers is http://www.rossmanchance.com/applets/RandomGen/GenRandom01.htm. Note that if there are duplicates, additional random numbers need to be generated. A second way to generate the random selections is by using the random number table provided in previous lessons.

b. Why do you think Linda selected the students for her study randomly? Explain.
Answer:
Linda randomly assigned her chosen 28 students to two groups of 14 each. Random assignment is done to help ensure that groups are similar to each other.

c. She gave the selected students one minute to memorize their lists, after which they were to turn the lists over and, after two minutes, write down all the words that they could remember. Afterward, they calculated the number of correct words that they were able to write down. Do you think a penalty should be given for an incorrect word written down? Explain your reasoning.
Answer:
Answers will vary. Either position is acceptable. The purpose is to get students to take a position and argue for it.

Example 2.
Ken, an eighth-grade student, was interested in doing a statistics study involving sixth-grade and eleventh-grade students in his school district. He conducted a survey on four numerical variables and two categorical variables (grade level and gender). His Excel population database for the 265 sixth graders and 175 eleventh graders in his district has the following description:

a. Ken decides to base his study on a random sample of 20 sixth graders and a random sample of 20 eleventh graders. The sixth graders have IDs 1–265, and the eleventh graders are numbered 266–440. Advise him on how to randomly sample 20 sixth graders and 20 eleventh graders from his data file.
Answer:
Ken should first number the sixth graders from 1 to 265 and the eleventh graders from 266 to 440. Then, Ken can choose 20 different random integers from 1to 265 for the sixth-grade participants and 20 different random integers from 266 to 440 for the eleventh graders.

Suppose that from a random number generator:
The random ID numbers for Ken’s 20 sixth graders: 231 15 19 206 86 183 233 253 142 36 195 139 75 210 56 40 66 114 127 9
The random ID numbers for his 20 eleventh graders: 391 319 343 426 307 360 289 328 390 350 279 283 302 287 269 332 414 267 428 280

b. For each set, find the homework hours data from the population database that correspond to these randomly selected ID numbers.
Answer:
Sixth graders’ IDs ordered: 9 15 19 36 40 56 66 75 86 114 127 139 142 183 195 206 210 231 233 253
Their data: 8.4 7.2 9.2 7.9 9.3 7.6 6.5 6.7 8.2 7.7 7.7 4.8 5.4 4.7 7.1 6.6 2.9 8.5 6.1 8.6
Eleventh graders’ IDs ordered: 267 269 279 280 283 287 289 302 307 319 328 332 343 350 360 390 391 414 426 428
Their data:
9.5 9.8 10.9 11.8 10.0 12.0 9.1 11.8 10.0 8.3 10.6 9.5 9.8 10.8 10.7 9.4 13.2 7.3 11.6 10.3

c. On the same scale, draw dot plots for the two sample data sets.
Answer:

d. From looking at the dot plots, list some observations comparing the number of hours per week that sixth graders spend on doing homework and the number of hours per week that eleventh graders spend on doing homework.
Answer:
There is some overlap between the data for the two random samples. The sixth-grade distribution may be slightly skewed to the left. The eleventh-grade distribution is fairly symmetric. The mean number of homework hours for sixth graders appears to be around 7 hours, whereas that for the eleventh graders is around 10.

e. Calculate the mean and MAD for each of the data sets. How many MADs separate the two sample means? (Use the larger MAD to make this calculation if the sample MADs are not the same.)

Answer:

The number of MADs that separate the two means is \(\frac{10.32-7.055}{1.274}\), or 2.56.

f. Ken recalled Linda suggesting that if the number of MADs is greater than or equal to 2, then it would be reasonable to think that the population of all sixth-grade students in his district and the population of all eleventh-grade students in his district have different means. What should Ken conclude based on his homework study?
Answer:
Since 2.56 is greater than 2, it is reasonable to conclude that on average eleventh graders spend more time doing homework per week than do sixth graders.

Eureka Math Grade 7 Module 5 Lesson 23 Exercise Answer Key

Exercises 1–4
Suppose the data (the number of correct words recalled) she collected were as follows:
For students given the real words list: 8,11,12,8,4,7,9,12,12,9,14,11,5,10
For students given the fake words list: 3,5,4,4,4,7,11,9,7,7,1,3,3,7

Exercise 1.
On the same scale, draw dot plots for the two data sets.
Answer:

Exercise 2.
From looking at the dot plots, write a few sentences comparing the distribution of the number of correctly recalled real words with the distribution of the number of correctly recalled fake words. In particular, comment on which type of word, if either, that students recall better. Explain.
Answer:
There is a considerable amount of overlap between data from the two random samples. The distribution of the number of real words recalled is somewhat skewed to the left; the distribution of the number of fake words recalled is fairly symmetric. The real words distribution appears to be centered around 9 or 10, whereas the fake words distribution appears to be centered around 6. Whether the separation between 9 and 6 is meaningful remains to be seen. If it is meaningful, then the mean number of real words recalled is greater than the mean number of fake words recalled.

Exercise 3.
Linda made the following calculations for the two data sets:

In the previous lesson, you calculated the number of MADs that separated two sample means. You used the larger MAD to make this calculation if the two MADs were not the same. How many MADs separate the mean number of real words recalled and the mean number of fake words recalled for the students in the study?
Answer:
The difference between the two means is 9.43 – 5.36 = 4.07. The larger of the two MADs is 2.29. The number of MADs that separate the two means is \(\frac{4.07}{2.29}\), or 1.78.

Exercise 4.
In the last lesson, our work suggested that if the number of MADs that separate the two sample means is 2 or more, then it is reasonable to conclude that not only do the means differ in the samples but that the means differ in the populations as well. If the number of MADs is less than 2, then you can conclude that the difference in the sample means might just be sampling variability and that there may not be a meaningful difference in the population means. Using these criteria, what can Linda conclude about the difference in population means based on the sample data that she collected? Be sure to express your conclusion in the context of this problem.
Answer:
Since 1.78 is below the suggested 2 MADs, Linda would conclude that the average number of real words that all middle school students in her district would recall might be the same as the average number of fake words that they would recall.

Eureka Math Grade 7 Module 5 Lesson 23 Problem Set Answer Key

Question 1.
Based on Ken’s population database, compare the amount of sleep that sixth-grade females get on average to the amount of sleep that eleventh-grade females get on average.
Find the data for 15 sixth-grade females based on the following random ID numbers: 65 1 67 101 106 87 85 95 120 4 64 74 102 31 128
Find the data for 15 eleventh-grade females based on the following random ID numbers:
348 313 297 351 294 343 275 354 311 328 274 305 288 267 301
Answer:
This problem compares the amount of sleep that sixth-grade females get on average to the amount of sleep that eleventh-grade females get on average.
(Note to teachers: Random numbers are provided for students. Provide students access to the data file (a printed copy or access to the file at the website), or if that is not possible, provide them the following values to use in the remaining questions.)
Sixth-grade females’ number of hours of sleep per night: 8.2 7.8 8.0 8.1 8.7 9.0 8.9 8.7 8.4 9.0 8.4 8.5 8.8 8.5 9.2
Eleventh-grade females’ number of hours of sleep per night: 6.9 7.8 7.2 7.9 7.8 6.7 7.6 7.3 7.7 7.3 6.5 7.7 7.2 6.3 7.5

Question 2.
On the same scale, draw dot plots for the two sample data sets.
Answer:

Question 3.
Looking at the dot plots, list some observations comparing the number of hours per week that sixth graders spend on doing homework and the number of hours per week that eleventh graders spend on doing homework.
Answer:
There is a small amount of overlap between the data sets for the two random samples. The distribution of sixth-grade hours of sleep is symmetric, whereas that for eleventh graders is skewed to the left. It appears that the mean number of hours of sleep for sixth-grade females is around 8.5, and the mean number for eleventh-grade females is around 7.3 or so. Whether or not the difference is meaningful depends on the amount of variability that separates them.

Question 4.
Calculate the mean and MAD for each of the data sets. How many MADs separate the two sample means? (Use the larger MAD to make this calculation if the sample MADs are not the same.)

Answer:

The number of MADs that separate the two means is \(\frac{8.55-7.29}{0.4}\), or 3.15.

Question 5.
Recall that if the number of MADs in the difference of two sample means is greater than or equal to 2, then it would be reasonable to think that the population means are different. Using this guideline, what can you say about the average number of hours of sleep per night for all sixth-grade females in the population compared to all eleventh-grade females in the population?
Answer:
Since 3.15 is well above the criteria of 2 MADs, it can be concluded that on average sixth-grade females get more sleep per night than do eleventh-grade females.

Eureka Math Grade 7 Module 5 Lesson 23 Exit Ticket Answer Key

Question 1.
Do eleventh-grade males text more per day than eleventh-grade females do? To answer this question, two randomly selected samples were obtained from the Excel data file used in this lesson. Indicate how 20 randomly selected eleventh-grade females would be chosen for this study. Indicate how 20 randomly selected eleventh-grade males would be chosen.
Answer:
To pick 20 females, 20 randomly selected numbers from 266 to 363 would be generated from a random number generator or from a random number table. Duplicates would be disregarded, and a new number would be generated. To pick 20 males, 20 randomly selected numbers from 264 to 440 would be generated. Again, duplicates would be disregarded, and a new number would be generated.

Question 2.
Two randomly selected samples (one of eleventh-grade females and one of eleventh-grade males) were obtained from the database. The results are indicated below:

Is there a meaningful difference in the number of minutes per day that eleventh-grade females and males text? Explain your answer.
Answer:
The difference in the means is 02.55 min. – 100.32 min., or 2.23 min. (to the nearest hundredth of a minute). Divide this by 1.31 min. or the MAD for females (the larger of the two MADs): \(\frac{2.23}{1.31}\), or 1.70 to the nearest hundredth. This difference is less than 2 MADs, and therefore, the difference in the male and female number of minutes per day of texting is not a meaningful difference.

Engage NY Eureka Math 7th Grade Module 5 Lesson 22 Answer Key

Eureka Math Grade 7 Module 5 Lesson 22 Example Answer Key

Examples 1–3
Tamika’s mathematics project is to see whether boys or girls are faster in solving a KenKen-type puzzle. She creates a puzzle and records the following times that it took to solve the puzzle (in seconds) for a random sample of 10 boys from her school and a random sample of 11 girls from her school:

Example 1.
On the same scale, draw dot plots for the boys’ data and for the girls’ data. Comment on the amount of overlap between the two dot plots. How are the dot plots the same, and how are they different?
Answer:
The dot plots appear to have a considerable amount of overlap. The boys’ data may be slightly skewed to the left, whereas the girls’ are relatively symmetric.

Example 2.
Compare the variability in the two data sets using the MAD (mean absolute deviation). Is the variability in each sample about the same? Interpret the MAD in the context of the problem.
Answer:
The variability in each data set is about the same as measured by the mean absolute deviation (around 4 sec.)
For boys and girls, a typical deviation from their respective mean times (35 for boys and 39 for girls) is about 4 sec.

Example 3.
In the previous lesson, you learned that a difference between two sample means is considered to be meaningful if the difference is more than what you would expect to see just based on sampling variability. The difference in the sample means of the boys’ times and the girls’ times is 4.1 seconds (39.4 seconds – 35.3 seconds). This difference is approximately 1 MAD.
a. If4 sec. is used to approximate the value of 1 MAD for both boys and for girls, what is the interval of times that are within 1 MAD of the sample mean for boys?
Answer:
35.3 sec.+ 4 sec.=9.3 sec. , and 35.3 sec.- 4 sec.=31.4 sec. The interval of times that are within 1 MAD of the boys’ mean time is approximately 31.4 sec. to 39.3 sec.

b. Of the 10 sample means for boys, how many of them are within that interval?
Answer:
Six of the sample means for boys are within the interval.

c. Of the 11 sample means for girls, how many of them are within the interval you calculated in part (a)?
Answer:
Seven of the sample means for girls are within the interval.

d. Based on the dot plots, do you think that the difference between the two sample means is a meaningful difference? That is, are you convinced that the mean time for all girls at the school (not just this sample of girls) is different from the mean time for all boys at the school? Explain your choice based on the dot plots.
Answer:
Answers will vary. Sample answer: I don’t think that the difference is meaningful. The dot plots overlap a lot, and there is a lot of variability in the times for boys and the times for girls.

Examples 4–7
How good are you at estimating a minute? Work in pairs. Flip a coin to determine which person in the pair will go first. One of you puts your head down and raises your hand. When your partner says “Start,” keep your head down and your hand raised. When you think a minute is up, put your hand down. Your partner will record how much time has passed. Note that the room needs to be quiet. Switch roles, except this time you talk with your partner during the period when the person with his head down is indicating when he thinks a minute is up. Note that the room will not be quiet.

Answer:

Use your class data to complete the following.
Example 4.
Calculate the mean minute time for each group. Then, find the difference between the quiet mean and the talking mean.
Answer:
The mean of the quiet estimates is 58.8 sec.
The mean of the talking estimates is 64.8 sec.
64.8 – 58.8 = 6
The difference between the two means is 6 sec.

Example 5.
On the same scale, draw dot plots of the two data distributions, and discuss the similarities and differences in the two distributions.
Answer:
The dot plots have quite a bit of overlap. The quiet group distribution is fairly symmetric; the talking group distribution is skewed somewhat to the right. The variability in each is about the same. The quiet group appears to be centered around 60 sec., and the talking group appears to be centered around 65 sec.

Example 6.
Calculate the mean absolute deviation (MAD) for each data set. Based on the MADs, compare the variability in each sample. Is the variability about the same? Interpret the MADs in the context of the problem.
Answer:
The MAD for the quiet distribution is 2.68 sec.
The MAD for the talking distribution is 2.73 sec.
The MAD measurements are about the same, indicating that the variability in each data set is similar. In both groups, a typical deviation of students’ minute estimates from their respective means is about 2.7 sec.

Example 7.
Based on your calculations, is the difference in mean time estimates meaningful? Part of your reasoning should involve the number of MADs that separate the two sample means. Note that if the MADs differ, use the larger one in determining how many MADs separate the two means.
Answer:
The number of MADs that separate the two sample means is \(\frac{6}{2.73}\), or 2.2. There is a meaningful difference between the means.

Eureka Math Grade 7 Module 5 Lesson 22 Problem Set Answer Key

Question 1.
A school is trying to decide which reading program to purchase.
a. How many MADs separate the mean reading comprehension score for a standard program (mean = 67.8, MAD = 4.6, n = 24) and an activity-based program (mean = 70.3, MAD = 4.5, n = 27)?
Answer:
The number of MADs that separate the sample mean reading comprehension score for a standard program and an activity-based program is \(\frac{70.3-67.8}{4.6}\), or 0.54, about half a MAD.

b. What recommendation would you make based on this result?
Answer:
The number of MADs that separate the programs is not large enough to indicate that one program is better than the other program based on mean scores. There is no noticeable difference in the two programs.

Question 2.
Does a football filled with helium go farther than one filled with air? Two identical footballs were used: one filled with helium and one filled with air to the same pressure. Matt was chosen from the team to do the kicking. Matt did not know which ball he was kicking. The data (in yards) follow.

Answer:

a. Calculate the difference between the sample mean distance for the football filled with air and for the one filled with helium.
Answer:
The 17 air-filled balls had a mean of 27 yd. compared to 23.8 yd. for the 17 helium-filled balls, a difference of 3.2 yd.

b. On the same scale, draw dot plots of the two distributions, and discuss the variability in each distribution.
Answer:
Based on the dot plots, it looks like the variability in the two distributions is about the same.

c. Calculate the MAD for each distribution. Based on the MADs, compare the variability in each distribution. Is the variability about the same? Interpret the MADs in the context of the problem.
Answer:
The MAD is 2.59 yd. for the air-filled balls and 2.07 yd. for the helium-filled balls. The typical deviation from the mean of 27.0 is about 2.59 yd. for the air-filled balls. The typical deviation from the mean of 23.8 is about 2.07 yd. for the helium-filled balls. There is a slight difference in variability.

d. Based on your calculations, is the difference in mean distance meaningful? Part of your reasoning should involve the number of MADs that separate the sample means. Note that if the MADs differ, use the larger one in determining how many MADs separate the two means.
Answer:
\(\frac{3.2}{2.59}\) = 1.2
There is a separation of 1.2 MADs. There is no meaningful distance between the means.

Question 3.
Suppose that your classmates were debating about whether going to college is really worth it. Based on the following data of annual salaries (rounded to the nearest thousand dollars) for college graduates and high school graduates with no college experience, does it appear that going to college is indeed worth the effort? The data are from people in their second year of employment.

a. Calculate the difference between the sample mean salary for college graduates and for high school graduates.
Answer:
The 15 college graduates had a mean salary of $52,400, compared to $32,800 for the 15 high school graduates, a difference of $19,600.

b. On the same scale, draw dot plots of the two distributions, and discuss the variability in each distribution.
Answer:
Based on the dot plots, the variability of the two distributions appears to be about the same.

c. Calculate the MAD for each distribution. Based on the MADs, compare the variability in each distribution. Is the variability about the same? Interpret the MADs in the context of the problem.
Answer:
The MAD is 5.15 for college graduates and 5.17 for high school graduates. The typical deviation from the mean of 52.4 is about 5.15 (or $5,150) for college graduates. The typical deviation from the mean of 32.8 is about 5.17 ($5,170) for high school graduates. The variability in the two distributions is nearly the same.

d. Based on your calculations, is going to college worth the effort? Part of your reasoning should involve the number of MADs that separate the sample means.
Answer:
\(\frac{19.6}{5.17}\) = 3.79
There is a separation of 3.79 MADs. There is a meaningful difference between the population means. Going to college is worth the effort.

Eureka Math Grade 7 Module 5 Lesson 22 Exit Ticket Answer Key

Suppose that Brett randomly sampled 12 tenth-grade girls and boys in his school district and asked them for the number of minutes per day that they text. The data and summary measures follow.

Question 1.
Draw dot plots for the two data sets using the same numerical scales. Discuss the amount of overlap between the two dot plots that you drew and what it may mean in the context of the problem.
Answer:
There is no overlap between the two data sets. This indicates that the sample means probably differ, with girls texting more than boys on average. The girls’ data set is a little more compact than the boys, indicating that their measure of variability is smaller.

Question 2.
Compare the variability in the two data sets using the MAD. Interpret the result in the context of the problem.
Answer:
The MAD for the boys’ number of minutes spent texting is 7.9 min., which is higher than that for the girls, which is 5.3 min. This is not surprising, as seen in the dot plots. The typical deviation from the mean of 70.9 is about 7.9 min. for boys. The typical deviation from the mean of 97.3 is about 5.3 min. for girls.

Question 3.
From 1 and 2, does the difference in the two means appear to be meaningful?
Answer:
97.3 – 70.9 = 26.4
The difference in means is 26.4 min.
\(\frac{26.4}{7.9}\) = 3.3
Using the larger MAD of 7.9 min., the means are separated by 3.3 MADs. Looking at the dot plots, it certainly seems as though a separation of more than 3 MADs is meaningful.

Engage NY Eureka Math 7th Grade Module 5 Lesson 21 Answer Key

Eureka Math Grade 7 Module 5 Lesson 21 Exercise Answer Key

Exercise 1.
To begin your investigation, start by selecting a random sample of ten numbers from Bag A. Remember to mix the numbers in the bag first. Then, select one number from the bag. Do not put it back into the bag. Write the number in the chart below. Continue selecting one number at a time until you have selected ten numbers. Mix up the numbers in the bag between each selection.

Answer:

a. Create a dot plot of your sample of ten numbers. Use a dot to represent each number in the sample.
Answer:
The dot plot will vary based on the sample selected. One possible answer is shown here.

b. Do you think the mean of all the numbers in Bag A might be 10? Why or why not?
Answer:
Anticipate that students will indicate a mean of a sample from Bag A is greater than 10. Responses depend on students’ samples and the resulting dot plots. In most cases, the dots will center around a value that is greater than 10 because the mean of the population is greater than 10.

c. Based on the dot plot, what would you estimate the mean of the numbers in Bag A to be? How did you make your estimate?
Answer:
Answers will vary depending on students’ samples. Anticipate that most students’ estimates will correspond to roughly where the dots in the dot plot center. The population mean here is 14.5, so answers around 14 or 15 would be expected.

d. Do you think your sample mean will be close to the population mean? Why or why not?
Answer:
Students could answer “Yes,” “No,” or “I don’t know.” The goal of this question is to get students to think about the difference between a sample mean and the population mean.

e. Is your sample mean the same as your neighbors’ sample means? Why or why not?
Answer:
No. When selecting a sample at random, different students get different sets of numbers. This is sampling variability.

Exercise 2.
Repeat the process by selecting a random sample of ten numbers from Bag B.

Answer:

a. Create a dot plot of your sample of ten numbers. Use a dot to represent each of the numbers in the sample.
Answer:
The dot plots will vary based on the sample selected. One possible answer is shown here.

b. Based on your dot plot, do you think the mean of the numbers in Bag C is the same as or different from the mean of the numbers in Bag A? Explain your thinking.
Answer:
Answers will vary, as students will compare their center of the dot plot of the sample from Bag B to the center of the dot plot of the sample from Bag A. The centers will probably not be exactly the same; however, anticipate centers that are close to each other.

Exercise 3.
Repeat the process once more by selecting a random sample of ten numbers from Bag C.

Answer:

a. Create a dot plot of your sample of ten numbers. Use a dot to represent each of the numbers in the sample.
Answer:
The dot plots will vary based on the sample selected. One possible answer is shown here.

b. Based on your dot plot, do you think the mean of the numbers in Bag C is the same as or different from the mean of the numbers in Bag A? Explain your thinking.
Answer:
Anticipate that students will indicate that the center of the dot plot of the sample from Bag C is less than the center of the dot plot of the sample from Bag A. Because the population mean for Bag C is less than the population mean for Bag A, the center of the dot plot will usually be less for the sample from Bag C.

Exercise 4.
Are your dot plots of the three bags the same as the dot plots of other students in your class? Why or why not?
Answer:
The dot plots will vary. Because different students generally get different samples when they select a sample from the bags, the dot plots will vary from student to student.

Exercise 5.
Calculate the mean of the numbers for each of the samples from Bag A, Bag B, and Bag C.

Answer:

a. Are the sample means you calculated the same as the sample means of other members of your class? Why or why not?
Answer:
No. When selecting a sample at random, you get different sets of numbers (again, sampling variability).

b. How do your sample means for Bag A and for Bag B compare?
Answer:
Students might answer that the mean for the sample from Bag A is larger, smaller, or equal to the mean for the sample from Bag B, depending on their samples. For the example given above, the sample mean for Bag A is smaller than the sample mean for Bag B.

c. Calculate the difference of the sample mean for Bag A minus the sample mean for Bag B (Mean A – Mean B). Based on this difference, can you be sure which bag has the larger population mean? Why or why not?
Answer:
No. It is possible that you could get a sample mean that is larger than the population mean of Bag A and then get a sample mean that is smaller than the population mean of Bag B, or vice versa.

Exercise 6.
Based on the class dot plots of the sample means, do you think the mean of the numbers in Bag A and the mean of the numbers in Bag B are different? Do you think the mean of the numbers in Bag A and the mean of the numbers in Bag C are different? Explain your answers.
Answer:
Answers will vary. Sample response: Bags A and B are similar, and Bag C is different from the other two.

Exercise 7.
Based on the difference between the sample mean of Bag A and the sample mean of Bag B (Mean A – Mean B) that you calculated in Exercise 5, do you think that the two populations (Bags A and B) have different means, or do you think that the two population means might be the same?
Answer:
Answers will vary, as the difference of the means will be based on each student’s samples. Anticipate answers that indicate the difference in the sample means that the population means might be the same for differences that are close to 0. (Students learn later in this lesson that the populations of Bags A and B are the same, so most students will see differences that are not too far from 0.)

Exercise 8.
Based on this difference, can you be sure which bag has the larger population mean? Why or why not?
Answer:
No. It is possible that you could get a sample mean that is larger than the population mean of Bag A and then get a sample mean that is smaller than the population mean of Bag B, or vice versa.

Exercise 9.
Is your difference in sample means the same as your neighbors’ differences? Why or why not?
Answer:
No. As the samples will vary due to sampling variability, so will the means of each sample.

Exercise 10.
Plot your difference of the means (Mean A – Mean B) on a class dot plot. Describe the distribution of differences plotted on the graph. Remember to discuss center and spread.
Answer:
Answers will vary. The distribution of the differences is expected to cluster around 0. One example for a class of 30 students is shown here.

Exercise 11.
Why are the differences in the sample means of Bag A and Bag B not always 0?
Answer:
For the difference in sample means to be 0, the sample means must be the same value. This would rarely happen when selecting random samples.

Exercise 12.
Does the class dot plot contain differences that were relatively far away from 0? If yes, why do you think this happened?
Answer:
For the dot plot given as an example above, some differences were as large as 4.

Exercise 13.
Suppose you will take a sample from a new bag. How big would the difference in the sample mean for Bag A and the sample mean for the new bag (Mean A – Mean new) have to be before you would be convinced that the population mean for the new bag is different from the population mean of Bag A? Use the class dot plot of the differences in sample means for Bags A and B (which have equal population means) to help you answer this question.
Answer:
Students should recognize that the difference would need to be relatively far away from 0. They may give answers like “a difference of 5 (or larger)” or something similar. Remind students that the differences noted in the class dot plot are a result of sampling from bags that have the same numbers in them. As a result, students would be expected to suggest values that are greater than the values in the class dot plot.

Exercise 14.
Calculate the sample mean of Bag A minus the sample mean of Bag C (Mean A – Mean C).
Answer:
Answers will vary, as the samples collected by students will vary. Students might suspect, however, that they are being set up for a discussion about populations that have different means. As a result, ask students what they think their difference is indicating about the populations of the two bags. For several students, this difference is larger than the difference they received for Bags A and B and might suggest that the means of the bags are different.

Not all students, however, will have differences that are noticeably different from what they obtained for Bags A and B, and as a result, they will indicate that the bags could have the same or similar distribution of numbers.

Exercise 15.
Plot your difference (Mean A – Mean C) on a class dot plot.
Answer:
Have each student or group of students place their differences on a class dot plot similar to what was developed for the dot plot of the difference of means in Bags A and B. Place the dot plots next to each other so that students can compare the centers and spread of each distribution. One example based on a class of 30 students is shown here. Notice that the differences for Bag A – Bag B center around 0, while the differences for Bag A – Bag C do not center around 0.

Exercise 16.
How do the centers of the class dot plots for Mean A – Mean B and Mean A – Mean C compare?
Answer:
The center of the second dot plot Mean A – Mean C is shifted over to the right. Thus, it is not centered at 0; rather, it is centered over a value that is larger than 0.

Exercise 17.
Each bag has a population mean that is either 10.5 or 14.5. State what you think the population mean is for each bag. Explain your choice for each bag.
Answer:
The population mean is 14.5 for Bags A and B and 10.5 for Bag C. Students indicate their selections based on the class dot plots and the sample means they calculated in the exercises.

Eureka Math Grade 7 Module 5 Lesson 21 Problem Set Answer Key

Below are three dot plots. Each dot plot represents the differences in sample means for random samples selected from two populations (Bag A and Bag B). For each distribution, the differences were found by subtracting the sample means of Bag B from the sample means of Bag A (sample mean A – sample mean B).
Question 1.
Does the graph below indicate that the population mean of Bag A is larger than the population mean of Bag B? Why or why not?
Answer:
No. Since most of the differences are negative, it appears that the population mean of Bag A is smaller than the population mean of Bag B.

Question 2.
Use the graph above to estimate the difference in the population means (Mean A – Mean B).
Answer:
About -4. This is about the middle of the graph.

Question 3.
Does the graph below indicate that the population mean of Bag A is larger than the population mean of Bag B? Why or why not?
Answer:
No. The dots are all centered around 0, meaning that the population means of Bag A and Bag B might be equal.

Question 4.
Does the graph below indicate that the population mean of Bag A is larger than the population mean of Bag B? Why or why not?
Answer:
Yes. The dots are near 1.5. There is a small difference in the population means, but it is so small that it is difficult to detect. (Note to teachers: Some students may answer, “No. The dots appear centered around 0.” Problem 6 should cause students to rethink this answer.)

Question 5.
In the above graph, how many differences are greater than 0? How many differences are less than 0? What might this tell you?
Answer:
There are 18 dots greater than 0 and 12 dots less than 0. It tells me that there are more positive differences, which may mean that the population mean for Bag A is bigger than the population mean for Bag B.

Question 6.
In Problem 4, the population mean for Bag A is really larger than the population mean for Bag B. Why is it possible to still get so many negative differences in the graph?
Answer:
It is possible to get so many negative values because the population mean of Bag A may only be a little bigger than the population mean of Bag B.

Eureka Math Grade 7 Module 5 Lesson 21 Exit Ticket Answer Key

Question 1.
How is a meaningful difference in sample means different from a non-meaningful difference in sample means? You may use what you saw in the dot plots of this lesson to help you answer this question.
Answer:
A meaningful difference in sample means is one that is not likely to have occurred by just chance if there is no difference in the population means. A meaningful difference in sample means would be one that is very far from 0 (or not likely to happen if the population means are equal). A non-meaningful difference in sample means would be one that is relatively close to 0, which indicates the population means are equal.

Note that how big this difference needs to be in order to be declared meaningful depends on the context, the sample size, and the variability in the populations.

Engage NY Eureka Math 7th Grade Module 5 Lesson 20 Answer Key

Eureka Math Grade 7 Module 5 Lesson 20 Example Answer Key

Example 2: Estimating Population Proportion
Two hundred middle school students at Roosevelt Middle School responded to several survey questions. A printed copy of the responses the students gave to various questions will be provided by your teacher.
The data are organized in columns and are summarized by the following table:

The last column in the data file is based on the question: Which of the following superpowers would you most like to have? The choices were invisibility, super strength, telepathy, fly, or freeze time.

The class wants to determine the proportion of Roosevelt Middle School students who answered “freeze time” to the last question. You will use a sample of the Roosevelt Middle School population to estimate the proportion of the students who answered “freeze time” to the last question.
A random sample of 20 student responses is needed. You are provided the random number table you used in a previous lesson. A printed list of the 200 Roosevelt Middle School students is also provided. In small groups, complete the following exercise:
a. Select a random sample of 20 student responses from the data file. Explain how you selected the random sample.
Answer:
Generate 20 random numbers between 1 and 200. The random number chosen represents the ID number of the student. Go to that ID number row, and record the outcome as “yes” or “no” in the table regarding the freeze time response.

b. In the table below, list the 20 responses for your sample.

Answer:
Answers will vary. Below is one possible result.

c. Estimate the population proportion of students who responded “freeze time” by calculating the sample proportion of the 20 sampled students who responded “freeze time” to the question.
Answer:
Students’ answers will vary. The sample proportion in the given example is \(\frac{5}{20}\), or 0.25.

d. Combine your sample proportion with other students’ sample proportions, and create a dot plot of the distribution of the sample proportions of students who responded “freeze time” to the question.
Answer:
An example is shown below. The class dot plot may differ somewhat from the one below, but the distribution should center at approximately 0.20. (Provide students this distribution of sample proportions if they were unable to obtain a distribution.)

e. By looking at the dot plot, what is the value of the proportion of the 200 Roosevelt Middle School students who responded “freeze time” to the question?
Answer:
0.20

f. Usually, you will estimate the proportion of Roosevelt Middle School students using just a single sample proportion. How different was your sample proportion from your estimate based on the dot plot of many samples?
Answer:
Students’ answers will vary depending on their sample proportions. For this example, the sample proportion is 0.25, which is slightly greater than the 0.20.

g. Circle your sample proportion on the dot plot. How does your sample proportion compare with the mean of all the sample proportions?
Answer:
The mean of the class distribution will vary from this example. The class distribution should center at approximately 0.20.

h. Calculate the mean of all of the sample proportions. Locate the mean of the sample proportions in your dot plot; mark this position with an X. How does the mean of the sample proportions compare with your sample proportion?
Answer:
Answers will vary based on the samples generated by students.

Eureka Math Grade 7 Module 5 Lesson 20 Exercise Answer Key

Exercises 1–9

Exercise 1.
The first student reported a sample proportion of 0.15. Interpret this value in terms of the summary of the problem in the example.
Answer:
Three of the 20 students surveyed responded that they were vegetarian.

Exercise 2.
Another student reported a sample proportion of 0. Did this student do something wrong when selecting the sample of middle school students?
Answer:
No. This means that none of the 20 students surveyed said that they were vegetarian.

Exercise 3.
Assume you were part of this seventh-grade class and you got a sample proportion of 0.20 from a random sample of middle school students. Based on this sample proportion, what is your estimate for the proportion of all middle school students who are vegetarians?
Answer:
My estimate is 0.20.

Exercise 4.
Construct a dot plot of the 30 sample proportions.
Answer:

Exercise 5.
Describe the shape of the distribution.
Answer:
Nearly symmetrical or mound shaped centering at approximately 0.15

Exercise 6.
Using the 30 class results listed above, what is your estimate for the proportion of all middle school students who are vegetarians? Explain how you made this estimate.
Answer:
About 0.15. I chose this value because the sample proportions tend to cluster between 0.10 and 0.15 or 0.10 and 0.20.

Exercise 7.
Calculate the mean of the 30 sample proportions. How close is this value to the estimate you made in Exercise 6?
Answer:
The mean of the 30 samples to the nearest thousandth is 0.153. The value is close to my estimate of 0.15, and if calculated to the nearest hundredth, they would be the same. (Most likely, students will say between 0.10 and 0.15.)

Exercise 8.
The proportion of all middle school students who are vegetarians is 0.15. This is the actual proportion for the entire population of middle school students used to select the samples. How the mean of the 30 sample proportions compares with the actual population proportion depends on the students’ samples.
Answer:
In this case, the mean of the 30 sample proportions is very close to the actual population proportion.

Exercise 9.
Do the sample proportions in the dot plot tend to cluster around the value of the population proportion? Are any of the sample proportions far away from 0.15? List the proportions that are far away from 0.15.
Answer:
They cluster around 0.15. The values of 0 and 0.30 are far away from 0.15.

Eureka Math Grade 7 Module 5 Lesson 20 Problem Set Answer Key

Question 1.
A class of 30 seventh graders wanted to estimate the proportion of middle school students who played a musical instrument. Each seventh grader took a random sample of 25 middle school students and asked each student whether or not he or she played a musical instrument. The following are the sample proportions the seventh graders found in 30 samples.

a. The first student reported a sample proportion of 0.80. What does this value mean in terms of this scenario?
Answer:
A sample proportion of 0.80 means 20 out of 25 answered yes to the survey.

b. Construct a dot plot of the 30 sample proportions.
Answer:

c. Describe the shape of the distribution.
Answer:
Nearly symmetrical. It centers at approximately 0.72.

d. Describe the variability of the distribution.
Answer:
The spread of the distribution is from 0.60 to 0.84.

e. Using the 30 class sample proportions listed on the previous page, what is your estimate for the proportion of all middle school students who played a musical instrument?
Answer:
The mean of the 30 sample proportions is approximately 0.713.

Question 2.
Select another variable or column from the data file that is of interest. Take a random sample of 30 students from the list, and record the response to your variable of interest of each of the 30 students.
a. Based on your random sample, what is your estimate for the proportion of all middle school students?
Answer:
Students’ answers will vary depending on the column chosen.

b. If you selected a second random sample of 30, would you get the same sample proportion for the second random sample that you got for the first random sample? Explain why or why not.
Answer:
No. It is very unlikely that you would get exactly the same result. This is sampling variability—the value of a sample statistic will vary from one sample to another.

Eureka Math Grade 7 Module 5 Lesson 20 Exit Ticket Answer Key

Thirty seventh graders each took a random sample of 10 middle school students and asked each student whether or not he likes pop music. Then, they calculated the proportion of students who like pop music for each sample. The dot plot below shows the distribution of the sample proportions.

Question 1.
There are three dots above 0.2. What does each dot represent in terms of this scenario?
Answer:
Each dot represents the survey results from one student. 0.2 means two students out of 10 said they like pop music.

Question 2.
Based on the dot plot, do you think the proportion of the middle school students at this school who like pop music is 0.6? Explain why or why not.
Answer:
No. Based on the dot plot, 0.6 is not a likely proportion. The dots cluster at 0.3 to 0.5, and only a few dots were located at 0.6. An estimate of the proportion of students at this school who like pop music would be within the cluster of 0.3 to 0.5.

Engage NY Eureka Math 7th Grade Module 5 Lesson 19 Answer Key

Eureka Math Grade 7 Module 5 Lesson 19 Example Answer Key

Example 1: Sample Proportion
Your teacher will give your group a bag that contains colored cubes, some of which are red. With your classmates, you are going to build a distribution of sample proportions.
a. Each person in your group should randomly select a sample of 10 cubes from the bag. Record the data for your sample in the table below.

Answer:
Students’ tables will vary based on their samples.

b. What is the proportion of red cubes in your sample of 10?
This value is called the sample proportion. The sample proportion is found by dividing the number of successes (in this example, the number of red cubes) by the total number of observations in the sample.
Answer:
Students’ results will be around 0.4. In this example, the sample proportion is 0.3.

c. Write your sample proportion on a sticky note, and place it on the number line that your teacher has drawn on the board. Place your note above the value on the number line that corresponds to your sample proportion.
The graph of all students’ sample proportions is called a sampling distribution of the sample proportions.
Answer:
This is an example of a dot plot of the sampling distribution.

d. Describe the shape of the distribution.
Answer:
A nearly symmetrical distribution that is clustered around 0.4

e. Describe the variability in the sample proportions.
Answer:
The spread of the data is from 0.1 to 0.7. Much of the data cluster between 0.3 and 0.5.

Based on the distribution, answer the following:
f. What do you think is the population proportion?
Answer:
Based on the dot plot, an estimate of the population proportion is approximately 0.4.

g. How confident are you of your estimate?
Answer:
Because there is a lot of variability from sample to sample (0.1 to 0.7), I do not have a lot of confidence in my estimate.

Example 2: Sampling Variability
What do you think would happen to the sampling distribution if everyone in class took a random sample of 30 cubes from the bag? To help answer this question, you will repeat the random sampling you did in part (a) of Example 1, except now you will draw a random sample of 30 cubes instead of 10.
a. Take a random sample of 30 cubes from the bag. Carefully record the outcome of each draw.

Answer:
Answers will vary. An example follows:

b. What is the proportion of red cubes in your sample of 30?
Answer:
Answers will vary. In this example, the sample proportion is \(\frac{11}{30}\), or approximately 0.367.

c. Write your sample proportion on a sticky note, and place the note on the number line that your teacher has drawn on the board. Place your note above the value on the number line that corresponds to your sample proportion.
Answer:
An example of a dot plot:

d. Describe the shape of the distribution.
Answer:
Mound shaped, centered around 0.4

Eureka Math Grade 7 Module 5 Lesson 19 Exercise Answer Key

Exercises 1–5

Exercise 1.
Describe the variability in the sample proportions.
Answer:
The spread of the data is from 0.25 to 0.55. Most of the data cluster between 0.35 and 0.5.

Exercise 2.
Based on the distribution, answer the following:
a. What do you think is the population proportion?
Answer:
Based on the dot plot, an estimate of the population proportion is approximately 0.4.

b. How confident are you of your estimate?
Answer:
Because there is less variability from sample to sample (0.35 to 0.5), I am more confident in my estimate.

c. If you were taking a random sample of 30 cubes and determined the proportion that was red, do you think your sample proportion will be within 0.05 of the population proportion? Explain.
Answer:
Answers depend on the dot plots prepared by students. If the dot plot in Example 2 part (c), is used as an example, note that only about half of the dots are between 0.35 and 0.45. There are several samples that had sample proportions that were farther away from the center than 0.05, so the sample proportion might not be within 0.05 of the population proportion.

Exercise 3.
Compare the sampling distribution based on samples of size 10 to the sampling distribution based on samples of size 30.
Answer:
Both distributions are mound shaped and center around 0.4. Variability is less in the sampling distribution of sample sizes of 30 versus sample sizes of 10.

Exercise 4.
As the sample size increased from 10 to 30, describe what happened to the sampling variability of the sample proportions.
Answer:
The sampling variability decreased as the sample size increased.

Exercise 5.
What do you think would happen to the sampling variability of the sample proportions if the sample size for each sample was 50 instead of 30? Explain.
Answer:
The sampling variability in the sampling distribution for samples of size 50 will be less than the sampling variability of the sampling distribution for samples of size 30.

Eureka Math Grade 7 Module 5 Lesson 19 Problem Set Answer Key

Question 1.
A class of seventh graders wanted to find the proportion of M&M’s^® that are red. Each seventh grader took a random sample of 20 M&M’s^® from a very large container of M&M’s^®. The following is the proportion of red M&M’s each student found.

a. Construct a dot plot of the sample proportions.
Answer:

b. Describe the shape of the distribution.
Answer:
Somewhat mound shaped, slightly skewed to the right

c. Describe the variability of the distribution.
Answer:
The spread of the data is from 0.0 to 0.3. Most of the data cluster between 0.10 and 0.20.

d. Suppose the seventh-grade students had taken random samples of size 50. Describe how the sampling distribution would change from the one you constructed in part (a).
Answer:
The sampling variability would decrease.

Question 2.
A group of seventh graders wanted to estimate the proportion of middle school students who suffer from allergies. The members of one group of seventh graders each took a random sample of 10 middle school students, and the members of another group of seventh graders each took a random sample of 40 middle school students. Below are two sampling distributions of the sample proportions of middle school students who said that they suffer from allergies. Which dot plot is based on random samples of size 40? How can you tell?


Answer:
Dot Plot A is based on random samples of size 40 rather than random samples of size 10 because the variability of the distribution is less than the variability in Dot Plot B.

Question 3.
The nurse in your school district would like to study the proportion of middle school students who usually get at least eight hours of sleep on school nights. Suppose each student in your class plans on taking a random sample of 20 middle school students from your district, and each calculates a sample proportion of students who said that they usually get at least eight hours of sleep on school nights.

a. Do you expect everyone in your class to get the same value for their sample proportions? Explain.
Answer:
No. We expect sample variability.

b. Suppose each student in class increased the sample size from 20 to 40. Describe how you could reduce the sampling variability.
Answer:
I could reduce the sampling variability by using the larger sample size.

Eureka Math Grade 7 Module 5 Lesson 19 Exit Ticket Answer Key

A group of seventh graders took repeated samples of size 20 from a bag of colored cubes. The dot plot below shows the sampling distribution of the sample proportion of blue cubes in the bag.

Question 1.
Describe the shape of the distribution.
Answer:
Mound shaped, centered around 0.55

Question 2.
Describe the variability of the distribution.
Answer:
The spread of the data is from 0.35 to 0.75, with much of the data between 0.50 and 0.65.

Question 3.
Predict how the dot plot would look differently if the sample sizes had been 40 instead of 20.
Answer:
The variability will decrease as the sample size increases. The dot plot will be centered in a similar place but will be less spread out.

Engage NY Eureka Math 7th Grade Module 5 Lesson 18 Answer Key

Eureka Math Grade 7 Module 5 Lesson 18 Example Answer Key

Example 1: Sampling Variability
The previous lesson investigated the statistical question “What is the typical time spent at the gym?” by selecting random samples from the population of 800 gym members. Two different dot plots of sample means calculated from random samples from the population are displayed below. The first dot plot represents the means of 20 samples with each sample having 5 data points. The second dot plot represents the means of 20 samples with each sample having 15 data points.

Based on the first dot plot, Jill answered the statistical question by indicating the mean time people spent at the gym was between 34 and 78 minutes. She decided that a time approximately in the middle of that interval would be her estimate of the mean time the 800 people spent at the gym. She estimated 52 minutes. Scott answered the question using the second dot plot. He indicated that the mean time people spent at the gym was between 41 and 65 minutes. He also selected a time of 52 minutes to answer the question.

a. Describe the differences in the two dot plots.
Answer:
The first dot plot shows a greater variability in the sample means than the second dot plot.

b. Which dot plot do you feel more confident in using to answer the statistical question? Explain your answer.
Answer:
Possible response: The second dot plot gives me more confidence because the sample means do not differ as much from one another. They are more tightly clustered, so I think I have a better idea of where the population mean is located.

c. In general, do you want sampling variability to be large or small? Explain.
Answer:
The larger the sampling variability, the more that the value of a sample statistic varies from one sample to another and the farther you can expect a sample statistic value to be from the population characteristic. You want the value of the sample statistic to be close to the population characteristic. So, you want sampling variability to be small.

Eureka Math Grade 7 Module 5 Lesson 18 Exercise Answer Key

Exercises 1–3
In the previous lesson, you saw a population of 800 times spent at the gym. You will now select a random sample of size 15 from that population. You will then calculate the sample mean.

Exercise 1.
Start by selecting a three-digit number from the table of random digits. Place the random digit table in front of you. Without looking at the page, place the eraser end of your pencil somewhere on the table of random digits. Start using the table of random digits at the digit closest to your eraser. This digit and the following two specify which observation from the population will be the first observation in your sample. Write the value of this observation in the space below. (Discard any three-digit number that is 800 or larger, and use the next three digits from the random digit table.)
Answer:
Answers will vary.

Exercise 2.
Continue moving to the right in the table of random digits from the point that you reached in Exercise 1. Each three-digit number specifies a value to be selected from the population. Continue in this way until you have selected 14 more values from the population. This will make 15 values altogether. Write the values of all 15 observations in the space below.
Answer:
Answers will vary.

Exercise 3.
Calculate the mean of your 15 sample values. Write the value of your sample mean below. Round your answer to the nearest tenth. (Be sure to show your work.)
Answer:
Answers will vary.

Exercises 4–6
You will now use the sample means from Exercise 3 for the entire class to make a dot plot.

Exercise 4.
Write the sample means for everyone in the class in the space below.
Answer:
Answers will vary.

Exercise 5.
Use all the sample means to make a dot plot using the axis given below. (Remember, if you have repeated values or values close to each other, stack the dots one above the other.)

Answer:
Answers will vary.

Exercise 6.
In the previous lesson, you drew a dot plot of sample means for samples of size 5. How does the dot plot above
(of sample means for samples of size 15) compare to the dot plot of sample means for samples of size 5? For which sample size (5 or 15) does the sample mean have the greater sampling variability?

This exercise illustrates the notion that the greater the sample size, the smaller the sampling variability of the sample mean.
Answer:
The dot plots will vary depending on the results of the random sampling. Dot plots for one set of sample means for 20 random samples of size 5 and for 20 random samples of size 15 are shown below. The main thing for students to notice is that there is less variability from sample to sample for the larger sample size.

This exercise illustrates the notion that the greater the sample size, the smaller the sampling variability of the sample mean.

Exercises 7–8

Exercise 7.
Remember that in practice you only take one sample. Suppose that a statistician plans to take a random sample of size 15 from the population of times spent at the gym and will use the sample mean as an estimate of the population mean. Based on the dot plot of sample means that your class collected from the population, approximately how far can the statistician expect the sample mean to be from the population mean? (The actual population mean is 53.9 minutes.)
Answer:
Answers will vary according to the degree of variability that appears in the dot plot and a student’s estimate of an average distance from the population mean. Allow students to use an approximation of 54 minutes for the population mean. In the example above, the 20 samples could be used to estimate the mean distance of the sample means to the population mean of 54 minutes.

The sum of the distances from the mean in the above example is 137. The mean of these distances, or the expected distance of a sample mean from the population mean, is 6.85 minutes.

Exercise 8.
How would your answer in Exercise 7 compare to the equivalent mean of the distances for a sample of size 5?
Answer:
Sample response: My answer for Exercise 7 is smaller than the expected distance for the samples of size 5. For samples of size 5, several dots are farther from the mean of 54 minutes. The mean of the distance for samples of size 5 would be larger.

Exercises 9–11
Suppose everyone in your class selected a random sample of size 25 from the population of times spent at the gym.

Exercise 9.
What do you think the dot plot of the class’s sample means would look like? Make a sketch using the axis below.

Answer:
Students’ sketches should show dots that have less spread than those in the dot plot for samples of size 15.
For example, students’ dot plots might look like this:

Exercise 10.
Suppose that a statistician plans to estimate the population mean using a sample of size 25. According to your sketch, approximately how far can the statistician expect the sample mean to be from the population mean?
Answer:
We were told in Exercise 7 that the population mean is 53.9. If you calculate the mean of the distances from the population mean (in the same way you did in Exercise 7), the average or expected distance of a sample mean from 53.9 is approximately 3 minutes for a dot plot similar to the one above. This estimate is made by approximating the average distance of each dot from 53.9 or 54. Note: If necessary, make a chart similar to what was suggested in Exercise 7. Using the dot plot, direct students to estimate the distance of each dot from 54 (rounding to the nearest whole number is adequate for this question), add up the distances, and divide by the number of dots.

Exercise 11.
Suppose you have a choice of using a sample of size 5, 15, or 25. Which of the three makes the sampling variability of the sample mean the smallest? Why would you choose the sample size that makes the sampling variability of the sample mean as small as possible?
Answer:
Choosing a sample size of 25 makes the sampling variability of the sample mean the smallest, which is preferable because the sample mean is then more likely to be closer to the population mean than it would be for the smaller sample sizes.

Eureka Math Grade 7 Module 5 Lesson 18 Problem Set Answer Key

Question 1.
The owner of a new coffee shop is keeping track of how much each customer spends (in dollars). One hundred of these amounts are shown in the table below. These amounts will form the population for this question.

a. Place the table of random digits in front of you. Select a starting point without looking at the page. Then, taking two digits at a time, select a random sample of size 10 from the population above. Write the 10 values in the space below. (For example, suppose you start at the third digit of row four of the random digit table. Taking two digits gives you 19. In the population above, go to the row labeled 1, and move across to the column labeled 9. This observation is 4.98, and that will be the first observation in your sample. Then, continue in the random digit table from the point you reached.)
Answer:
a. For example (starting in the random digit table at the 8 th digit in row 15):
5.12, 5.47, 5.71, 6.18, 4.55, 5.12, 3.63, 5.12, 5.71, 4.34.
Calculate the mean for your sample, showing your work. Round your answer to the nearest thousandth.
\(\frac{5.12+5.47+5.71+6.18+4.55+5.12+3.63+5.12+5.71+4.34}{10}\) = 5.095
Calculate the mean for your sample, showing your work. Round your answer to the nearest thousandth.
Answer:
For example (starting in the random digit table at the 8 th digit in row 15):
5.12, 5.47, 5.71, 6.18, 4.55, 5.12, 3.63, 5.12, 5.71, 4.34.
Calculate the mean for your sample, showing your work. Round your answer to the nearest thousandth.
\(\frac{5.12+5.47+5.71+6.18+4.55+5.12+3.63+5.12+5.71+4.34}{10}\) = 5.095

b. Using the same approach as in part (a), select a random sample of size 20 from the population.
Calculate the mean for your sample of size 20. Round your answer to the nearest thousandth.
Answer:
For example (continuing in the random digit table from the point reached in part (a)):
6.39, 5.58, 4.67, 5.12, 3.90, 3.92, 5.57, 6.34, 5.25, 6.18, 5.71, 6.18, 7.43, 4.06, 4.19, 7.43, 4.34, 4.06, 5.42, 5.42.
Calculate the mean for your sample of size 20. Round your answer to the nearest thousandth.
\(\frac{6.39+\cdots+5.42}{20}\) = 5.358

c. Which of your sample means is likely to be the better estimate of the population mean? Explain your answer in terms of sampling variability.
Answer:
The sample mean from the sample of size 20 is likely to be the better estimate since larger samples result in smaller sampling variability of the sample mean.

Question 2.
Two dot plots are shown below. One of the dot plots shows the values of some sample means from random samples of size 10 from the population given in Problem 1. The other dot plot shows the values of some sample means from random samples of size 20 from the population given in Problem 1.

Which dot plot is for sample means from samples of size 10, and which dot plot is for sample means from samples of size 20? Explain your reasoning.
The sample means from samples of size 10 are shown in Dot Plot __________.
The sample means from samples of size 20 are shown in Dot Plot ___________.
Answer:
The sample means from samples of size 10 are shown in Dot Plot A.
The sampling variability is greater than in Dot Plot B.

The sample means from samples of size 20 are shown in Dot Plot B.
The sampling variability is smaller compared to Dot Plot A, which implies that the sample size was greater.

Question 3.
You are going to use a random sample to estimate the mean travel time for getting to school for all the students in your grade. You will select a random sample of students from your grade. Explain why you would like the sampling variability of the sample mean to be small.
Answer:
I would like the sampling variability of the sample mean to be small because then it is likely that my sample mean will be close to the mean time for all students at the school.

Eureka Math Grade 7 Module 5 Lesson 18 Exit Ticket Answer Key

Suppose that you wanted to estimate the mean time per evening spent doing homework for students at your school. You decide to do this by taking a random sample of students from your school. You will calculate the mean time spent doing homework for your sample. You will then use your sample mean as an estimate of the population mean.
Question 1.
The sample mean has sampling variability. Explain what this means.
Answer:
There are many different possible samples of students at my school, and the value of the sample mean varies from sample to sample.

Question 2.
When you are using a sample statistic to estimate a population characteristic, do you want the sampling variability of the sample statistic to be large or small? Explain why.
Answer:
You want the sampling variability of the sample statistic to be small because then you can expect the value of your sample statistic to be close to the value of the population characteristic that you are estimating.

Question 3.
Think about your estimate of the mean time spent doing homework for students at your school. Given a choice of using a sample of size 20 or a sample of size 40, which should you choose? Explain your answer.
Answer:
I would use a sample of size 40 because then the sampling variability of the sample mean would be smaller than it would be for a sample of size 20.

Engage NY Eureka Math 7th Grade Module 5 Lesson 17 Answer Key

Eureka Math Grade 7 Module 5 Lesson 17 Exercise Answer Key

Exercises 1–4
Initially, you will select just five values from the population to form your sample. This is a very small sample size, but it is a good place to start to understand the ideas of this lesson.

Exercise 1.
Use the table of random numbers to select five values from the population of times. What are the five observations in your sample?
Answer:
Make sure students write down these values and understand how they were selected. In the example given, the following observations were selected: 53 min., 63 min., 31 min., 70 min., and 42 min.

Exercise 2.
For the sample that you selected, calculate the sample mean.
Answer:
\(\frac{53+63+31+70+42}{5}\) = 51.8
For the given example, the sample mean is 51.8 min.

Exercise 3.
You selected a random sample and calculated the sample mean in order to estimate the population mean. Do you think that the mean of these five observations is exactly correct for the population mean? Could the population mean be greater than the number you calculated? Could the population mean be less than the number you calculated?
Answer:
Make sure that students see that the value of their sample mean (51.8 minutes in the given example, but students will have different sample means) is not likely to be exactly correct for the population mean. The population mean could be greater or less than the value of the sample mean.

Exercise 4.
In practice, you only take one sample in order to estimate a population characteristic. But, for the purposes of this lesson, suppose you were to take another random sample from the same population of times at the gym. Could the new sample mean be closer to the population mean than the mean of these five observations? Could it be farther from the population mean?
Answer:
Make sure students understand that if they were to take a new random sample, the new sample mean is unlikely to be equal to the value of the sample mean of their first sample. It could be closer to or farther from the population mean.

Exercises 5–7
As a class, you will now investigate sampling variability by taking several samples from the same population. Each sample will have a different sample mean. This variation provides an example of sampling variability.

Exercise 5.
Place the table of random digits in front of you, and without looking at the page, place the eraser end of your pencil somewhere on the table of random numbers. Start using the table of random digits at the number closest to where your eraser touches the paper. This digit and the following two specify which observation from the population tables will be the first observation in your sample. Write this three-digit number and the corresponding data value from the population in the space below.
Answer:
Answers will vary based on the numbers selected.

Exercise 6.
Continue moving to the right in the table of random digits from the place you ended in Exercise 5. Use three digits at a time. Each set of three digits specifies which observation in the population is the next number in your sample. Continue until you have four more observations, and write these four values in the space below.
Answer:
Answers will vary based on the numbers selected.

Exercise 7.
Calculate the mean of the five values that form your sample. Round your answer to the nearest tenth. Show your work and your sample mean in the space below.
Answer:
Answers will vary based on the numbers selected.

Exercises 8–11
You will now use the sample means from Exercise 7 from the entire class to make a dot plot.

Exercise 8.
Write the sample means for everyone in the class in the space below.
Answer:
Answers will vary based on the collected sample means.

Exercise 9.
Use all the sample means to make a dot plot using the axis given below. (Remember, if you have repeated or close values, stack the dots one above the other.)

Answer:

Exercise 10.
What do you see in the dot plot that demonstrates sampling variability?
Answer:
Sample response: The dots are spread out, indicating that the sample means are not the same. The results indicate what we discussed as sampling variability. (See the explanation provided at the end of this lesson.)

Exercise 11.
Remember that in practice you only take one sample. (In this lesson, many samples were taken in order to demonstrate the concept of sampling variability.) Suppose that a statistician plans to take a random sample of size 5 from the population of times spent at the gym and that he will use the sample mean as an estimate of the population mean. Approximately how far can the statistician expect the sample mean to be from the population mean?
Population


Population (continued)


Table of Random Digits

Answer:
Answers will vary. Allow students to speculate as to what the value of the population mean might be and how far a sample mean would be from that value. The distance students indicate are based on the dot plot. Students may indicate the sample mean to be exactly equal to the population and that the distance would be 0.

They may also indicate the sample mean to be one of the dots that is a minimum or a maximum of the distribution and suggest a distance from the minimum or maximum to the center of the distribution. Students should begin to see that the distribution has a center that they suspect is close to the population’s mean.

Eureka Math Grade 7 Module 5 Lesson 17 Problem Set Answer Key

Question 1.
Youself intends to buy a car. He wishes to estimate the mean fuel efficiency (in miles per gallon) of all cars available at this time. Yousef selects a random sample of 10 cars and looks up their fuel efficiencies on the Internet.
The results are shown below.
22 25 29 23 31 29 28 22 23 27
a. Yousef will estimate the mean fuel efficiency of all cars by calculating the mean for his sample. Calculate the sample mean, and record your answer. (Be sure to show your work.)
Answer:
\(\frac{22+25+29+23+31+29+28+22+23+27}{10}\) = 25.9

b. In practice, you only take one sample to estimate a population characteristic. However, if Yousef were to take another random sample of 10 cars from the same population, would he likely get the same value for the sample mean?
Answer:
No. It is not likely that Yousef would get the same value for the sample mean.

c. What if Yousef were to take many random samples of 10 cars? Would all of the sample means be the same?
Answer:
No. He could get many different values of the sample mean.

d. Using this example, explain what sampling variability means.
Answer:
The fact that the sample mean varies from sample to sample is an example of sampling variability.

Question 2.
Think about the mean number of siblings (brothers and sisters) for all students at your school.
a. What do you think is the approximate value of the mean number of siblings for the population of all students at your school?
Answer:
Answers will vary.

b. How could you find a better estimate of this population mean?
Answer:
I could take a random sample of students, ask the students in my sample how many siblings they have, and find the mean for my sample.

c. Suppose that you have now selected a random sample of students from your school. You have asked all of the students in your sample how many siblings they have. How will you calculate the sample mean?
Answer:
I will add up all of the values in the sample and divide by the number of students in the sample.

d. If you had taken a different sample, would the sample mean have taken the same value?
Answer:
No. A different sample would generally produce a different value of the sample mean. It is possible but unlikely that the sample mean for a different sample would have the same mean.

e. There are many different samples of students that you could have selected. These samples produce many different possible sample means. What is the phrase used for this concept?
Answer:
Sampling variability

f. Does the phrase you gave in part (e) apply only to sample means?
Answer:
No. The concept of sampling variability applies to any sample statistic.

Eureka Math Grade 7 Module 5 Lesson 17 Exit Ticket Answer Key

Suppose that you want to estimate the mean time per evening students at your school spend doing homework. You will do this using a random sample of 30 students.
Question 1.
Suppose that you have a list of all the students at your school. The students are numbered 1,2,3,…. One way to select the random sample of students is to use the random digit table from today’s class, taking three digits at a time. If you start at the third digit of Row 9, what is the number of the first student you would include in your sample?
Answer:
The first student in the sample would be student number 229.

Question 2.
Suppose that you have now selected your random sample and that you have asked the students how long they spend doing homework each evening. How will you use these results to estimate the mean time spent doing homework for all students?
Answer:
I would calculate the mean time spent doing homework for the students in my sample.

Question 3.
Explain what is meant by sampling variability in this context.
Answer:
Different samples of students would result in different values of the sample mean. This is sampling variability of the sample mean.

Engage NY Eureka Math 7th Grade Module 5 Lesson 9 Answer Key

Eureka Math Grade 7 Module 5 Lesson 9 Exploratory Challenge Answer Key

Exploratory Challenge: Game Show—Picking Blue!
Imagine, for a moment, the following situation: You and your classmates are contestants on a quiz show called Picking Blue! There are two bags in front of you, Bag A and Bag B. Each bag contains red and blue chips. You are told that one of the bags has exactly the same number of blue chips as red chips. But you are told nothing about the ratio of blue to red chips in the other bag.

Each student in your class will be asked to select either Bag A or Bag B. Starting with Bag A, a chip is randomly selected from the bag. If a blue chip is drawn, all of the students in your class who selected Bag A win a blue token. The chip is put back in the bag. After mixing up the chips in the bag, another chip is randomly selected from the bag. If the chip is blue, the students who picked Bag A win another blue token. After the chip is placed back into the bag, the process continues until a red chip is picked. When a red chip is picked, the game moves to Bag B. A chip from Bag B is then randomly selected. If it is blue, all of the students who selected Bag B win a blue token. But if the chip is red, the game is over. Just like for Bag A, if the chip is blue, the process repeats until a red chip is picked from the bag. When the game is over, the students with the greatest number of blue tokens are considered the winning team.

Without any information about the bags, you would probably select a bag simply by guessing. But surprisingly, the show’s producers are going to allow you to do some research before you select a bag. For the next 20 minutes, you can pull a chip from either one of the two bags, look at the chip, and then put the chip back in the bag. You can repeat this process as many times as you want within the 20 minutes. At the end of 20 minutes, you must make your final decision and select which of the bags you want to use in the game.

Getting Started
Assume that the producers of the show do not want to give away a lot of their blue tokens. As a result, if one bag has the same number of red and blue chips, do you think the other bag would have more or fewer blue chips than red chips? Explain your answer.
Answer:
The producers would likely want the second bag to have fewer blue chips. If a participant selects that bag, it would mean the participant is more likely to lose this game.

Eureka Math Grade 7 Module 5 Lesson 9 Examining Your Results Answer Key

At the end of the game, your teacher will open the bags and reveal how many blue and red chips were in each bag. Answer the questions that follow. After you have answered these questions, discuss them with your class.
Question 1.
Before you played the game, what were you trying to learn about the bags from your research?
Answer:
I was trying to learn the estimated probability of picking a blue chip without knowing the theoretical probability.

Question 2.
What did you expect to happen when you pulled chips from the bag with the same number of blue and red chips? Did the bag that you thought had the same number of blue and red chips yield the results you expected?
Answer:
I was looking for an estimated probability that was close to 0.5. That would connect the estimated probability of picking blue with the bag that had the same number of red and blue chips.

Question 3.
How confident were you in predicting which bag had the same number of blue and red chips? Explain.
Answer:
Answers will vary. Students’ confidence is based on the data collected. The more data collected, the closer the estimates are likely to be to the actual probabilities.

Question 4.
What bag did you select to use in the competition, and why?
Answer:
Answers will vary. It is anticipated that students would pick the bag with the larger estimated probability of picking a blue chip based on the many chips they selected during the research stage. Evidence of choices might include I picked 50 chips from Bag A, and 24 were blue, and 26 were red. The results are very close to 0.5 probability of picking each color. I think this indicates that there were likely an equal number of each color in this bag.

Question 5.
If you were the show’s producers, how would you make up the second bag? (Remember, one bag has the same number of red and blue chips.)
Answer:
Answers will vary. Most students should indicate a second bag that had fewer blue chips, but some may speculate on a second bag that is nearly the same (to make the game more of a guessing game) or a bag with very few blue (thus providing a clearer indication which bag had the same number of red and blue chips).

Question 6.
If you picked a chip from Bag B 100 times and found that you picked each color exactly 50 times, would you know for sure that Bag B was the one with equal numbers of each color?
Answer:
Student answers should indicate that they are quite confident they have the right bag, as getting that result is likely to occur from the bag with equal numbers of each colored chip. However, answers should represent understanding that even a bag with a different number of colored chips could have that outcome.

Eureka Math Grade 7 Module 5 Lesson 9 Problem Set Answer Key

Jerry and Michael played a game similar to Picking Blue! The following results are from their research using the same two bags:

Question 1.
If all you knew about the bags were the results of Jerry’s research, which bag would you select for the game? Explain your answer.
Answer:
Using only Jerry’s research, I would select Bag A because the greater relative frequency of picking a blue chip would be Bag A, or 0.8. There were 10 selections. Eight of the selections resulted in picking blue.

Question 2.
If all you knew about the bags were the results of Michael’s research, which bag would you select for the game? Explain your answer.
Answer:
Using Michael’s research, I would select Bag B because the greater relative frequency of picking a blue chip would be Bag B, or \(\frac{18}{40}\) = 0.45. There were 40 selections. Eighteen of the selections resulted in picking blue.

Question 3.
Does Jerry’s research or Michael’s research give you a better indication of the makeup of the blue and red chips in each bag? Explain why you selected this research.
Answer:
Michael’s research would provide a better indication of the probability of picking a blue chip, as it was carried out 40 times compared to 10 times for Jerry’s research. The more outcomes that are carried out, the closer the relative frequencies approach the theoretical probability of picking a blue chip.

Question 4.
Assume there are 12 chips in each bag. Use either Jerry’s or Michael’s research to estimate the number of red and blue chips in each bag. Then, explain how you made your estimates.
Bag A
Number of red chips:
Number of blue chips:

Bag B
Number of red chips:
Number of blue chips:
Answer:
Answers will vary. Anticipate that students see Bag B as the bag with nearly the same number of blue and red chips and Bag A as possibly having a third of the chips blue. Answers provided by students should be based on the relative frequencies. A sample answer based on this reasoning is
Bag A: 4 blue chips and 8 red chips
Bag B: 6 blue chips and 6 red chips

Question 5.
In a different game of Picking Blue!, two bags each contain red, blue, green, and yellow chips. One bag contains the same number of red, blue, green, and yellow chips. In the second bag, half of the chips are blue. Describe a plan for determining which bag has more blue chips than any of the other colors.
Answer:
Students should describe a plan similar to the plan implemented in the lesson. Students would collect data by selecting chips from each bag. After several selections, the estimated probabilities of selecting blue from each bag would suggest which bag has more blue chips than chips of the other colors.

Eureka Math Grade 7 Module 5 Lesson 9 Exit Ticket Answer Key

As this is an exploratory lesson, the Exit Ticket is incorporated into the closing questions of Examining Your Results.

Engage NY Eureka Math 7th Grade Module 5 Lesson 16 Answer Key

Eureka Math Grade 7 Module 5 Lesson 16 Example Answer Key

Example 2: Using Random Numbers to Select a Sample
The histogram indicates the differences in the number of words in the collection of 150 books. How many words are typical for a best-selling children’s book? Answering this question would involve collecting data, and there would be variability in those data. This makes the question a statistical question. Think about the 150 books used to create the histogram on the previous page as a population. How would you go about collecting data to determine the typical number of words for the books in this population?

How would you choose a random sample from the collection of 150 books discussed in this lesson?

The data for the number of words in the 150 best-selling children’s books are listed below. Select a random sample of the number of words for 10 books.

Answer:
Sample response: I would add up all of the words in the 150 books and divide by 150. This would be the mean number of words for the 150 books. As the data distribution is not symmetrical, I could also find the median of the 150 books, as it would be a good description of the typical number of words. (Note: Discuss with students that using data for all 150 books is very tedious. As a result, students may indicate that selecting a random sample of the 150 books might be a good way to learn about the number of words in these children’s books.)

Sample response: I would make 150 slips of paper that contained the names of the books. I would then put the slips of paper in a bag and select 10 or 15 books. The number of pages of the books selected would be my sample.

If necessary, explain how to use ten numbers selected from a bag that contains the numbers from 1 to 150 to select the books for the sample.

If students need more direction in finding a random sample, develop the following example: Consider the following random numbers obtained by drawing slips from a bag that contained the numbers 1 to 150: {114,65,77,38,86,105,50,1,56,85}. These numbers represent the randomly selected books. To find the number of words in those books, order the random numbers {1,38,50,56,75,77,85,86,105,114}. Count from left to right across the first row of the list of the number of words, then down to the second row, and so on. The sample consists of the 1st element in the list, the 38th, the 50th, and so on.

Use the above example of random numbers to help students connect the random numbers to the books selected and to the number of words in those books.
→ What number of words corresponds to the book identified by the random number 1?
59,635; the 1st children’s book listed has 59,635 words.

→ What number of words corresponds to the book identified by the random number 38?
3,252; the 38th children’s book listed has 3,252 words.

Eureka Math Grade 7 Module 5 Lesson 16 Exercise Answer Key

Exercises 1–2

Exercise 1.
From the table, choose two books with which you are familiar, and describe their locations in the data distribution shown in the histogram.
Answer:
Answers will vary. Sample response: I read The Mouse and the Motorcycle, and that has 22,416 words. It is below the median number of words and may be below the lower quartile. Harry Potter and the Chamber of Secrets has 84,799 words. It is one of the books with lots of words but may not be in the top quarter for the total number of words.

Exercise 2.
Put dots on the number line below that you think would represent a random sample of size 10 from the number of words distribution above.

Answer:
Answers will vary. The sample distribution might have more values near the maximum and minimum than in the center.

Exercises 3–6

Exercise 3.
Follow your teacher’s instructions to generate a set of 10 random numbers. Find the total number of words corresponding to each book identified by your random numbers.
Answer:
Answers will vary. Sample response: I generated random numbers 123, 25, 117, 119, 93, 135, 147, 69, 48, 46, which produces the sample 94505, 80798, 92037, 83149, 90000, 8245, 89239, 89167, 3101, 22476.

Exercise 4.
Choose two more different random samples of size 10 from the data, and make a dot plot of each of the three samples.
Answer:
Answers will vary. One possible response is displayed below.

Exercise 5.
If your teacher randomly chooses 10 books from your summer vacation reading list, would you be likely to get many books with a lot of words? Explain your thinking using statistical terms.
Answer:
Answers will vary. Sample response: From my samples, it looks like I probably would get at least one book that had over 90,000 words because the maximum in each of the samples approached or exceeded 90,000 words. The three samples vary a lot, probably because the sample size is only 10. The median numbers of words for the three samples were about 86,000, 35,000, and 70,000, respectively, so it seems like at least half of the books would contain about 50,000 or more words.

Exercise 6.
If you were to compare your samples to your classmates’ samples, do you think your answer to Exercise 5 would change? Why or why not?
Answer:
Answers will vary. Sample response: The sample size is pretty small, so different samples might be different. I still think that I would have to read some books with a lot of words because of the shape of the population distribution.

Exercises 7–9: A Statistical Study of Balance and Grade

Exercise 7.
Is the following question a statistical question: Do sixth graders or seventh graders tend to have better balance?
Answer:
Yes, this is a statistical question because the data collected would vary between sixth and seventh graders.

Exercise 8.
Berthio’s class decided to measure balance by finding out how long people can stand on one foot.
a. How would you rephrase the question from Exercise 7 to create a statistical question using this definition of balance? Explain your reasoning.
Answer:
a. Answers will vary. Sample response: What is the typical length of time that a seventh grader can balance on one foot? The data collected to answer this question will have some variability—1 min., 2 min., 2 min. 10 sec., and so on. So, it is also a statistical question.

b. What should the class think about to be consistent in how they collect the data if they actually have people stand on one foot and measure the time?
Answer:
Sample response: Would it make a difference if students stood on their right feet or on their left? How high do they have to hold their feet off the ground? Can they do it barefoot or with shoes on? Would tennis shoes be better than shoes with higher heels? What can we use to measure the time?

Exercise 9.
Work with your class to devise a plan to select a random sample of sixth graders and a random sample of seventh graders to measure their balance using Berthio’s method. Then, write a paragraph describing how you will collect data to determine whether there is a difference in how long sixth graders and seventh graders can stand on one foot. Your plan should answer the following questions:
a. What is the population? How will samples be selected from the population? Why is it important that they be random samples?
Sample response: The populations will be all of the sixth graders and all of the seventh graders in our school. To get a random sample, we will find the number of sixth graders, say 62, and generate a list of 15 random numbers from the set 1 to 62, that is, {4,17,19,25,…}. Then, we will go into one classroom and count off the students beginning with 1 and use student 4, 17, and 19. Then we will go into the next classroom and count off the students beginning where we left off in the first room and so on. We will do the same for the seventh graders. This will give random samples because it offers every sixth and seventh grader the same chance of being selected (if using this plan with both grades).

b. How would you conduct the activity?
Answer:
Sample response: Students will stand for as long as they can using whichever foot they choose in their stocking or bare feet with their eyes open. We will time them to the nearest second using stopwatches from our science class. We will have students do the activity one at a time out in the hall so they cannot see each other.

c. What sample statistics will you calculate, and how will you display and analyze the data?
Answer:
Sample response: The sample statistics will be the mean time (in seconds) standing on one foot for the sixth graders and seventh graders. We will make a dot plot of the times for the sixth graders and for the seventh graders using parallel number lines with the same scale.

d. What would you accept as evidence that there actually is a difference in how long sixth graders can stand on one foot compared to seventh graders?
Answer:
We will compare the shape, center, and spread of the sample distributions of times for the sixth graders and do the same for the seventh graders. If the mean times are fairly close together and the spreads not that different, there is not really evidence to say one group of students has better balance.

Eureka Math Grade 7 Module 5 Lesson 16 Problem Set Answer Key

Question 1.
The suggestions below for how to choose a random sample of students at your school were made and vetoed. Explain why you think each was vetoed.
a. Use every fifth person you see in the hallway before class starts.
Answer:
Students who are not in the hallway because they have a class in another part of the building would not have a chance to be selected, so the sample would not be a random sample.

b. Use all of the students taking math the same time that your class meets.
Answer:
The students not taking math at that time would not have a chance of being selected, so the sample would not be a random sample.

c. Have students who come to school early do the activity before school starts.
Answer:
The sample would be not be a random sample because some students would not be able to get to school early, so they could not be selected.

d. Have everyone in the class find two friends to be in the sample.
Answer:
Choosing people that members of the class know would not be a random sample because people that members of the class do not know have no chance to be chosen.

Question 2.
A teacher decided to collect homework from a random sample of her students rather than grading every paper every day.
a. Describe how she might choose a random sample of five students from her class of 35 students.
Answer:
Sample response: You could assign each student a number from 1 to 35, generate five random numbers from 1 to 35, and choose the corresponding students.

b. Suppose every day for 75 days throughout an entire semester she chooses a random sample of five students. Do you think some students will never get selected? Why or why not?
Answer:
Sample response: Over that many days, it should almost even out. If you think about 375 numbers generated all together with each number from 1 to 35 having an equal chance of showing up each time, then each number should be in the overall set about 10 or 11 times. I generated 75 random samples of numbers from 1 to 35 and looked at how the numbers showed up. Every number from 1 to 35 showed up at least three times, and most of the numbers showed up about 10 or 11 times.

Question 3.
Think back to earlier lessons in which you chose a random sample. Describe how you could have used a random number generator to select a random sample in each case.
a. A random sample of the words in the poem “Casey at the Bat”
Answer:
Sample response: You could have generated the random numbers from 1 to 26 for the block of words and the random numbers 1 to 20 to choose a word in the block. Or you could number all of the words from 1 to 520 and then generate random numbers between 1 and 520 to choose the words.

b. A random sample of the grocery prices on a weekly flyer
Answer:
Sample response: Instead of cutting out all of the prices and putting them in a bag, you could just number them on the flyer and use the random number generator to select numbers to identify the items in the sample and use the price of those items.

Question 4.
Sofia decided to use a different plan for selecting a random sample of books from the population of 150 top-selling children’s books from Example 2. She generated ten random numbers between 1 and 100,000 to stand for the possible number of pages in any of the books. Then, she found the books that had the number of pages specified in the sample. What would you say to Sofia?
Answer:
Sample response: She would have to reject the numbers in the sample that referred to pages that were not in her list of 150 books. For example, if she gets the random numbers 4 or 720, she would have to generate new numbers because no books on the list had either 4 or 720 pages. She would have to throw out a lot of random numbers that did not match the number of pages in the books in the list.

It would take her a long time. But if there were no two books that had the same total number of words in the population, it would be a random sample if she wanted to do it that way. However, because there are quite a few books that have the same number of words as other books in the population, this method would not work for selecting a random sample of the books.

Question 5.
Find an example from a newspaper, a magazine, or another source that used a sample. Describe the population, the sample, the sample statistic, how you think the sample might have been chosen, and whether or not you think the sample was random.
Answer:
Responses will vary depending on the articles students find. For example, “an estimated 60% of the eligible children in Wisconsin did not attend preschool in 2009.” The population would be all of the children in Wisconsin eligible for preschool in 2009, and the sample would be the ones selected by the study. The sample statistic would be 60%. The article did not tell how the sample was chosen but said the source was from the Census Bureau, so it was probably a random sample.

Eureka Math Grade 7 Module 5 Lesson 16 Exit Ticket Answer Key

Question 1.
Name two things to consider when you are planning how to select a random sample.
Answer:
Answers will vary.

• What it means to be a random sample—that everyone in the population has the same chance to be selected.
• Is there a way to use a random number generator to make it easier to select the sample?

Question 2.
Consider a population consisting of the 200 seventh graders at a particular middle school. Describe how you might select a random sample of 20 students from a list of the students in this population.
Answer:
Answers will vary. Number the students on the list from 001 to 200. Using a random number generator, get 20 different random numbers between 001 and 200, and then select the students corresponding to those numbers on the list. It would also be correct for a student to say that she would write the 200 names on slips of paper, put them in a bag, mix them well, and then select 20 names from the bag.

Engage NY Eureka Math 7th Grade Module 5 Lesson 15 Answer Key

Eureka Math Grade 7 Module 5 Lesson 15 Exercise Answer Key

Exercises 1–5: Sampling Pennies

Exercise 1.
Do you think different random samples from the same population will be fairly similar? Explain your reasoning.
Answer:
Most of the samples will probably be about the same because they come from the same distribution of pennies in the jar. They are random samples, so we expect them to be representative of the population.

Exercise 2.
The plot below shows the number of years since being minted (the penny age) for 150 pennies that JJ had collected over the past year. Describe the shape, center, and spread of the distribution.

Answer:
The distribution is skewed with many of the pennies minted fairly recently. The minimum is 0, and the maximum is about 54 years since the penny was minted. Thinking about the mean as a balance point, the mean number of years since a penny in this population was minted seems like it would be about 18 years.

Exercise 3.
Place ten dots on the number line that you think might be the distribution of a sample of 10 pennies from the jar.

Answer:
Answers will vary. Most of the ages in the sample will be between 0 and 25 years. The maximum might be somewhere between 40 and 54.

Exercise 4.
Select a random sample of 10 pennies, and make a dot plot of the ages. Describe the distribution of the penny ages in your sample. How does it compare to the population distribution?
Answer:
Answers will vary. Sample response: The median is about 21 years. Two of the pennies were brand new, and one was about 54 years old. The distribution was not as skewed as I thought it would be based on the population distribution.

Exercise 5.
Compare your sample distribution to the sample distributions on the board.
a. What do you observe?
b. How does your sample distribution compare to those on the board?
Answer:
a. Answers will vary. Sample response: Most of them seem to have the same minimum, 0 years, but the maximums vary from about 35 to 54 years. Overall, the samples look fairly different: One median is at 25, but several are less than 10. All but two of the distributions seem to be skewed like the population (i.e., with more of the years closer to 0 than to the larger number of years).

b. Answers will vary. Sample response: It is pretty much the same as Sample 3, with some values at 0, and the maximum is 45 years. The median is around 25 years.

Exercises 6–9: Grocery Prices and Rounding
Exercise 6.
Look over some of the grocery prices for this activity. Consider the following statistical question: “Do the store owners price the merchandise with cents that are closer to a higher dollar value or a lower dollar value?” Describe a plan that might answer that question that does not involve working with all 100 items.
Answer:
Sample response: I would place all of the items in a bag. The prices in the bag represent the population. I would begin by selecting items from the bag and record the prices of each item I select. I would get a sample of at least
10 items.

Exercise 7.
Do the store owners price the merchandise with cents that are closer to a higher dollar value or a lower dollar value? To investigate this question in one situation, you will look at some grocery prices in weekly flyers and advertising for local grocery stores.
a. How would you round $3.49 and $4.99 to the nearest dollar?
b. If the advertised price was three for $4.35, how much would you expect to pay for one item?
c. Do you think more grocery prices will round up or round down? Explain your thinking.
Answer:
a. $3.49 would round to $3.00, and $4.99 would round to $5.00.
b. $1.45.
c. Sample response: Prices such as $3.95 or $1.59 are probably chosen because people might focus on the dollar portion of the price and consider the prices to be lower than they actually are when really the prices are closer to the next higher dollar amount.

Exercise 8.
Follow your teacher’s instructions to cut out the items and their prices from the weekly flyers and put them in a bag. Select a random sample of 25 items without replacement, and record the items and their prices in the table below.

Answer:
(Possible responses are shown in the table.)

Example of chart suggested:

Exercise 9.
Round each of the prices in your sample to the nearest dollar, and count the number of times you rounded up and the number of times you rounded down.
a. Given the results of your sample, how would you answer the question: Are grocery prices in the weekly ads at the local grocery closer to a higher dollar value or a lower dollar value?
b. Share your results with classmates who used the same flyer or ads. Looking at the results of several different samples, how would you answer the question in part (a)?
c. Identify the population, sample, and sample statistic used to answer the statistical question.
d. Bettina says that over half of all the prices in the grocery store will round up. What would you say to her?
Answer:
a. Answers will vary. Sample response: In our sample, we found 16 out of 25, or 64%, of the prices rounded to the higher value, so the evidence seems to suggest that more prices are set to round to a higher dollar amount than to a lower dollar amount.

b. Answers will vary. Sample response: Different samples had between 54% and 70% of the prices rounded to a higher value, so they all seem to support the notion that the prices typically are not set to round to a lower dollar amount.

c. Answers will vary. Sample response: The population was the set of all items in the grocery store flyer or ads that we cut up and put in the bag, the sample was the set of items we drew out of the bag, and the sample statistic was the percent of the prices that would be rounded up.

d. Answers will vary. Sample response: While she might be right, we cannot tell from our work. The population we used was the prices in the ad or flyer. These may be typical of all of the store prices, but we do not know because we never looked at those prices.

Eureka Math Grade 7 Module 5 Lesson 15 Problem Set Answer Key

Question 1.
Look at the distribution of years since the pennies were minted from Example 1. Which of the following box plots seem like they might not have come from a random sample from that distribution? Explain your thinking.

Answer:
Sample response: Given that the original distribution had a lot of ages that were very small, the Pennies 1 sample seems like it might not come from that population. The middle half of the ages are close together with a small interquartile range (about 12 years). The other two samples both have small values and a much larger IQR than the Pennies 1 sample, which both seem more likely to happen in a random sample given the spread of the original data.

Question 2.
Given the following sample of scores on a physical fitness test, from which of the following populations might the sample have been chosen? Explain your reasoning.

Answer:
Sample response: These sample values were not in Grades 5 or 7, so the sample could not have come from those grades. It could have come from either of the other two grades (Grades 6 or 8). The sample distribution looks skewed like Grade 6, but the sample size is too small to be sure.

Question 3.
Consider the distribution below:

a. What would you expect the distribution of a random sample of size 10 from this population to look like?
b. Random samples of different sizes that were selected from the population in part (a) are displayed below. How did your answer to part (a) compare to these samples of size 10?

c. Why is it reasonable to think that these samples could have come from the above population?
d. What do you observe about the sample distributions as the sample size increases?
Answer:
a. Sample response: The samples will probably have at least one or two elements between 80 and 90 and might go as low as 60. The samples will vary a lot, so it is hard to tell.
b. Sample response: My description was pretty close.
c. Sample response: Each of the samples is centered about where the population is centered, although this is easier to see with a larger sample size. The spread of each sample also looks like the spread of the population.
d. Sample response: As the sample size increases, the sample distribution more closely resembles the population distribution.

Question 4.
Based on your random sample of prices from Exercise 6, answer the following questions:
a. It looks like a lot of the prices end in 9. Do your sample results support that claim? Why or why not?
b. What is the typical price of the items in your sample? Explain how you found the price and why you chose that method.
Answer:
a. Sample response: Using the prices in the random sample, about 84% of them end in a 9. The results seem to support the claim.
b. Sample response: The mean price is $2.50, and the median price is $2.00. The distribution of prices seems slightly skewed to the right, so I would probably prefer the median as a measure of the typical price for the items advertised.

Question 5.
The sample distributions of prices for three different random samples of 25 items from a grocery store are shown below.
a. How do the distributions compare?

b. Thomas says that if he counts the items in his cart at that grocery store and multiplies by $2.00, he will have a pretty good estimate of how much he will have to pay. What do you think of his strategy?
Answer:
a. Sample response: The samples are slightly skewed right. They all seem to have a mean around $2.50 and a median around $2.00. Sample 1 has one item that costs a lot more than the others. Most of the prices vary from a bit less than $1.00 to around $5.00.

b. Answers will vary. Sample response: Looking at the three distributions, $2.00 is about the median, so half of the items cost less than $2.00, and half cost more, but that does not tell how much they cost. The mean would be a better estimate of the total cost because the mean is calculated in a way that is similar to how Thomas wants to estimate the total cost. In this case, the mean (or balance point) of the distributions looks like it is about $2.50, so he would have a better estimate of the total cost if he multiplied the number of items by $2.50.

Eureka Math Grade 7 Module 5 Lesson 15 Exit Ticket Answer Key

Identify each as true or false. Explain your reasoning in each case.
Question 1.
The values of a sample statistic for different random samples of the same size from the same population will be the same.
Answer:
False. By chance, the samples will have different elements, so the values of the summary statistics may be different.

Question 2.
Random samples from the same population will vary from sample to sample.
Answer:
True. Each element has the same chance of being selected, and you cannot tell which ones will be chosen; it could be any combination.

Question 3.
If a random sample is chosen from a population that has a large cluster of points at the maximum, the sample is likely to have at least one element near the maximum.
Answer:
True. If many of the elements are near the same value, it seems the chance of getting one of those elements in a random sample would be high.

Engage NY Eureka Math 7th Grade Module 5 Lesson 14 Answer Key

Eureka Math Grade 7 Module 5 Lesson 14 Exercise Answer Key

Exercises 1–2: What Is Random?

Exercise 1.
Write down a sequence of heads/tails you think would typically occur if you tossed a coin 20 times. Compare your sequence to the ones written by some of your classmates. How are they alike? How are they different?
Answer:
Students might notice a lot of variability in the sequences. Most students will have at the most two heads or two tails in a row, and few will have more than one streak of three or more. Responses might look like the following:
H T H T H T H T H T H T H T H T H T H T
T T H T H T T H T T T H H T H T H H T T

H T H H T H H T H H T H H T H H T H H T
H H T H T T H T H T T H T H T T H T H H

Exercise 2.
Working with a partner, toss a coin 20 times, and write down the sequence of heads and tails you get.
a. Compare your results with your classmates’.
b. How are your results from actually tossing the coin different from the sequences you and your classmates wrote down?
c. Toni claimed she could make up a set of numbers that would be random. What would you say to her?
Answer:
a. Students should notice that streaks of three or more heads and tails typically appear twice in the 20 tosses.
T T H T H H H H T T T T H T H H H T H T
H T H H H H H T T H T T H H T T T H T T

T H H T T T T H H T H T H T T T H T T H
H T T T H H T H T H T T T T H T H T H H

b. The results are different because when we generated the sequence, we did not have a lot of heads or tails in a row.
c. She could try, but she would probably not have some of the characteristics that a real set of random numbers would have, such as three consecutive numbers or four even numbers in a row.

Exercises 3–11: Length of Words in the Poem “Casey at the Bat”

Exercise 3.
Suppose you wanted to learn about the lengths of the words in the poem “Casey at the Bat.” You plan to select a sample of eight words from the poem and use these words to answer the following statistical question: On average, how long is a word in the poem? What is the population of interest here?
Answer:
The population of interest is all of the words in the poem.

Exercise 4.
Look at the poem “Casey at the Bat” by Ernest Thayer, and select eight words you think are representative of words in the poem. Record the number of letters in each word you selected. Find the mean number of letters in the words you chose.
Answer:
Answers will vary. Sample response: The words their, while, thousand, ball, bat, strike, muscles, and grow would have a mean of 5.25 letters.

Exercise 5.
A random sample is a sample in which every possible sample of the same size has an equal chance of being chosen. Do you think the set of words you wrote down was random? Why or why not?
Answer:
Answers will vary. Sample response: I thought it was random because I tried to use some little words and some long ones.

Exercise 6.
Working with a partner, follow your teacher’s instructions for randomly choosing eight words. Begin with the title of the poem, and count a hyphenated word as one word.
a. Record the eight words you randomly selected, and find the mean number of letters in those words.
b. Compare the mean of your random sample to the mean you found in Exercise 4. Explain how you found the mean for each sample.
Answer:
a. Sample response: We drew group 1, 12 (nine); group 1, 18 (four); group 5, 7 (seemed); group 3, 17 (in); group 23, 6 (fraud); group 27, 11 (is); group 27, 10 (air); group 16, 16 (close). The mean length of the words was 3.875.

b. Sample response: The mean of the sample from Exercise 4 is based on the length of eight words I selected. The mean of the sample in this exercise is the mean of eight words randomly selected using the method of drawing numbers to represent the group number and word number. Anticipate that for most students, the mean from the random sample is lower than the mean for the self-selected sample.

Exercise 7.
As a class, compare the means from Exercise 4 and the means from Exercise 6. Your teacher will provide a chart to compare the means. Record your mean from Exercise 4 and your mean for Exercise 6 on this chart.

Answer:
Organize the responses in a table posted in the front of the class. Have students add their means to the poster. Consider the following example:

Exercise 8.
Do you think the means from Exercise 4 or the means from Exercise 6 are more representative of the mean of all of the words in the poem? Explain your choice.
Answer:
Sample response: The means in the random sample seem to be similar. As a result, I think the means from the random sample are more representative of the words in the poem.

Exercise 9.
The actual mean of the words in the poem “Casey at the Bat” is 4.2 letters. Based on the fact that the population mean is 4.2 letters, are the means from Exercise 4 or means from Exercise 6 a better representation of the mean of the population? Explain your answer.
Answer:
Sample response: The means from the random samples are similar and are closer to the mean of 4.2. Also, the means from Exercise 4 are generally larger than the mean of the population.

Exercise 10.
How did the population mean of 4.2 letters compare to the mean of your random sample from Exercise 6 and to the mean you found in Exercise 4?
Answer:
Sample response: The mean number of letters in all of the words in the poem is 4.2, which is about four letters per word, and the mean of my random sample, 3.875, was also about four letters per word. The mean of my sample in Exercise 4 was about five letters per word.

Exercise 11.
Summarize how you would estimate the mean number of letters in the words of another poem based on what you learned in the above exercises.
Answer:
Sample response: Students should summarize a process similar to what they did in this lesson. They may simply indicate that they would number each word in the poem. They would make slips of paper from 1 to the number of words in the poem, place the slips of paper in a bag or jar, and select a sample of eight or more slips of paper. Students would then record the number of letters in the words identified by the slips of paper. As in the exercises, the mean of the sample would be used to estimate the mean of all of the words in the poem.

Eureka Math Grade 7 Module 5 Lesson 14 Problem Set Answer Key

Question 1.
Would any of the following provide a random sample of letters used in the text of the book Harry Potter and the Sorcerer’s Stone by J.K. Rowling? Explain your reasoning.
a. Use the first letter of every word of a randomly chosen paragraph.
b. Number all of the letters in the words in a paragraph of the book, cut out the numbers, and put them in a bag. Then, choose a random set of numbers from the bag to identify which letters you will use.
c. Have a family member or friend write down a list of his favorite words, and count the number of times each of the letters occurs.
Answer:
a. This is not a random sample. Some common letters, like u, do not appear very often as the first letter of a word and may tend to be underrepresented in the sample.
b. This would give you a random sample of the letters.
c. This would not be a random sample. He might like words that rhyme or that all start with the same letter. The list might also include words not in the book.

Question 2.
Indicate whether the following are random samples from the given population, and explain why or why not.
a. Population: All students in school; the sample includes every fifth student in the hall outside of class.
b. Population: Students in your class; the sample consists of students who have the letter s in their last names.
c. Population: Students in your class; the sample is selected by putting their names in a hat and drawing the sample from the hat.
d. Population: People in your neighborhood; the sample includes those outside in the neighborhood at 6:00 p.m.
e. Population: Everyone in a room; the sample is selected by having everyone toss a coin, and those that result in heads are the sample.
Answer:
a. Sample response: No. Not everyone in school would be in our hall before class. Our hall only has sixth graders in it, so the seventh and eighth graders would not have a chance to be chosen.
b. Sample response: No. Students who do not have the letter s in their last names would not have a chance to be chosen.
c. Sample response: Yes. Everyone would have the same chance to be chosen.
d. Sample response: No. People who are not in the neighborhood at that time have no chance of being selected.
e. Sample response: Yes. Everyone would have the same chance to be chosen.

Question 3.
Consider the two sample distributions of the number of letters in randomly selected words shown below:

a. Describe each distribution using statistical terms as much as possible.
b. Do you think the two samples came from the same poem? Why or why not?
Answer:
a. Answers will vary; the top distribution seems to have both a median and balance point, or mean, at 3, with a minimum of 1 letter in a word and a maximum of 7 letters. Most of the words in the sample were 2 to 4 letters long. The bottom distribution seems more skewed with the median of about 4 letters. The smallest number of letters was 2, and the largest was 10 letters. Most of the letters in this sample had between 2 and 5 letters.

b. Sample response: The samples could have come from the same poem, but the distributions seem different both with respect to shape and to measure of center, so it seems more likely that they were from two different populations.

Question 4.
What questions about samples and populations might you want to ask if you saw the following headlines in a newspaper?
a. “Peach Pop is the top flavor according to 8 out of 10 people.”
b. “Candidate X looks like a winner! 10 out of 12 people indicate they will vote for Candidate X.”
c. “Students overworked. Over half of 400 people surveyed think students spend too many hours on homework.”
d. “Action/adventure was selected as the favorite movie type by an overwhelming 75% of those surveyed.”
Answer:
a. Sample response: How were the people selected? How many people were surveyed? What were the choices, and how many did not like Peach Pop?
b. Sample response: How was the sample chosen? Were the people selected at random, or were they friends of Candidate X?
c. Sample response: Who was surveyed, and how were they selected? Was the survey given to students in a school?
d. Sample response: Was the survey given at a movie theater showing an action/adventure movie where people were there because they like that kind of movie?

Eureka Math Grade 7 Module 5 Lesson 14 Exit Ticket Answer Key

Question 1.
Write down three things you learned about taking a sample from the work we have done today.
Answer:
A random sample is one where every element in the set has an equal chance of being selected.
When people just choose a sample they think will be random, it will usually be different from a real random sample.
Random samples are usually similar to the population.

Engage NY Eureka Math 7th Grade Module 5 Lesson 13 Answer Key

Eureka Math Grade 7 Module 5 Lesson 13 Exercise Answer Key

Exercises 1–4: Collecting Data

Exercise 1.
Describe what you would do if you had to collect data to investigate the following statistical questions using either a sample statistic or a population characteristic. Explain your reasoning in each case.
a. How might you collect data to answer the question, “Does the soup taste good?”
b. How might you collect data to answer the question, “How many movies do students in your class see in a month?”
c. How might you collect data to answer the question, “What is the median price of a home in our town?”
d. How might you collect data to answer the question, “How many pets do people own in my neighborhood?”
e. How might you collect data to answer the question, “What is the typical number of absences in math classes at your school on a given day?”
f. How might you collect data to answer the question, “What is the typical life span of a particular brand of flashlight battery?”
g. How might you collect data to answer the question, “What percentage of girls and of boys in your school have a curfew?”
h. How might you collect data to answer the question, “What is the most common blood type of students in my class?”
Answer:
a. Taste a teaspoon of soup to check the seasoning.
b. Ask students to write down how many movies they have seen that month, and collect their responses.
c. Find the price of homes listed in the newspaper, and use those data to estimate the median price. Another option is to go to a realty office and get prices for the homes they have listed for sale.

d. Answers might vary depending on where students live. Students living in urban areas with high-rise apartment buildings might ask some people on each floor of the building, unless it is not a pet-friendly building, or people as they go to work in the morning; those living in suburban or rural areas might go door-to-door and ask their neighbors.

e. Ask each math teacher how many students were absent in each of her math classes for a given day.
f. Put some batteries of a particular brand in flashlights, and time how long they last.

g. Ask all students if they have a curfew. Note: Students may find it challenging to ask everyone in the school the question (especially students at large schools). Let students describe how they could use a sample (for example, asking a group of students selected at random from the school directory) to answer the question.

h. Ask students in my class about their blood type.

A population is the entire set of objects (e.g., people, animals, and plants) from which data might be collected. A sample is a subset of the population. Numerical summary values calculated using data from an entire population are called population characteristics. Numerical summary values calculated using data from a sample are called statistics.

Exercise 2.
For which of the scenarios in Exercise 1 did you describe collecting data from a population and which from a sample?
Answer:
Answers will vary depending on the responses. Students should indicate that data on how the soup tastes, median home cost, number of pets, and battery life might be collected from a sample. Data on the average number of movies, number absent from math classes, and most common blood type might be collected from the population.

Exercise 3.
Think about collecting data in the scenarios above. Give at least two reasons you might want to collect data from a sample rather than from the entire population.
Answer:
If you used the whole population, you might use it all up like in the soup and batteries examples. In some cases, a sample can give you all of the information you need. For instance, you only need a sample of soup to determine if the soup in the pot is good because it is the same all the way through. Sometimes it is too hard to collect the data for an entire population. It might cost too much or take too long to ask everyone in a population.

Exercise 4.
Make up a result you might get in response to the situations in Exercise 1, and identify whether the result would be based on a population characteristic or a sample statistic.
a. Does the soup taste good?
b. How many movies do students in your class see in a month?
c. What is the median price of a home in our town?
d. How many pets do people own in my neighborhood?
e. What is the typical number of absences in math classes at your school on a given day?
f. What is the typical life span of a particular brand of flashlight battery?
g. What percentage of girls and of boys in your school have a curfew?
h. What is the most common blood type of students in my class?
Answer:
a. “Yes, but it needs more salt.” The spoonful of soup would be similar to a statistic. (Although it is not really a “statistic,” it is based on a sample, so in that way it is like a statistic.)
b. The mean number of movies was 5; population characteristic
c. $150,000; sample statistic
d. 1 pet; either a population characteristic or a sample statistic (depending on the method used to collect the data)
e. 4 absences (mean or median representing typical); population characteristic
f. 54 hours; sample statistic
g. 65% of the girls and 58% of the boys have a curfew; either a population characteristic or sample statistic depending on the method of collecting data
h. Type O+ is the most common, with 42% of the class having O+; the class is the population, so the 42% would be a population characteristic. (It could be possible to think of the class as a sample of all seventh graders, and then it would be a sample statistic.)

Exercise 5: Population or Sample?
Indicate whether the following statements are summarizing data collected to answer a statistical question from a population or from a sample. Identify references in the statement as population characteristics or sample statistics.
a. 54% of the responders to a poll at a university indicated that wealth needed to be distributed more evenly among people.
b. Does talking on mobile phones while driving distract people? Researchers measured the reaction times of
38 study participants as they talked on mobile phones and found that the average level of distraction from their driving was rated 2.25 out of 5.
c. Did most people living in New York in 2010 have at least a high school education? Based on the data collected from all New York residents in 2010 by the U.S. Census Bureau, 84.6% of people living in New York had at least a high school education.
d. Were there more deaths than births in the United States between July 2011 and July 2012? Data from a health service agency indicated that there were 2% more deaths than births in the United States during that time frame.
e. What is the fifth best-selling book in the United States? Based on the sales of books in the United States, the fifth best-selling book was Oh, the Places You’ll Go! by Dr. Seuss.
Answer:
a. The population would be all students attending the university; poll respondents would be a sample, not the population. 54% would be a sample statistic.
b. The study participants would be a sample. All drivers would be the population; the 2.25 out of 5 would be a sample statistic.
c. The population is all of the people living in New York in 2010; the 84.6% would be a population characteristic.

d. This is a good question to discuss with students. The population would be all people in the United States, but the data probably came from a sample of the population. If necessary, point out to students that a nearly complete census of the United States did not occur in 2011 or 2012; the 2% would be a sample statistic. (Although obtaining the number of births and deaths out of everyone in the United States would be possible for 2011 or 2012, it would be very difficult and is generally done when a national census is conducted.)

e. The population would be a list of all best-selling books in the United States (using some subjective benchmark for “best”); the number of copies sold for each book would need to be known to determine the fifth best-selling book, so this is a population characteristic.

Exercises 6–8: A Census
Exercise 6.
When data are collected from an entire population, it is called a census. The United States takes a census of its population every ten years, with the most recent one occurring in 2010. Go to http://www.census.gov to find the history of the U.S. census.
a. Identify three things that you found to be interesting.
b. Why is the census important in the United States?
Answer:
a. Students might suggest (1) the idea of a census dates back to ancient Egyptian times; (2) the U.S. Constitution mandates a census every 10 years; (3) the first censuses only counted the number of men; and (4) until 1950, all of the counting was done manually.
b. According to the Constitution, the census is important for taxation purposes and in determining the number of representatives each state has in the House of Representatives. Other reasons might include planning for things such as roads and schools.

Exercise 7.
Go to the site: www.census.gov/2010census/popmap/ipmtext.php?fl=36.
Select the state of New York.
a. How many people were living in New York for the 2010 census?
b. Estimate the ratio of those 65 and older to those under 18 years old. Why is this important to think about?
c. Is the ratio a population characteristic or a statistic? Explain your thinking.
Answer:
a. 19,378,102 people
b. The ratio is 2,627,943 to 4,324,929 or about 2.6 to 4.3. It is important because when there are a greater number of older people than younger people, there are fewer workers than people who have to be supported.
c. The ratio is a population characteristic because it is based on data from the entire population of New York State.

Exercise 8.
The American Community Survey (ACS) takes samples from a small percentage of the U.S. population in years between the censuses. (www.census.gov/acs/www/about_the_survey/american_community_survey/)
a. What is the difference between the way the ACS collects information about the U.S. population and the way the U.S. Census Bureau collects information?
b. In 2011, the ACS sampled workers living in New York about commuting to work each day. Why do you think these data are important for the state to know?
c. Suppose that from a sample of 200,000 New York workers, 32,400 reported traveling more than an hour to work each day. From this information, statisticians determined that between 16% and 16.4% of the workers in the state traveled more than an hour to work every day in 2011. If there were 8,437,512 workers in the entire population, about how many traveled more than an hour to work each day?
d. Reasoning from a sample to the population is called making an inference about a population characteristic. Identify the statistic involved in making the inference in part (c).

The data about traveling time to work suggest that across the United States typically between 79.8% and 80% of commuters travel alone, 10% to 10.2% carpool, and 4.9% to 5.1% use public transportation. Survey your classmates to find out how a worker in their families gets to work. How do the results compare to the national data? What might explain any differences?
Answer:
a. The ACS obtains its results from a small percentage of the U.S. population, while the Census Bureau attempts to obtain its results from the entire population.
b. In order to plan for the best ways to travel, communities need to know how many people are using the roads, which roads, whether they travel by public transportation, and so on.
c. Between about 1,350,002 and 1,383,752 people
d. The sample statistic is \(\frac{32,400}{200,000}\), or 16.2%.

e. Answers will vary. Reasons for the differences largely depend on the type of community in which students live. Those living near a large metropolitan area, such as Washington, D.C., or New York City, may have lots of commuters using public transportation, while those living in other areas, such as Milwaukee, WI, do not have many public transportation options.

Eureka Math Grade 7 Module 5 Lesson 13 Problem Set Answer Key

Question 1.
The lunch program at Blake Middle School is being revised to align with the new nutritional standards that reduce calories and increase servings of fruits and vegetables. The administration decided to do a census of all students at Blake Middle School by giving a survey to all students about the school lunches.
http://frac.org/federal-foodnutrition-programs/school-breakfast-program/school-meal-nutrition-standards

a. Name some questions that you would include in the survey. Explain why you think those questions would be important to ask.
b. Read through the paragraph below that describes some of the survey results. Then, identify the population characteristics and the sample statistics.

About \(\frac{3}{4}\) of the students surveyed eat the school lunch regularly. The median number of days per month that students at Blake Middle School ate a school lunch was 18 days. 36% of students responded that their favorite fruit is bananas. The survey results for Tanya’s seventh-grade homeroom showed that the median number of days per month that her classmates ate lunch at school was 22, and only 20% liked bananas. The fiesta salad was approved by 78% of the group of students who tried it, but when it was put on the lunch menu, only 40% of the students liked it. Of the seventh graders as a whole, 73% liked spicy jicama strips, but only 2 out of 5 of all the middle school students liked them.
Answer:
a. Answers will vary. Possibilities include the following: How often do you eat the school lunch? Do you ever bring your lunch from home? What is your favorite food? Would you eat salads if they were served? What do you drink with your lunch? What do you like about our lunches now? What would you change? Explanations would vary but might include the need to find out how many students actually eat school lunch and if the lunches were different, would more students eat school lunch? What types of food should be served so more people will eat it?

b. Population characteristics: \(\frac{3}{4}\) eat school lunch; the median number of days is 18; 36% like bananas; 40% liked fiesta salad; 2 out of 5 liked spicy jicama strips.
Sample statistics: Tanya’s homeroom median number of days is 22; 20% liked bananas; 78% liked fiesta salad in trial; 73% of seventh graders liked spicy jicama strips.

Question 2.
For each of the following questions, (1) describe how you would collect data to answer the question, and (2) describe whether it would result in a sample statistic or a population characteristic.
a. Where should the eighth-grade class go for its class trip?
b. What is the average number of pets per family for families that live in your town?
c. If people tried a new diet, what percentage would have an improvement in cholesterol reading?
d. What is the average grade point of students who got accepted to a particular state university?
e. What is a typical number of home runs hit in a particular season for major league baseball players?
Answer:
a. All eighth-grade students would be surveyed. The result would be a population characteristic.
Possibly only students in a certain classroom or students of a particular teacher would be surveyed.
The students surveyed would be a sample, and the result would be a sample statistic.

b. Data would be collected from families responding to a survey at a local food store. Data would be a sample, and the result would be a sample statistic.

It is possible that a town is small enough to survey each family that owns a pet. If this is the case, the people surveyed would be the population, and the result would be a population characteristic.

c. Data would be collected from people at a local health center. The people surveyed using the new diet would be a sample, and the result would be a sample statistic.

It is possible that all people involved with this new diet were identified and agreed to complete the survey. The people surveyed would then be the population, and the result would be a population characteristic.

d. The data would typically come from the grade point averages of all entering freshmen at a particular state university. The result would be a population characteristic.

It may have been possible to survey only a limited number of students who registered or applied.
The students responding to the survey would be a sample, and the result would be a sample statistic.

e. This answer would come from examining the population of all major league hitters for that season; it would be a population characteristic.

Question 3.
Identify a question that would lead to collecting data from the given set as a population and a question where the data could be a sample from a larger population.
a. All students in your school
b. Your state
Answer:
a. The school might be the population when considering what to serve for school lunch or what kind of speaker to bring for an all-school assembly.

The school might be a sample when considering how students in the state did on the algebra portion of the state assessment or what percent of students engage in extracurricular activities.

b. The percent of students who drop out of school would be calculated from data for the population of all students in schools; how people were likely to vote in the coming election could use the state as a sample of an area of the country.

Question 4.
Suppose that researchers sampled attendees of a certain movie and found that the mean age was 17 years old. Based on this observation, which of the following would be most likely?
a. The mean age of all of the people who went to see the movie was 17 years old.
b. About a fourth of the people who went to see the movie were older than 51.
c. The mean age of all people who went to see the movie would probably be in an interval around 17 years of age, that is, between 15 and 19.
d. The median age of those who attended the movie was 17 years old as well.
Answer:
Answer (c) would be most likely because the sample would not give an exact value for the whole population.

Question 5.
The headlines proclaimed: “Education Impacts Work-Life Earnings Five Times More Than Other Demographic Factors, Census Bureau Reports.” According to a U.S. Census Bureau study, education levels had more effect on earnings over a 40-year span in the workforce than any other demographic factor. www.census.gov/newsroom/releases/archives/education/cb11-153.html

a. The article stated that the estimated impact on annual earnings between a professional degree and an
eighth-grade education was roughly five times the impact of gender, which was $13,000. What would the difference in annual earnings be with a professional degree and with an eighth-grade education?
b. Explain whether you think the data are from a population or a sample, and identify either the population characteristic or the sample statistic.
Answer:
a. About $65,000 a year
b. The data probably came from a sample since the report was a study and not just about the population, so the numbers are probably sample statistics.

Eureka Math Grade 7 Module 5 Lesson 13 Exit Ticket Answer Key

Question 1.
What is the difference between a population characteristic and a sample statistic? Give an example to support your answer. Clearly identify the population and sample in your example.
Answer:
A population characteristic is a summary measure that describes some feature of population, the entire set of things or objects from which data might be collected. A sample statistic is a summary measure that describes a feature of some subset of the population. For example, the population could be all of the students in school, and a population characteristic could be the month in which most of the students were born. A sample of students could be those that had mathematics during the fifth block in their schedules, and a sample statistic could be their grade point averages.

Engage NY Eureka Math 7th Grade Module 5 Lesson 12 Answer Key

Eureka Math Grade 7 Module 5 Lesson 12 Exercise Answer Key

Exercises 1–2
Exercise 1.
If the equally likely model was correct, about how many of each outcome would you expect to see if the cube is rolled 500 times?
Answer:
If the equally likely model was correct, you would expect to see each outcome occur about 83 times.

Exercise 2.
Based on the data from the 500 rolls, how often were odd numbers observed? How often were even numbers observed?
Answer:
Odd numbers were observed 228 times. Even numbers were observed 272 times.

Exercise 3.
Collect data for Sylvia. Carry out the experiment of shaking a cup that contains four balls, two black and two white, observing, and recording whether the pattern is opposite or adjacent. Repeat this process 20 times. Then, combine the data with those collected by your classmates.
Do your results agree with Philippe’s equally likely model, or do they indicate that Sylvia had the right idea? Explain.
Answer:
Answers will vary; estimated probabilities of around \(\frac{1}{3}\) for the opposite pattern and \(\frac{2}{3}\) for the adjacent pattern emerge, casting serious doubt on the equally likely model.

Exercises 4–5
There are three popular brands of mixed nuts. Your teacher loves cashews, and in his experience of having purchased these brands, he suggests that not all brands have the same percentage of cashews. One has around 20% cashews, one has 25%, and one has 35%.

Your teacher has bags labeled A, B, and C representing the three brands. The bags contain red beads representing cashews and brown beads representing other types of nuts. One bag contains 20% red beads, another 25% red beads, and the third has 35% red beads. You are to determine which bag contains which percentage of cashews. You cannot just open the bags and count the beads.

Exercise 4.
Work as a class to design a simulation. You need to agree on what an outcome is, what a trial is, what a success is, and how to calculate the estimated probability of getting a cashew. Base your estimate on 50 trials.
Answer:
An outcome is the result of choosing one bead from the given bag.
A red bead represents a cashew; a brown bead represents a non-cashew.
In this problem, a trial consists of one outcome.
A success is observing a red bead. Beads are replaced between trials. 50 trials are to be done.
The estimated probability of selecting a cashew from the given bag is the number of successes divided by 50.

Exercise 5.
Your teacher will give your group one of the bags labeled A, B, or C. Using your plan from part (a), collect your data. Do you think you have the 20%, 25%, or 35% cashews bag? Explain.
Answer:
Once estimates have been computed, have the class try to decide which percentage is in which bag. Agreeing on the 35% bag may be the easiest, but there could be disagreement concerning the 20% and 25%. If they cannot decide, ask them what they should do. Hopefully, they say that they need more data. Typically, about 500 data points in a simulation yields estimated probabilities fairly close to the theoretical ones.

Exercises 6–8
Suppose you have two bags, A and B, in which there are an equal number of slips of paper. Positive numbers are written on the slips. The numbers are not known, but they are whole numbers between 1 and 75, inclusive. The same number may occur on more than one slip of paper in a bag.

These bags are used to play a game. In this game, you choose one of the bags and then choose one slip from that bag. If you choose Bag A and the number you choose from it is a prime number, then you win. If you choose Bag B and the number you choose from it is a power of 2, you win. Which bag should you choose?

Exercise 6.
Emma suggests that it does not matter which bag you choose because you do not know anything about what numbers are inside the bags. So, she thinks that you are equally likely to win with either bag. Do you agree with her? Explain.
Answer:
Without any data, Emma is right. You may as well toss a coin to determine which bag to choose. However, gathering information through empirical evidence helps in making an informed decision

Exercise 7.
Aamir suggests that he would like to collect some data from both bags before making a decision about whether or not the model is equally likely. Help Aamir by drawing 50 slips from each bag, being sure to replace each one before choosing again. Each time you draw a slip, record whether it would have been a winner or not. Using the results, what is your estimate for the probability of drawing a prime number from Bag A and drawing a power of 2 from Bag B?
Answer:
Answers will vary.

Exercise 8.
If you were to play this game, which bag would you choose? Explain why you would pick this bag.
Answer:
Answers will vary.

Eureka Math Grade 7 Module 5 Lesson 12 Problem Set Answer Key

Question 1.
Some M&M’s^® are “defective.” For example, a defective M&M^® may have its M missing, or it may be cracked, broken, or oddly shaped. Is the probability of getting a defective M&M^® higher for peanut M&M’s^® than for plain M&M’s^®?

Gloriann suggests the probability of getting a defective plain M&M^® is the same as the probability of getting a defective peanut M&M^®. Suzanne does not think this is correct because a peanut M&M^® is bigger than a plain M&M^®, and therefore has a greater opportunity to be damaged.

a. Simulate inspecting a plain M&M^® by rolling two number cubes. Let a sum of 7 or 11 represent a defective plain M&M^® and the other possible rolls represent a plain M&M^® that is not defective. Do 50 trials, and compute an estimate of the probability that a plain M&M^® is defective. Record the 50 outcomes you observed. Explain your process.

b. Simulate inspecting a peanut M&M^® by selecting a card from a well-shuffled deck of cards. Let a one-eyed face card and clubs represent a defective peanut M&M^® and the other cards represent a peanut M&M^® that is not defective. Be sure to replace the chosen card after each trial and to shuffle the deck well before choosing the next card. Note that the one-eyed face cards are the king of diamonds, jack of hearts, and jack of spades. Do 20 trials, and compute an estimate of the probability that a peanut M&M^® is defective. Record the list of 20 cards that you observed. Explain your process.

c. For this problem, suppose that the two simulations provide accurate estimates of the probability of a defective M&M^® for plain and peanut M&M’s^®. Compare your two probability estimates, and decide whether Gloriann’s belief is reasonable that the defective probability is the same for both types of M&M’s^®. Explain your reasoning.
Answer:
a. A simulated outcome for a plain M&M^® involves rolling two number cubes. A trial is the same as an outcome in this problem. A success is getting a sum of 7 or 11, either of which represents a defective plain M&M^®. 50 trials should produce somewhere around 11 successes. A side note is that the theoretical probability of getting a sum of 7 or 11 is \(\frac{8}{36}\), or \(0 . \overline{2}\).

b. A simulated outcome for a peanut M&M^® involves choosing one card from a deck. A trial is the same as an outcome in this problem. A success is getting a one-eyed face card or a club, any of which represents a defective peanut M&M^®. 20 trials of choosing cards with replacement should produce somewhere around six successes.

c. Estimates will vary; the probability estimate for finding a defective plain M&M® is approximately 0.22, and the probability estimate for finding a defective peanut M&M^® is about 0.30. Gloriann could possibly be right, as it appears more likely to find a defective peanut M&M® than a plain one, based on the higher probability estimate.

Question 2.
One at a time, mice are placed at the start of the maze shown below. There are four terminal stations at A, B, C, and D. At each point where a mouse has to decide in which direction to go, assume that it is equally likely for it to choose any of the possible directions. A mouse cannot go backward.

In the following simulated trials, L stands for left, R for right, and S for straight. Estimate the probability that a mouse finds station C where the food is. No food is at A, B, or D. The following data were collected on 50 simulated paths that the mice took.

a. What paths constitute a success, and what paths constitute a failure?
b. Use the data to estimate the probability that a mouse finds food. Show your calculation.
c. Paige suggests that it is equally likely that a mouse gets to any of the four terminal stations. What does your simulation suggest about whether her equally likely model is believable? If it is not believable, what do your data suggest is a more believable model?
d. Does your simulation support the following theoretical probability model? Explain.
i) The probability a mouse finds terminal point A is 0.167.
ii) The probability a mouse finds terminal point B is 0.167.
iii) The probability a mouse finds terminal point C is 0.417.
iv) The probability a mouse finds terminal point D is 0.250.
Answer:
a. An outcome is the direction chosen by the mouse when it has to make a decision. A trial consists of a path (two outcomes) that leads to a terminal station. The paths are LL (leads to A), LS (leads to B), LR (leads to C), RL (leads to C), and RR (leads to D). A success is a path leading to C, which is LR or RL; a failure is a path leading to A, B, or D, which is LL, LS, or RR.

b. Using the given 50 simulated paths:

c. Paige is incorrect. The mouse still makes direction decisions that are equally likely, but there is one decision point that has three rather than two emanating paths. Based on the simulation, the mouse is more likely to end up at terminal C.

d. Yes, the simulation appears to support the given probability model, as the estimates are reasonably close.

Eureka Math Grade 7 Module 5 Lesson 12 Exit Ticket Answer Key

Question 1.
There are four pieces of bubble gum left in a quarter machine. Two are red, and two are yellow. Chandra puts two quarters in the machine. One piece is for her, and one is for her friend, Kay. If the two pieces are the same color, she is happy because they will not have to decide who gets what color. Chandra claims that they are equally likely to get the same color because the colors are either the same or they are different. Check her claim by doing a simulation.
a. Name a device that can be used to simulate getting a piece of bubble gum. Specify what outcome of the device represents a red piece and what outcome represents yellow.
b. Define what a trial is for your simulation.
c. Define what constitutes a success in a trial of your simulation.
d. Perform and list 50 simulated trials. Based on your results, is Chandra’s equally likely model correct?
Answer:
a. There are several ways to simulate the bubble gum outcomes. For example, two red and two yellow disks could be put in a bag. A red disk represents a red piece of bubble gum, and a yellow disk represents a yellow piece.
b. A trial is choosing two disks (without replacement).
c. A success is if two disks are of the same color; a failure is if they differ.
d. 50 simulated trials produce a probability estimate of about \(\frac{1}{3}\) for the same color and \(\frac{2}{3}\) for different colors.
Note: Some students may believe that the model is equally likely, but hopefully they realize by now that they should make some observations to make an informed decision. Some may see that this problem is actually similar to Exercise 3.

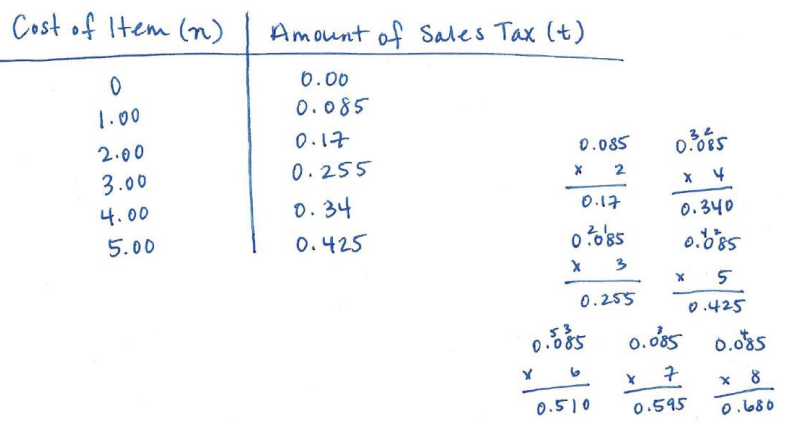
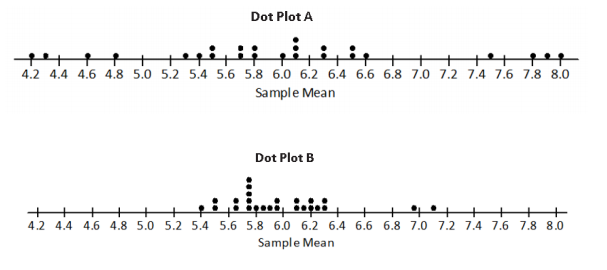
Engage NY Eureka Math 7th Grade Module 5 Lesson 11 Answer Key

Eureka Math Grade 7 Module 5 Lesson 11 Example Answer Key

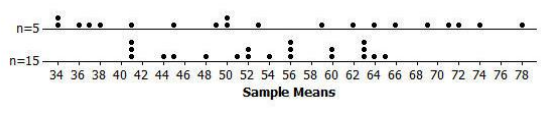
Example 1: Simulation
In the last lesson, we used coins, number cubes, and cards to carry out simulations. Another option is putting identical pieces of paper or colored disks into a container, mixing them thoroughly, and then choosing one.

For example, if a basketball player typically makes five out of eight foul shots, then a colored disk could be used to simulate a foul shot. A green disk could represent a made shot, and a red disk could represent a miss. You could put five green and three red disks in a container, mix them, and then choose one to represent a foul shot. If the color of the disk is green, then the shot is made. If the color of the disk is red, then the shot is missed. This procedure simulates one foul shot.

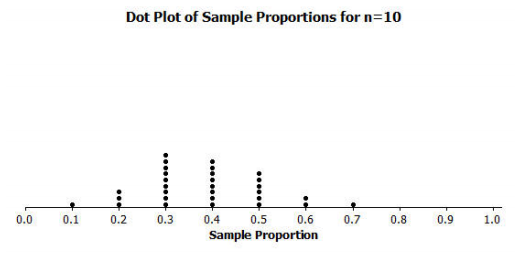
a. Using colored disks, describe how one at bat could be simulated for a baseball player who has a batting average of 0.300. Note that a batting average of 0.300 means the player gets a hit (on average) three times out of every ten times at bat. Be sure to state clearly what a color represents.
b. Using colored disks, describe how one at bat could be simulated for a player who has a batting average of 0.273. Note that a batting average of 0.273 means that on average, the player gets 273 hits out of 1,000 at bats.
Answer:
Ask students what device they would use to simulate problems in which the probability of winning in a single outcome is \(\frac{5}{8}\). A coin or number cube does not work. A deck of eight cards (with five of the cards designated as winners) would work, but shuffling cards between draws can be time-consuming and difficult for many students. Suggest a new device: colored disks in which five green disks could represent a win and three red disks could represent a miss. Put the eight disks in a bag, shake the bag, and choose a disk. Do this as many times as are needed to comprise a trial, and then do as many trials as needed to carry out the simulation. Students could also create their own spinners with eight sections, with three sections colored one color and five sections a different color, to represent the two different outcomes.
Students work on Example 1 independently. Then, discuss and confirm as a class.

a. Put ten disks in a bag, three of which are green (representing a hit), and seven are red (representing a non-hit).
b. Put 1,000 disks in a bag, 273 green ones (hits) and 727 red ones (non-hits).

Example 2: Using Random Number Tables
Why is using colored disks not practical for the situation described in Example 1(b)? Another way to carry out a simulation is to use a random number table, or a random number generator. In a random number table, the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 occur equally often in the long run. Pages and pages of random numbers can be found online.

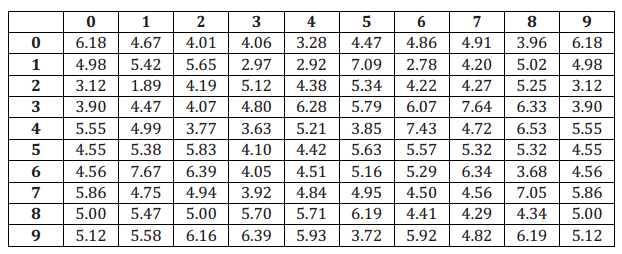
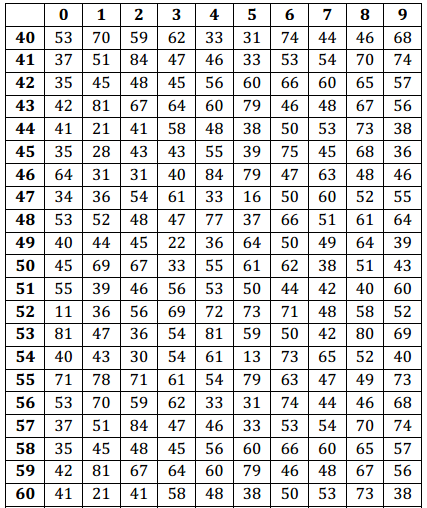
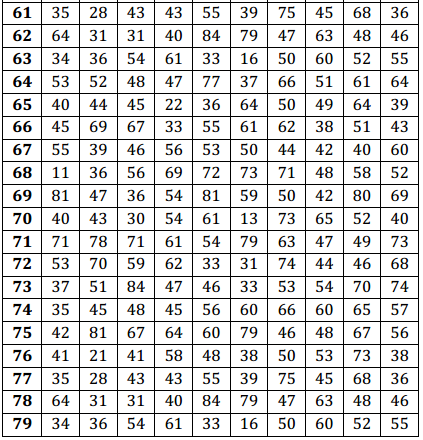
For example, here are three lines of random numbers. The space after every five digits is only for ease of reading. Ignore the spaces when using the table.

To use the random number table to simulate an at bat for the 0.273 hitter in Example 1(b), you could use a three-digit number to represent one at bat. The three-digit numbers 000–272 could represent a hit, and the three-digit numbers 273–999 could represent a non-hit. Using the random numbers above and starting at the beginning of the first line, the first three-digit random number is 252, which is between 000 and 272, so that simulated at bat is a hit. The next three-digit random number is 566, which is a non-hit.

Continuing on the first line of the random numbers above, what would the hit/non-hit outcomes be for the next six at bats? Be sure to state the random number and whether it simulates a hit or non-hit.
Answer:
The numbers are 520 (non-hit), 572 (non-hit), 597 (non-hit), 005 (hit), 621 (non-hit), and 268 (hit).

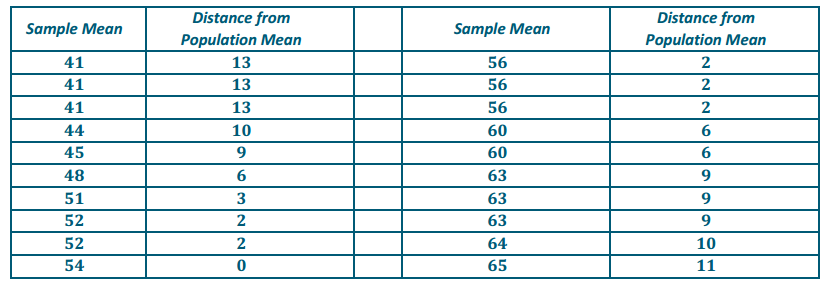
Example 3: Baseball Player
A batter typically gets to bat four times in a ball game. Consider the 0.273 hitter from the previous example. Use the following steps (and the random numbers shown above) to estimate that player’s probability of getting at least three hits (three or four) in four times at bat.
a. Describe what one trial is for this problem.
b. Describe when a trial is called a success and when it is called a failure.
c. Simulate 12 trials. (Continue to work as a class, or let students work with a partner.)
d. Use the results of the simulation to estimate the probability that a 0.273 hitter gets three or four hits in four times at bat. Compare your estimate with other groups.
Answer:
a. A trial consists of four three-digit numbers. For the first trial, 252, 566, 520, 572 constitute one trial.
b. A success is getting 3 or 4 hits per game; a failure is getting 0, 1, or 2 hits. For the first trial, the hitter got only 1 hit, so it would be a failure.
c. Answers will vary.

d. As a side note, the theoretical probability is calculated by considering the possible outcomes for four at bats that have either 4 hits (HHHH) or 3 hits (HHHM, HHMH, HMHH, and MHHH). The outcome that consists of 4 hits has probability (0.273)⁴, and each of the 4 outcomes with 3 hits has probability 4 (0.273)³ (0.727). The theoretical probability is approximately 0.0674. (Refer to Lessons 6 and 7 for the rationale for the numerical expressions.)

Example 4: Birth Month
In a group of more than 12 people, is it likely that at least two people, maybe more, will have the same birth month? Why? Try it in your class.

Now, suppose that the same question is asked for a group of only seven people. Are you likely to find some groups of seven people in which there is a match but other groups in which all seven people have different birth months? In the following exercises, you will estimate the probability that at least two people in a group of seven were born in the same month.
Answer:
Note: There is a famous birthday problem that asks, “What is the probability of finding (at least one) birthday match in a group of n people?” The surprising result is that there is a 50/50 chance of finding at least one birthday match in as few as 23 people. Simulating birthdays is a bit time-consuming, so this problem simulates birth months.

Eureka Math Grade 7 Module 5 Lesson 11 Exercise Answer Key

Exercises 1–4
Exercise 1.
What might be a good way to generate outcomes for the birth month problem—using coins, number cubes, cards, spinners, colored disks, or random numbers?
Answer:
Answers will vary; keep in mind that the first thing to do is specify how a birth month for one person is going to be simulated. For example, a dodecahedron is a 12-sided solid. Each of its sides would represent one month.

The following will not work: coins (only two outcomes), number cubes (only six outcomes, and we need 12).

The following devices will work: cards (could label twelve cards January through December), spinners (could make a spinner with twelve equal sectors), colored disks (would need 12 different colors and then remember which color represents which month), 12 disks would work if you could write the name of a month on them, and a random number table (two-digit numbers 01, 02, …, 12 would work, but 00, 13 through 99 would have to be discarded, which could be quite laborious and time-consuming).

Exercise 2.
How would you simulate one trial of seven birth months?
Answer:
Answers will vary; suppose students decide to use disks with the names of the months printed on them. To generate a trial, put the 12 disks in a bag. Then, shake the bag, and choose a disk to represent the first person’s birthday. Then, replace the disk, and do the process six more times. The list of seven birth months generates a trial.

Exercise 3.
How is a success determined for your simulation?
Answer:
A success would be at least one match in the seven.

Exercise 4.
How is the simulated estimate determined for the probability that a least two in a group of seven people were born in the same month?
Answer:
Repeat this n times, count the number of successes, and divide it by n to get the estimated probability of having at least one birth month match in a group of seven people.

Eureka Math Grade 7 Module 5 Lesson 11 Problem Set Answer Key

Question 1.
A model airplane has two engines. It can fly if one engine fails but is in serious trouble if both engines fail. The engines function independently of one another. On any given flight, the probability of a failure is 0.10 for each engine. Design a simulation to estimate the probability that the airplane will be in serious trouble the next time it goes up.
a. How would you simulate the status of an engine?
b. What constitutes a trial for this simulation?
c. What constitutes a success for this simulation?
d. Carry out 50 trials of your simulation, list your results, and calculate an estimate of the probability that the airplane will be in serious trouble the next time it goes up.
Answer:
a. Answers will vary; it is possible to use a random number table. The failure status of an engine can be represented by the digit 0, while digits 1–9 represent an engine in good status.

b. A trial for this problem would be a pair of random digits, one for each engine. The possible equally likely pairings would be 00, 0x, x0, xx (where x stands for any digit 1–9). There are 100 of them. 00 represents both engines failing; 0x represents the left engine failing, but the right engine is good; x0 represents the right engine failing, but the left engine is good; xx represents both engines are in good working order.

c. A success would be both engines failing, which is represented by 00.
d. Answers will vary; divide the number of successes by 50.

Question 2.
In an effort to increase sales, a cereal manufacturer created a really neat toy that has six parts to it. One part is put into each box of cereal. Which part is in a box is not known until the box is opened. You can play with the toy without having all six parts, but it is better to have the complete set. If you are really lucky, you might only need to buy six boxes to get a complete set. But if you are very unlucky, you might need to buy many, many boxes before obtaining all six parts.

a. How would you represent the outcome of purchasing a box of cereal, keeping in mind that there are six different parts? There is one part in each box.
b. If it was stated that a customer would have to buy at least 10 boxes of cereal to collect all six parts, what constitutes a trial in this problem?
c. What constitutes a success in a trial in this problem?
d. Carry out 15 trials, list your results, and compute an estimate of the probability that it takes the purchase of 10 or more boxes to get all six parts.
Answer:
a. Answers will vary; since there are six parts in a complete set, the ideal device to use in this problem is a number cube. Each number represents a different part.

b. Students are asked to estimate the probability that it takes 10 or more boxes to get all six parts, so it is necessary to look at the outcomes of the first 9 boxes. One roll of the number cube represents one box of cereal. A trial could be a string of 9 digits 1–6, the results of rolling a number cube.

c. A success would then be looking at the 9 digits and seeing if at least one digit 1–6 is missing. For example, the string 251466645 would count as a success, since part 3 was not acquired, whereas 344551262 would be considered a failure because it took fewer than 10 boxes to get all six parts.

d. Students are asked to generate 15 such trials, count the number of successes in the 15 trials, and divide the number by 15. The result is the estimated probability that it takes 10 or more boxes to acquire all six parts.

Question 3.
Suppose that a type A blood donor is needed for a certain surgery. Carry out a simulation to answer the following question: If 40% of donors have type A blood, what is an estimate of the probability that it will take at least four donors to find one with type A blood?
a. How would you simulate a blood donor having or not having type A?
b. What constitutes a trial for this simulation?
c. What constitutes a success for this simulation?
d. Carry out 15 trials, list your results, and compute an estimate for the probability that it takes at least four donors to find one with type A blood.
Answer:
a. With 40% taken as the probability that a donor has type A blood, a random digit would be a good device to use. For example,1, 2, 3, 4 could represent type A blood, and 0, 5, 6, 7, 8, 9 could represent non-type A blood.

b. The problem asks for the probability that it will take four or more donors to find one with type A blood. That implies that the first three donors do not have type A blood. So, a trial is three random digits.

c. A success is none of the three digits are 1, 2, 3, or 4. For example, 605 would be a success, since none of the donors had type A blood. An example of a failure would be 662.

d. Students are to generate 15 such trials, count the number of successes, and divide by 15 to calculate their estimated probability of needing four or more donors to get one with type A blood.

Eureka Math Grade 7 Module 5 Lesson 12 Problem Set Answer Key

Question 1.
Liang wants to form a chess club. His principal says that he can do that if Liang can find six players, including himself. How would you conduct a simulated model that estimates the probability that Liang will find at least five other players to join the club if he asks eight players who have a 70% chance of agreeing to join the club? Suggest a simulation model for Liang by describing how you would do the following parts.

a. Specify the device you want to use to simulate one person being asked.
b. What outcome(s) of the device would represent the person agreeing to be a member?
c. What constitutes a trial using your device in this problem?
d. What constitutes a success using your device in this problem?
e. Based on 50 trials, using the method you have suggested, how would you calculate the estimate for the probability that Liang will be able to form a chess club?
Answer:
a. Answers will vary. Using single digits in a random number table would probably be the quickest and most efficient device. 1–7 could represent “yes,” and 0, 8, 9 could represent “no.”
b. Answers will vary based on the device from part (a).
c. Using a random number table, a trial would consist of eight random digits.
d. Answers will vary; based on the above, a success is at least five people agreeing to join and would be represented by any set of digits with at least five of the digits being 1–7. Note that the random string 33047816 would represent 6 of 8 people agreeing to be a member, which is a success. The string 48891437 would represent a failure.
e. Based on 50 such trials, the estimated probability that Liang will be able to form a chess club would be the number of successes divided by 50.