Common Core Math

The concept of two-digit numbers is started with the 10 and ends with the number 99. That is 10, 11, 12, 13, 14, …………98, 99. These two-digit numbers have both tens digit and one’s digit. You might observe that after 10, the next digit will be 11 where 1 is placed after 1. The digits, 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 are changed manually to the right of digit 1. Therefore, the numbers 11, 12, 13, 14, 15, 16, 17, 18 and 19 are formed.

For example

• Numbers 10 ——– one ten.
• Number 11 ———one ten and 1 one.
• Number 12 ———-one ten and 2 ones.
• Number 13 ——— one ten and 3 ones.
• Number 20 ——— two ten.
• Number 21 ———two ten and 1 one.
• Number 22 ——— two ten and 2 ones.
  .
  .
  .
• Number 98 ——-9 ten and 8 ones.
• Number 99 ——- 9 ten and 9 ones.

So, in between the numbers from 10 to 99 are called 2 digit numbers. When the number 19 finished the next digit will start from 2 after the number 0 right to it. As mentioned above, the digits, 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 are changed manually to the right of digit 2. The number 20 has 2 tens.

Place Value of 2 Digit Numbers

In 2 Digit Numbers, there are two places present where one place is called one’s place and the other one is called 10’s place. In a 2 digit number, the left side number is at 1’s place and the right side and the right side number is at 10’s place. The one’s place digit has its original value. The digit placed at the left side ten’s place has its value ten times its original value.

Example:
23 – 3 is at one place and 2 is at tens place.
48 – 8 is at one place and 4 is at tens place.
27 – 2 is at one place and 7 is at tens place.

Also, Read:

• Place Value
• Reading And Writing Large Numbers

Addition of 2 Digit Numbers

(i) An addition of two-digit numbers, Add the one’s digits of the two numbers and then add the ten’s digits of the two numbers.
1. 10 + 20 = 30.
2. 12 + 12 = 24.
3. 22 + 15 = 37.
4. 80 + 10 = 90.
5. 50 + 30 = 80.

(ii) If you add the two-digit number with zero (0), then you will get the same two-digit number as the resultant value. That is,
25 + 0 = 25.
36 + 0 = 36.
42 + 0 = 42.
65 + 0 = 65.

(iii) If you want to add the two-digit number with the single-digit number, then you need to add this single-digit number with the one’s place digit of the 2 digit number. That is
16 + 2 = 18.
15 + 4 = 19.
20 + 2 = 22.
25 + 3 = 28.

Subtraction of 2 Digit Numbers

(i) Subtraction of 2 digit numbers also the same as the addition method. In this method Firstly, subtract the one’s place digits of the two numbers first and then subtract the ten’s place digit. That is
1. 14 – 10 = 4.
2. 25 – 12 = 13.
3. 36 – 28 = 8.
4. 48 – 24 = 24.
5. 82 – 22 = 60.

(ii) If you subtract the zero from the two-digit number, then you will get the result value of is the same two-digit number. That is,
78 – 0 = 78.
45 – 0 = 45.
66 – 0 = 66.
94 – 0 = 95.

(iii) To subtract the single-digit number from the two-digit number, you need to subtract the single digit from the one’s place digit of a two-digit number. That is,
44 – 2 = 42.
68 – 6 = 62.
82 – 8 = 74.
96 – 4 = 92.

Multiplication of Two-Digit Numbers

Multiply the one’s digit of the second number with the first number and then multiply the one’s digit of the second number with the ten’s digit of the second number. Again repeat the same process with the ten’s digit of the second number. Finally, add the values and get the resultant value. That is,
25 X 25 = 625
The resultant value of 25 X 25 is equal to 625.
25 X 15 = 375
The resultant value of 25 X 15 is equal to 375.

Conjugate Complex Numbers are the numbers that can be obtained by changing the sign of the imaginary part of the complex number. Complex numbers are the combination of both real numbers and imaginary numbers. The basic expression for the complex numbers is z= p + iq. In the above expression, ‘p’ is a real number and the ‘iq’ is an imaginary number. The value of ‘i’ is equal to √(-1.)An imaginary part of the complex numbers is denoted by either ‘i’ or ‘j’. For example, the complex number is 1 + 3i where 1 is a real number and 3i is an imaginary number.

We can find out the conjugate number for every complex number. Yes, the conjugate complex number changes the sign of the imaginary part and there is no change in the sign of the real numbers. The conjugate complex number is denoted by\(\overline {z}\) or z*.

The conjugate complex number of z is \(\overline {z}\) or z*= p – iq.

For example,

• The conjugate complex number of 1 + 3i is \(\overline {z}\) = 1 – 3i.
• The conjugate complex number of 2 + 8i is \(\overline {z}\) = 2 – 8i.
• The conjugate complex number of 10 + 5i is \(\overline {z}\)  = 10 – 5i.
• The complex conjugate number of 0.24 + 1.32i is \(\overline {z}\) = 0.24 – 1.32i.

Also, See:

• Properties of Complex Numbers

Graphical Representation of the Conjugate Complex Number

Properties of a Conjugate Complex Numbers

The basic properties of the conjugate complex numbers are mentioned below. They are

(i) \(\overline {z}\) = z

Proof: z is a complex number. that is z = p + iq.
The conjugate complex number z is \(\overline {z}\) = p – iq.
Again, the conjugate of \(\overline {z}\) is z = p + iq.

Hence, \(\overline {z}\) = z is proved.

(ii) (z₁ + z₂) ̅ = (z1) ̅ + (z2) ̅

Proof: If z₁ = p + iq and z₂ = r + is.
Then, z₁ + z₂ = p + iq + r + is.
z₁ + z₂= (p + r) + i(q + s).
The conjugate of z₁ + z₂ is  {z₁ + z₂} ̅  = (p + r) – i(q + s) ———(1).
The conjugate of z₁ is {z₁} ̅ = p – iq.
The conjugate of z₂ is {z₂} ̅  = r – is.
Now, z₁+  z₂= p – iq + r – is.
= (p + r) – i(q + s) ——-(2).
Finally, equation (1) = equation (2). (z₁ + z₂) ̅ = (z1) ̅ + (z2) ̅

(iii) (z₁ – z₂) ̅ = {z₁} ̅   – {z₂} ̅

Proof: If z₁ = p + iq and z₂ = r + is.
Then, z₁ – z₂ = (p + iq) –(r + is).
z₁ – z₂ = (p + iq – r – is)
z₁ – z₂ = (p – r) – i(q – s).
The conjugate of z₁ – z₂ is (z₁ – z₂) ̅ = (p – r) + i(q – s) ———(1).
The conjugate of z₁ is z₁  ̅= p – iq.
The conjugate of z₂ is z₂  ̅=r – is.
Now, z₁̅-  z₂̅= p – iq –(r – is).
= p – iq – r + is.
= (p – r) – i(q – s) ——-(2).
Finally, equation (1) = equation (2). That is (z₁ – z₂) ̅ = z₁̅-  z₂̅

(iv) (z₁z₂)= z₁z₂

Proof: If z₁= p + iq and z₂ = r + is.
Then, z₁*z₂ = (p + iq) * ( r + is) = pr + ips + iqr + (i)^2 qs.
i^2 = -1.
Apply the i^2 value in the above equation.
Then, we will get z₁z₂  = pr + i(ps + qr) – qs.
z₁z₂ = (pr – qs) +i(ps + qr).
The conjugate of z₁z₂ is (z₁z₂) ̅ = (pr – qs) – i(ps + qr) ———(1).
The conjugate of z₁ is (z₁) ̅ = p – iq.
The conjugate of z₂ is (z₂) ̅  = r – is.
= (p –iq) (r – is).
= pr –ips –iqr + i^2qs.
=pr – i(ps + qr) – qs.
= (pr – qs) – i(ps + qr) ———(2).
Finally, equation (1) is equal to equation (2).
(z₁z₂)=  {z₁} {z₂}

(v)(z_1//z₂) =  {z₁} {z₂} if z₂ is not equal to zero.

Proof: (z_1//z₂)=  {z₁}. {1/z₂}
We can write it as {z₁} {1/z₂}={z₁}/  {z₂}
Hence, It is proved as {(z_1//z₂)}=  {z₁}/  {z₂}

(vi) |\(\overline {z}\)| = |z|

Proof: if z = p + iq.
Then conjugate of z is \(\overline {z}\) = p – iq.
|\(\overline {z}\)|= √(p^2+(-q)^2)=√(p^2+q^2) ——-(1).
|z| = √(p^2+(q)^2) ——-(2).
So, equation (1) is equal to equation (2).
Hence, |\(\overline {z}\)| = |z| is proved.

(vii) z\(\overline {z}\)=|z|^2.

Proof: if z = p + iq, then the conjugate of z is \(\overline {z}\)= p – iq.
z\(\overline {z}\)= (p + iq) ( p – iq).
= (p^2 – ipq + ipq –(iq)^2).
= p^2 –(i)^2q^2.
i^2 = -1.
Then, z\(\overline {z}\)=p^2+q^2 ———(1).
|z| = √(p^2+q^2).
|z|^2 = (√(p^2+q^2)))^2 = p^2 + q^2 ——-(2).
Equation (1) is equal to equation (2).
So, z\(\overline {z}\)=|z|^2 is proved.

(viii) z^-1 = {z/|z|²}, where z is not equal to zero.

Proof: The given information is
z^-1 =  {z/|z|²}
we can write it as 1 / z = {z/|z|²}
So, |z|^2 = z\(\overline {z}\).
It is proved in the above property.
So, z^-1 =  {z/|z|²} is proved.

Key Points of Conjugate Complex Numbers

• z + \(\overline {z}\)= 2 real parts of (z).
• z – \(\overline {z}\)= 2 imaginary parts of (z).

Solved Examples of Conjugate Complex Number

1. Find the conjugate of the complex number z = (2 + 3i) (2 + 5i)?

Solution: The given complex number is z = (2 + 3i) (2 + 5i).
z =4 + 10i + 6i + 15(i)^2.
Substitute (i)^2 = -1 in the above expression. Then we will get
z= 4 + 16i – 15 = -11 + i16.
Now, the conjugate of the complex number z is
\(\overline {z}\)= -11 – i16.

Therefore, the conjugate of the complex number z = (2 + 3i) (2 + 5i) is equal to -11 – i16.

2. Find the conjugate of the complex number z = (1 + 3i) / (1 – 3i)?

Solution: The given complex number is z = (1 + 3i) / (1 – 3i).
Multiply the numerator and denominator with the (1 + 3i). That is,
z = (1 + 3i) (1 + 3i) / ( 1 – 3i) (1 + 3i).
z = (1 + 3i)^2 / (1)^2 – (3i)^2.
(a + b)^2 = a^2 + 2ab + b^2—–(1).
a^2 – b^2 = (a + b) (a – b)—–(2).
Substitute the equation (1) and (2) in the complex number z. That is,
z = 1 + 2(3i) + (3i)^2 / (1 + 3i) (1 – 3i).
z = 1 + 6i -9 / 1 – 3i + 3i -9i^2. {i^2 = -1}.
z = -8 + 6i / 1+9.
z = – 8 + 6i / 10.

The conjugate of complex number z is \(\overline {z}\)= – 8 – 6i / 10.

3. Find the Conjugate of the complex number 4 + 10i and explain the real and imaginary numbers?

Solution: The given information is
The complex number is 4 + 10i.
The conjugate of the complex number 4 + 10i is 4 – 10i.
Here, the real number is 4 and the imaginary number is 10i.

4. Find the conjugate of the complex number (2x + 3yi)(2x + 20yi) and identify the real and imaginary numbers?

Solution: As per the given information
The complex number is (2x + 3yi) (2x + 20yi).
(2x + 3yi) (2x + 20yi) = 4x^2 + 40xyi + 6xyi + 60y^2(i)^2.
(2x + 3yi) ( 2x + 20yi) = 4x^2 + i46xy – 60y^2. {where i=-1}.
(2x + 3yi) ( 2x + 20yi) = (4x^2 – 60y^2) + i46xy.
The conjugate of complex number (4x^2 – 60y^2) + i46xy is (4x^2 – 60y^2) – i46xy.
The real number of the complex number is (4x^2 – 60y^2).

The imaginary number of the complex number is i46xy.

5. Evaluate the expression (3 + 5i) – (8 + 2i) and find the conjugate of the expression?

Solution: The given expression is (3 + 5i) – (8 + 2i).
Expand the expression 3 + 5i – 8 – 2i.
-5 + 3i.
By evaluating the expression (3 + 5i) – ( 8 + 2i) is equal to – 5 + 3i.

The conjugate of the expression – 5 + 3i is – 5 – 3i.

6. If z = 3 + 2i, then find the z\(\overline {z}\)?

Solution: The given complex number is z = 3 + 2i.
The conjugate of the complex number z is \(\overline {z}\)= 3 – 2i.
z\(\overline {z}\)= (3 + 2i)(3 – 2i).
z\(\overline {z}\)= 9 – 6i + 6i – 4(i)^2 {if i^2 = -1}.
z\(\overline {z}\)= 9 – 4(-1).
z\(\overline {z}\)= 9 + 4 = 13.
Therefore, z\(\overline {z}\) is equal to 13 and it is a real number.

A Linear indicates the straight line. We need to find out the linear relation between the two variables. Here, the two variables are x and y. We need to draw the graph for the linear relation between x and y. The basic expression for the linear relation with two variables in mathematics is ax + by + c = 0. Here, a, b, c are constants, and x and y are variables. The constants or real numbers are a and b. These real numbers are not equal to zero and that is called a linear equation with two variables.  The below diagram is the basic diagram of the Graph of Standard Linear Relations between x and y.

Quadrants of a Graph

Generally, the graph is divided into four quadrants. In the first quadrant both the variables, x and y are positive numbers. Where the x variable values are negative and the y variable values are positive, that is called the second quadrant of the graph. In the third quadrant, both the variables x and y are negative numbers. Finally, the fourth quadrant has the y variables as negative numbers and the x variables as positive numbers. That is

• The first quadrant – x and y variables are positive.
• The second quadrant – x variable is negative and the y variable is positive.
• The third quadrant – x and y variables are negative.
• The fourth quadrant – x variable is positive and y variable is negative.

Linear Relationship with Two Variables

In this section, we are elaborating on how we can find the variable values by using the linear equation.

Plotting Points on a Graph with x and y Values.

(I) If x = 0 and y = 1, 2, -1, -2.
The given details are x = 0 and y = 1, 2, -1, -2.
The x and y variable values are mentioned on the below graph.

Here, x=0. So, all points are placed on the y- axis.

(ii) If y = 0 and x = 1, 2, -3, -6.
As per the given information y = 0 and x = 1, 2, -3, -6.

The x and y values are marked on the below graph.

All the x and y related points are marked on the x-axis only.

(iii) If x = y

The x and y variables are marked on the below graph.

Solved Examples on Linear Relationship between x and y

1. If x = 1, 2, 0, -1, -2 and the linear equation is 2x + y +1 =0, then find the y values?

Solution:
As per the given information, x = 1, 2, 0, -1, -2.
The given linear equation is 2x + y + 1 = 0.
Substitute the ‘x’ values in the above linear equation, then we will get
If x = 1
Substitute x = 1 in the linear equation 2x + y + 1 = 0.
That is, 2(1) + y + 1 = 0.
3 + y = 0.
So, y = -3.
If x = 1 then y = -3.
If x = 2.
Substitute x = 2 in the linear equation 2x + y + 1 = 0.
That is, 2(2) + y + 1 = 0.
4 + y + 1 = 0.
5 + y = 0.
So, y = -5.
If x = 2 then y = -5.
If x = 0.
Substitute x = 0 in the linear equation 2x + y + 1 = 0.
That is, 2(0) + y + 1 = 0.
y + 1 = 0.
So, y = -1.
If x = 0 then y = -1.
If x = -1.
Substitute x = -1 in the linear equation 2x + y + 1 = 0.
That is, 2(-1) + y + 1 = 0.
– 2 + y + 1 = 0.
-1 + y = 0.
So, y = 1.
So, If x = -1 then y = 1.
If x = -2.
Substitute x = -2 in the linear equation 2x + y + 1 = 0.
That is, 2(-2) + y + 1 = 0.
-4 + y + 1 = 0.
-3 + y = 0.
So, y = 3.
So, If x = -2 then y = 3.
Finally, x and y variable values are

2. Find the two variable values by using the linear equation 2x + 3y = 10?

Solution:
From the given details, the linear equation is 2x + 3y = 10.
To find out the variable values, we need to substitute the x =0 and y = 0 in the linear equation.
Firstly, apply the x = 0  in the above linear equation. That is, 2x + 3y =10.
2(0) + 3y = 10.
3y = 10.
y = 10 / 3.
Now, apply y = 0 in the linear equation. Then we will get 2x + 3y = 10.
2x + 3(0) = 10.
2x = 10.
x = 10 / 2 = 5.

Therefore, the values of the variables are x = 5 and y = 10 / 3.

3. Find the variable values by using the linear equations 2x + 5y =10 and 3x + 6y = 6?

Solution:
The given linear equations are
2x + 5y = 10——–(1).
3x + 6y = 6———(2).
Multiply the equation (1) with 3 on both sides. That is,
3 * (2x + 5y) = 10 * 3.
6x + 15y = 30——–(3).
Multiply equation (2) with 2 on both sides. That is,
2 * (3x + 6y) = 6 *2.
6x + 12y = 12——–(4).
Subtract the equation (3) and equation (4). That is
6x + 15y = 30.
6x + 12y = 12.
(-)    (-)       (-)
3y   = 18.
Y = 18 / 3 = 6.
Substitute the y = 6 in the equation (1). We will get
2x + 5y = 10.
2x + 5(6) = 10.
2x + 30 = 10.
2x = 10 – 30 = -20.
X = -20 / 2 = -10.

Therefore, the two variable values are x = -10 and y = 6.

Subtraction using 2’s Complement is an easy way to find the subtraction of numbers. Binary Subtraction is nothing but subtracting one binary number from another binary number. The Two’s Complement is the best process to works without having to separate the sign bits. The results are effectively built-into the addition/subtraction calculation using 2’s Complement method.

Check out the 2’s complement method for the binary number subtraction. We can easily subtract the binary numbers with the 2’s complement method. The expression for the 2’s complement is X – Y = X + not (Y) + 1.
For example, Y = 2 we can write it as 0010 in binary format
Not (Y) = 1101 and
Not (Y) + 1 = 1101
= 0001
Therefore, not(Y) + 1 = 1110
1110 is the 2’s complement of not(Y) + 1 where X is called as Minued and Y is called as a subtrahend.

Also, Read:

• Binary Subtraction
• Binary Addition Using 2S Complement

Conversion of Numbers into Binary Format

The very first thing, we should know the converting process of numbers into binary format. To convert the numbers into binary numbers, we have to follow one code. That is ‘8421’. Based on this code we can write the binary format numbers up to 15.

Example:
8421
0000 – 0 —-1’ s complement is 1111.
0001 – 1 —- 1’s complement is 1110.
0010 – 2 —-1’s complement is 1101.
0011 – 3 —-1’s complement is 1100.
0100 – 4 —-1’s complement is 1011.
0101 – 5 —-1’s complement is 1010.
0110 – 6 …..1’s complement is 1001.
up to 1111 = 15 —- 1’s complement is 0000.
For 2’s complement values, we need to add the ‘1’ to the 1’s complement values.
By applying the subtraction on binary numbers, we need to know some basic things like below,

• 0 – 0 = 0.
• 1 – 0 = 1.
• 0 – 1 = 1 (Borrow 1).
• 1 – 1 = 0.

How to Subtract Binary Numbers using 2’s Complement?

Follow the simple and easy steps to Perform Subtraction of Binary Numbers by 2S Complement. They are as follows

1. Note down the given numbers in the binary format.
2. Change the negative integer or number into its own 1’s complement. That means, change numbers as ‘0’ in place of ‘1’ and ‘1’ instead of ‘0’.
3. After getting the 1’s complement value of the number, add the 1 in terms of binary format to the 1’s complement value.
4. Now, the resultant value should be considered as a two’s complement of the negative integer.
5. Finally, add the two’s complement of the negative integer with the first integer value.
6. If you get the carrier that is ‘1’ by adding the above two numbers, then the result is considered positive.
7. If you won’t get the carry, then the resultant value should be considered as a negative number.

Solved Examples on Binary Subtraction by 2’s Complement

1. 1100 – 1010.

Solution:
We can write the given numbers as 1100 + (- 1010).
Step (i) The given numbers are already in binary format.
Step (ii) Change the negative integer or number or subtrahend into its own 1’s complement. That means, change numbers as ‘0’ in place of ‘1’ and ‘1’ instead of ‘0’.
The 1’s complement of 1010 is 0101.
Step (iii) Add the ’1’ to the 0101 that is 0101 + 1 = 0110.
Step (iv) 0110 is a two’s complement of – 1010.
Step (v) Minued ——1100.
Subtrahend ————1010.
Resultant value = 1   0110.

The carry number in the resultant value is ‘1’. So, the final value is a positive number. That is (+) 0110.

2. Find the value of 15 – 10 by 2’s complement?

Solution:
The given numbers are 15 – 10.
15 – 10 in terms of binary format is 1111 – 1010.
We can write it as 1111 + (-1010).
Here, 1111 is minued and the 10101 is subtrahend.
1’s complement of subtrahend is 0101.
For the 2’s complement, add the ‘1’ to the 0101. That is, 0101 + 1 = 0110.
Now, add the minued number with the 2’s complement of subtrahend number.
Minued ——-                     1111.
Subtrahend —                    0110.
The resultant value is    1  0101.

The carry number is ‘1’. So the resultant value is a positive number that is (+) 0101.

3. Calculate the subtraction of 11100 – 01100 by two’s complement?

Solution:
The given numbers are 11100 – 01100.
we can write it as 11100 + (- 01100).
Here, 11100 isminued and 01100 is subtrahend.
1’s complement of 01100 is 10011.
For the 2’s complement, add the ‘1’ to the 10011. That is 10011 + 1 = 10100.
Now, add the minued number with 2’s complement of subtrahend number.
Minued ———-                                     11100.
2’s complement of subtrahend ——-10100.
The resultant value is ——               1  10000.

The carry number is ‘1’. So the resultant value is positive. That is (+) 10000.

4. Find the subtraction by 2’s complement for 00111 – 10101?

Solution:
The given numbers are 00111 –10101.
we can write it as 00111 + (- 10101).
Here,00111 isminued and 10101 is subtrahend.
1’s complement of 10101 is 01010.
For the 2’s complement, add the ‘1’ to the 01010. That is 01010 + 1 = 01011.
Now, add the minued number with 2’s complement of subtrahend number.
Minued ———-                                     00111.
2’s complement of subtrahend ——-01011.
The resultant value is —— 10010.

There is no carry number. So the resultant value is negative. That is (-) 10010.

5. Calculate 1001.01 – 1100.10?

Solution:
The given numbers are 1001.01 – 1100.10.
we can write it as 1001.01 + (– 1100.10).
Here, 1001.01isminued and 1100.10 is subtrahend.
1’s complement of 1100.10 is 0011.01.
For the 2’s complement, add the ‘1’ to the 0011.01. That is 0011.01 + 1 = 0011.10.
Now, add the minued number with 2’s complement of subtrahend number.
Minued ———-                                     1001.01.
2’s complement of subtrahend ——-0011.10.
The resultant value is ——                   1100.11.

There is no carry number. So the resultant value is negative. That is (-) 1100.11.

6. Find the subtraction by 2’s complement for 101011 – 011001?

Solution:
The given numbers are 101011 – 011001.
We can write it as 101011 + (– 011001).
Here, 101011isminued and 011001 is subtrahend.
1’s complement of 011001 is 100110.
For the 2’s complement, add the ‘1’ to the 100110. That is 100110 + 1 = 100111.
Now, add the minued number with 2’s complement of subtrahend number.
Minued ———-                                      101011.
2’s complement of subtrahend ——- 100111.
The resultant value is ——1  110010.

The carry is ‘1’ in the resultant value. So the resultant value is positive. That is (+) 110010.

Trying to Solve Problems on Comparing Decimals and facing any difficulties? You have come to the right place where you can get a complete idea of Decimal Comparison. Learn the Step by Step Procedure to Compare Decimal Numbers and check whether they are greater or smaller. Refer to Solved Examples on Comparing Decimals explained along with detailed steps in the later sections.

How to Compare Decimal Numbers?

When comparing decimal numbers use the following steps. They are along the lines

• We know a decimal number has whole number part and decimal part. The Decimal Number with Greater whole number part is greater.
• If the Decimals you are comparing have the same number of digits in them check the value of the number without a decimal point. The Larger the Decimal Number the Closer it is to One and thus it is greater.

Also, Read:

• Decimals
• Like and Unlike Decimals
• Conversion of Unlike Decimals to Like Decimals

Comparing Decimals Examples

1. Compare 6.4 and 2.98?

Solution:

Firstly, check the whole number part in both the decimals

Since 6 >2

The Decimal Number 6.4 is greater than 2.98

2. Compare 5.45 and 5.62?

Solution:

Given Decimal Numbers are 5.45 and 5.62

In these two decimal numbers, the whole number part is the same

So we need to check the value after the decimal point

45<62

Therefore, decimal number 5.62 is greater than 5.45

3. Which is Smaller 18.02 or 18.234?

Solution:

Given Decimals are 18.02 and 18.234

Check the whole number parts, since both the whole number parts are the same check for the values next to the decimal point

.02<.234

As .234 is closer to one it is greater than .02

Thus, in the given decimals 18.02 is smaller than 18.234

4. Find the greater number 163.19 and 136.21?

Solution:

Given Decimals are 163.19 and 136.21

Check the whole number parts initially

163<136

Since the Whole Number 163 is greater the Decimal Number 163.19 is greater.

5. Find the greater number; 2332.47 or 2332.99?

Solution:

Given Decimals are 2332.47 and 2332.99

Firstly, check the whole number parts

2332=2332

As the whole number parts are the same check the values of digits after the decimal point. The number closer to one is greater

.47<.99

.99 is closer to one thus it is larger

Therefore, 2332.99 is greater.

6. Find the greater number 321.13 or 321.13?

Solution:

Given Decimal Numbers are 321.13, 32.13

Check the Whole Number Parts

321= 321

Now, check the decimal parts of the given numbers

.13 = .13

Therefore, both the decimal numbers are equal.

Learn about Changing Unlike Decimals to Like Decimals by going through this article. Know the Procedure on How to Convert, Unlike Decimals to Like Decimals explained with solved examples here. We can change Unlike Decimals to Like Decimals by simply adding the required number of Zeros on the extreme right side of the decimal so that the value doesn’t alter.

Also, See: Like and Unlike Decimals

How to Convert Unlike Decimals to Like Decimals?

We follow the Annexing Zeros on the Extreme Right Side of the Decimal Method. Follow the simple procedure listed below to change Unlike Decimals to Like Decimals. They are along the lines

• The first and foremost step is to find the decimal number having maximum number of decimal places say(n)
• Now change the decimals to their equivalent decimals that have the same number of decimal places with the highest number of decimal places.

Solved Examples on Changing Unlike Decimals to Like Decimals

1. Convert the following unlike decimals into like decimals: 83.439, 164.2, 427.23

Solution:

In the Given Decimals 83.439, 164.2, 427.23 we observe that the Decimal Number 83.439 has the maximum number of decimal places i.e. 3

Therefore, to change the given unlike decimals to like decimals we convert all of them into like decimals having three places of decimal.

83.439  is already having 3 decimal places thus it remains the same➙ 83.439

164.2 ➙ 164.200

427.23 ➙ 427.230

Therefore, 83.439, 164.200, 427.230 are all expressed as Like Decimals.

2. Covert the following unlike decimals 3.72, 24.361, 3.32, and 0.7 into like decimals?

Solution:

Given Decimal Numbers are 3.72, 24.361, 3.32, and 0.7

We observe that 24.361 has the maximum number of decimal places i.e. 3

Thus, we can change the given unlike decimals to like decimals we covert all of them into like decimals having three places of decimal

3.72 ➙ 3.720

24.361 ➙ 24.361

3.32 ➙ 3.320

0.7 ➙ 0.700

Therefore, 3.720, 24.361, 3.320, 0.700 are all expressed as Like Decimals.

3. Check whether the following decimals are like or unlike and if not so Convert them to Like Decimals?

33.04, 84.32, 105.432

Solution:

Given Decimals are 33.04, 84.32, 105.4326

We observe that the decimal number 105.432 has the maximum number of decimal places i.e. 4

Thus, we annex with zeros on the right side of the decimal part to make them all like decimals

33.04 ➙ 33.0400

84.32 ➙ 84.3200

105.4326 ➙105.4326

Therefore, 33.0400, 84.3200, 105.4326 are all expressed as Like Decimals.

4. Convert 0.4444, 147.03, 65.4 to Like Decimals

Solution:

Given Decimal Numbers are 0.4444, 147.03, 65.4

We observe the decimal number 0.4444 has the maximum number of decimal places i.e. 4

Thus, we annex with zeros on the right side of the decimal part to make them all like decimals

0.4444 ➙ 0.4444

147.03 ➙ 147.0300

65.4 ➙ 65.4000

Therefore, 0.4444, 147.0300, 65.4000 are all expressed as Like Decimals.

Are you confused about how to check if Decimal Numbers are Like or Unlike? If so, you have arrived at the right place as you will get a complete idea of the entire concept of Like and Unlike Decimals. Get to Know in detail the Like and Unlike Decimals such as Definitions, Procedure to Convert Unlike Decimals to Like Decimals, Solved Examples, etc. in the later sections.

Like and Unlike Decimals – Definitions

Decimals having the same number of decimal places i.e. decimals having the same number of digits on the right side of the decimal part are called Like Decimals.

Example: 2.35, 6.54, 7.28 are all Like Decimals

On the other hand, Decimals having a different number of decimals i.e. decimals having different digits on the right side of the decimal part are called, Unlike Decimals.

Example: 4.56, 7.854, 9.634 are Unlike Decimals

How to Check if given Decimal Numbers are Like and Unlike?

Like Decimals will have the same number of digits after the decimal point. For Example, 2.34 and 5.76 are like decimals since both the numbers have 2 decimal places after the decimal point.

Unlike Decimals will not have the same number of decimal places after the decimal point. For Example, 3.2 and 4.568 are unlike since both of them don’t have the same number of decimal places after the decimal point.

Also, Read:

• Decimals
• Decimal Fractions
• Decimal Places

How to Convert Unlike Decimals to Like Decimals?

If we place any number of annexing zeros on the right side of the extreme right digit of the decimal part of a number then the value of the number is not altered. Thus, Unlike Decimals can be converted to Like Decimals by annexing with the required number of zeros on the extreme right digit in the decimal part.

We can convert Unlike Decimals to Like Decimals by simply adding Zeros to the right of the Decimal Point or by finding the Equivalent Decimal. However, Unlike Decimals can also be equivalent decimals. For Example, 0.4, 0.40, 0.400 are all, Unlike Decimals but not equivalent decimals.

Like and Unlike Decimals Examples

1. Check if the two decimals are like or unlike: 43.47 and 53.895?

Solution:

Given Decimals are 43.47 and 53.895

Number of Decimal Places in 43.47 = 2

Number of Decimal Places in 53.895 = 3

Since both the numbers don’t have the same number of decimal places in the decimal part given decimals are unlike decimals.

2. Check if two decimals 34.5 and 547.6 are like or unlike?

Solution:

Given Decimals are 34.5 and 547.6

Number of Decimal Places in 34.5 = 1

Number of Decimal Places in 547.6 = 1

Since both the numbers have the same number of decimal places in the decimal part given decimals are like decimals

3. Convert Decimals 1.3, 4.23, 6.756 into Like Decimals?

Solution:

Given Decimals are 1.3, 4.23, 6.756

To Change the given Unlike Decimals to Like Decimals annex with a required number of zeros as placing the zeros after the right side of the decimal part will not alter the value.

Decimal Places in 1.3 = 1

Decimal Places in 4.23 = 2

Decimal Places in 6.756 = 3

To make them into like decimals annex with the required number of Zeros

Annexing with Zeros for the given decimals to make them like decimals

1.3 ➝1.300

4.23➝4.230

6.756➝6.756

Thus, given decimals changed to like decimals are 1.300, 4.230, 6.756

In this article, you will learn about the Decimal and Fractional Expansion of a Decimal Number. Before Proceeding further know the definitions of Decimal, Fraction, and the Place Value Chart. A Decimal is any number in the base 10 number system and is used to separate units place from tenths place in decimal. The decimal point present in between separates the Whole Number Part and Decimal Part.

Also, Read:

• Thousandths Place in Decimals
• Place Value
• Decimal Place Value Chart

Decimal Expansion of a Number

Decimal Expansion of a Number is its representation in the base-10 system. In this System, each decimal place consists of digits 0-9 arranged such that each digit is multiplied by a power of 10 decreasing from left to right and a decimal place with 10^0 is the one’s place.

Decimal Expansion of Number 1423.25 is defined as

1423.25 = 1*10³+4*10²+2*10¹+3*10⁰+2*10^-1+5*10^-2

= 1000+400+20+3+0.2+0.05

Decimal Expansion of a Number may terminate and in such case, the number is called a regular number or finite decimal. At times, the Decimal Expansion of a Number may become periodic and in such case, it is called a repeating decimal. However, the expansion may continue infinitely without repeating and it is called an irrational number.

Fractional Expansion of Decimals

In the Expanded Form of Decimal Fractions, you will learn how to read and write the Decimal Numbers. Decimal Numbers can be written in expanded form using the Place Value Chart.

Let us understand the same by considering an example

384.264

384.264 = 3 × 100 + 8 × 10 + 4 × 1 + 2 × \(\frac { 1 }{10 } \) + 6 × \(\frac { 1 }{100 } \) + 4 × \(\frac { 1 }{1000 } \)

= 300+80+4+\(\frac { 2 }{10 } \)+\(\frac { 6 }{100 } \)+\(\frac { 4 }{1000 } \)

Solved Examples on Decimal and Fractional Expansion

1. Write the decimal and fractional expansion of 334.252?

Solution:

In Decimal Expansion

334.252 = 3*100+3*10+4*1+2*\(\frac { 1 }{10 } \)+5*\(\frac { 1 }{100 } \)+2*\(\frac { 1 }{1000 } \)

= 300+30+4+\(\frac { 2 }{10 } \)+\(\frac { 5 }{100 } \) + \(\frac { 2 }{1000 } \)

= 300+30+4+0.2+0.05+0.002

In Fractional Expansion

= 3*100+3*10+4*1+2*\(\frac { 1 }{10 } \)+5*\(\frac { 1 }{100 } \)+2*\(\frac { 1 }{1000 } \)

= 300+30+4+\(\frac { 2 }{10 } \)+\(\frac { 5 }{100 } \) + \(\frac { 2 }{1000 } \)

2. Write the decimal and fractional expansion of 543.32?

Solution:

In Decimal Expansion

543.32 = 5*100+4*10+3*1+3*\(\frac { 1 }{10 } \)+2*\(\frac { 1 }{100 } \)

= 500+40+3+\(\frac { 3 }{10 } \)+\(\frac { 2 }{100 } \)

= 500+40+3+0.3+0.02

In Fractional Expansion

= 5*100+4*10+3*1+3*\(\frac { 1 }{10 } \)+2*\(\frac { 1 }{100 } \)

= 500+40+3+\(\frac { 3 }{10 } \)+\(\frac { 2 }{100 } \)

3. Write the Decimal and Fractional Expansion of 647.345?

Solution:

In Decimal Expansion

647.345 = 6*100+4*10+7*1+3*\(\frac { 1 }{10 } \)+4*\(\frac { 1 }{100 } \)+5*\(\frac { 1 }{1000 } \)

= 600+40+7+\(\frac { 3 }{10 } \)+\(\frac { 4 }{100 } \)+\(\frac { 5 }{1000 } \)

= 600+40+7+0.3+0.04+0.005

In Fractional Expansion

647.345 = 6*100+4*10+7*1+3*\(\frac { 1 }{10 } \)+4*\(\frac { 1 }{100 } \)+5*\(\frac { 1 }{1000 } \)

= 600+40+7+\(\frac { 3 }{10 } \)+\(\frac { 4 }{100 } \)+\(\frac { 5 }{1000 } \)

FAQ’s on Decimal and Fractional Expansion

1. What is Decimal in Expanded Form?

Expanded form notation for the decimal numbers is the mathematical expression that shows the sum of the values of each digit in the number.

2. What is the Decimal Expansion of Number 164.38?

Decimal Number 164.38 can be written in expanded form by writing it as the sum of the place value of all the digits i.e. 1*100+6*10+4*1+3*\(\frac { 1 }{10 } \)+8*\(\frac { 1 }{100 } \) = 100+60+4+0.3+0.08

3. What is the Fractional Expansion of Number 94.38?

Fractional Expansion of Number 94.38 is 9*10+4*10+3*\(\frac { 1 }{10 } \)+8*\(\frac { 1 }{100 } \) which inturn results in 90+40+\(\frac { 3 }{10 } \)+\(\frac { 8 }{100 } \)

Before we learn about the Order of a Matrix let us know What is a Matrix. Matrices are defined as a rectangular array of numbers or functions. It is a rectangular array and two- dimensional. A Matrix is a rectangular array of numbers or symbols which are generally arranged in rows and columns. The plural of matrix is matrices. The entries are the numbers in the matrix and each number is known as an element.

Order a Matrix – Definition

Basically, a two-dimensional matrix consists of the number of rows and the number of columns. The order of the matrix is defined as the number of rows and columns. The number of rows is represented by ‘m’ and the number of columns is represented by ‘n’. Therefore the order of the matrix is equal to m x n, and it is also called as ‘m by n’.

The size of the matrix is written as m x n, where m is the number of rows and n is the number of columns. For example, we have a 3 x 2 matrix, the number of rows is equal to 3, and the number of columns is equal to 2.

Different Types of Matrices

There are different types of matrices, basically categorized on the basis of the value of their elements, their order,  number of rows and number of columns, etc. Now, using different conditions, the various matrix types are categorized along with their definition.

1. Row Matrix
2. Column Matrix
3. Null Matrix
4.  Square Matrix
5. Diagonal Matrix
6. Upper Triangular Matrix
7. Lower Triangular Matrix
8. Symmetric Matrix
9. Anti- Symmetric Matrix
10. Equal Matrix
11. Singular Matrix
12. Non Singular Matrix
13. Horizontal Matrix
14. Vertical Matrix
15. Unity or identity Matrix.

Row Matrix: A Matrix having only one row is called a Row Matrix. A= [a_ij]_mxn  is a row matrix , if m=1 then row matrix is represented as A= [a_ij]_1xn . It has only one row and the order of a matrix will be 1 x n. For example, A= [1 2 4 5] is row matrix of order 1 x 4.

Column Matrix: A Matrix having only one column is called a Column Matrix. A= [a_ij]_mxn  is a column matrix, if n=1 then column matrix is represented as A= [a_ij]_mx1 . It has only one column and the order of a matrix will be m x 1. Just like row matrices had only one row, column matrices have only one column. Thus the value of the column matrix will be 1.

Null Matrix: Null Matrix is also called Zero Matrix. In a matrix all the elements are zero then it is called a Zero Matrix or Null Matrix and it is generally denoted by 0. Thus, A = [a_ij]_mxn is a Zero or Null Matrix.

Unity or Identity Matrix: If a square matrix has all elements 0 and each diagonal element is non-zero, it is called an identity matrix. It is denoted by I.

Equal Matrix: If two matrices are said to be equal if they are same order if their corresponding elements are equal to the square matrix.

Square Matrix: If the number of rows and the number of columns in a matrix are equal, then it is called Square Matrix.

How to find Order of a Matrix?

A Two- Dimensional matrix consists of the number of rows (m) and a number of columns (n). The order of the matrix is equal to m x n (also pronounced as ‘m by n’).

Order of Matrix = Number of Rows x Number of Columns.

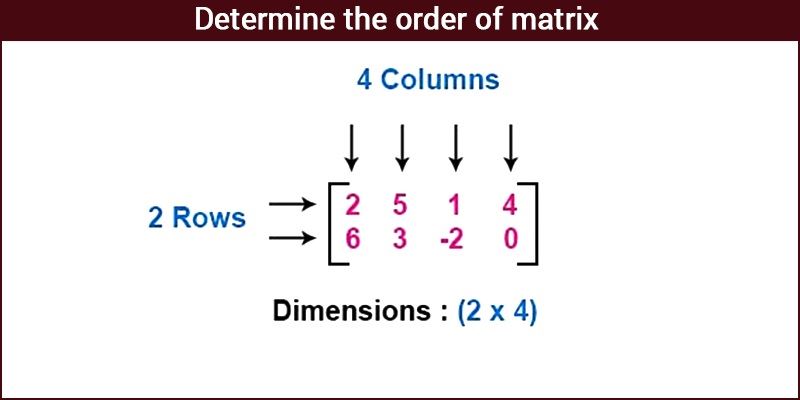
In the above, you can see, the matrix has 2 rows and 4 columns. Therefore, the order of the matrix is 2 x 4.

How will you Determine the Order of Matrix?

If a matrix has m number of rows and n number of columns, now let’s know how to find the order of the matrix.

Here few examples, how to find the order of a matrix,

[1  2  3] is an example, in this, the order of the matrix is (1 x 3), which means the number of rows (m) is 1 and the number of columns (n) is 3.

[7  5] is an example of (1 x 2) matrix, in this number of rows are (m) is 1 and number of columns (n) is 2.
\( A =\left[
\begin{matrix}
6 & 2 & 3\cr
12 & 15 & 35 \cr
\end{matrix}
\right]
\)

The order of the above matrix is (2 x 3), in this number of rows is (m) is 2, and the number of columns (n) is 3.

A matrix of the order m x n has mn elements. Hence we say that if the number of elements in a matrix is prime, then it must have one row or one column. Usually, we denote a matrix by using capital letters such as A, B, C, D, M, N, X, Y, Z, etc.

The product of m and n can be obtained in more than one ways, some of the ways are,

1. mn x 1
2. 1 x mn
3. m x n
4. n x m

Number of Elements in Matrix

Suppose, A is the order of 2 x 3. Therefore, the number of elements present in a matrix will also be 2 times 3, i.e 6.

Similarly, the other matrix order is 4 x 3, thus the number of elements will be 12 i.e. 4 times 3. If we know the order of a matrix, we can easily determine the total number of elements that the matrix has,

If a matrix is of m x n order, it will have mn element.

Order of a Matrix Examples

Example 1.

If matrix A has an 8 number of elements, then determine the order of the matrix.

Solution:

We know that number of elements is 8

Let’s write all the possible factors of the number 8

8 = 1 x 8

8 = 4 x 2

8 = 2 x 4

8 = 8 x 1

we can get the number 8 is four ways.

Therefore, there are four possible ways or orders of the matrix with 8 number of elements are 1 x 8, 2 x 4, 4 x 2, and 8 x 1.

Example 2.

If a matrix X has 7 number of elements, find the order of the matrix.

Solution:

We know that number of elements is 7

Let’s write all the possible factors of the number 7

7 = 1 x 7

7= 7 x 1

we can get the number 7 in two ways.

Therefore, there are two possible ways or orders of the matrix with 7 number of elements are 1 x 7, 7 x 1.

Example 3.

What is the order of a matrix given below?

Solution:

The number of rows in a given matrix is A = 2

The number of columns in a given matrix is A = 3

Therefore, the order of matrix is  2 x 3.

Example 4.

What is the order of a matrix given below?

Solution:

The number of rows in a given matrix is A = 3

The number of columns in a given matrix is A = 3

Therefore, the order of the matrix is 3 x 3.

FAQ’s on Order of Matrix

1. What is Matrix and Types?

A Matrix can be defined as a rectangular array of numbers or functions. A matrix consists of rows (m) and columns (n) that is m x n. Types of Matrices are :

1. Row Matrix
2. Column Matrix
3. Null Matrix
4. Equal Matrix
5. Unity or Identity Matrix
6. Square Matrix
7. Rectangular Matrix
8. Horizontal Matrix
9. Vertical Matrix
10. Scalar Matrix

2. What is the Null Matrix?

Null Matrix is also called Zero Matrix. In a matrix all the elements are zero then it is called a Zero Matrix or Null Matrix and it is generally denoted by 0. Thus, A = [a_ij]_mxn is a Zero or Null Matrix.

3. What is another name of Unity Matrix?

Another name of the unity matrix is Identity Matrix. If a square matrix has all elements 0 and each diagonal element is non-zero, it is called an Identity Matrix. It is denoted by I.

4. What is the order of Square Matrix?

A Matrix that has a number of rows is equal to a number of columns is called Square Matrix. In this matrix, all the elements are arranged in m number of rows and n number of columns . So the order of the matrix is denoted by mxn.

5. Explain a Scalar Matrix?

Scalar Matrix is similar to a square matrix. In the scalar matrix, all off-diagonal elements are equal to zero and all on diagonal elements happen to be equal. In other words, the Scalar Matrix is an identity matrices multiple.

Are you searching for a tool that computes the addition of two binary numbers using 1’s complement method? If yes, then you have reached the correct place. Here we are giving the detailed steps on how binary addition of two numbers with 1s complement. You can also get Binary Addition Using 1s Complement definition, how to get 1s complement of a binary number, and example questions to improve the levels of understanding.

What is Binary Addition?

A binary number is a number with the base 2. Binary addition is one of the basic arithmetic operations. The binary system has only two digits 0 and 1. The binary code uses the digits 0’s and 1’s to make certain processes turn on or off. The process of the binary addition operation is very familiar to the decimal system by adjusting to the base 2.

Before attempting the binary addition, you must have complete knowledge of how the place works in the binary number system. Almost all modern digital computers and electronic circuits perform the binary operation by representing each bit as a voltage signal. The binary bit 0 means OFF state, 1 means ON state.

1’s Complement of a Binary Number

We have a simple algorithm to convert a binary number into 1’s complement. To get 1’s complement of a binary number, invert the given binary number. You can also implement a logic circuit using only NOT gate for each bit of binary number input.

Example:

Calculate the 1’s complement of a binary number 10101110

Invert each bit of a given binary number

So, 1’s complement of 10101110 is 01010001.

Also, Read

• Binary Addition using 2’S Complement
• Binary Subtraction
• Hexadecimal Addition and Subtraction

Binary Addition Using 1’s Complement

Binary addition means simply performing an addition operation between two binary numbers. You can add two binary numbers digit by digit just like decimal numbers. The rules for adding two binary digits is 0 + 0 = 0, 1 + 0 = 1, 0 + 1 = 1, 1 + 1 = 10(1 is carry). At first, convert the given numbers to the 1’s complement and add those numbers using thee rules. Also, have a look at the detailed process on how to add binary numbers using 1’s complement in the following section.

How to do Binary Addition Using 1s Complement?

The process of adding binary numbers purely depends on their sign and magnitude. Here are the different cases.

Case I: Adding a positive and a negative number. If the positive number has a greater magnitude

Here, the addition of numbers is performed after taking 1’s complement of the negative number, and at the end round carry of the sum is added to the LSB (least significant bit).

Example: + 1101 – 1011

+ 1101 ⇒ 0 1 1 0 1

– 1011 ⇒ 1 0 1 0 0 (1’s complement)

⇒ 0 0 0 0 1 + 1 = 0 0 0 1 0

Hence the sum is +0010.

Case II: If the negative number has a greater magnitude

Here the addition is done in the same way as in case I but there will be non-end-around carry. The sum is obtained by taking the 1’s complement of the magnitude bits of the result and the sum is negative.

Example: 1011 – 1101

+ 1 0 1 1 ⇒ 0 1 0 1 1

– 1 1 0 1 ⇒ 1 0 0 1 0 (1’s complement)

⇒ 1 1 1 0 1

The sum is 1’s complement of 1101

Hence the sum is – 0010.

Case III: If two binary numbers are negative.

To add two negative binary numbers, 1’s complements of both the numbers are taken later addition is performed. In this case, an end-around carry will always appear. This along with a carry from the MSB will generate a 1 in the sign bit. 1’s complement of the magnitude bits of the result of an addition will give the final sum.

Example: -0110 and -0111

– 0 1 1 0 ⇒ 1 1 0 0 1 (1’s complement)

– 0 1 1 1 ⇒ 1 1 0 0 0 (1’s complement)

⇒ 1 0 0 0 1 + 1 = 1 0 0 1 0

1’s complement of 0010 is 1101 and the sign bit is 1

Hence the sum is -1101.

Binary Addition Using 1s Complement Examples

Example 1:

Calculate the sum of 0100, -1000 using the 1’s complement.

Solution:

The given binary numbers are 0100, -1000

1’s complement of -1000 is 10111

0 0 1 0 0 + 1 0 1 1 1 = 1 1 0 1 1

1’s complement of 1011 is 0100

Hence the sum is -0100.

Example 2:

Find the sum of 10000, -00111 using the 1’s complement.

Solution:

The given binary numbers are 10000, -00111

Find the 1’s complement of the negative number i.e 00111

1’s complement of 000111 = 111000

010000 + 111000 = 1 0 0 1 0 0 0

0 0 1 0 0 0 + 1 = 0 0 1 0 0 1

Hence, the sum is 001001.

Example 3:

Find the sum of -0100, -0010 using the 1’s complement method.

Solution:

The given numbers are -0100, -0010

Find the 1’s complement of the negative numbers

1’s complement of 0100 is 1011

1’s complement of 0010 is 1101

1 0 1 1 + 1 1 0 1 = 1 1 0 0 0

1 1 0 0 0 + 1 = 1 1 0 0 1

1’s complement of 1 0 01 is 0 1 1 0 and 1 is the sign bit

Hence, the sum is -0110

Example 4:

Find the sum of 1000 and -0101 using the 1’s complement.

Solution:

The given binary numbers are 1000 and -0101.

Find the 1’s complement of the negative number

1’s complement of 0101 is 11010.

0 1 0 0 0 + 1 1 0 1 0 = 1 0 0 0 1 0

1 0 0 0 1 0 + 1 = 1 0 0 0 1 1

Hence the sum is 00011.

FAQ’s on Binary Addition using 1’s Complement

1. How to find 1’s complement of a binary number?

To get the 1’s complement of binary numbers, just invert the number. Inversion means placing 1’s in place of 0’s and 0’s in place of 1’s. Otherwise, you can also use NOT logic gate to find the 1’s complement.

2. How to add two negative binary numbers using the 1’s complement?

For adding two negative binary numbers with the 1’s complement, just find the 1’s complement of both numbers. Add those 1’s complement numbers and add 1 to the obtained result. Then you will get 1 in place of the sign bit. Get the 1’s complement of the obtained sum to get the final result.

3. What’s the purpose of using complements in binary number operations?

Compared to other systems for representing the signed numbers 1’s complement, 2’s complement has the advantage that the fundamental arithmetic operations are identical to those for unsigned binary numbers.

The equation of a straight line represents each and every point on that line. Let us consider the straight line created by passing through the two points such as (a1, b1) and (a2, b2). There are no curves present in the straight line. The basic equation for the straight line in Two-point for is ax + by + c = 0. Here, a, b, c are constants, and x and y are variables.

How to find the Equation of a Straight Line Passing Through Two Points?

The below diagram shows the straight line in two-point form. In this, (a1, b1) is the starting point of the straight line, and (a2, b2) is the ending point of the straight line.

The equation of the straight line which is passing through the two points A(a1, b1) and B(a2, b2) is b – b1 = (b2 – b1) / (a2 – a1) * (a – a1). P(a, b)is the joining point of A and B.
The straight line is passing through the two points A and B. Then the slope of the line AB = (b1 – b2) / (a1- a2).———( 1 ).
Now, the straight line is passing through the two – points A and P. Then the slope of the line AP = (b – b1) / (a – a1). ——- ( 2 ).
To find out the equation of a straight line with two point form, we need to equate the two equations. That is,
Slope of the line AP = Slope of the line AB.
(b – b1) / (a – a1) = (b1 – b2) / (a1 – a2).
(b – b1) = (b1 – b2) / (a1 – a2) * (a – a1).
Equation for the straight line of two – point form is equal to (b – b1) = (b1 – b2) / (a1 – a2) * (a – a1).
Let us consider the slope (b1 – b2) / (a1 – a2) as ‘m’. substitute the value in the above equation. Then straight line equation becomes as
(b – b1) = m(a – a1).

Steps to Solve Equation of the Straight Line Problems

Follow the three steps to find the Equation of the Straight Line. They are

1. Find the slope of the line.
2. Put the slope and one point into the “Point-Slope Formula”.
3. Simplify the equation.

Also, See:

• Angle Between Two Straight Lines

Two – Point Form Examples with Solutions

1. Find the Equation of the straight line passing through the points (1, 2), and (3, -2)?

Solution:
The given details are (a1, b1) = (1, 2) and (a2, b2) = (3, -2).
The equation for the straight line is (b – b1) = (b1 – b2) / (a1 – a2) * (a – a1).
Substitute the values in the above equation, then we will get
(b – 2) = (2 – (-2)) / (1 – 3) * (a – 1).
(b – 2) = (2 + 2) / (-2) * (a – 1).
(b – 2) = 4 / (-2) * (a – 1).
(b – 2) = -2 * ( a – 1).
b – 2 = -2a + 1.
2a + b – 2 -1 = 0.
2a + b – 3 = 0.

Finally the straight line equation is 2a + b – 3 = 0.

2. Find the equation of the straight line joining the points (-2, 4) and (5, 6)?

Solution:
As per the given information, the straight line is created by joining the two – points. They are (a1, b1) = (-2, 4) and (a2, b2) = (5, 6).
Equation for the straight line of joining two points is (b – b1) = (b1 – b2) / (a1 – a2) * (a – a1).
Substitute the values in the above equation, then we will get like
(b – 4) = (4 – 6) / (-2 – 5) * (a – (-2)).
(b – 4) = (- 2 / – 7) *(a + 2).
(b –4) (7) = 2 * (a + 2).
7b – 28 = 2a + 4.
-2a + 7b – 28 – 4 = 0.
-2a + 7b -32 = 0.

Therefore, the final equation for the straight line is -2a +7b – 32 = 0.

3. Find the straight-line equation with the help of two points (6, 2) and (8, 4)?

Solution:
The given information is the straight line is crossing the two points. They are (a1, b1) = (6, 2) and (a2, b2) = (8, 4).
The equation for the straight line in Two – point form is (b – b1) = (b1 – b2) / (a1 – a2) * (a – a1).
Substitute the values in the above equation, we will get
(b – 2) = (2 – 4) / ( 6 – 8) * ( a – 6).
(b – 2) = ( – 2) / ( – 2) * (a – 6).
(b – 2) = (a – 6).
-a + b – 2 + 6 = 0.
-a + b + 4 = 0.
a – b – 4 = 0.

Finally, the equation for the straight line in two – points is equal to a – b – 4 = 0.

4. Find the equation of a straight line that is passing through points A(6, 6) and B(10, 4)?

Solution:
As per the given information, the straight line is passing through the two points. They are
(a1, b1) = (6, 6) and (a2, b2) = (10, 4).
The basic equation for the straight line in two – point form is (b – b1) = (b1 – b2) / (a1 – a2) * (a – a1).
Substitute the above values in the equation. Then we will get like
(b – 6) = (6 – 4) / (6 – 10) * (a – 6).
(b – 6) = 2 / (-4) * (a – 6).
(b – 6) = 1 / (-2) * (a – 6).
-2 ( b – 6) = a – 6.
-2b + 12 = a – 6.
-a – 2b + 12 + 6 = 0.
a + 2b – 18 = 0.

Finally the equation for the straight line is a + 2b – 18 = 0.

5. Find the values of a for which the points A(a, -2), B(4, 2) and C(8, 10) are collinear?

Solution:
As per the given information, the given points A(a, -2), B(4, 2), and C(8, 10) are collinear.
(a, b) = (a, -2), (a1, b1) = (4, 2), and (a2, b2) = (8, 10)
So, the slope of the AB = slope of the BC.
(b1 – b) / (a1 – a) = (b2 – b1) / (a2 – a1).
Substitute the values in the above equation. Then we will get
(2 – (-2)) / ( 4 – a) = (10 – 2) / (8 – 4).
(2 + 2) / (4 – a) = 8 / 4.
4 / (4 – a) = 2.
4 = 2(4 – a).
4 – a = 2.
4 – 2 = a.
a = 2.

Finally, a is equal to 2.

A Decimal Number consists of a whole number part and a fractional part separated by a decimal point. If you wish to learn completely about Decimal Places and How to Learn to Count Decimal Places. Know about Decimal Place Value Chart Definition, Facts, Solved Examples in the further modules. We are sure you will be familiar with the Decimal Places by the end of this article.

What is meant by Decimal Places?

A Decimal Number consists of both whole number part and decimal number part. The digits right to the decimal point are called the Decimal Part and the digits left to the decimal point are called the whole number part. The Number of Digits present in the decimal part of the given decimal number is known as Decimal Places.

Based on the position of the digit in the number it has a value named place value. For Example, the Place Value of the digit 2 in 1234.45 is 200 as 2 is in the hundreds place. However, if you interchange the digits 3 and 2 we get a new number i.e. 1324.45. In 1324.45 the place value of a digit is 20 as it is in the tens place.

How to Learn to Count Decimal Places?

The number of digits present in the decimal part of the given decimal number is nothing but the Decimal Places. Check out the below-listed examples to understand how to read and count the decimal places for the given decimal number.

For Example:

Decimal Number 5.34 has 2 decimal places.

Decimal Number 0.376 has 3 decimal places.

The Number 86.261 has 3 decimal places.

The Number 912.67 has 2 decimal places.

To better understand the Decimal Numbers you need to be aware of the Place Value.

For Example Decimal Number 51.048053 Place Value is explained clearly below.

In the above-illustrated example, 51 is the whole number part and 048053 is the decimal or fractional part.

Whole Number Part

Place of 1 is Ones and its place value is 1

Place of 5 is Tens and its place value is 50

Decimal Number Part

Place of 0 is Tenths and its place value is 0*\(\frac { 1 }{ 10 } \) = 0

Place of 4 is hundredths and its place value is 4*\(\frac { 1 }{ 100 } \) = \(\frac { 4 }{ 100 } \) = 0.04

Place of 8 is Thousandths and its place value is 8*\(\frac { 1 }{ 1000 } \) = \(\frac { 8 }{ 1000 } \) = 0.008

Place of 0 is Ten Thousandths and its place value is 0*\(\frac { 1 }{ 10,000 } \) = 0

Place of 5 is Hundred Thousandths and its place value is 5*\(\frac { 1 }{ 100,000 } \) = \(\frac { 5 }{ 100,000 } \) = 0.00005

Place of 3 is Millionths and its place value is 3*\(\frac { 1 }{ 1000000 } \) = \(\frac { 3 }{ 1000000 } \) = 0.000003

= 5*10+1*1+0*10^-1+4*10^-2+8*10^-3+0*10^-4+5*10^-5+3*10^-6

= 51.048053

FAQs on Decimal Places

1. What are Decimal Places?

Decimal Places are nothing but the number of digits next to the decimal point or in the decimal part.

2. How do you find the Decimal Places?

Firstly, count the number of digits after the decimal point and the number itself tells the Decimal Places for a particular decimal number.

3. How many decimal places are there in the Decimal Number 32.4356?

The number of Decimal Places in the Decimal Number 32.4356 is 4.

Before recalling about Decimal Fraction let us learn the fundamentals of what is a fraction. A fraction is formed up of two parts namely numerator and denominator. A Decimal Fraction is a Fraction having a denominator of 10 or multiples of 10 such as 100, 1000, 10000, …., etc. This article helps you to be well versed with Decimals Fractions such as Definitions, Facts, Operations performed on Decimal Fractions, Solved Examples.

What is a Decimal Fraction?

A Decimal Fraction is a Fraction in which the denominator is a power of 10 such as 10, 100, 1000, etc. You can write Decimal Fractions with a Decimal Point instead of a Denominator. By expressing the decimal fractions using decimal point calculations of addition, subtraction, multiplication, and division will be much simpler.

Examples:

\(\frac { 13 }{ 100 } \) = 0.13

\(\frac { 54 }{ 10 } \) = 5.4

Also, See:

• Conversion of a Decimal Fraction into a Fractional Number
• Decimals
• Converting Decimals to Fractions

Operations on Decimal Fractions

Addition and Subtraction of Decimal Fractions: Given Numbers are placed under each other so that the decimal points lie in each column and below one another. Later, the numbers are added and subtracted in a regular way.

For Example:

Add 0.0045 and 3.0423

The Sum of 0.0045 and 3.0423 is 3.0468

Multiplication of Decimal Fractions: Multiply the given numbers without considering the decimal point. After that, the decimal point is marked off to obtain the decimal places that is the sum of decimal places in the given numbers.

For Example 0.3*0.03*0.003

Multiply the numbers without considering the decimal point

3*3*3 = 27

Now find the number of decimal places to be marked by adding the decimal places in the given numbers i.e. (1+2+3) = 6 i.e. 0.000027

Dividing Decimal Fraction by a Counting Number: Divide the given number without considering the decimal point by counting the number. Later, after obtaining the quotient place as many decimal places are there in the dividend. If we were to divide 0.0028÷7 we will firstly divide 28÷7 and the quotient is 4. As there are 4 decimal places in the given number place the same in quotient obtained i.e. 0.0004

Thus, 0.0028÷7 = 0.0004

Dividing Decimal Fraction by a Decimal Fraction: Multiply both the dividend and divisor with suitable powers of 10 so that you can make them as a whole number and then proceed.

Thus, \(\frac { 0.00077 }{ 0.11 } \) = \(\frac { 0.00077*100 }{ 0.11*100 } \)

= \(\frac { 0.077 }{ 11 } \)

= 0.007

Solved Examples on Decimal Fractions

1. Convert (i) 0.60 and (ii) 4.008 into vulgar fractions?

Solution:

(i) 0.60 = \(\frac { 60 }{ 100 } \) = \(\frac { 3 }{ 5 } \)

(ii) 4.008 = \(\frac { 4008 }{ 1000 } \) = \(\frac { 501 }{ 125 } \)

In order to convert decimal into vulgar fractions firstly place 1 in the denominator and annex with as many zeros as the number of digits after the decimal point in the given number. Later, remove the decimal point and note the whole number in the numerator. Reduce it to Lowest Form. Remember Annexing Zeros to the Right of Decimal Fraction doesn’t change the value.

2. Add 35.2 + 4.098?

Solution:

Given Numbers are placed under each other so that the decimal point lies in one column. Numbers can be subtracted or added in a usual way.

3. Evaluate i) 5.3029×100

Solution:

i) 5.3029×100

To Multiply a Decimal Fraction by a Power of 10 shift the decimal point to the right as many places of decimal that is to the power of 10.

5.3029×100 = 530.29

4. Find the product

i) 2.232×0.1

Simply multiply the numbers without considering the decimal point. i.e. 2232*1= 2232

Later, count the number of decimal places in the given numbers i.e. (3+1) = 4

Now put the decimal after 4 that counts 4 digits from right thus 0.02232

5. Evaluate 0.81÷ 9?

Solution:

Divide the given number as if there is no decimal point. 81÷9 = 9

After obtaining the quotient count the number of decimal places in the given number i.e. 0.81 =2

Hence place the decimal point on the left of 0.09

Looking for ways on How to Add Mixed Fractions? If so, halt your search as we have listed all about Mixed Fractions Addition and different methods of it clearly in the later modules. Mixed Fractions are one of the types of fractions. These are also called Mixed Numbers. Go through the entire article to be well versed with the details like Adding Mixed Fractions Definition, How to Add Mixed Fractions with Same and Different Denominators, Examples, etc.

Mixed Fraction – Definition

A Mixed Fraction is a form of a fraction that has a whole number next to a fraction.

Example: 3 \(\frac { 1 }{ 5 } \) where 3 is a whole number and \(\frac { 1 }{ 5 } \) is a fraction.

How to Add Mixed Numbers?

When it comes to Adding Mixed Fractions we can have either the same or different denominators for both the fractions to be added. There are two different methods for Adding Mixed Numbers with Like, Unlike Denominators. Here is a Step by Step Procedure on How to Add Mixed Fractions. They are as such

Method 1: Adding the Whole Numbers and Fractions Separately

• In the first step add the whole numbers separately.
• In order to add fractions with the same denominator, simply add the numerators and keep the denominator unaltered. However, if you have different or unlike denominators take the LCM of them and change to Like Fractions.
• Once, you have a Common Denominator adding fractions is much simpler.
• Find the Sum of Whole Numbers and Fractions in Simplest Form.

Method 2: Convert Mixed Numbers to Improper Fractions and then Add them

• Initially, change the given Mixed Fractions to Improper Fractions.
• If Denominators of the Improper Fractions are the same simply add the numerators. If the Denominators of Improper Fractions are Unlike or Different take the LCM of Denominators and change them to like fractions.
• Add Like Fractions and express the sum to its Simplest Form.

Also, Check:

• Like and Unlike Fractions
• Equivalent Fractions
• Types of Fractions

Examples on Adding Mixed Fractions using Method 1

1. Add 3 \(\frac { 1 }{ 3 } \), 2 \(\frac { 1 }{ 4} \)?

Solution:

3 \(\frac { 1 }{ 3 } \)+ 2 \(\frac { 1 }{ 4} \)

Let us add the whole numbers and fraction parts separately i.e.

Whole Numbers Part 3+2 = 5

Fractions Part = \(\frac { 1 }{ 3 } \)+ \(\frac { 1 }{ 4} \)

Since the denominators of the fractions are not same find the LCM of the Denominators to make them like fractions

LCM(3,4) = 12

\(\frac { 1*4 }{ 3*4 } \) + \(\frac { 1*3 }{ 4*3} \)

= \(\frac { 4 }{ 12 } \) + \(\frac { 3 }{ 12 } \)

= \(\frac { (4+3) }{ 12 } \)

= \(\frac { 7 }{ 12 } \)

Now add the like fractions and express the sum to its simplest form

= 5 \(\frac { 7 }{ 12 } \)

Therefore, 3 \(\frac { 1 }{ 3 } \), 2 \(\frac { 1 }{ 4} \) when added gives 5 \(\frac { 7 }{ 12 } \)

2. Add 5 \(\frac { 1 }{ 4} \), 2 \(\frac { 1 }{ 5} \), \(\frac { 1 }{ 6 } \)?

Solution:

5 \(\frac { 1 }{ 4} \) + 2 \(\frac { 1 }{ 5} \) + \(\frac { 1 }{ 6 } \)

Firstly, let us add the whole numbers and fraction parts separately i.e.

Whole Numbers Part (5+2+0) = 7

Fractions Part = \(\frac { 1 }{ 4} \) + \(\frac { 1 }{ 5} \) + \(\frac { 1 }{ 6 } \)

Since the Denominators of Fractions aren’t the same find the LCM of Denominators and express them as like fractions

LCM(4, 5, 6) = 60

= \(\frac { (1*15) }{ (4*15) } \) + \(\frac { (1*12) }{ (5*12)} \) + \(\frac { (1*10) }{ (6*10) } \)

= \(\frac { 15 }{ (60) } \) + \(\frac { 12 }{ 60} \) + \(\frac { 10 }{ 60 } \)

= \(\frac { (15+12+10) }{ 60 } \)

= \(\frac { 37 }{ 60 } \)

Now add the like fractions and express the sum to its simplest form

= 7 \(\frac { 37 }{ 60 } \)

Therefore, 5 \(\frac { 1 }{ 4} \), 2 \(\frac { 1 }{ 5} \), \(\frac { 1 }{ 6 } \) when added gives 7 \(\frac { 37 }{ 60 } \)

Adding Mixed Fractions Examples using Method 2

1. Add 5 \(\frac { 1 }{ 4 } \), 3 \(\frac { 1 }{ 2 } \)?

Solution:

5 \(\frac { 1 }{ 4 } \) + 3 \(\frac { 1 }{ 2 } \)

Change the given Mixed Numbers to Improper Fractions

= \(\frac { (5*4+1) }{ 4 } \) +  \(\frac { (3*2+1) }{ 2 } \)

= \(\frac { 21 }{ 4 } \) +  \(\frac { 7 }{ 2 } \)

Since the Denominators aren’t same find the LCM and express them as Like Fractions

LCM(4,2) = 2

= \(\frac { (21*1) }{ 4*1 } \) +  \(\frac { (7*2) }{ (2*2) } \)

= \(\frac { 21 }{ 4 } \) +  \(\frac { 14 }{ 4 } \)

= \(\frac { (21+14) }{ 4 } \)

= \(\frac { 35 }{ 4 } \)

Thus, 5 \(\frac { 1 }{ 4 } \), 3 \(\frac { 1 }{ 2 } \) added results in \(\frac { 35 }{ 4 } \)

2. Add 6 \(\frac { 1 }{ 4 } \), 7 \(\frac { 1 }{ 4 } \), 3 \(\frac { 1 }{ 4 } \)?

Solution:

6 \(\frac { 1 }{ 4 } \) + 7 \(\frac { 1 }{ 4 } \) + 3 \(\frac { 1 }{ 4 } \)

Change the given Mixed Fractions to Improper Fractions

= \(\frac { (6*4+1) }{ 4 } \) +  \(\frac { (7*4+1) }{ 4 } \) + \(\frac { (3*4+1) }{ 4 } \)

= \(\frac { 25 }{ 4 } \) + \(\frac {29 }{ 4 } \) + \(\frac { 13 }{ 4 } \)

= \(\frac { (25+29+13) }{ 4 } \)

= \(\frac { 67 }{ 4 } \)

Thus, 6 \(\frac { 1 }{ 4 } \), 7 \(\frac { 1 }{ 4 } \), 3 \(\frac { 1 }{ 4 } \) results in \(\frac { 67 }{ 4 } \)

FAQs on Adding Mixed Fractions

1. What is a Mixed Fraction with Example?

A Mixed Fraction is a form of a fraction that has a whole number next to a fraction. For Example 6 \(\frac { 1 }{ 4 } \) is a Mixed Fraction where 6 is a whole number and \(\frac { 1 }{ 4 } \) is the fraction part.

2. What does a Mixed Fraction look like?

Mixed Fraction is simply an improper fraction written as the sum of a whole number and a proper fraction. For instance, improper fraction \(\frac { 5 }{ 2 } \) can be written as Mixed Fraction 2 \(\frac { 1 }{ 2 } \).

3. How to add Mixed Fractions Step by Step?

Follow the simple and easy steps listed below to add Mixed Fractions and they are as such

• Convert the given Mixed Fractions to Improper Fractions
• Find the LCM of Denominators and then make them like fractions.
• Add the Like Fractions and Express the Sum to its Simplest Form.

The perimeter is the distance around a shape. A quadrilateral is a polygon that has four sides and four angles. To find the perimeter of a quadrilateral adds the measurements of four sides of it. We have given the most common types of quadrilaterals along with the perimeter of that quadrilateral. Check out the complete article and know how to find the perimeter of the quadrilateral. Some of the examples of a quadrilateral are Parallelogram, Rectangle, Square, Rhombus, and Trapezium, etc.

Also, Read:

• Sum of Angles of a Quadrilateral
• Different Types of Quadrilaterals
• Construct Different Types of Quadrilaterals

Perimeter of Different Types of Quadrilaterals

The sum of the four angles of the quadrilateral is equal to 360°. We have different types of quadrilateral. They are

1. Parallelogram
2. Rectangle
3. Square
4. Rhombus
5. Trapezium

The perimeter of the Quadrilateral is the sum of the distance around the image. That means the perimeter of a quadrilateral is equal to the sum of the four sides of the image or object. That is,

(AB + BD + DC + CA) = Perimeter of the Quadrilateral.

1. Parallelogram

Here, the lengths of the two sides of the parallelogram are equal and the breadths of the two sides of the parallelogram are equal. Opposite sides are equal in a parallelogram.
Perimeter of the Parallelogram = (AB + BD + DC + CA)
= (b + l + b + l).
Perimeter of the Parallelogram = 2(l + b).
Here, ‘l’ represents the length and ‘b’ represents the breadth of the parallelogram.
Area of the parallelogram = Base * height.

2. Rectangle

In a rectangle, both the lengths of the sides are equal and the breadths of the sides of a rectangle are equal. That means, opposite sides of the rectangle are equal.
Perimeter of the rectangle = (AB + BD + DC + CA) = (b + l + b + l) = 2(l + b).
Perimeter of the Rectangle = 2(l + b).
Area of the Rectangle = length * breadth = l *b.
Here, ‘l’ indicates the length of the rectangle and ‘b’ indicates the breadth of the rectangle.

3. Square

In this, a square is also enclosed with the four sides and the lengths of these four sides are equal.
Here, ‘a’ indicates the length of the sides of the square.
Perimeter of the square = (AB + BD + DC + CA) = (a + a + a + a) = 4a.
The perimeter of the square = 4a.
Area of the Square = Side * Side = a * a = a^2.

4. Rhombus

The lengths of the four sides of the rhombus are equal. Here, ‘a’ represents the length of the side.
Perimeter of the Rhombus = (AB + BC + CD + DA) = (a + a + a + a) = 4a.
The perimeter of the Rhombus = 4a.
Area of the Rhombus = (Base * height).

5. Trapezium

Two opposite sides of the trapezium are parallel. Perimeter of the Trapezium = (AB + BC + CD + DA).
AB + BC + CD + DA = (c + b + d + a)cm.
Area of the Trapezium = (a + b) / 2 * h.
Here, a, b, c, d are the sides of the trapezium. And ‘h’ indicates the height of the trapezium.

Perimeter of Quadrilateral Examples

1. Find the Perimeter of the Quadrilateral with the sides 2cm, 10cm, 5cm, and 20cm?

Solution:
The given information is the length of the four sides of the quadrilateral is = 2cm, 10cm, 5cm, 20cm.
The perimeter of the quadrilateral = sum of the length of the four sides of the quadrilateral.
Perimeter of the quadrilateral = (2 + 10 + 5 + 20)cm. = 37cm.

So, the perimeter of the quadrilateral is equal to 37cm.

2. The Perimeter of the quadrilateral is 40cm and the length of the three sides of the quadrilateral is 5cm, 10cm, and 5cm. Find the length of the four sides of the quadrilateral?

Solution:
The given details are the Perimeter of the quadrilateral = 40cm.
Length of the three sides of quadrilateral = 5cm, 10cm, and 5cm.
The perimeter of the quadrilateral = sum of the length of four sides of the quadrilateral.
40cm = (5 + 10 + 5 + x) cm.
40 = 20 + x.
x = 40 – 20 = 20cm.

Finally, the length of the fourth side of the quadrilateral is equal to 20cm.

3. A woman crosses a distance of 24m long while going round a quadrilateral field twice. What will be the cost of fencing the field at the rate of cost $1.20per m?

Solution:
The given information is Women crosses a distance of 24m long = perimeter of its boundary = 24 / 2 = 12m.
Cost of fencing the field for 1m = $1.20.
Then the cost of 12m of fencing the field = 12 * $1.20 = $14.4.

Therefore, the cost of the 12m fencing field is equal to $14.4.

4. One side of the square is 4cm. Find the perimeter of the square?

Solution:
As per the given information, the length of the side of the square = 4cm.
The perimeter of the square = 4a.
Here, a = 4.
By substituting the ‘a’ value in the formulae, we will get
Perimeter of the square = 4 * 4 = 16cm.

So, the perimeter of the square is equal to 16cm.

5. Length of the rectangle is 10cm and the breadth of the rectangle is 5cm. Calculate the Perimeter of the Rectangle?

Solution:
As per the given details, the Length of the rectangle (l) = 10cm.
Breadth of the rectangle (b) = 5cm.
Perimeter of the rectangle = 2(l + b).
By substituting the values in the formulae, we will get like
Perimeter of the rectangle = 2(10 + 5) = 2(15) = 30cm.

Therefore, the perimeter of the rectangle is equal to 30cm.

6. If the area of the rhombus is 20 square units and the height of the rhombus is 6 units, then calculate the base of the rhombus?

Solution:
From the given information, Area of the Rhombus = 20 Sq units.
Height of the Rhombus (h) = 6 units.
Area of the Rhombus = Base * height.
20 = Base * 6.
Base = 20 / 6 = 10 / 3 = 0.3 units.

The base of the Rhombus is equal to 0.3 units.

Frequently Asked Questions

1. What is Quadrilateral?

The quadrilateral is enclosed with four sides. It has four corners, four angles, and four sides. The total angle of the quadrilateral is equal to 360°.

2. What are the types of Quadrilateral?

The types of Quadrilateral are,
1. Square
2. Rectangle
3. Parallelogram
4. Trapezium
5. Rhombus

3. How we can find the perimeter of a quadrilateral?

The area of the quadrilateral is the sum of all sides of the quadrilateral. Yes, by adding all sides of the quadrilateral, we can find the perimeter of the quadrilateral.