Common Core Math

Practice Test on Ratio and Proportion helps students to get knowledge on different levels. The Ratio and Proportion Questions and Answers provided range from beginner, medium, hard levels. Practice the Questions here and get to know how to solve different problems asked. All the Ratio and Proportion Word Problems covered are as per the latest syllabus. Master the topic of Ratio and Proportion by practicing the Problems on a consistent basis and score better grades in your exam.

Ratio and Proportion Questions and Answers

1. The ratio of monthly income to the savings in a family is 5 : 3 If the savings be $6000, find the income and the expenses?

Solution:

Let us assume the Income be 5x

whereas savings be 3x

Given Savings = $6000

3x = 6000

x = 6000/3

= 2000

Income = 5x

= 5*2000

= $10,000

Expenses = Income – Savings

= 5x – 3x

= 2x

= 2*2000

= $4000

Therefore, Income and Expenses are $10,000 and $ 4000.

2. Two numbers are in the ratio 7: 4. If 3 is subtracted from each of them, the ratio becomes 5 : 2. Find the numbers?

Solution:

Let us consider the number be x

so 7x:4x

If 3 is subtracted the ratio becomes 5:2 then we have

7x-3:4x-3 = 5:2

equating them ad solving we get the values as

7x-3/4x-3 = 5/2

(7x-3)2 = 5(4x-3)

14x-6 = 20x-15

-6+15 = 20x-14x

9 = 6x

6x = 9

x = 9/6

= 3/2

Therefore the numbers are 7(3/2) and 4(3/2)

= 21/2, 6

3. Two numbers are in the ratio 3 : 5. If their sum is 720, find the numbers?

Solution:

Let us consider the number be x

Therefore two numbers become 3x:5x

Since their Sum = 720

3x+5x = 720

8x = 720

x = 720/8

= 90

Numbers are 3x and 4x

Thus, they become 3(90) and 4(90) i.e. 270 and 360.

4. A sum of money is divided among Rohan and Anand in the ratio 4 : 6. If Anand’s share is $600, find the total money?

Solution:

Let the money be x

Rohan and Anand’s Share = 4x:6x

Anand’s Share = $600

6x = $600

x = $100

Rohan’s Share = 4x

= 4*100

= $400

Total Money = Rohan’s Share + Anand’s Share

= $400+$600

= $1000

Therefore, the Sum of Money is $1000

5. The difference between the two numbers is 33 and the ratio between them is 5 : 2. Find the numbers?

Solution:

Let the number be x

From the given data

we have 5x-2x = 33

3x = 33

x = 11

Numbers are 5x, 2x

thus, they become 5*11 and 2*11

= 55, 22

Therefore, the numbers are 55 and 22.

6.  The ages of A and B are in the ratio 3 : 6. Four years later, the sum of their ages is 53. Find their present ages?

Solution:

Let the Present Ages be 3x and 6x

After four Years Age of A and B Becomes 3x+4 and 6x+4

We know sum of their ages after 4 years = 53

3x+4+6x+4 = 53

9x+8 = 53

9x = 53-8

9x = 45

x =5

Present Ages of A and B is 3x and 6x

thus 3*5 and 6*5 i.e. 15 and 30

Therefore, the Present Ages of A and B are 15 and 30.

7. If 3A = 4B = 5C, find the ratio of A : B : C?

Solution:

Let us assume that 3A = 4B = 5C = k

Equating them we have A = k/3, B = k/4, C = k/5

Therefore, Ratio becomes = k/3:k/4:k/5

LCM of 3, 4, 5 is 60

Thus expressing them in terms of least common multiple we have

A:B:C = 20:15:12

Therefore, Ratio of A:B:C is 20:15:12

8. A certain sum of money is divided among a, b, c in the ratio 3:4:5. of a share is $300, find the share of b and c?

Solution:

Let us consider the sum of money as x

Since it is shared among the ratio of 3:4:5 we have 3x:4x:5x

We know a’s share is 3x = $300

x =$100

Share of b = 4x

= 4*100

= $400

Share of C = 5x

= 5*100

= $500

9. Divide $900 among A, B, C in the ratio 3: 4 ∶ 5?

Solution:

Let us assume the total money as x

Since the sum is to be shared among A, B, C in the ratio of 3:4:5 we have

3x+4x+5x = $900

12x = $900

x = $900/12

=$75

Share of A = 3x

= 3*75

= $225

Share of B = 4x

= 4*75

= $300

Share of C = 5x

= 5*75

= $375

10. Find the first term, if second, third, and fourth terms are 21, 80, 120?

Solution:

Let the Terms be a, a+d, a+2d, a+3d

Given Second Term = 21

a+d = 21

Third Term = 80

a+2d = 80

Fourth Term = 120

a+3d = 120

Using the Eliminating Method

a+d = 21

a+2d = 80

_______

Subtracting them we get the value of d as

-d = -59

d= 59

Substitute the value of d in any of the terms

a+d = 21

a+59 =21

a =21-59

= -38

The word problems on profit and loss are solved here to get the basic idea of how to use the formulae of profit and loss in terms of cost price and selling price. We have explained the entire concept of profit and loss and various formulae when C.P, S.P, Profit %, or Loss % is given. Solve Different Questions on Profit and Loss available here to test your grip on the fundamentals of the concept.

Profit or Gain

If the selling price of an item is more than the cost price of the same item, then it is said to be gain (or) profit i.e. S.P. > C.P.

Net profit= S.P. – C.P.

Loss

If the selling price of an item is less than the cost price of the same item, then it is said to be a loss i.e. S.P.  < C.P.

Net loss = C.P. – S.P.

Profit and Loss Word Problems with Answers

Question 1:

A laptop was brought for $ 80,000 and sold at a loss of $ 5000. Find the selling price.

Solution:

Given data:

The cost price of the laptop is $ 80,000

Loss = $ 5000

We know that,

Loss = C.P. – S.P.

$ 5000 =$ 80,000 – S.P.

S.P. = $ 80,000 – $ 5000

S.P. = $ 75,000

Therefore, the selling price of the laptop is $ 75,000.

Question 2:

Abhi sold his water purifier for $ 4000, at a loss of $ 300. Find the cost price of the water purifier.

Solution:

Given Data:

The selling price of water purifier = $ 4000

Loss = $ 300

We know that, Loss = C.P. – S.P.

From this, we can note that,

Cost price = loss + selling price

= $ 300 + $ 4000

= $ 4300

Hence, the cost price of a water purifier is $ 4300.

Question 3:

Deepika sold her gold necklace for $ 60,000 at a profit of $ 10,000. Find the cost price of the gold necklace.

Solution:

Given data

The selling price of gold necklace = $ 60,000

Gained a profit = $ 10,000

From the formula

Gain = Selling price (S.P.) – Cost price (C.P.)

We get,

Cost price (C.P.) = Selling price (S.P.) – Gain

= $ 60,000 – $ 10,000

= $ 50,000.

Hence, the cost price (C.P.) of the gold necklace is $ 50,000.

Question 4:

Karthik buys a watch for $ 6000 and sells it at a gain of 5⅓ %. For how much does he sell it?

Solution:

Given Data:

Cost price (C.P.) of watch = $ 6000

Gain = 5⅓% = 16/3 %

We know that

Gain% = ((S.P. – C.P.)/C.P. *100) %

From above,

S.P. = [{(100 + gain %) /100) * C.P.]

= $ [{(100 + 16/3)/100} * 6000]

= ${(103.33/100) * 6000]

= $ 6199.8

Hence, karthik sells his watch at an amount of $ 6199.8.

Question 5:

Siva ram bought an old bike for $ 15000 and spends $ 2000 on repairs. If he sells the bike for $ 21150, what is his gain percentage?

Solution:

Given data:

Cost price (C.P.) of bike = $ 15000

Repair cost = $ 2000

Total Cost Price = Original Price of the Bike + Repair Cost

= $ 15000+$2000

= $17000

Selling price (S.P.) of bike = $ 21150

As the selling price (S.P.) is more than the cost price (C.P.) of the bike then it is said to be in gain

Therefore, Gain = Selling price (S.P.) – Cost Price (C.P.)

= $ 21150 – $ 17000

= $ 4150.

Gain % = ((S.P. – C.P.)/C.P. *100) %

= $ (4150/17000 * 100) %

= 24. 41%

Hence, He got a 24.41% gain on his bike.

Question 6:

If the selling price of an object is doubled, the profit of the object triples. Find the profit percentage.

Solution:

Given data:

Let the cost price of the object be $ ‘a’

And selling price of the object be $ ‘b’

According to the question, the profit is tripled and selling price is doubled hence

Profit = $ 3(b – a)

Profit = S.P. – C.P.

3(b – a) = 2b –a

3b – 3a = 2b – a

Therefore, b = 2a.

Profit =$ b – a

= 2a –a

= $ a.

Profit% = ((S.P. – C.P.)/C.P. *100) %

= (a/a * 100) %

= 100%.

Question 7:

The percentage profit earned by selling an article for $ 3000 is equal to the percentage loss incurred by selling the same article for $ 2500. At what price should the article be sold to make a 20% profit?

Solution:

The above question says that the % profit earned by selling the article is equal to the % loss incurred

by the same article.

Given data:

Let the C.P. of the article be ‘P’

We know that

Profit % = ((S.P. – C.P.)/C.P. *100) %

And loss % = ((C.P. – S.P.)/C.P. *100) %

((3000 – p)/p * 100) = ((p – 2500)/p * 100)

2p = 7500

P = $ 3750.

Calculating selling price at a profit of 20%

Profit % = ((S.P. – C.P.)/C.P. *100) %

From above,

S.P. = $ [{(100 + gain %) /100) * C.P.]

= $ ((100 + 20)/100) * 3750)

= $ 4500.

Question 8.

If mangoes are bought at prices ranging from $ 300 to $ 450 are sold at prices ranging from $ 400 to $ 525, what is the greatest possible profit that might be made in selling ten mangoes?

Solution:

The question says that the mangoes are bought at a certain range and sold at a certain range. It says to find the greatest profit on selling ten mangoes.

Given data:

Cost price (C.P.) of mangoes ranging from = $ 300 – $ 450

Selling price (S.P.) of mangoes ranging from = $ 400 – $ 525

Considering,

Least cost price (C.P.) for ten mangoes = $ 300*10

= $ 3000

Greatest selling price (S.P.) of mangoes = $ 525*10

= $ 5250

Profit = S.P. – C.P.

= $ 5250 – $ 3000

= $ 2250.

Hence, the required profit obtained is $ 2250 on selling mangoes.

Question 9:

On selling 18 toys at $ 800, there is a loss equal to the cost price of 7 toys. The cost price of the toys is?

Solution:

Given data:

Let the cost price (C.P.) of the toys be ‘m’

Given, on selling 18 toys at $ 800, there is a loss equal to the cost price of 7 toys

According to the question, the equation is written as:

18m – 800 = 7m

Solving the above equation

We get m = $ 32

Therefore, the cost price of the toy is $ 32.

Before, going for examples on simplification, know the rules and methods. Check all the best possible methods to solve the simplification of expressions. Refer to all the formulae, rules, and methods for the simplification of integers. You can go through the entire article to know more on what are the rules to be followed while simplifying expressions. Practice the Simplification Questions available and cross-check your answers here to know where you stand in your preparation level.

Rules of Simplification

While solving the Examples on Simplification keep the below pointers in mind. They are as follows

1. Remove Brackets – If two or more signs occur in the expression, then convert them into one. The brackets will be square, round and curly braces.
2. Group the values into one group i.e., either positive or negative.
3. Whenever there are two integers, the result will give the sign of the greater value.

Examples on Simplification

Question 1.

At 135 feet below sea level, a submarine has started. It dives 239 feet before rising 307 feet. Find the exact depth of the submarine at which it is spent currently?

Solution:

As per the given question,

At 135 feet below sea level, a submarine has started

The level at which it dives = 239 feet

The rise of the sea level =307 feet

To find, the current depth of the submarine, we write the equation as

-135+(-239)+307

=-374+307

=-67

Therefore, the current depth of the submarine is 67 feet below sea level.

The final solution is -67 feet.

Question 2:

Jenny purchases a credit card from a local retailer. She begins with a $200 balance. She then makes the following purchases: lamp $8, rug $63, vacuum $39. After this shopping trip, she loads $147 on her card, then spends $113 on groceries. Express each transaction as an integer, then determine the new balance on the prepaid credit card?

Solution:

As per the given question,

Jenny begins with a balance = $200

She purchases lamp = $8

She purchases rug = $63

She purchases vacuum = $39

She loads on her card = $133

As she has the balance of $200, it is positive, and also she loads $147 to her card, therefore it is also positive. The remaining values are negative.

The new balance on the prepaid credit card = 200 +(-8) + (-63) + (-39) + 147 + (-113)

= 347 + (-223)

=124

Therefore, the new balance on the prepaid credit card = $124

Hence, the final solution = $124

Question 3:

Simplify: 37 – [5 + {28 – (19 – 7)}]

Solution:

Step 1: Innermost grouping symbols removal is the first step to simplify the expression. Consider {28-(19-7)}, to remove the brackets we subtract the equation {28-(19-7)}, here comes as {28-12}
The simplified expression is 37 – [5 + {28 – 12}]
Step 2: Follow the same procedure to remove parentheses in {28-12}, we have to subtract the equation {28-12}, here comes the final equation as
37 – [5 + 16]
Step 3: Now, the equation is further simplified and it contains only square brackets, we should perform all the set of operations within two brackets.
37 – 21
Step 4: In the final step, we subtract the values and the final result will be 16.
Thus the final solution will be 16.

Question 4:

Simplify the equation 15 – (-5) {4 – 7 – 3} ÷ [3{5 + (-3) x (-6)}]

Solution:

Step 1: Innermost grouping symbols removal is the first step to simplify the expression. Consider {5+(-3)x(-6)}, to remove the brackets we multiply the equation {5+18}, here comes the final expression as

15 – (-5) {4 – 7 – 3} ÷[3 {5 + 18}]

Step 2: Follow the same procedure to remove parentheses in {4-7-3}, we have multiplied the equation {4-7-3}, here comes the final result as 4-4

After performing 2 steps, the result equation will be

15 – (-5) x 0 ÷[3 {5 + 18}]

Step 3: Next simplification must be the addition of 5 and 18. The result will be

15 – (-5) x 0 ÷ 3 x 23

Step 4: As the brackets of two sets are removed. Therefore, change the negative signs and rewrite the equation.

15 + (5 x 0) ÷ 3 x 23

Step 5: As all other brackets are removed and the expression contains only and braces. Perform all the operations that are possible within the brackets.

= 15 – (-5) x 0 ÷ 69

Step 6: On further simplification, the result will be

15 – (-5) x 0

Step 7:

Therefore, the final solution is 15

Question 5:

The temperature of the fridge compartment is set at 8 degrees C. The freezer compartment is set at -10 degrees C. What is the difference between the temperature settings?

Solution:

As per the given question,

The temperature of fridge compartment = 8 degrees C

Temperature of freezer compartment = -10 degree C

Difference between temperature = 8-(-10)

=8+10

=18 degrees C

Question 6:

Rekha climbs up 5 stairs every second and then climbs down 2 stairs over the next second. How many seconds will she take to climb 60 steps?

Solution:

As per the given question,

Stairs climbed up by Rekha = 5 in 1 sec

Stairs climbed down by Rekha = 2 in 1 sec

Climbing down is considered as a decrease in value, hence it is negative.

Therefore, stairs climbed = 5+(-2) in 2 secs

Steps climbed = 3 stairs in 2 secs

Thus, the time to climb 1 step in time = 2/3 secs

Thus, the time taken to climb 60 steps = 2 x 60/3

= 40sec

Hence, the final solution is 40 sec.

Question 7:

I start with integer (-8), Add (-12) to it, subtract 10 from the result. Divide the result by (+3) and multiply the answer by (-2). What do you get?

Solution:

Step 1: As given in the question, the integer value is -8

Step 2: Adding -12 to the integer value

i.e., -8-12=-20

Step 3: Subtracting 10 from the value = -20-(10) = -30

Step 4: Dividing by +3

=(-30)/(3) = -10

Step 5: Multiply the answer by -2

(-10) x (-2) = 20

Therefore, the final solution is 20

Question 8:

Arnav has $20. He spent $8 on Monday. He got $5 as pocket money on Tuesday. He gave a $7 loan to his friend on Wednesday. He ate ice cream for $10 on Thursday. He received a reward of $5 on Friday. He repaid the loan of $7 on Saturday. How much money did Arnav totally have on Sunday?

Solution:

As per the given question,

Arnav has $20

He spent on Monday = $8

He got pocket money on Tuesday = $5

He gave a loan to a friend on Wednesday = $7

He ate ice cream on Thursday = $10

Received a reward on Friday = $5

His friend repay the loan on Saturday = $7

Money Arnav has on Sunday = 20+(-8)+5(-7)+(-10)+5+7

=20+5+5+7+(-8)+(-7)+(-10)

=37-8-7-10

=37-25

=12

Therefore, the money Arnav has on Sunday = $12

Question 9:

A Hiker is descending 152m in 8 minutes. What will be his elevation in half an hour?

Solution:

As given in the question,

In 8 mins Hiker descends 152cm.

In 1 min Hiker descends = 152/8 = 19m

Therefore, In 30min Hiker descends = 19 x 30 = 570m

Hence, the final solution is 570m

Question 10:

In an exam, the student gets +4 for each correct answer and -2 for each wrong answer. Rohith’s final score is 68 marks and he attempted 25 questions correctly. How many marks did he lose for wrong answers?

Solution:

Rohith’s final score = 68 marks

Rohith attempted correctly = 25 questions

Let the number of wrong answers be a

Marks for correct answers = 25 x 4 = 100

Marks for wrong answers = a x (-2) = -2a

Total wrong answers = 100 +(-2a) = 68

100-2a=68

-2a=68-100

-2a=-32

a=32/2

a=16

Therefore, Rohith lost 16 marks for wrong answers.

Removal of brackets involves step by step process. We are providing a detailed procedure and various rules to follow while removing the brackets. Also, check the various methods to remove different types of brackets. Rewrite the expression by simplifying it with the help of the brackets removal function. Know the process of writing in equivalent forms by removing the brackets. Refer to the definitions of “expanding” or “removing” brackets.

How to Remove Brackets from an Equation?

There are various steps involved in bracket removal. In the further sections, we will see how the equations can be written in equivalent forms by removing the braces. This process is called “removing” or “expanding” brackets.

The actual procedure to remove the brackets is to multiply the term which is outside the brackets with the term which is inside the brackets. This is also called the law of distribution.

Steps to Brackets Removal

In Order to take off brackets, you need to follow the step by step guidelines listed below and they are as follows

Step 1:

Check for the given question or the expression whether it contains a vinculum(The horizontal line which is used in the mathematical notation for the desired purpose) or not. If there is a vinculum, then perform the operations in it. Or else go to step 2

Step 2:

Now, go for the equation and check for the innermost bracket and then perform the operation within that bracket.

Step 3:

To perform step 3, there are various rules to be followed.

Rule 1: If the equation is preceded by addition or plus sign, then remove it by writing the terms as mentioned in the equation.

Rule 2: If the equation is preceded by a negative or minus sign, then change the negative signs within it to positive or vice versa.

Rule 3: The indication of multiplication is there will be no sign between a grouping symbol and a number.

Rule 4: If there is any number before the brackets, then we multiply that number inside the brackets with the number which is outside the brackets.

Step 4:

Check for the next innermost bracket and perform the calculations or operations within it. Remove the next innermost bracket by using Step III rules. Follow this process until all the brackets are removed.

Removing Brackets by FOIL Method

Brackets can be easily removed and rules can be remembered by using the FOIL Method. Whenever multiplication is necessary outside the brackets, multiply each of the terms in the first bracket by each of the terms in the second bracket.

To avoid confusion, we apply the FOIL Method and make the calculations simple further.

In FOIL, F indicates First, O indicates Outside, I indicates Inside, L indicates Last

First: Multiply the initial terms of each bracket i.e., the first term of the first bracket with the first term in the second bracket.

Outside: Outside indicates multiplying the 2 outside terms i.e., the first term in the first bracket with the second term in the second bracket.

Inside: Multiplication of 2 inside terms inside Inside in FOIL Method i.e., the second term in the first bracket with the first term in the second bracket.

Last: Last indicates multiplication of last terms from both the brackets i.e., the second term in the first bracket with the second term in the second bracket.

Example:

(x+5)(x+10)

= (x+5)x + (x+5)10

x²+ 5x + 10x + 50

= x²+15x + 50

Removing Brackets Questions

Consider an algebraic expression which contains parentheses or round brackets ( ), square brackets [ ], curly brackets { }.

5{[4(y-4)+15] – [2(5y-3)+1]}

Step 1:

Innermost grouping symbols removal is the first step to simplify the expression. Consider (y-4), to remove the brackets we multiply the equation (y-4) by 4, here comes as 4y-16.

Step 2:

Follow the same procedure to remove parentheses in 2(5y-3), we have multiplied the equation (5y-3) by 2, here comes the final equation as 10y-6

After performing 2 steps, the result equation will be

5{[4y-16+15] – [10y-6+1]}

Step 3:

Now, the equation is further simplified and it contains only square brackets and curly brackets, we should perform all the set of operations within two brackets.

5{[4y-16+15] – [10y-6+1]}

=5{[4y-1]-[10y-5]}

Step 4:

As the brackets of two sets are removed. Therefore, the negative sign before the 2nd set implies for all the terms present in the 2nd set. Therefore, it is multiplied by -1

5{[4y-1]-[10y-5]}

=5{4y-1-10y+5}

Step 5:

As all other brackets are removed and the expression contains only curly braces. Perform all the operations that are possible within the brackets.

5{4y-1-10y+5}

=5{-6y+4}

Step 6:

To the open curly braces, apply the distributive law.

5{-6y+4}

=-30y+20

Example 2:

Simplify the equation 95 – [144 ÷ (12 x 12) – (-4) – {3 – 17 – 10}]

Solution:

Step 1:

Innermost grouping symbols removal is the first step to simplify the expression. Consider {3-17-10}, to remove the brackets we subtract the equation {3-17-10}, here comes as {3-7}

Step 2:

Follow the same procedure to remove parentheses in (12 x 12), we have multiplied the equation (12 x12), here comes the final equation as 144

After performing 2 steps, the result equation will be

95 – [144 ÷ 144 – (-4) – {3-7}]

Step 3: 

Now, the equation is further simplified and it contains only square brackets and curly brackets, we should perform all the set of operations within two brackets.

95 – [1 – (-4) – (-4)]

Step 4:

As the brackets of two sets are removed. Therefore, change the negative signs and rewrite the equation.

= 95 – [1 + 4 + 4]

Step 5:

As all other brackets are removed and the expression contains only square braces. Perform all the operations that are possible within the brackets.

= 95 – 9

Step 6:

Therefore, after subtraction the final solution is

=86

Example 3:

Simplify the equation 197 – [1/9{42 + (56 – 8 + 9)} +108]

Solution:

Step 1:

Innermost grouping symbols removal is the first step to simplify the expression. Consider {56-8+9}, to remove the brackets we subtract the equation {56-8+9}, here comes as {56-17}

= 197 – [1/9 {42 + (56 – 17)} + 108]

Step 2:

Follow the same procedure to remove parentheses in {42 + (56 – 17)}, we have subtracted the equation (56-17), here comes the final equation as {42 + 39}

After performing 2 steps, the result equation will be

197 – [1/9 {42 + 39} + 108]

Step 3:

Now, the equation is further simplified and it contains only square brackets and round brackets, we should perform all the set of operations within two brackets.

197 – [(81/9) + 108]

Step 4:

Now, simplify the equation (81/9), then the result will be 9. The final equation will be

197 – [9 + 108]

Step 5:

As all other brackets are removed and the expression contains only square braces. Perform all the operations that are possible within the brackets.

= 197 – 117

Step 6:

To get the final result, subtract 117 from 197, therefore the final result will be 80

How to Expand Brackets?

There are few different methods to expand brackets and simplify expressions. We have explained each of them in detail and even took expanding brackets examples for explaining the entire process. They are as such

1. Multiplying two bracketed terms together

If we have a situation to multiply two bracketed terms, then we multiply each term in the first bracket with each term in the second bracket. These types of multiplications lead to quadratic expressions.

Example:

(x+5)(x+10)

=(x+5)x + (x+5)10

2. Dealing with nested brackets

These are the collection of expressions nested in various sets of brackets.

Example:

Simplify -{5x-(11y-3x)-[5y-(3x-6y)]}

-[5x-(11y-3x)-[5y-3x+6y]}

-{5x-11y+3x-5y+3x-6y}

-{11x-22y}

-11x+22y

Do you want to know How to construct different types of quadrilaterals? Different types of quadrilaterals are developed depending on the sides, diagonals, and also angles. Have a look at a step by step explanation to construct various types of quadrilaterals. We have given different problems on the construction of quadrilaterals along with steps for better understanding. Look at them and practice all the problems given below and enhance your conceptual knowledge.

How to Construct Quadrilaterals? | Steps of Construction

You can refer to the below available various questions on constructing quadrilaterals along with a detailed explanation. For the sake of your comfort, we even jotted Steps of Construction for each and every problem so that you can solve similar kinds of questions easily.

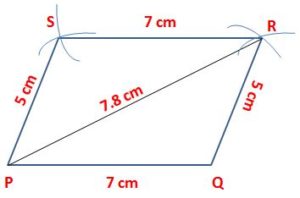
1. Construct a parallelogram PQRS in which PQ = 7 cm, QR = 5 cm and diagonal PR = 7.8 cm.

Steps of Construction:
Firstly, draw a rough figure of the quadrilateral with the given dimensions.

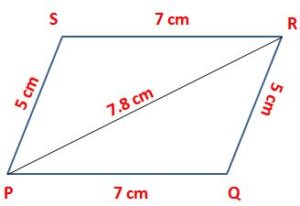
1. Draw a line segment of length 7 cm and mark the ends as P and Q.
2. Take the point P as a center and draw an arc by taking the radius 7.8 cm.
3. Next, take point Q as a center and draw an arc by taking the radius 5 cm. Mark the point as R where the two arcs cross each other. Join the points Q and R as well as P and R.
Note: A parallelogram is a simple quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure.
4. By taking the point P as a center, draw an arc with a radius of 5 cm.
5. By taking the point R as a center, draw an arc with a radius of 7 cm.
6. Mark the point as S where the two arcs cross each other. Join the points R and S as well as P and S.

PQRS is a required parallelogram.

2. Construct a parallelogram, one of whose sides is 7.2 cm and whose diagonals are 8 cm and 8.4 cm.

Steps of Construction:
Firstly, draw a rough figure of the quadrilateral with the given dimensions.

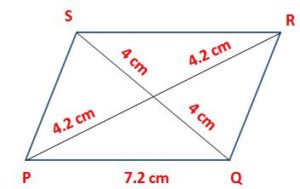
1. Draw a line segment of length 7.2 cm and mark the ends as P and Q.
2. Take the point P as a center and draw an arc by taking the radius 4.2 cm.
3. Next, take point Q as a center and draw an arc by taking the radius 4 cm. Mark the point as O where the two arcs cross each other. Join the points Q and O as well as P and O.
4. By taking the point O as a center, draw an arc with the required radius.
5. Produce PO to R such that OR = PO and produce QO to S such that OS = OQ.
6. Join PS, QR, and RS.

PQRS is a required parallelogram.

3. Construct a parallelogram whose diagonals are 5.6 cm and 6.4 cm and an angle between them is 70°.

Steps of Construction:
1. Draw a line segment of length 5.6 cm and mark the ends as P and R.
2. Take the point O as a center in between P and R.
3. Next, take point O as a center and make a point by taking 70º using a protector. Draw a line XO to Y.
4. Set off OQ = 1/2 (6.4) = 3.2 cm and OS = 1/2 (6.4) =3.2 cm as shown.
5. Join PQ, QR, RS, and SP.

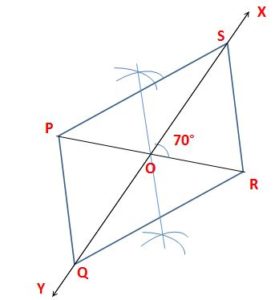
PQRS is a required parallelogram.

4. Construct a rectangle PQRS in which side QR = 5.2 cm and diagonal QS = 6.4 cm.

Steps of Construction:
Firstly, draw a rough figure of the quadrilateral with the given dimensions.

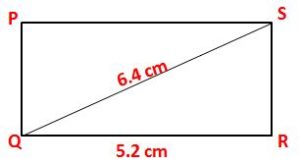
1. Draw a line segment of length 5.2 cm and mark the ends as Q and R.
2. Take the point R as a center and draw a perpendicular line to QR.
3. Next, take point Q as a center and draw an arc by taking the radius 6.4 cm. Mark the point as S where the line and arc cross each other. Join the points Q and S as well as R and S.
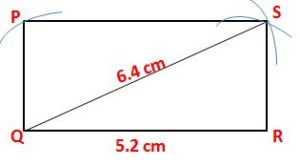
4. By taking the point S as a center, draw an arc with the required radius of 5.2 cm.
5. Take the point Q as a center and draw a perpendicular line to QR. Mark the point as P where the point and arc cross each other. Join the points Q and P as well as P and S.

PQRS is a required rectangle.

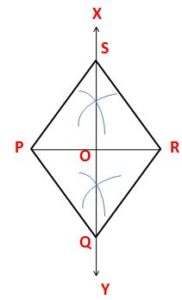
5. Construct a square PQRS, each of whose diagonals is 5.4 cm.

Steps of Construction:
1. Draw a line segment of length 5.4 cm and mark the ends as P and R.
2. Draw the right bisector XY of PR, meeting PR at O.
3. From O set off OQ = 1/2 (5.4) = 2.7 cm along OQ and OS = 2.7 cm along OX.
4. Join PQ, QR, RS, and SP.

PQRS is a required square.

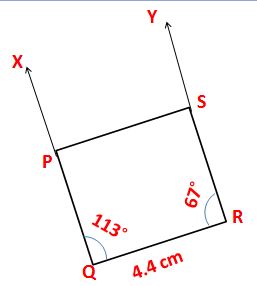
6. Construct a rhombus with a side of 4.4 cm and one of its angles equal to 67°.

Steps of Construction:
Given that a rhombus with a side of 4.4 cm and one of its angles equal to 67°.
The adjacent angle = (180° – 67°) = 113°.
1. Draw a line segment of length 4.4 cm and mark the ends as Q and R.
2. Make ∠RQX = 113° and ∠QRY = 67°.
3. Set off QP = 4.4 cm along with QX and RS = 4.4 cm along with RY.
4. Join PS.

PQRS is a required rhombus.

Different Geometry shapes and objects are named based on the number of sides. If an object has three sides, then it is classified as Triangle, An object with 4 sides classified as Quadrilateral, etc. Let us learn about the Quadrilateral definition, types, formula, properties, etc. in detail in this article. Every concept is explained separately on our website. Access every topic and easily get a grip on the Quadrilateral concept.

List of Quadrilateral Concepts

Find different concepts of Quadrilateral by checking out the below links. All you need is simply tap on them to have an idea of the related concept.

• What is a Quadrilateral?
• Different Types of Quadrilaterals
• Construction of Quadrilaterals
• Construct Different Types of Quadrilaterals

Quadrilateral Definition

A quadrilateral defined as a figure that has four sides or edges. Also, the quadrilateral consists of four vertices. rectangle, square, trapezoid, and kite, etc. are some of the examples of Quadrilateral.

Types of Quadrilaterals

There are various types of Quadrilaterals available. All the Quadrilaterals must have 4 sides. Also, the sum of the angles of the Quadrilateral is 360 degrees.

1. Trapezium
2. Kite
3. Parallelogram
4. Rectangle
5. Squares
6. Rhombus

Also, the quadrilaterals are classified differently. They are
Convex Quadrilaterals: It is defined as both diagonals of a quadrilateral are always present within a figure.
Concave Quadrilaterals: Concave Quadrilaterals one diagonals present outside of the figure.
Intersecting Quadrilaterals: The pair of non-adjacent sides intersect in Intersecting Quadrilaterals. These are also called self-intersecting or crossed quadrilaterals.

Quadrilateral Formula

Check out the below formula of a Quadrilateral.

Area of a Parallelogram = Base x Height
Area of a Square = Side x Side
Area of a Rectangle = Length x Width
Area of a Kite = 1/2 x Diagonal 1 x Diagonal 2
Area of a Rhombus = (1/2) x Diagonal 1 x Diagonal 2

Quadrilateral Properties

Know the different properties of a Quadrilateral PQRS.

• Four sides: PQ, QR, RS, and SP
• ∠P and ∠Q are adjacent angles
• Four vertices: Points P, Q, R, and S.
• PQ and QR are the adjacent sides
• Four angles: ∠PQR, ∠QRS, ∠RSP, and ∠SPQ.
• ∠P and ∠R are the opposite angles
• PQ and RS are the opposite sides

Important Properties of Quadrilateral

• Every quadrilateral consists of 4 sides, 4 angles, and 4 vertices.
• Also, the total of interior angles = 360 degrees

Properties of a Square

• The sides of a square are parallel to each other.
• Also, all the sides are equal in measure.
• The diagonals of a square perpendicular bisect each other.
• All the interior angles of a square are at 90 degrees.

Rectangle Properties

• The diagonals of a rectangle bisect each other.
• The opposite sides consist of equal length in a rectangle.
• All the interior angles of a rectangle are at 90 degrees.
• The opposite sides are parallel to each other

Properties of a Rhombus

• By adding two adjacent angles of a rhombus we get 180 degrees.
• The opposite sides are parallel to each other in a rhombus.
• The diagonals perpendicularly bisect each other
• All four sides of a rhombus are of equal measure.
• The opposite angles are of the same measure.

Parallelogram Properties

• The opposite angles of a parallelogram are of equal measure.
• The opposite side is of the same length in a parallelogram.
• The sum of two adjacent angles of a parallelogram is equal to 180 degrees.
• The opposite sides are parallel to each other in a Parallelogram.
• The diagonals of a parallelogram bisect each other.

Trapezium Properties

• The two adjacent sides are supplementary in a trapezium.
• Only one pair of the opposite side is parallel to each other in a trapezium.
• The diagonals of a trapezium bisect each other in the same ratio

Kite Properties

• The large diagonal bisects the small diagonal of a kite.
• The pair of adjacent sides have the same length in a kite.
• Only one pair of opposite angles are of the same measure.

Notes on Quadrilateral

• A quadrilateral is a parallelogram is 2 pairs of sides are parallel to each other.
• Also, a quadrilateral is a trapezoid or a trapezium if two of its sides are parallel to each other.
• A quadrilateral is a rhombus if all the sides are of equal length and the two pairs of sides are parallel to each other.
• The quadrilateral becomes kite when 2 pairs of adjacent sides are equal to each other.
• Quadrilateral becomes Square and Rectangle when all internal angles are right angles, all angles are right angles, and also the opposite sides of a rectangle are same.
• Furthermore, the Quadrilateral becomes Square and Rectangle when Opposite sides of a rectangle and square are parallel. The sides of a square are of the same length.

Ratio and Proportion are mainly explained using fractions. If a fraction is expressed in the form of a:b it is called a ratio and when two ratios are equal it is said to be in proportion. Ratio and Proportion is the fundamental concept to understand various concepts in maths. We will come across this concept in our day to day lives while dealing with money or while cooking any dish. Check out Definitions, Formulas for Ratio and Proportion, and Example Questions belonging to the concept in the further modules.

Quick Links of Ratio and Proportion Topics

If you want to get a good hold of the concept Ratio and Proportion you can practice using the quick links available for various topics in it. You just need to tap on the direct links available and get a good grip on the concept.

• Practice Test on Ratio and Proportion
• Worked out Problems on Ratio and Proportion

What is Ratio and Proportion?

Ratio and Proportion is a crucial topic in mathematics. Find Definitions related to Ratio and Proportion along with examples here.

In Certain Situations comparison of two quantities by the division method is efficient. Comparison or Simplified form of two similar quantities is called ratio. The relation determines how many times one quantity is equal to the other quantity. In other words, the ratio is the number that can be used to express one quantity as a fraction of other ones.

Points to remember regarding Ratios

• Ratio exists between quantities of a similar kind
• During Comparison units of two things must be similar.
• There should be significant order of terms
• Comparison of two ratios is performed if the ratios are equivalent similar to fractions.

Proportion – Definition

Proportion is an equation that defines two given ratios are equivalent to each other. In Simple words, Proportion states the equality of two fractions or ratios. If two sets of given numbers are either increasing or decreasing in the same ratio then they are said to be directly proportional to each other.

Ex: For instance, a train travels at a speed of 100 km/hr and the other train travels at a speed of 500km/5 hrs the both are said to be in proportion since their ratios are equal

100 km/hr = 500 km/5 hrs

Continued Proportion

Consider two ratios a:b and c:d then in order to find the continued proportion of two given ratio terms we need to convert to a single term/number.

For the given ratio, the LCM of b & c will be bc.

Thus, multiplying the first ratio by c and the second ratio by b, we have

The first ratio becomes ca: bc

The second ratio becomes bc: bd

Thus, the continued proportion can be written in the form of ca: bc: bd

Ratio and Proportion Formulas

Ratio Formula

Let us consider, we have two quantities and we have to find the ratio of these two, then the formula for ratio is defined as

a: b ⇒ a/b

a, b be two quantities. In this a is called the first term or antecedent and b is called the second term or consequent.

Example: In the Ratio 5:6 5 is called the first term or antecedent and 6 is called the consequent.

If we multiply and divide each term of the ratio by the same number (non-zero), it doesn’t affect the ratio.

Proportion Formula

Consider two ratios are in proportion a:b&c:d the b, c are called means or mean terms and a, d are known as extremes or extreme terms.

a/b = c/d or a : b :: c : d

Example: 3 : 5 :: 4 : 8 in this 3, 8 are extremes and 5, 4 are means

Properties of Proportion

Check out the important list of properties regarding the Proportion Below. They are as follows

• Addendo – If a : b = c : d, then a + c : b + d
• Subtrahendo – If a : b = c : d, then a – c : b – d
• Componendo – If a : b = c : d, then a + b : b = c+d : d
• Dividendo – If a : b = c : d, then a – b : b = c – d : d
• Invertendo – If a : b = c : d, then b : a = d : c
• Alternendo – If a : b = c : d, then a : c = b: d
• Componendo and dividendo – If a : b = c : d, then a + b : a – b = c + d : c – d

Difference Between Ratio and Proportion

Fourth, Third and Mean Proportional

If a : b = c : d, then:

d is called the fourth proportional to a, b, c.
c is called the third proportion to a and b.
Mean proportional between a and b is √(ab).
Comparison of Ratios
If (a:b)>(c:d) = (a/b>c/d)

The compounded ratio of the ratios: (a : b), (c : d), (e : f) is (ace : bdf).

Duplicate Ratios

If a:b is a ratio, then:

• a²:b² is a duplicate ratio
• √a:√b is the sub-duplicate ratio
• a³:b³ is a triplicate ratio

Ratio and Proportion Tricks

Check out the Tricks and Tips to Solve Problems related to Ratio and Proportion. They are as under

• If u/v = x/y, then u/x = v/y
• If u/v = x/y, then uy = vx
• If u/v = x/y, then v/u = y/x
• If u/v = x/y, then (u-v)/v = (x-y)/y
• If u/v = x/y, then (u+v)/v = (x+y)/y
• If u/v = x/y, then (u+v)/ (u-v) = (x+y)/(x-y), it is known as Componendo Dividendo Rule
• If a/(b+c) = b/(c+a) = c/(a+b) and a+b+ c ≠0, then a =b = c

Solved Questions on Ratio and Proportion

1. Are the Ratios 4:5 and 5:10 said to be in Proportion?

Solution:

Expressing the given ratios 4:5 we have 4/5 = 0.8

5:10 = 5/10 = 0.2

Since both the ratios are not equal they are not in proportion.

2. Out of the total students in a class, if the number of boys is 4 and the number of girls being 5, then find the ratio between girls and boys?

Solution:

The ratio between girls and boys is 5:4. The ratio can be written in factor form as 5/4

3. Two numbers are in the ratio 3 : 4. If the sum of numbers is 42, find the numbers?

Solution:

Given 3/4 is the ratio of any two numbers

Let us consider the numbers be 3x and 4x

Given, 3x+4x = 42

7x = 42

x = 42/7

x = 6

finding the numbers we have 3x = 3*6 = 18

4x = 4*6 = 24

Therefore, two numbers are 18, 24

In maths, Numbers are used for common tasks like counting, measurements, and comparisons. A Place Value is a basic mathematical concept, important for every arithmetic math operations. A place value can be represented for both whole numbers and decimals. A place value chart can assist students in identifying and comparing the position of the digits in the given numbers through millions.

The place value of a digit rise by ten times as we move left on the place value chart and drops by ten times as we move right. While representing the number in general form, the place of each digit will be expanded. Let’s understand What is Place Value Chart, what are the systems of place value charts, how to solve the place values explicitly from this article.

Place Value Chart

Place value charts in mathematics support students and even learners to ensure that the digits are in the correct places. To recognize the positional values of numbers correctly, writing the digits in the place value chart is the best way and then address the numbers in the general and the standard form.

Here, we have presented the Indian system place value chart & Internal system place value chart for reference. Go through these two charts and identify the place values of the given number.

Indian Place Value Chart System

It is a chart that represents the value of each digit in a number on the basis of its position. As you noticed in the below Indian place value chart, the nine places are grouped into four periods: Ones, Thousands, Lakhs, and Crores. When reading the number, all digits in the same period are read together as well as with the period name, exclude the one’s period.

Note: If a period contains zero, we do not name that period in the word form.

The Indian System of Place value chart is given below.

Below is an example that shows the relationship between the place or position and the place value of the digits in the given number 13548.

In 13548, 1 is in ten thousand’s place and its place value is 10,000,
3 is in the thousands place and its place value is 3,000,
5 is in the hundreds place and its place value is 500,
4 is in the tens place and its place value is 40,
8 is in one place and its place value is 8.

International Place Value Chart

In the international place value chart, the digits are classified into three periods in a big number. The number is read from left to right as billion, million, thousands, ones.

• 100,000 = 100 thousand
• 1,000,000 = 1 million
• 10,000,000 = 10 millions
• 100,000,000 = 100 millions

The place value chart of the International System is given below:

Comparison Between Indian and International System of Place Value

In this section, you will have a glance at the comparison between both the Indian and International place value system:

Decimals Place Value

In decimals, place value represents the position of each digit after the decimal point and before the decimal point. A place-value chart tells you how many hundreds, tens, and ones to use. The place value of decimals is based on multiplying by 1/10.

Place Value Table

Solved Examples:

Example 1: Find the place value for the number 27349811 in the International place value system & address it with commas and in words.

Solution:

The given number place values representation with commas is 27,349,811 and in words is Twenty-seven million three hundred forty-nine thousand eight hundred eleven.

Example 2: Identify the place value of digits for the given number 13548 using base-ten blocks?

Also, The place value of digits of the number can be positioned using base-ten blocks and aid learners write numbers in their expanded form. The below image has a solution for place value of digits for the given number 13548 using base-ten blocks:

FAQs on Place Value Chart

1. What is Place Value with Example?

The position of each digit in a number is known as a place value. The place value of digits is determined as ones, tens, hundreds, thousands,ten-thousands, and so on, based on their place in the number. For instance, the place value of 7 in 1672 is tens, i.e. 70.

2. What is the place value chart for the number 50?

The place value chart for 50 number is

5 digit – Tens – 50

0 digit – ones – 0

3. Is place value different from face value?

Yes, The place value outlines the position of a digit in the given number but the face value represents the exact value of a digit. As an example here we are taking a number ie., 790, and identify both values of digit 9, the place value of 9 is Tens whereas the face value of 9 is 9.

Trigonometry Ratios Table 0-360: Trigonometry is a branch of mathematics that deals with the study of the length and angles of a triangle. It is usually associated with a right-angle triangle in which one of the angles is 90 degrees. It has a vast number of applications in the field of mathematics. You can figure out many geometrical calculations much simpler if you are aware of the Trigonometric Functions and Table.

Trigonometric Ratios Table help you find the trigonometric standard angles such as 0°, 30°, 45°, 60°, and 90°. You can find Trigonometric Ratios such as sine, cosine, tangent, cosecant, secant, cotangent, etc. In short, you can write the Trigonometric Ratios as sin, cos, tan, cosec, sec, and cot. You can solve Trigonometry Problems easily if you know the standard values of the Trigonometric Ratios. Thus, remember the standard angle values to make your job easier.

Trigonometric Table has a wide range of applications and it was used ever since before the existence of calculators.  Another Important Application of the Trigonometric Table is in the Fast Fourier Transforms.

Trigonometric Ratios Table for Standard Angles

Trig Values Table: 0 to 360 Degrees

Tricks to Remember Trigonometry Table

It is easy to remember the trigonometry table. If you are aware of the trigonometric formulas remembering the table is quite simple. The Trigonometric Ratios Table is dependant on the Trigonometric Formulas. Try to remember the trigonometric table easily by going through the simple formulas.

• sin x = cos (90° – x)
• cos x = sin (90° – x)
• tan x = cot (90° – x)
• cot x = tan (90° – x)
• sec x = cosec (90° – x)
• cosec x = sec (90° – x)
• 1/sin x = cosec x
• 1/cos x = sec x
• 1/tan x = cot x

How to Create a Trigonometric Ratio Table?

Check out the simple guidelines listed below to create a Trigonometric Table having Values of Standard Angles. They are in the following fashion

Step 1:

Create a table having the top row and list out the angles 0°, 30°, 45°, 60°, 90° and also write trigonometric functions such as sin, cos, tan, cosec, sec, cot.

Step 2: Determine the Value of Sin

In the second step determine the value of sin, divide 0, 1, 2, 3, 4 by 4 under the root.

Step 3: Determine the Value of Cos

Cos is opposite to sin and to find the value of cos divide by 4 in the opposite sequence of sin. For instance, divide 4 with 4 under the root to obtain the value of cos 0°

Step 4: Determine the value of tan

Tan is obtained by dividing sin with cos. To find the value of tan 0° divide the Value of Sin 0° by the Value of Cos 0°.

Step 5: Determine the value of the cot

Value of cot is equal to reciprocal of tan. The value of cot at 0° is obtained by dividing 1 with the value of tan at 0°. In the same way, you can find the value of the cot for all the angles.

Step 6: Determine the value of cosec

Cosec value at 0° is the reciprocal of sin at 0°. You can find all the angles of cosec as such

Step 7: Determine the value of sec

sec values can be obtained by the reciprocal values of cos. Sec value at 0° is the opposite of cos on 0°. In the similar way entire table of values is given.

FAQs on Trigonometric Ratios Table

1. How to find the Trigonometric Functions Values?

All the Trigonometric Functions Values can be found easily using the formulas and they are given as such

• Sin = Opposite/Hypotenuse
• Cos = Adjacent/Hypotenuse
• Tan = Opposite/Adjacent
• Cot = 1/Tan = Adjacent/Opposite
• Cosec = 1/Sin = Hypotenuse/Opposite
• Sec = 1/Cos = Hypotenuse/Adjacent

2. What is Trigonometric Values Table?

Trigonometric Values table is made of trigonometric ratios that are interrelated to each other – sine, cosine, tangent, cosecant, secant, cotangent.

3. What are Trigonometric Ratios?

Trigonometric Ratios is a relationship between measurements of length and angles of a right angle triangle.

Whole Numbers is a part of a number system that includes all the positive integers from 0 to infinity. These numbers are present on the number line and are usually called real numbers. Thus, we can say that Whole Numbers are Real Numbers but not all Real Numbers are Whole Numbers. Complete Set of Natural Numbers including “0” are called Whole Numbers.

Whole Numbers – Definition

Whole Numbers are numbers that don’t have fractions and is a collection of positive integers including zero. It is denoted by the symbol “W” and is given as {0, 1, 2, 3, 4, 5, ………}. Zero on a whole denotes null value or nothing.

• Whole Numbers: W = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10……}
• Natural Numbers: N = {1, 2, 3, 4, 5, 6, 7, 8, 9,…}
• Integers: Z = {….-9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,…}
• Counting Numbers: {1, 2, 3, 4, 5, 6, 7,….}

Whole numbers are positive integers along with zero and don’t have fractional or decimal parts. You can perform all the basic operations such as Addition, Subtraction, Multiplication, and Division.

Symbol

The Symbol to denote the Whole Numbers is given by the alphabet W = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,…

• All-natural numbers are whole numbers
• All positive integers including zero are whole numbers
• All whole numbers are real numbers
• All counting numbers are whole numbers

Properties of Whole Numbers

Whole Numbers Properties depend on arithmetic operations such as Addition, Subtraction, Multiplication, Division. When you multiply or add two whole numbers the result will always be a Whole Number. If you Subtract Two Whole Numbers the result may not always be a Whole Number and it can be an Integer too. Division of Whole Numbers can result in a Fraction at times. Let us see few more Properties of Whole Numbers by referring below.

Closure Property: Whole Numbers can be closed under addition or multiplication. If a, b are two whole numbers then a.b and a+b is also a whole number.

Commutative Property of Addition and Multiplication: Sum and Product of Two Whole Numbers will be the same no matter the order in which they are added or multiplied. If a, b are two whole numbers then a+b = b+a, a.b = b.a

Additive Identity: If a Whole Number is added to 0 the result remains unchanged. If a is a whole number then a+0 = 0+a = a

Multiplicative Identity: Whenever you multiply a whole number with 1 the result remains unchanged. Let us consider a whole number “a” then a.1 = 1. = a

Associative Property: If you are grouping the whole numbers and adding or multiplying a set the result remains the same irrespective of the order. If a, b, c are whole numbers then a + (b + c) = (a + b) + c and a. (b.c)=(a.b).c

Distributive Property: If a, b, c are three whole numbers then the distributive property of multiplication over addition is given by a.(b+c) =(a.b)+(a.c), Similarly Distributive Propoerty of Multiplication over Subtraction is given by a.(b-c) = (a.b)-(a.c)

Multiplication by Zero: If you multiply a Whole Number with Zero the result is always zero. i.e. a.0=0.a=0

Division by Zero: If you divide a Whole Number with Zero the result is undefined, i.e. a divided by 0 is not defined.

Difference between Natural Numbers and Whole Numbers

By referring to the below sections you will better understand the difference between Whole Numbers and Natural Numbers.

Solved Examples on Whole Numbers

1. Are 101, 147, 193, 4028 whole numbers?

Yes, 101, 147, 193, 4028 are all whole numbers.

2. Solve 8 × (3 + 12) using the Distributive Property?

We know as per the Distributive Property a.(b+c) =(a.b)+(a.c)

Applying the Input Numbers in the formula we have the equation as such

8 × (3 + 12) = 8*3 +8*12

= 24+108

= 132

FAQs on Whole Numbers

1. Is 0 a Whole Number?

Yes, 0 is a Whole Number.

2. What is the Symbol of Whole Numbers?

The Letter W represents the Whole Numbers.

3. Are all Natural Numbers Whole Numbers?

Yes, all Natural Numbers are Whole Numbers but not all Whole Numbers are Natural Numbers. Natural Numbers begin from 0 and counts till infinity. Whole Numbers begin from 0 and end at infinity.

4. What is the set of whole numbers?

The whole numbers are the natural numbers together with 0. The set of whole numbers is a subset of the integers but does not include the negative integers.

Basically, Standard Form in Maths can be represented for numbers like decimal numbers, rational numbers, fractions, polynomials, equations, linear equations, etc. As we all know that the simplified form of the fractions called decimal numbers. Eventually, we can say that standard form is the representation of large numbers in small numbers irrespective of any form of numbers. In this article, we have explained what is the standard form of numbers, decimals, equations, etc. How to do it, Rules, and solved Standard form examples.

So, Let’s dive into it!

What is Standard Form?

A Standard Form is a process of formulating a given mathematical concept such as number, equation, polynomial, etc. in the standard form by following certain basic rules.

Standard Form of a Number

The definition of the standard form of a number is representing the very large expanded number in a small number. Here, we will see how to write a numerical in standard form with an example.

Now, we are taking a large number in the expanded form and convert the number into standard form.

Example: 

Write the given expanded form into standard form.

10,00,00,000 + 5,00,00,000 + 4,00,000 + 80,000 + 2,000 + 60 + 9.

Solution:

With the help of this below table, we will write the given expanded form of number into the standard form of a number.

Expanded Form                                                                                                   Standard Form

10,00,00,000 + 5,00,00,000 + 4,00,000 + 80,000 + 2,000 + 60 + 9       =             150482069

Standard Form of a Decimal Number

In Britain, the Scientific Notation’s other name is the Standard Form. And in other countries, it means not in the form of the large expanded number. We all know that it’s tough to read numbers such as 0.000000002345678 or 12345678900000. In order to help you all while reading these large numbers, we convert them into standard form.

Any number which we will address as a decimal number, among 1.0 and 10.0, multiplied by a power of 10, is stated to be in standard form. For example, 0.67X10¹³ is in the standard form.

Example:

Write down the standard form of the given decimal number 5326.6?

Solution:

The given decimal number 5326.6 can be written in this way in a scientific notation:

Because 5326.6 = 53266 X 1000 =  5.3266 × 10^3.

Standard Form of a Linear Equation

The “Standard Form” for writing down a Linear Equation is Ax + By = C

A shouldn’t be negative, A and B shouldn’t both be zero, and A, B, and C should be integers.

Example:

Put this y = 7x + 4 in linear equation standard form?

Solution:

Given equation is Y= 7x + 4

Now, you have to change 7x from right to left like this, −7x + y = 4

Multiply all by −1:

7x − y = −4

Note: A = 7, B = −1, C = −4.

Standard Form of a Quadratic Equation

The Standard Form for writing down a Quadratic Equation is ax^2 + bx + c = 0, a is not equal to 0.

Example: 

Put this equation x(x−1) = 4 in the standard form?

Solution:

Given equation is x(x−1) = 4

In the first step, you have to expand x(x−1):

x(x−1) = x² − x

x² − x = 4

Next step is to move the 4 numerical to left side,

x² − x − 4 = 0.

Where A=1, B= -1, C= -4

The standard form of a quadratic equation x(x−1) = 4 is x² − x − 4 = 0. 

FAQs on Standard Form Rules in Maths

1. What is the standard form of an Equation?

An Equation in Standard Form looks like (some expression) = 0 ie., x + y = 0, where the left side of an equation are x and y terms and the Zero is on the right side.

2. What is meant by the standard form of a circle?

The graph of a circle is fully defined by its center and radius. The standard form for the equation of a circle is (x−h)²+(y−k)²=r². The center is (h,k) and the radius measures r units.

3. How to write 81 900 000 000 000 in standard form?

Steps on how to find or write the standard form of a given number ie., 81 900 000 000 000:

• In step-1, write the first digit 8
• Now, add a point then it becomes 8.
• Count the remaining digits after the digit 8 and write the count in the power of 10.
• For this example, there are 13 digits. So, the standard form of 81 900 000 000 000 is 8.19 × 10¹³.

According to Demorgan’s Law Complement of Union of Two Sets is the Intersection of their Complements and the Complement of Intersection of Two Sets is the Union of Complements. The Law can be expressed as such ( A ∪ B) ‘ = A ‘ ∩ B ‘. By referring to the further modules you can find Demorgan’s Law Statement, Proof along with examples.

For any two finite sets A and B, we have

(i) (A U B)’ = A’ ∩ B’ (which is a De Morgan’s law of union).

(ii) (A ∩ B)’ = A’ U B’ (which is a De Morgan’s law of intersection).

De Morgan’s Laws Statement and Proof

A Set is a well-defined collection of objects or elements. You can perform various operations on sets such as Complement, Union, and Intersection. These Operations and usage can be further simplified by a set of simple laws called Demorgan’s Laws.

Any Set that includes all the elements related to a particular context is called a universal set. Let us assume a Universal Set U such that A and B are Subsets of it.

De Morgan’s Law Proof: (A∪B)’= A’∩ B’   

As per Demorgan’s First Law, the Complement of Union of Two Sets A and B is equal to the Intersection of Complements of Sets A and B.

(A∪B)’= A’∩ B’

Let P = (A U B)’ and Q = A’ ∩ B’

Consider x to be an arbitrary element of P then x ∈ P ⇒ x ∈ (A U B)’

⇒ x ∉ (A U B)

⇒ x ∉ A and x ∉ B

⇒ x ∈ A’ and x ∈ B’

⇒ x ∈ A’ ∩ B’

⇒ x ∈ Q

Therefore, P ⊂ Q …………….. (i)

Let us consider y to be an arbitrary element of Q then y ∈ Q ⇒ y ∈ A’ ∩ B’

⇒ y ∈ A’ and y ∈ B’

⇒ y ∉ A and y ∉ B

⇒ y ∉ (A U B)

⇒ y ∈ (A U B)’

⇒ y ∈ P

Therefore, Q ⊂ P …………….. (ii)

Combining (i) and (ii) we get; P = Q i.e. (A U B)’ = A’ ∩ B’

De Morgan’s Law Proof: (A ∩ B)’ = A’ U B’

Let us consider Sets M = (A ∩ B)’ and N = A’ U B’

Let x be an arbitrary element of M then x ∈ M ⇒ x ∈ (A ∩ B)’

⇒ x ∉ (A ∩ B)

⇒ x ∉ A or x ∉ B

⇒ x ∈ A’ or x ∈ B’

⇒ x ∈ A’ U B’

⇒ x ∈ N

Thus, M ⊂ N …………….. (i)

Again, let y be an arbitrary element of N then y ∈ N ⇒ y ∈ A’ U B’

⇒ y ∈ A’ or y ∈ B’

⇒ y ∉ A or y ∉ B

⇒ y ∉ (A ∩ B)

⇒ y ∈ (A ∩ B)’

⇒ y ∈ M

Thus, N ⊂ M …………….. (ii)

Combining (i) and (ii) we get; M = N i.e. (A ∩ B)’ = A’ U B’

Examples of De Morgan’s Law

1. If U = {a,b,c, d, e}, X = {b, c, d} and Y = {b, d, e}. Prove that De Morgan’s law: (X ∩ Y)’ = X’ U Y’?

Solution:

Given Sets are U = {a,b,c, d, e}, X = {b, c, d} and Y = {b, d, e}

Firstly find the (X ∩ Y) = {b, c, d} ∩ {b, d, e}

= { b,d}

(X ∩ Y)’ = U – (X ∩ Y)

= {a,b,c, d, e} – { b,d}

= {a,c,e}

X’ =  U – X

= {a,b,c, d, e} – {b, c, d}

= {a,e}

Y’ = U – Y

= {a,b,c, d, e} – {b, d, e}

= {a,c}

X’ U Y’ = {a,e} U {a,c}

= {a,c,e}

Hence Prooved (X ∩ Y)’ = X’ U Y’

2. Let U = {1, 2, 3, 4, 5, 6, 7, 8}, A = {2, 3, 4} and B = {5, 6, 8}. Show that (A ∪ B)’ = A’ ∩ B’?

Solution:

Given Sets are U = {1, 2, 3, 4, 5, 6, 7, 8}, A = {4, 5, 6} and B = {5, 6, 8}
(A ∪ B) = {4, 5, 6} ∪ {5, 6, 8}

= {4, ,5, 6, 8}

(A ∪ B)’ = U – (A ∪ B)

= {1, 2, 3, 4, 5, 6, 7, 8} – {4, ,5, 6, 8}

= {1, 2, 3,7}

A’ = U – A

= {1, 2, 3, 4, 5, 6, 7, 8} – {4, 5, 6}

= {1, 2, 3, 7, 8}

B’ = U – B

= {1, 2, 3, 4, 5, 6, 7, 8} – {5, 6, 8}

= {1, 2, 3, 4, 7}

A’ ∩ B’ = {1, 2, 3, 7, 8} ∩ {1, 2, 3, 4, 7}

= {1, 2, 3, 7}

Hence Prooved (A ∪ B)’ = A’ ∩ B’

Binary Subtraction is one among the four binary operations in which we perform subtraction of binary numbers i.e. 0 or 1. It is similar to the Basic Arithmetic Operation of Decimals. When we subtract 1 from 0 we need to borrow 1 from the next digit to reduce the digit by 1 and the remainder left here is 1. Go through the entire article to know about Binary Subtraction Rules, Subtraction Table, Tricks and Procedure on How to Subtract Binary Numbers, etc.

What is meant by Binary Subtraction?

Binary Numbers Subtraction is similar to Subtraction of Decimals or Base 10 Numbers. For instance, 1+1+1 is 3 in base 10 whereas in a binary number system 1+1+1 is 11. While Performing Addition and Subtraction in Binary Numbers be careful with borrowing as you might need to do them quite often.

While performing subtraction of several columns of binary digits you need to consider the borrowing. If you subtract 1 from 0 the result will be 1 where 1 is borrowed from the next highest order digit.

Binary Subtraction Table

On Adding Two Binary Numbers 1 and 1 we get the result 10 in which we consider 0 and carry forward 1 to the next higher-order bit. On Subtracting 1 from 1, the result is 0 and nothing will be carry forwarded.

While subtracting 1 from 0 in the case of decimal numbers we borrow 1 from the preceding higher-order number and make it 10 and after subtracting result becomes 9. However, in the case of Binary Subtraction, the result is 0.

Rules for Binary Subtraction

Binary Subtraction is quite simple compared to Decimal Subtraction if you remember the following tips and tricks.

0 – 0 = 0
0 – 1 = 1 ( with a borrow of 1)
1 – 0 = 1
1 – 1 = 0

You can look at the binary subtraction examples provided below for better understanding.

How to Subtract Binary Numbers?

Follow the below-listed steps to perform Binary Subtraction. You will find the Subtraction of Binary Numbers much easier after going through the below steps. They are as follows

• Align the numbers similar to an ordinary subtraction problem. Write the larger number up and the smaller number below it. If the Smaller Digit has few digits align them towards the right same as in decimal subtraction.
• Begin from the right column and perform the subtraction operation of binary numbers. While doing so keep the binary subtraction rules in mind and do accordingly.
• Solve column by column moving from right to left.

Binary Subtraction Examples

1. Find the Value of 1010011 – 001110?

Solution:

Write the given numbers as if you subtracting decimal numbers. Align them to the right and fill them with leading zeros so that both the numbers have the same digits.

1011011

(-)0001010

——————

1010001

Binary Notation

Decimal Notation

The decimal Equivalent of given numbers is

1011011 = 91

001010 = 10

91-10 = 81

2. Find the value of 1100010 – 001000?

Solution:

Write the given numbers as if you subtracting decimal numbers. Align them to the right and fill them with leading zeros so that both the numbers have the same digits.

1100010

(-)0001000

——————

1,011,010

Decimal Notation

The decimal Equivalent of given numbers is

1100010 = 98

1000 = 8

98-8 = 90

Binary Subtraction using 1’s Complement

Go through the below procedure and perform the Binary Subtraction easily. They are as follows

• Firstly, write the 1’s complement of the subtrahend.
• And then add the 1’s complement subtrahend with the minuend.
• If the result has a carryover add the carryover in the least significant bit.
• If it has no carryover take the 1’s complement of resultant and it is negative.

Questions on Binary Subtraction using 1’s Complement

1. (11001)₂  – (1010)₂

Solution:

(11001)₂  = 25

(1010)₂  = 10 – subtrahend

Fill with leading zeros till you have the same number of digits in both the numbers. Firstly, take the 1’s complement of subtrahend i.e. (01010)₂.

1’s complement of the subtrahend is 10101. Add 1 to the 1’s complement of the second number

10101
+   1
↓
10110

Now instead of subtracting add the 1’s complement of the second number to the first one

11001
+ 10110

——————
101111

Remove the leading 1 to obtain the result.

Then, remove the leading zeros as it will not alter the result and you can write the final result of subtraction as such

11001
– 1010

——————

1111

FAQs on Binary Subtraction

1. What are the Rules of Binary Subtraction?

Rules of Binary Subtraction are as follows

0 – 0 = 0
0 – 1 = 1 ( with a borrow of 1)
1 – 0 = 1
1 – 1 = 0

2. How many basic binary subtraction combinations are possible?

There are four possible binary subtraction combinations when subtracting binary digits.

3. What signs does the binary digit 0 and 1 represent?

0 represents the positive sign and 1 represents the negative sign.

Mathematics is the study of numbers, shapes, and patterns. It includes various complex and simple arithmetic topics that help people in their daily life routine. In Maths, Numbers play a major role and they can be of different types like Real Numbers, Whole Numbers, Natural Numbers, Decimal Numbers, Rational Numbers, etc. Today, we are going to discuss one of the main topics of Decimal Numbers. In Decimals, identifying the Decimal Place Values is a fundamental topic and everyone should know the techniques clearly. So, here we will be discussing elaborately the topic of Decimal Place Values Chart.

Let’s get into it.

What is the Place Value of Decimals?

Place value is a positional notation system where the position of a digit in a number, determines its value. The place value for decimal numbers is arranged exactly the identical form of treating whole numbers, but in this case, it is reverse. On the basis of the preceding exponential of 10, the place value in decimals can be decided.

Decimal Place Value Chart

On the place value chart, the numbers on the left of the decimal point are multiplied with increasing positive powers of 10, whereas the digits on the right of the decimal point are multiplied with increasing negative powers of 10 from left to right.

• The first digit after the decimal represents the tenths place.
• The second digit after the decimal represents the hundredths place.
• The third digit after the decimal represents the thousands place.
• The rest of the digits proceed to fill in the place values until there are no digits left.

How to write the place value of decimals for the number 132.76?

• The place of 6 in the decimal 132.76 is 6/100
• The place of 7 in the decimal 132.76 is 7/10
• The place of 2 in the decimal 132.76 is 2
• The place of 3 in the decimal 132.76 is 30
• The place of 1 in the decimal 132.76 is 100.

Examples:

1.  Write the place value of digit 7 in the following decimal number: 5.47?

The number 7 is in the place of hundredths, and its place value is 7 x 10 ^-2 = 7/100 = 0.07.

2. Identify the place value of the 6 in the given number: 689.87?

Given number is 689.87

The place of 6 in the decimal 689.87 is 600 or 6 hundreds. 

3. Write the following numbers in the decimal place value chart.

(i) 4532.079

(ii) 490.7042

Solutions: 

(i) 4532.079

4532.079 in the decimal place value chart.

(ii) 490.7042

490.7042 in the decimal place value chart.

In your day-to-day life, you might need to convert from one unit to another. To Perform the Required Calculations you might need to learn about Mathematical Conversions. Thus, it is necessary to learn about Unit Conversions to change from one unit to another unit.  Before understanding the Units of Measurement you need to be aware of the relationship between them.

Go through the entire article to learn about units of length conversion chart, unit of mass and weight conversion chart, unit of time conversion chart, units of capacity and volume conversion chart, unit of a temperature conversion chart, etc. Math Conversion Charts are quite important and interesting to learn.

What is Conversion of Units?

Depending on the Situation each unit differs. For instance, the area of the room is expressed in Meters whereas the thickness of the pencil is expressed in mm. Thus, it is necessary to convert from one unit to another.

Importance of Mathematical Conversions

In Order to have accuracy and avoid confusion in measurement, we need to change from one unit to another. For example, we will measure the length of the pencil in cm but no in km. Likewise, we need to convert from one unit to another. While converting from one unit to another of the same quantity we use multiplicative conversion factors. Let’s see how to convert different units of length and mass in the later modules.

Length Conversion Chart

Mass Conversion Chart

Unit Conversion Table

Length Conversion Table

Mass Conversion Table

Capacity Conversion Table

Points to remember:

• To convert bigger units to smaller units multiply
• To convert smaller units to bigger units divide

Solved Examples on Conversion of Units

1. Convert 4 cm to km?

Solution:

Step 1:

Draw a line or box as below

Step 2:

Put 1 at the larger unit to be converted.

Here we want to convert cm to km,

Since km is the larger unit, thus put 1 under the corresponding column (km).

Step 3:

Now place 0 till the smaller unit

Since the conversion is from a smaller unit to larger we need to divide the given length by 100000 i.e. 10⁵

4 cm = 4/10⁵

= 0.00004 km

2. Convert 7 gms to milligrams?

Solution:

We need to convert grams to milligrams

We know 1 gram = 1000 mg

Thus 7 g = 7*1000

= 7000 mg