Eureka Math

Engage NY Eureka Math 7th Grade Module 5 Lesson 10 Answer Key

Eureka Math Grade 7 Module 5 Lesson 10 Example Answer Key

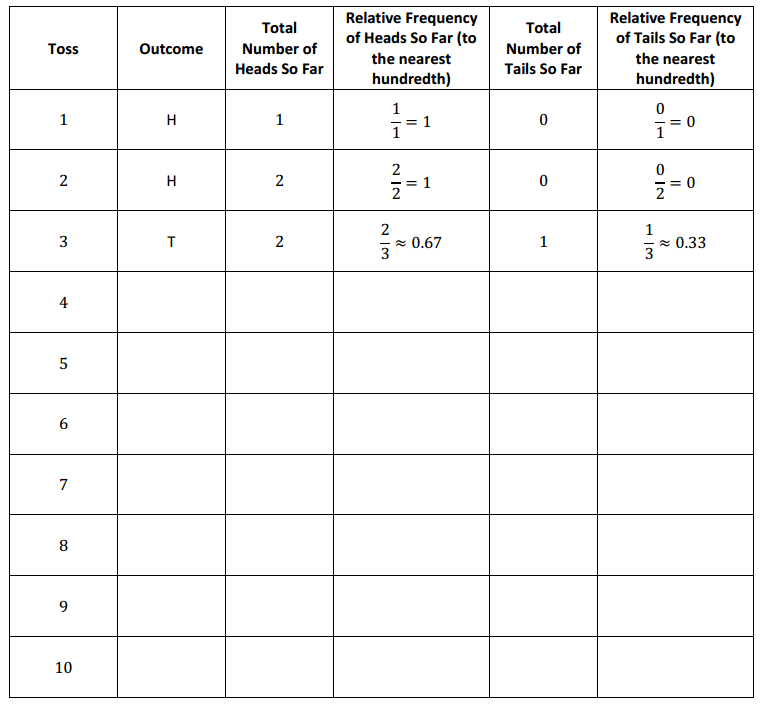
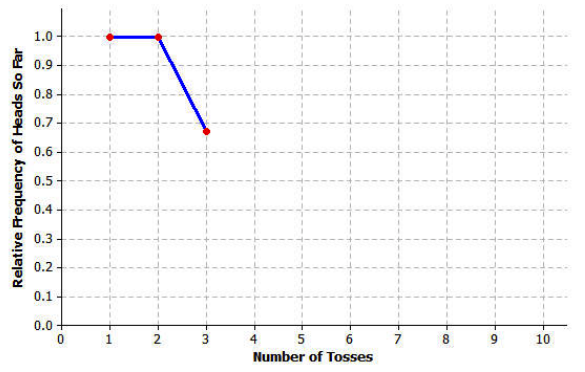
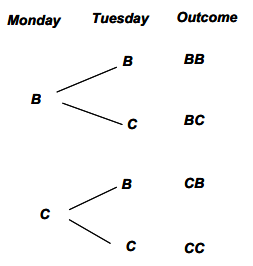
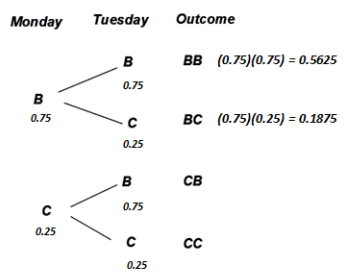
Example 1: Families
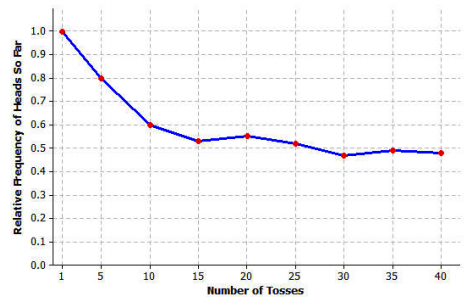
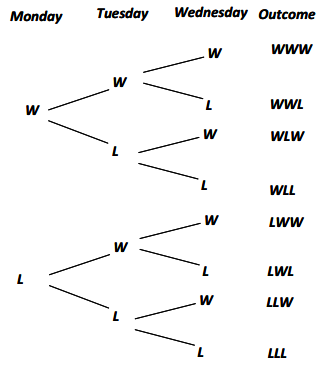
How likely is it that a family with three children has all boys or all girls?
Let’s assume that a child is equally likely to be a boy or a girl. Instead of observing the result of actual births, a toss of a fair coin could be used to simulate a birth. If the toss results in heads (H), then we could say a boy was born; if the toss results in tails (T), then we could say a girl was born. If the coin is fair (i.e., heads and tails are equally likely), then getting a boy or a girl is equally likely.
Answer:
Pose the following questions to the class one at a time, and allow for multiple responses:
→ How could a number cube be used to simulate getting a boy or a girl birth?
An even-number outcome represents boy, and an odd-number outcome represents girl; a prime-number outcome represents boy, and a non-prime outcome represents girl; or any three-number cube digits represents boy, while the rest represents girl.

→ How could a deck of cards be used to simulate getting a boy or a girl birth?
The most natural option is to allow black cards to represent one gender and red cards to represent the other.

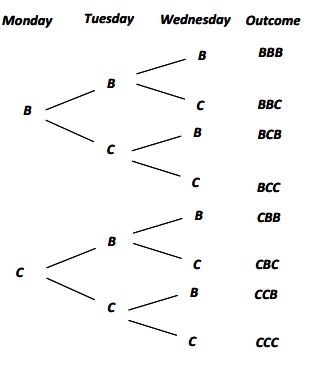
Example 2.
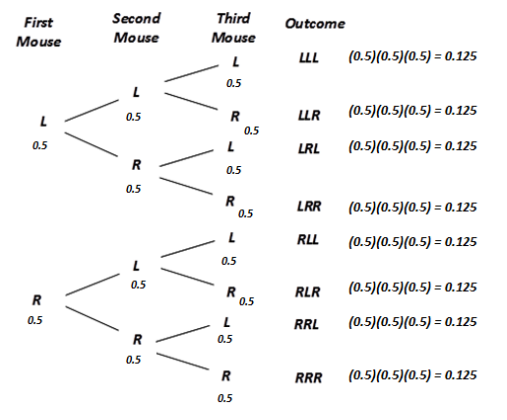
Simulation provides an estimate for the probability that a family of three children would have three boys or three girls by performing three tosses of a fair coin many times. Each sequence of three tosses is called a trial. If a trial results in either HHH or TTT, then the trial represents all boys or all girls, which is the event that we are interested in. These trials would be called a success. If a trial results in any other order of H’s and T’s, then it is called a failure.

The estimate for the probability that a family has either three boys or three girls based on the simulation is the number of successes divided by the number of trials. Suppose 100 trials are performed, and that in those 100 trials, 28 resulted in either HHH or TTT. Then, the estimated probability that a family of three children has either three boys or three girls would be \(\frac{28}{100}\), or 0.28.
Answer:
→ What is the estimated probability that the three children are not all the same gender?
1 – 0.28 = 0.72

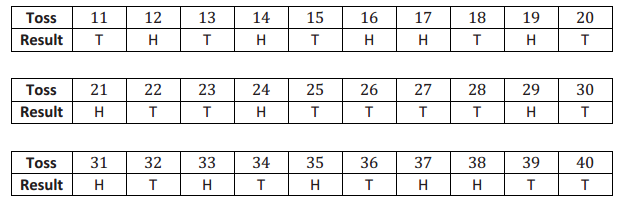
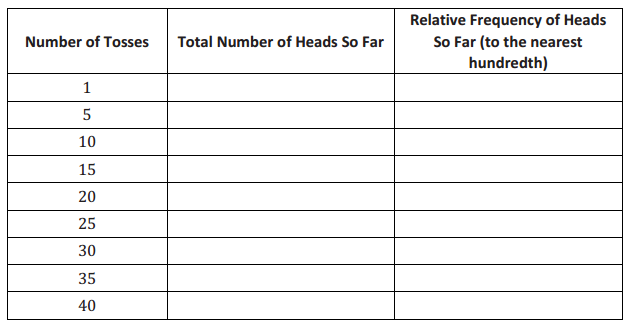
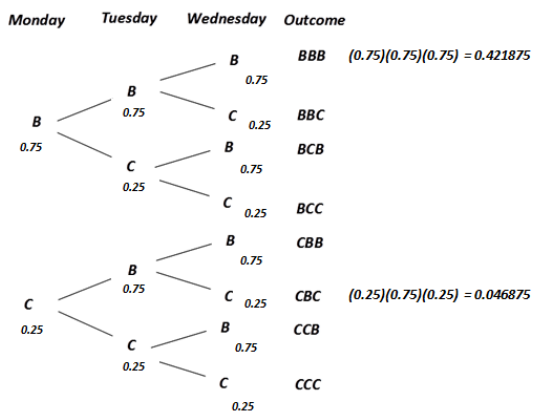
Example 3: Basketball Player
Suppose that, on average, a basketball player makes about three out of every four foul shots. In other words, she has a 75% chance of making each foul shot she takes. Since a coin toss produces equally likely outcomes, it could not be used in a simulation for this problem.

Instead, a number cube could be used by specifying that the numbers 1, 2, or 3 represent a hit, the number 4 represents a miss, and the numbers 5 and 6 would be ignored. Based on the following 50 trials of rolling a fair number cube, find an estimate of the probability that she makes five or six of the six foul shots she takes.

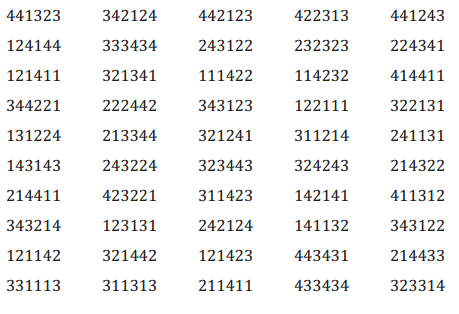
Answer:
50 trials of six numbers each are shown. Students are to estimate the probability that the player makes five or six of the six shots she takes. So, they should count how many of the trials have five or six of the numbers 1, 2, 3 in them as successes. They should find the estimated probability to be \(\frac{27}{50}\), or 0.54.

The estimate of the probability that she will make five or six foul shots is \(\frac{27}{50}\).

Eureka Math Grade 7 Module 5 Lesson 10 Exercise Answer Key

Exercises 1–2
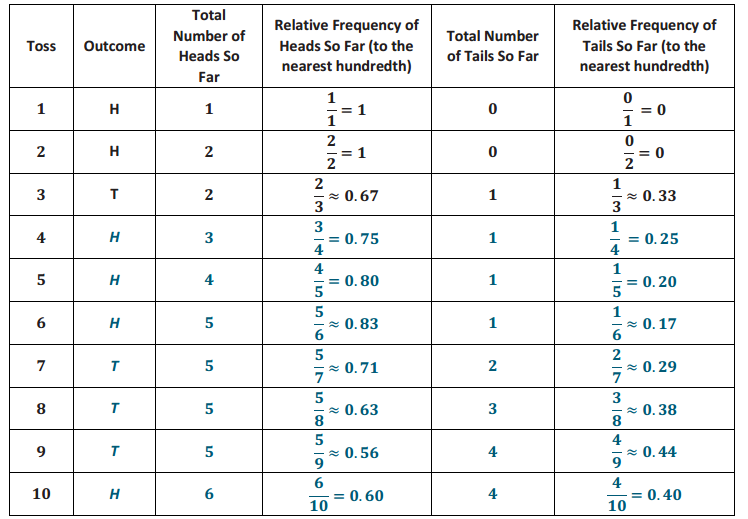
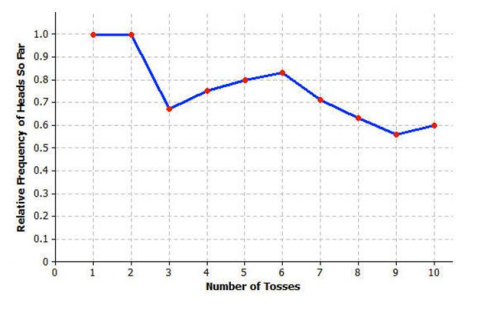
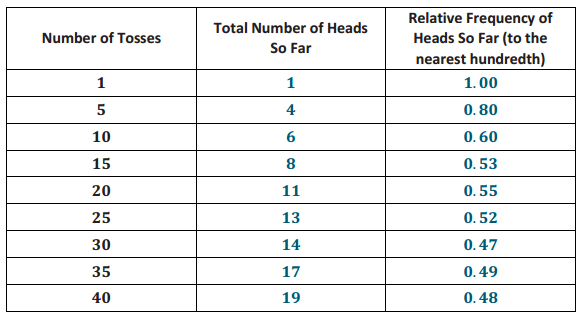
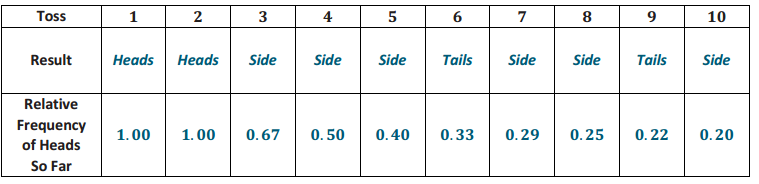
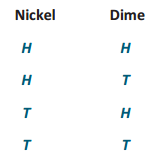
Suppose that a family has three children. To simulate the genders of the three children, the coin or number cube or a card would need to be used three times, once for each child. For example, three tosses of the coin resulted in HHT, representing a family with two boys and one girl. Note that HTH and THH also represent two boys and one girl.

Exercise 1.
Suppose that when a prime number (P) is rolled on the number cube, it simulates a boy birth, and a non-prime (N) simulates a girl birth. Using such a number cube, list the outcomes that would simulate a boy birth and those that simulate a girl birth. Are the boy and girl birth outcomes equally likely?
Answer:
The outcomes are 2, 3, 5 for a boy birth and 1, 4, 6 for a girl birth. The boy and girl births are thereby equally likely.

Exercise 2.
Suppose that one card is drawn from a regular deck of cards. A red card (R) simulates a boy birth, and a black card (B) simulates a girl birth. Describe how a family of three children could be simulated.
Answer:
The key response has to include the drawing of three cards with replacement. If a card is not replaced and the deck shuffled before the next card is drawn, then the probabilities of the genders have changed (ever so slightly, but they are not 50/50 from draw to draw). Simulating the genders of three children requires three cards to be drawn
with replacement.

Exercises 3–5
Exercise 3.
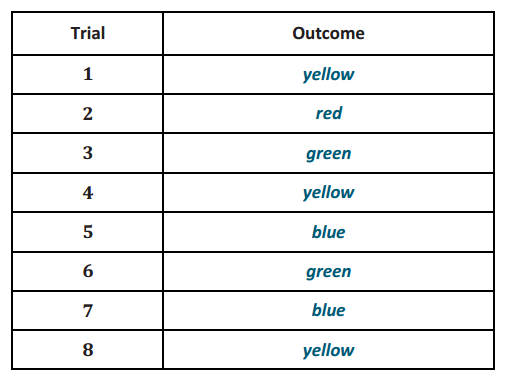
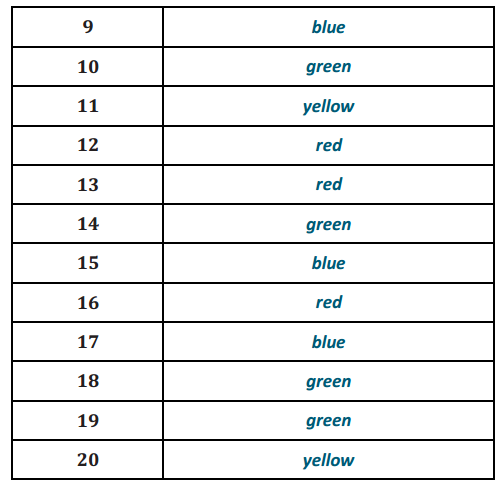
Find an estimate of the probability that a family with three children will have exactly one girl using the following outcomes of 50 trials of tossing a fair coin three times per trial. Use H to represent a boy birth and T to represent a girl birth.

Answer:
T represents a girl. I went through the list, counted the number of times that HHT, HTH, or THH appeared and divided that number of successes by 50. The simulated probability is \(\frac{16}{50}\), or 0.32

Exercise 4.
Perform a simulation of 50 trials by rolling a fair number cube in order to find an estimate of the probability that a family with three children will have exactly one girl.
a. Specify what outcomes of one roll of a fair number cube will represent a boy and what outcomes will represent a girl.
b. Simulate 50 trials, keeping in mind that one trial requires three rolls of the number cube. List the results of your 50 trials.
c. Calculate the estimated probability.
Answer:
Answers will vary. For example, students could identify a girl birth as 1, 2, 3 outcome on one roll of the number cube and roll the number cube three times to simulate three children (one trial). They need to list their 50 trials. Note that an outcome of 412 would represent two girls, 123 would represent three girls, and 366 would represent one girl, as would 636 and 663. Be sure that they are clear about how to do all five steps of the simulation process.

Exercise 5.
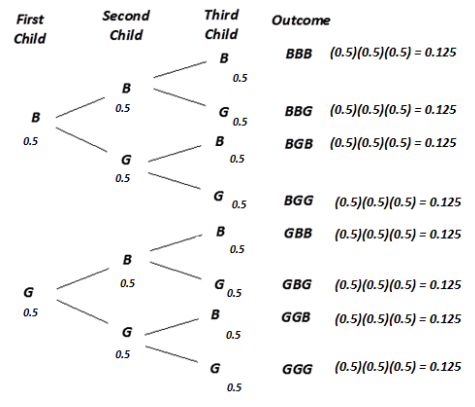
Calculate the theoretical probability that a family with three children will have exactly one girl.
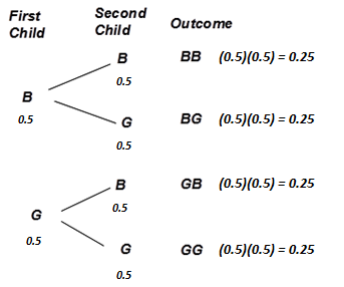
a. List the possible outcomes for a family with three children. For example, one possible outcome is BBB (all three children are boys).
b. Assume that having a boy and having a girl are equally likely. Calculate the theoretical probability that a family with three children will have exactly one girl.
c. Compare it to the estimated probabilities found in parts (a) and (b).
Answer:
a. The sample space is BBB, BBG, BGB, GBB, BGG, GBG, GGB, GGG.
b. Each is equally likely, so the theoretical probability of getting exactly one girl is \(\frac{3}{8}\), or 0.375 (BBG, BGB, GBB).
c. Answers will vary. The estimated probabilities from the first two parts of this exercise should be around 0.375. If not, suggest that students conduct more trials.

Eureka Math Grade 7 Module 5 Lesson 10 Problem Set Answer Key

Question 1.
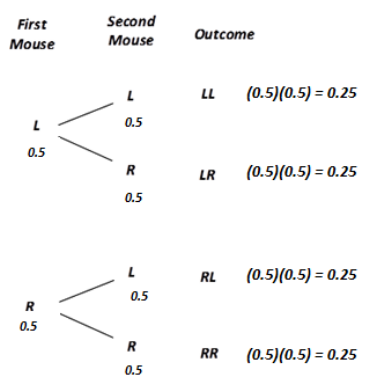
A mouse is placed at the start of the maze shown below. If it reaches station B, it is given a reward. At each point where the mouse has to decide which direction to go, assume that it is equally likely to go in either direction. At each decision point 1, 2, 3, it must decide whether to go left (L) or right (R). It cannot go backward.

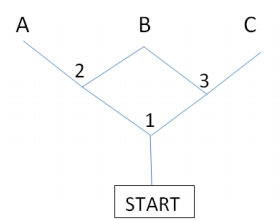
a. Create a theoretical model of probabilities for the mouse to arrive at terminal points A, B, and C.
i) List the possible paths of a sample space for the paths the mouse can take. For example, if the mouse goes left at decision point 1 and then right at decision point 2, then the path would be denoted LR.
ii) Are the paths in your sample space equally likely? Explain.
iiii) What are the theoretical probabilities that a mouse reaches terminal points A, B, and C? Explain.

b. Based on the following set of simulated paths, estimate the probabilities that the mouse arrives at points A, B, and C.

c. How do the simulated probabilities in part (b) compare to the theoretical probabilities of part (a)?
Answer:
a. i) The possible paths in the sample space are {LL, LR, RL, RR}.
ii) Each of these outcomes has an equal probability of 1/4 since at each decision point there are only two possible choices, which are equally likely.
iii) The probability of reaching terminal point A is \(\frac{1}{4}\) since it is accomplished by path LL. Similarly, reaching terminal point C is \(\frac{1}{4}\) since it is found by path RR. However, reaching terminal point B is \(\frac{1}{2}\) since it is reached via LR or RL.

b. Students need to go through the list and count the number of paths that go to A, B, and C. They should find the estimated probabilities to be \(\frac{8}{40}\), or 0.2, for A, \(\frac{22}{40}\), or 0.55, for B, and \(\frac{10}{40}\), or 0.25, for C.

c. The probabilities are reasonably close for parts (a) and (b). Probabilities based on taking 400 trials should be closer than those based on 40, but the probabilities based on 40 are in the ballpark.

Question 2.
Suppose that a dartboard is made up of the 8 × 8 grid of squares shown below. Also, suppose that when a dart is thrown, it is equally likely to land on any one of the 64 squares. A point is won if the dart lands on one of the 16 black squares. Zero points are earned if the dart lands in a white square.

a. For one throw of a dart, what is the probability of winning a point? Note that a point is won if the dart lands on a black square.
b. Lin wants to use a number cube to simulate the result of one dart. She suggests that 1 on the number cube could represent a win. Getting 2, 3, or 4 could represent no point scored. She says that she would ignore getting a 5 or 6. Is Lin’s suggestion for a simulation appropriate? Explain why you would use it, or if not, how you would change it.
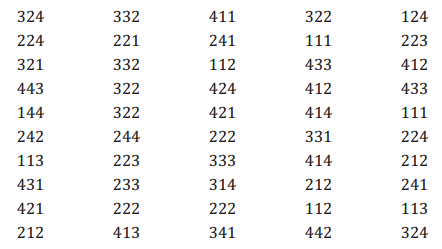
c. Suppose a game consists of throwing a dart three times. A trial consists of three rolls of the number cube. Based on Lin’s suggestion in part (b) and the following simulated rolls, estimate the probability of scoring two points in three darts.

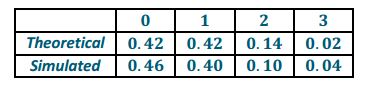
d. The theoretical probability model for winning 0, 1, 2, and 3 points in three throws of the dart as described in this problem is:
i) Winning 0 points has a probability of 0.42.
ii) Winning 1 point has a probability of 0.42.
iii) Winning 2 points has a probability of 0.14.
iv) Winning 3 points has a probability of 0.02.
Use the simulated rolls in part (c) to build a model of winning 0, 1, 2, and 3 points, and compare it to the theoretical model.
Answer:
a. The probability of winning a point is \(\frac{16}{64}\), or 0.25.

b. Lin correctly suggests that to simulate the result of one throw, a number cube could be used with the 1 representing a hit; 2, 3, 4 representing a missed throw; and 5 and 6 being ignored. (As an aside, a tetrahedron could be used by using the side facing down as the result.)

c. The probability of scoring two points in three darts is \(\frac{5}{50}\), or 0.1. (Students need to count the number of trials that contain exactly two 1’s.)

d. To find the estimated probability of 0 points, count the number of trials that have no 1’s in them
(\(\frac{23}{50}\) = 0.46).
To find the estimated probability of 1 point, count the number of trials that have one 1 in them (\(\frac{20}{50}\) = 0.4).
From part (c), the estimated probability of 2 points is 0.1.
To find the estimated probability of 3 points, count the number of trials that have three 1’s in them
(\(\frac{2}{50}\) = 0.04).
The theoretical and simulated probabilities are reasonably close.

Eureka Math Grade 7 Module 5 Lesson 10 Exit Ticket Answer Key

Question 1.
Nathan is your school’s star soccer player. When he takes a shot on goal, he typically scores half of the time. Suppose that he takes six shots in a game. To estimate the probability of the number of goals Nathan makes, use simulation with a number cube. One roll of a number cube represents one shot.
a. Specify what outcome of a number cube you want to represent a goal scored by Nathan in one shot.
b. For this problem, what represents a trial of taking six shots?
c. Perform and list the results of ten trials of this simulation.
d. Identify the number of goals Nathan made in each of the ten trials you did in part (c).
e. Based on your ten trials, what is your estimate of the probability that Nathan scores three goals if he takes six shots in a game?
Answer:
a. Answers will vary; students need to determine which three numbers on the number cube represent scoring a goal.
b. Rolling the cube six times represents taking six shots on goal or 1 simulated trial.
c. Answers will vary; students working in pairs works well for these problems. Performing only ten trials is a function of time. Ideally, many more trials should be done. If there is time, have the class pool their results.
d. Answers will vary.
e. Answers will vary; the probability of scoring per shot is \(\frac{1}{2}\).

Question 2.
Suppose that Pat scores 40% of the shots he takes in a soccer game. If he takes six shots in a game, what would one simulated trial look like using a number cube in your simulation?
Answer:
Students need to realize that 40% is 2 out of 5. In order to use the number cube as the device, 1 and 2 could represent goals, while 3, 4, and 5 could represent missed shots, and 6 is ignored. Rolling the number cube six times creates 1 simulated trial.

Engage NY Eureka Math 7th Grade Module 5 Lesson 8 Answer Key

Eureka Math Grade 7 Module 5 Lesson 8 Example Answer Key

Coins were discussed in previous lessons of this module. What is special about a coin? In most cases, a coin has two different sides: a head side (heads) and a tail side (tails). The sample space for tossing a coin is {heads, tails}. If each outcome has an equal chance of occurring when the coin is tossed, then the probability of getting heads is \(\frac{1}{2}\), or 0.5. The probability of getting tails is also 0.5. Note that the sum of these probabilities is 1.

The probabilities formed using the sample space and what we know about coins are called the theoretical probabilities. Using observed relative frequencies is another method to estimate the probabilities of heads or tails. A relative frequency is the proportion derived from the number of the observed outcomes of an event divided by the total number of outcomes. Recall from earlier lessons that a relative frequency can be expressed as a fraction, a decimal, or a percent. Is the estimate of a probability from this method close to the theoretical probability? The following example investigates how relative frequencies can be used to estimate probabilities.

Beth tosses a coin 10 times and records her results. Here are the results from the 10 tosses:

The total number of heads divided by the total number of tosses is the relative frequency of heads. It is the proportion of the time that heads occurred on these tosses. The total number of tails divided by the total number of tosses is the relative frequency of tails.
a. Beth started to complete the following table as a way to investigate the relative frequencies. For each outcome, the total number of tosses increased. The total number of heads or tails observed so far depends on the outcome of the current toss. Complete this table for the 10 tosses recorded in the previous table.

b. What is the sum of the relative frequency of heads and the relative frequency of tails for each row of the table?
c. Beth’s results can also be displayed using a graph. Use the values of the relative frequency of heads so far from the table in part (a) to complete the graph below.

d. Beth continued tossing the coin and recording the results for a total of 40 tosses. Here are the results of the next 30 tosses:

As the number of tosses increases, the relative frequency of heads changes. Complete the following table for the 40 coin tosses:

e. Use the relative frequency of heads so far from the table in part (d) to complete the graph below for the total number of tosses of 1, 5, 10, 15, 20, 25, 30, 35, and 40.

f. What do you notice about the changes in the relative frequency of the number of heads so far as the number of tosses increases?
g. If you tossed the coin 100 times, what do you think the relative frequency of heads would be? Explain your answer.
h. Based on the graph and the relative frequencies, what would you estimate the probability of getting heads to be? Explain your answer.
i. How close is your estimate in part (h) to the theoretical probability of 0.5? Would the estimate of this probability have been as good if Beth had only tossed the coin a few times instead of 40?
The value you gave in part (h) is an estimate of the theoretical probability and is called an experimental or estimated probability.
Answer:
a.

b. The sum of the relative frequency of heads and the relative frequency of tails for each row is 1.00.

c.

d.

e.

f. The relative frequencies seem to change less as the number of tosses increases. The line drawn to connect the relative frequencies seems to be leveling off.

g. Answers will vary. Anticipate most students will indicate 50 heads result in 100 tosses, for a relative frequency of 0.50. This is a good time to indicate that the value of 0.50 is where the graph of the relative frequencies seems to be approaching. However, the relative frequencies will vary. For example, if the relative frequency for 100 tosses was 0.50 (and it could be), what would the relative frequency for 101 tosses be? Point out to students that no matter the outcome on the 101st toss, the relative frequency of heads would not be exactly 0.50.

h. Answers will vary. Anticipate that students will estimate the probability to be 0.50, as that is what they determined in the opening discussion, and that is the value that the relative frequencies appear to be approaching. Some students may estimate the probability as 0.48, as that was the last relative frequency obtained after 40 tosses. That estimate is also a good estimate of the probability.

i. In the beginning, the relative frequencies jump around. The estimated probabilities and the theoretical probabilities should be nearly the same as the number of observations increases. The estimated probabilities would likely not be as good after just a few coin tosses.

Eureka Math Grade 7 Module 5 Lesson 8 Exercise Answer Key

Exercises 1–8
Beth received nine more pennies. She securely taped them together to form a small stack. The top penny of her stack showed heads, and the bottom penny showed tails. If Beth tosses the stack, what outcomes could she observe?
Answer:
She could observe heads, tails, and on the side.

Exercise 1.
Beth wanted to determine the probability of getting heads when she tosses the stack. Do you think this probability is the same as the probability of getting heads with just one coin? Explain your answer.
Answer:
The outcomes when tossing this stack would be {heads, tails, side}. This changes the probability of getting heads, as there are three outcomes.

Exercise 2.
Make a sturdy stack of 10 pennies in which one end of the stack has a penny showing heads and the other end tails. Make sure the pennies are taped securely, or you may have a mess when you toss the stack. Toss the stack to observe possible outcomes. What is the sample space for tossing a stack of 10 pennies taped together? Do you think the probability of each outcome of the sample space is equal? Explain your answer.
Answer:
The sample space is {heads, tails, side}. A couple of tosses should clearly indicate to students that the stack often lands on its side. As a result, the probabilities of heads, tails, and on the side do not appear to be the same.

Exercise 3.
Record the results of 10 tosses. Complete the following table of the relative frequencies of heads for your 10 tosses:

Answer:
Answers will vary; the results of an actual toss are shown below.

Exercise 4.
Based on the value of the relative frequencies of heads so far, what would you estimate the probability of getting heads to be?
Answer:
If students had a sample similar to the above, they would estimate the probability of tossing a heads as 0.20 (or something close to that last relative frequency).

Exercise 5.
Toss the stack of 10 pennies another 20 times. Complete the following table:

Answer:
Answers will vary; student data will be different.

Exercise 6.
Summarize the relative frequency of heads so far by completing the following table:

Answer:
A sample table is provided using data from Exercises 3 and 5.

Exercise 7.
Based on the relative frequencies for the 30 tosses, what is your estimate of the probability of getting heads? Can you compare this estimate to a theoretical probability like you did in the first example? Explain your answer.
Answer:
Answers will vary. Students are anticipated to indicate an estimated probability equal or close to the last value in the relative frequency column. For this example, that would be 0.27. An estimate of 0.25 for this sample would have also been a good estimate. Students would indicate that they could not compare this to a theoretical probability because the theoretical probability is not known for this example. Allow for a range of estimated probabilities. Factors that might affect the results for the long-run frequencies include how much tape is used to create the stack and how sturdy the stack is. Discussing these points with students is a good summary of this lesson.

Exercise 8.
Create another stack of pennies. Consider creating a stack using 5 pennies, 15 pennies, or 20 pennies taped together in the same way you taped the pennies to form a stack of 10 pennies. Again, make sure the pennies are taped securely, or you might have a mess!
Toss the stack you made 30 times. Record the outcome for each toss:

Answer:
The Problem Set involves another example of obtaining results from a stack of pennies. Suggestions include stacks of 5, 15, and 20 (or a chosen number). The Problem Set includes questions based on the results from tossing one of these stacks. Provide students in small groups one of these stacks. Each group should collect data for 30 tosses to use for the Problem Set.

Eureka Math Grade 7 Module 5 Lesson 8 Problem Set Answer Key

Question 1.
If you created a stack of 15 pennies taped together, do you think the probability of getting a heads on a toss of the stack would be different than for a stack of 10 pennies? Explain your answer.
Answer:
The estimated probability of getting a heads for a stack of 15 pennies would be different than for a stack of 10 pennies. A few tosses indicate that it is very unlikely that the outcome of heads or tails would result, as the stack almost always lands on its side. (The possibility of a heads or a tails is noted, but it has a small probability of being observed.)

Question 2.
If you created a stack of 20 pennies taped together, what do you think the probability of getting a heads on a toss of the stack would be? Explain your answer.
Answer:
The estimated probability of getting a heads for a stack of 20 pennies is very small. The toss of a stack of this number of pennies almost always lands on its side.

Question 3.
Based on your work in this lesson, complete the following table of the relative frequencies of heads for the stack you created:

Answer:
Answers will vary based on the outcomes of tossing the stack. Anticipate results of 0 for a stack of 20 pennies. Samples involving 15 pennies have a very small probability of showing heads.

Question 4.
What is your estimate of the probability that your stack of pennies will land heads up when tossed? Explain your answer.
Answer:
Answers will vary based on the relative frequencies.

Question 5.
Is there a theoretical probability you could use to compare to the estimated probability? Explain your answer.
Answer:
There is no theoretical probability that could be calculated to compare to the estimated probability.

Eureka Math Grade 7 Module 5 Lesson 8 Exit Ticket Answer Key

Question 1.
Which of the following graphs would not represent the relative frequencies of heads when tossing 1 penny? Explain your answer.

Answer:
Graph A would not represent a possible graph of the relative frequencies. The first problem is the way Graph A starts. After the first toss, the probability would either be a 0 or a 1. Also, it seems to settle exactly to the theoretical probability without showing the slight changes from toss to toss.

Question 2.
Jerry indicated that after tossing a penny 30 times, the relative frequency of heads was 0.47 (to the nearest hundredth). He indicated that after 31 times, the relative frequency of heads was 0.55. Are Jerry’s summaries correct? Why or why not?
Answer:
Jerry’s summaries have errors. If he tossed the penny 30 times and the relative frequency of heads was 0.47, then he had 14 heads. If his next toss was heads, then the relative frequency would be \(\frac{15}{31}\), or 0.48 (to the nearest hundredth). If his next toss was tails, then the relative frequency would be \(\frac{14}{31}\), or 0.45 (to the nearest hundredth).

Question 3.
Jerry observed 5 heads in 100 tosses of his coin. Do you think this was a fair coin? Why or why not?
Answer:
Students should indicate Jerry’s coin is probably not a fair coin. The relative frequency of heads for a rather large number of tosses should be close to the theoretical probability. For this problem, the relative frequency of 0.05 is quite different from 0.5 and probably indicates that the coin is not fair.

Engage NY Eureka Math 7th Grade Module 5 Lesson 7 Answer Key

Eureka Math Grade 7 Module 5 Lesson 7 Example Answer Key

Example 1: Three Nights of Games
Recall a previous example where a family decides to play a game each night, and they all agree to use a tetrahedral die (a four-sided die in the shape of a pyramid where each of four possible outcomes is equally likely) each night to randomly determine if the game will be a board (B) or a card (C) game. The tree diagram mapping the possible overall outcomes over two consecutive nights was as follows:

But how would the diagram change if you were interested in mapping the possible overall outcomes over three consecutive nights? To accommodate this additional third stage, you would take steps similar to what you did before. You would attach all possibilities for the third stage (Wednesday) to each branch of the previous stage (Tuesday).

Answer:
Read through the example in the student lesson as a class. Convey the following important points about the tree diagram for this example:
 The tree diagram is an important way of organizing and visualizing outcomes.
 The tree diagram is particularly useful when the experiment can be thought of as occurring in stages.
 When the information about probabilities associated with each branch is included, the tree diagram facilitates the computation of the probabilities of possible outcomes.
 The basic principles of tree diagrams can apply to situations with more than two stages.

Example 2: Three Nights of Games (with Probabilities)
In Example 1, each night’s outcome is the result of a chance experiment (rolling the four-sided die). Thus, there is a probability associated with each night’s outcome.

By multiplying the probabilities of the outcomes from each stage, you can obtain the probability for each “branch of the tree.” In this case, you can figure out the probability of each of our eight outcomes.

For this family, a card game will be played if the die lands showing a value of 1, and a board game will be played if the die lands showing a value of 2, 3, or 4. This makes the probability of a board game (B) on a given night 0.75.
Let’s use a tree to examine the probabilities of the outcomes for the three days.

Answer:
Ask students:
→ What does CBC represent?
CBC represents the following sequence: card game the first night, board game the second night, and card game the third night.

→ The probability of CBC is approximately 0.046785. What does this probability mean?
The probability of CBC is very small. This means that the outcome of CBC is not expected to happen very often.

Eureka Math Grade 7 Module 5 Lesson 7 Exercise Answer Key

Exercises 1 – 3
Exercise 1.
If BBB represents three straight nights of board games, what does CBB represent?
Answer:
CBB would represent a card game on the first night and a board game on each of the second and third nights.

Exercise 2.
List all outcomes where exactly two board games were played over three days. How many outcomes were there?
Answer:
BBC, BCB, and CBB—there are 3 outcomes.

Exercise 3.
There are eight possible outcomes representing the three nights. Are the eight outcomes representing the three nights equally likely? Why or why not?
Answer:
As in the exercises of the previous lesson, the probability of C and B are not the same. As a result, the probability of the outcome CCC (all three nights involve card games) is not the same as BBB (all three nights playing board games). The probability of playing cards was only \(\frac{1}{4}\) in the previous lesson.

Exercises 4 – 6
Exercise 4.
Probabilities for two of the eight outcomes are shown. Calculate the approximate probabilities for the remaining six outcomes.
Answer:
BBC: 0.75(0.75)(0.25) = 0.140625
BCB: 0.75(0.25)(0.75) = 0.140625
BCC: 0.75(0.25)(0.25) = 0.046875
CBB: 0.25(0.75)(0.75) = 0.140625
CCB: 0.25(0.25)(0.75) = 0.046875
CCC: 0.25(0.25)(0.25) = 0.015625

Exercise 5.
What is the probability that there will be exactly two nights of board games over the three nights?
Answer:
The three outcomes that contain exactly two nights of board games are BBC, BCB, and CBB. The probability of exactly two nights of board games would be the sum of the probabilities of these outcomes, or
0.140625 + 0.140625 + 0.140625 = 0.421875.

Exercise 6.
What is the probability that the family will play at least one night of card games?
Answer:
This “at least” question could be answered by subtracting the probability of no card games (BBB) from 1. When you remove the BBB from the list of eight outcomes, the remaining outcomes include at least one night of card games. The probability of three nights of board games (BBB) is 0.421875. Therefore, the probability of at least one night of card games would be the probability of all outcomes (or 1) minus the probability of all board games, or
1 – 0.421875 = 0.578125.

Exercises 7 – 10: Three Children
A neighboring family just welcomed their third child. It turns out that all 3 of the children in this family are girls, and they are not twins or triplets. Suppose that for each birth, the probability of a boy birth is 0.5, and the probability of a girl birth is also 0.5. What are the chances of having 3 girls in a family’s first 3 births?

Exercise 7.
Draw a tree diagram showing the eight possible birth outcomes for a family with 3 children (no twins or triplets). Use the symbol B for the outcome of boy and G for the outcome of girl. Consider the first birth to be the first stage. (Refer to Example 1 if you need help getting started.)
Answer:

Exercise 8.
Write in the probabilities of each stage’s outcomes in the tree diagram you developed above, and determine the probabilities for each of the eight possible birth outcomes for a family with 3 children (no twins or triplets).
Answer:
In this case, since the probability of a boy is 0.5 and the probability of a girl is 0.5, each of the eight outcomes will have a probability of 0.125 of occurring.

Exercise 9.
What is the probability of a family having 3 girls in this situation? Is that greater than or less than the probability of having exactly 2 girls in 3 births?
Answer:
The probability of a family having 3 girls is 0.125. This is less than the probability of having exactly 2 girls in 3 births, which is 0.375 (the sum of the probabilities of GGB, GBG, and BGG). Note to teachers: Another way of explaining this to students is to point out that the probability of each outcome is the same, or 0.125. Therefore, the probability of 3 girls in 3 births is the probability of just one possible outcome. The probability of having exactly 2 girls in 3 births is the sum of the probabilities of three outcomes. Therefore, the probability of one of the outcomes is less than the probability of the sum of three outcomes (and again, emphasize that the probability of each outcome is the same).

Exercise 10.
What is the probability of a family of 3 children having at least 1 girl?
Answer:
The probability of having at least 1 girl would be found by subtracting the probability of no girls (or all boys, BBB) from 1, or 1-0.125 = 0.875.

Eureka Math Grade 7 Module 5 Lesson 7 Problem Set Answer Key

Question 1.
According to the Washington, D.C. Lottery’s website for its Cherry Blossom Double instant scratch game, the chance of winning a prize on a given ticket is about 17%. Imagine that a person stops at a convenience store on the way home from work every Monday, Tuesday, and Wednesday to buy a scratcher ticket and plays the game.
(Source: http://dclottery.com/games/scratchers/1223/cherry-blossom-doubler.aspx, accessed May 27, 2013)

a. Develop a tree diagram showing the eight possible outcomes of playing over these three days. Call stage one “Monday,” and use the symbols W for a winning ticket and L for a non-winning ticket.
b. What is the probability that the player will not win on Monday but will win on Tuesday and Wednesday?
c. What is the probability that the player will win at least once during the 3-day period?
Answer:
a.

b. LWW outcome: 0.83(0.17)(0.17)≈0.024
c. “Winning at least once” would include all outcomes except LLL (which has a probability of approximately 0.5718). The probabilities of these outcomes would sum to about 0.4282.
This is also equal to 1-0.5718.

Question 2.
A survey company is interested in conducting a statewide poll prior to an upcoming election. They are only interested in talking to registered voters.

Imagine that 55% of the registered voters in the state are male and 45% are female. Also, consider that the distribution of ages may be different for each group. In this state, 30% of male registered voters are age 18 – 24, 37% are age 25 – 64, and 33% are 65 or older. 32% of female registered voters are age 18 – 24, 26% are age 25 – 64, and 42% are 65 or older.

The following tree diagram describes the distribution of registered voters. The probability of selecting a male registered voter age 18 – 24 is 0.165.

a. What is the chance that the polling company will select a registered female voter age 65 or older?
b. What is the chance that the polling company will select any registered voter age 18 – 24?
Answer:
a. Female 65 or older: (0.45)(0.42) = 0.189
b. The probability of selecting any registered voter age 18 – 24 would be the sum of the probability of selecting a male registered voter age 18 – 24 and the probability of selecting a female registered voter age 18 – 24.
(0.55)(0.30) = 0.165
(0.45)(0.32) = 0.144
0.165 + 0.144 = 0.309
The probability of selecting any voter age 18 – 24 is 0.309.

Eureka Math Grade 7 Module 5 Lesson 7 Exit Ticket Answer Key

In a laboratory experiment, three mice will be placed in a simple maze that has just one decision point where a mouse can turn either left (L) or right (R). When the first mouse arrives at the decision point, the direction he chooses is recorded. The same is done for the second and the third mouse.
Question 1.
Draw a tree diagram where the first stage represents the decision made by the first mouse, the second stage represents the decision made by the second mouse, and so on. Determine all eight possible outcomes of the decisions for the three mice.
Answer:

Question 2.
Use the tree diagram from Problem 1 to help answer the following question. If, for each mouse, the probability of turning left is 0.5 and the probability of turning right is 0.5, what is the probability that only one of the three mice will turn left?
Answer:
There are three outcomes that have exactly one mouse turning left: LRR, RLR, and RRL. Each has a probability of 0.125, so the probability of having only one of the three mice turn left is 0.375.

Question 3.
If the researchers conducting the experiment add food in the simple maze such that the probability of each mouse turning left is now 0.7, what is the probability that only one of the three mice will turn left? To answer the question, use the tree diagram from Problem 1.
Answer:
As in Problem 2, there are three outcomes that have exactly one mouse turning left: LRR, RLR, and RRL. However, with the adjustment made by the researcher, each of the three outcomes now has a probability of 0.063. So now, the probability of having only one of the three mice turn left is the sum of three equally likely outcomes of 0.063, or 0.063(3) = 0.189. The tree provides a way to organize the outcomes and the probabilities.

Engage NY Eureka Math 7th Grade Module 5 Lesson 6 Answer Key

Eureka Math Grade 7 Module 5 Lesson 6 Example Answer Key

Example 1: Two Nights of Games
Imagine that a family decides to play a game each night. They all agree to use a tetrahedral die (i.e., a four-sided pyramidal die where each of four possible outcomes is equally likely—see the image at the end of this lesson) each night to randomly determine if they will play a board game (B) or a card game (C). The tree diagram mapping the possible overall outcomes over two consecutive nights will be developed below.
To make a tree diagram, first present all possibilities for the first stage (in this case, Monday).

Then, from each branch of the first stage, attach all possibilities for the second stage (Tuesday).

Note: If the situation has more than two stages, this process would be repeated until all stages have been presented.
a. If BB represents two straight nights of board games, what does CB represent?
b. List the outcomes where exactly one board game is played over two days. How many outcomes were there?
Answer:
a. CB would represent a card game on the first night and a board game on the second night.
b. BC and CB—there are two outcomes.

Example 2: Two Nights of Games (with Probabilities)
In Example 1, each night’s outcome is the result of a chance experiment (rolling the tetrahedral die). Thus, there is a probability associated with each night’s outcome.
By multiplying the probabilities of the outcomes from each stage, we can obtain the probability for each “branch of the tree.” In this case, we can figure out the probability of each of our four outcomes: BB, BC, CB, and CC.
For this family, a card game will be played if the die lands showing a value of 1, and a board game will be played if the die lands showing a value of 2, 3, or 4. This makes the probability of a board game (B) on a given night 0.75.

a. The probabilities for two of the four outcomes are shown. Now, compute the probabilities for the two remaining outcomes.
b. What is the probability that there will be exactly one night of board games over the two nights?
Answer:
a. CB: (0.25)(0.75) = 0.1875
CC: (0.25)(0.25) = 0.0625

b. The two outcomes that contain exactly one night of board games are BC and CB. The probability of exactly one night of board games would be the sum of the probabilities of these outcomes (since the outcomes are disjoint). 0.1875 + 0.1875 = 0.375 (Note: Disjoint means two events that cannot both happen at once.)

Eureka Math Grade 7 Module 5 Lesson 6 Exercise Answer Key

Two friends meet at a grocery store and remark that a neighboring family just welcomed their second child. It turns out that both children in this family are girls, and they are not twins. One of the friends is curious about what the chances are of having 2 girls in a family’s first 2 births. Suppose that for each birth, the probability of a boy birth is 0.5 and the probability of a girl birth is also 0.5.

Exercise 1.
Draw a tree diagram demonstrating the four possible birth outcomes for a family with 2 children (no twins). Use the symbol B for the outcome of boy and G for the outcome of girl. Consider the first birth to be the first stage. (Refer to Example 1 if you need help getting started.)
Answer:

Exercise 2.
Write in the probabilities of each stage’s outcome to the tree diagram you developed above, and determine the probabilities for each of the 4 possible birth outcomes for a family with 2 children (no twins).
Answer:
In this case, since the probability of a boy is 0.5 and the probability of a girl is 0.5, each of the four outcomes will have a 0.25 probability of occurring because (0.5)(0.5) = 0.25.

Exercise 3.
What is the probability of a family having 2 girls in this situation? Is that greater than or less than the probability of having exactly 1 girl in 2 births?
Answer:
The probability of a family having 2 girls is 0.25. This is less than the probability of having exactly 1 girl in 2 births, which is 0.5 (the sum of the probabilities of BG and GB).

Eureka Math Grade 7 Module 5 Lesson 6 Problem Set Answer Key

Question 1.
Imagine that a family of three (Alice, Bill, and Chester) plays bingo at home every night. Each night, the chance that any one of the three players will win is \(\frac{1}{3}\).
a. Using A for Alice wins, B for Bill wins, and C for Chester wins, develop a tree diagram that shows the nine possible outcomes for two consecutive nights of play.
b. Is the probability that “Bill wins both nights” the same as the probability that “Alice wins the first night and Chester wins the second night”? Explain.
Answer:
a.

b. Yes. The probability of Bill winning both nights is \(\frac{1}{3}\) ∙ \(\frac{1}{3}\) = \(\frac{1}{9}\), which is the same as the probability of Alice winning the first night and Chester winning the second night (\(\frac{1}{3}\)∙\(\frac{1}{3}\) = \(\frac{1}{9}\)).

Question 2.
According to the Washington, D.C. Lottery’s website for its Cherry Blossom Doubler instant scratch game, the chance of winning a prize on a given ticket is about 17%. Imagine that a person stops at a convenience store on the way home from work every Monday and Tuesday to buy a scratcher ticket to play the game.
(Source: http://dclottery.com/games/scratchers/1223/cherry-blossom-doubler.aspx, accessed May 27, 2013)

a. Develop a tree diagram showing the four possible outcomes of playing over these two days. Call stage 1 “Monday,” and use the symbols W for a winning ticket and L for a non-winning ticket.
b. What is the chance that the player will not win on Monday but will win on Tuesday?
c. What is the chance that the player will win at least once during the two-day period?
Answer:
a.

b. LW outcome: (0.83)(0.17) = 0.1411
c. “Winning at least once” would include all outcomes except LL (which has a 0.6889 probability). The probabilities of these outcomes would sum to 0.3111.

Image of Tetrahedral Die
Source: http://commons.wikimedia.org/wiki/File:4-sided_dice_250.jpg
Photo by Fantasy, via Wikimedia Commons, is licensed under CC BY-SA 3.0,
http://creativecommons.org/licenses/by-sa/3.0/deed.en.

Eureka Math Grade 7 Module 5 Lesson 6 Exit Ticket Answer Key

In a laboratory experiment, two mice will be placed in a simple maze with one decision point where a mouse can turn either left (L) or right (R). When the first mouse arrives at the decision point, the direction it chooses is recorded. Then, the process is repeated for the second mouse.
Question 1.
Draw a tree diagram where the first stage represents the decision made by the first mouse and the second stage represents the decision made by the second mouse. Determine all four possible decision outcomes for the two mice.
Answer:

Question 2.
If the probability of turning left is 0.5 and the probability of turning right is 0.5 for each mouse, what is the probability that only one of the two mice will turn left?
Answer:
There are two outcomes that have exactly one mouse turning left: LR and RL. Each has a probability of 0.25, so the probability of only one of the two mice turning left is 0.25 + 0.25 = 0.5.

Question 3.
If the researchers add food in the simple maze such that the probability of each mouse turning left is now 0.7, what is the probability that only one of the two mice will turn left?
Answer:

As in Problem 2, there are two outcomes that have exactly one mouse turning left: LR and RL. However, with the adjustment made by the researcher, each of these outcomes now has a probability of 0.21. So now, the probability of only one of the two mice turning left is 0.21 + 0.21 = 0.42.

Engage NY Eureka Math 7th Grade Module 5 Lesson 5 Answer Key

Eureka Math Grade 7 Module 5 Lesson 5 Example Answer Key

Example 1.
When Jenna goes to the farmers’ market, she usually buys bananas. The number of bananas she might buy and their probabilities are shown in the table below.

a. What is the probability that Jenna buys exactly 3 bananas?
b. What is the probability that Jenna does not buy any bananas?
c. What is the probability that Jenna buys more than 3 bananas?
d. What is the probability that Jenna buys at least 3 bananas?
e. What is the probability that Jenna does not buy exactly 3 bananas?
Notice that the sum of the probabilities in the table is one whole (0.1 + 0.1 + 0.1 + 0.2 + 0.2 + 0.3 = 1). This is always true; when we add up the probabilities of all the possible outcomes, the result is always 1. So, taking 1 and subtracting the probability of the event gives us the probability of something not occurring.
Answer:
a. You can see from the table that the probability that Jenna buys exactly 3 bananas is 0.2, or 20%.
b. The probability that Jenna buys 0 bananas is 0.1, or 10%.
c. The probability that Jenna buys 4 or 5 bananas is 0.2 + 0.3 = 0.5, or 50%.
d. The probability that Jenna buys 3, 4, or 5 bananas is 0.2 + 0.2 + 0.3 = 0.7, or 70%.
e. Remember that the probability that an event does not happen is
1-(the probability that the event does happen).
So, the probability that Jenna does not buy exactly 3 bananas is
1-(the probability that she does buy exactly 3 bananas)
1-0.2 = 0.8, or 80%.

Example 2.
Luis works in an office, and the phone rings occasionally. The possible number of phone calls he receives in an afternoon and their probabilities are given in the table below.

a. Find the probability that Luis receives 3 or 4 phone calls.
b. Find the probability that Luis receives fewer than 2 phone calls.
c. Find the probability that Luis receives 2 or fewer phone calls.
d. Find the probability that Luis does not receive 4 phone calls.
Answer:
a. The probability that Luis receives 3 or 4 phone calls is \(\frac{1}{3}\) + \(\frac{1}{9}\) = \(\frac{3}{9}\) + \(\frac{1}{9}\) = \(\frac{4}{9}\).
b. The probability that Luis receives fewer than 2 phone calls is \(\frac{1}{6}\) + \(\frac{1}{6}\) = \(\frac{2}{6}\) = \(\frac{1}{3}\).
c. The probability that Luis receives 2 or fewer phone calls is \(\frac{2}{9}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) = \(\frac{4}{18}\) + \(\frac{3}{18}\) + \(\frac{3}{18}\) = \(\frac{10}{18}\) = \(\frac{5}{9}\).
d. The probability that Luis does not receive 4 phone calls is 1-\(\frac{1}{9}\) = \(\frac{9}{9}\)–\(\frac{1}{9}\) = \(\frac{8}{9}\).

If there is time available, ask students:
How would you calculate the probability that Luis receives at least one call? What might be a quicker way of doing this?
→ I would add the probabilities for 1, 2, 3, and 4:
\(\frac{1}{6} + \frac{2}{9} + \frac{1}{3} + \frac{1}{9}\) = \(\frac{3}{18} + \frac{4}{18} + \frac{2}{18}\) = \(\frac{15}{18}\) = \(\frac{5}{6}\)
→ The quicker way is to say that the probability he gets at least one call is the probability that he does not get zero calls, and so the required probability is 1-\(\frac{1}{6}\) = \(\frac{5}{6}\).

Eureka Math Grade 7 Module 5 Lesson 5 Exercise Answer Key

Exercises 1–2
Jenna’s husband, Rick, is concerned about his diet. On any given day, he eats 0, 1, 2, 3, or 4 servings of fruits and vegetables. The probabilities are given in the table below.

Exercise 1.
1. On a given day, find the probability that Rick eats
a. Two servings of fruits and vegetables
b. More than two servings of fruits and vegetables
c. At least two servings of fruits and vegetables
Answer:
a. 0.28
b. 0.39 + 0.12 = 0.51
c. 0.28 + 0.39 + 0.12 = 0.79

Exercise 2.
Find the probability that Rick does not eat exactly two servings of fruits and vegetables.
Answer:
1-0.28 = 0.72

Exercises 3–7
When Jenna goes to the farmers’ market, she also usually buys some broccoli. The possible number of heads of broccoli that she buys and the probabilities are given in the table below.

Exercise 3.
Find the probability that Jenna:
a. Buys exactly 3 heads of broccoli
b. Does not buy exactly 3 heads of broccoli
c. Buys more than 1 head of broccoli
d. Buys at least 3 heads of broccoli
Answer:
a. \(\frac{1}{4}\)
b. 1-\(\frac{1}{4}\) = \(\frac{3}{4}\)
c. \(\frac{5}{12}\) + \(\frac{1}{4}\) + \(\frac{1}{12}\) = \(\frac{3}{4}\)
d. \(\frac{1}{4}\) + \(\frac{1}{12}\) = \(\frac{1}{3}\)

The diagram below shows a spinner designed like the face of a clock. The sectors of the spinner are colored red (R), blue (B), green (G), and yellow (Y).

Exercise 4.
Writing your answers as fractions in lowest terms, find the probability that the pointer stops on the following colors.
a. Red:
b. Blue:
c. Green:
d. Yellow:
Answer:
a. Red: \(\frac{1}{12}\)
b. Blue: \(\frac{2}{12}\) = \(\frac{1}{6}\)
c. Green: \(\frac{5}{12}\)
d. Yellow: \(\frac{4}{12}\) = \(\frac{1}{3}\)

Exercise 5.
Complete the table of probabilities below.

Answer:

Exercise 6.
Find the probability that the pointer stops in either the blue region or the green region.
Answer:
\(\frac{1}{6}\) + \(\frac{5}{12}\) = \(\frac{7}{12}\)

Exercise 7.
Find the probability that the pointer does not stop in the green region.
Answer:
1-\(\frac{5}{12}\) = \(\frac{7}{12}\)

Eureka Math Grade 7 Module 5 Lesson 5 Problem Set Answer Key

Question 1.
The Gator Girls is a soccer team. The possible number of goals the Gator Girls will score in a game and their probabilities are shown in the table below.

Find the probability that the Gator Girls:
a. Score more than two goals
b. Score at least two goals
c. Do not score exactly 3 goals
Answer:
a. 0.11 + 0.03 = 0.14
b. 0.33 + 0.11 + 0.03 = 0.47
c. 1-0.11 = 0.89

Question 2.
The diagram below shows a spinner. The pointer is spun, and the player is awarded a prize according to the color on which the pointer stops.

a. What is the probability that the pointer stops in the red region?
b. Complete the table below showing the probabilities of the three possible results.

c. Find the probability that the pointer stops on green or blue.
d. Find the probability that the pointer does not stop on green.
Answer:
a. \(\frac{1}{2}\)
b.
c. \(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{1}{2}\)
d. 1-\(\frac{1}{4}\) = \(\frac{3}{4}\)

Question 3.
Wayne asked every student in his class how many siblings (brothers and sisters) they had. The survey results are shown in the table below. (Wayne included himself in the results.)

(Note: The table tells us that 4 students had no siblings, 5 students had one sibling, 14 students had two siblings, and so on.)
a. How many students are there in Wayne’s class, including Wayne?
b. What is the probability that a randomly selected student does not have any siblings? Write your answer as a fraction in lowest terms.
c. The table below shows the possible number of siblings and the probabilities of each number. Complete the table by writing the probabilities as fractions in lowest terms.

d. Writing your answers as fractions in lowest terms, find the probability that the student:
i. Has fewer than two siblings
ii. Has two or fewer siblings
iii. Does not have exactly one sibling
Answer:
a. 4 + 5 + 14 + 6 + 3 = 32
b. \(\frac{4}{32}\) = \(\frac{1}{8}\)
c.

d. i) \(\frac{1}{8} + \frac{5}{32}\) = \(\frac{9}{32}\)
ii) \(\frac{1}{8} + \frac{5}{32} + \frac{7}{16}\) = \(\frac{23}{32}\)
iii) 1-\(\frac{5}{32}\) = \(\frac{27}{32}\)

Eureka Math Grade 7 Module 5 Lesson 5 Exit Ticket Answer Key

Carol is sitting on the bus on the way home from school and is thinking about the fact that she has three homework assignments to do tonight. The table below shows her estimated probabilities of completing 0, 1, 2, or all 3 of the assignments.

Question 1.
Writing your answers as fractions in lowest terms, find the probability that Carol completes
a. Exactly one assignment
b. More than one assignment
c. At least one assignment
Answer:
a. \(\frac{2}{9}\)
b. \(\frac{5}{18} + \frac{1}{3}\) = \(\frac{5}{18} + \frac{6}{18}\) = \(\frac{11}{18}\)
c. \(\frac{2}{9} + \frac{5}{18} + \frac{1}{3}\) = \(\frac{4}{18} + \frac{5}{18} + \frac{6}{18}\) = \(\frac{15}{18}\) = \(\frac{5}{6}\)

Question 2.
Find the probability that the number of homework assignments Carol completes is not exactly 2.
Answer:
1-\(\frac{5}{18}\) = \(\frac{13}{18}\)

Question 3.
Carol has a bag containing 3 red chips, 10 blue chips, and 7 green chips. Estimate the probability (as a fraction or decimal) of Carol reaching into her bag and pulling out a green chip.
Answer:
An estimate of the probability would be 7 out of 20, \(\frac{7}{20}\), or 0.35.

Engage NY Eureka Math 7th Grade Module 5 Lesson 4 Answer Key

Eureka Math Grade 7 Module 5 Lesson 4 Example Answer Key

Examples: Theoretical Probability
In a previous lesson, you saw that to find an estimate of the probability of an event for a chance experiment you divide
P(event) = \(\frac{\text { Number of observed occurrences of the event }}{\text { Total number of observations }}\)
Your teacher has a bag with some cubes colored yellow, green, blue, and red. The cubes are identical except for their color. Your teacher will conduct a chance experiment by randomly drawing a cube with replacement from the bag. Record the outcome of each draw in the table below.

Answer:

Example 1.
Based on the 20 trials, estimate for the probability of
a. Choosing a yellow cube
b. Choosing a green cube
c. Choosing a red cube
d. Choosing a blue cube
Answer:
a. Answers will vary but should be approximately \(\frac{5}{20}\), or \(\frac{1}{4}\). The probability in the sample provided is \(\frac{5}{20}\), or \(\frac{1}{4}\) .

b. Answers will vary but should be approximately \(\frac{5}{20}\), or \(\frac{1}{4}\). The probability in the sample provided is \(\frac{6}{20}\), or \(\frac{3}{10}\).

c. Answers will vary but should be approximately \(\frac{5}{20}\), or \(\frac{1}{4}\). The probability in the sample provided is \(\frac{4}{20}\), or \(\frac{1}{5}\).

d. Answers will vary but should be approximately \(\frac{5}{20}\), or \(\frac{1}{4}\). The probability in the sample provided is \(\frac{5}{20}\), or \(\frac{1}{4}\).

Example 2.
If there are 40 cubes in the bag, how many cubes of each color are in the bag? Explain.
Answer:
Answers will vary. Because the estimated probabilities are about the same for each color, we can predict that there are approximately the same number of each color of cube in the bag. Since an equal number of each color is estimated, approximately 10 of each color are predicted.

Example 3.
If your teacher were to randomly draw another 20 cubes one at a time and with replacement from the bag, would you see exactly the same results? Explain.
Answer:
No. This is an example of a chance experiment, so the results will vary.

Example 4.
Find the fraction of each color of cubes in the bag.
Yellow
Green
Red
Blue
Answer:
Yellow \(\frac{10}{40}\), or \(\frac{1}{4}\)
Green \(\frac{10}{40}\), or \(\frac{1}{4}\)
Red \(\frac{10}{40}\), or \(\frac{1}{4}\)
Blue \(\frac{10}{40}\), or \(\frac{1}{4}\)
Present the formal definition of the theoretical probability of an outcome when outcomes are equally likely. Then, ask
→ Why is the numerator of the fraction just 1?
Since the outcomes are equally likely, each one of the outcomes is just as likely as the other.
Define the word event as “a collection of outcomes.” Then, present that definition to students, and ask

→ Why is the numerator of the fraction not always 1?
Since there is a collection of outcomes, there may be more than one favorable outcome.
Use the cube example to explain the difference between an outcome and an event. Explain that each cube is equally likely to be chosen (an outcome), while the probability of drawing a blue cube (an event) is \(\frac{10}{40}\).

Each fraction is the theoretical probability of choosing a particular color of cube when a cube is randomly drawn from the bag.
When all the possible outcomes of an experiment are equally likely, the probability of each outcome is
P(outcome) = \(\frac{1}{\text { Number of possible outcomes }}\)

An event is a collection of outcomes, and when the outcomes are equally likely, the theoretical probability of an event can be expressed as
P(event) = \(\frac{\text { Number of favorable outcomes }}{\text { Number of possible outcomes }}\).

The theoretical probability of drawing a blue cube is
P(blue) = \(\frac{\text { Number of blue cubes }}{\text { Total number of cubes }}\) = \(\frac{10}{40}\).
Answer:

Example 5.
Is each color equally likely to be chosen? Explain your answer.
Answer:
Yes. There are the same numbers of cubes for each color.

Example 6.
How do the theoretical probabilities of choosing each color from Exercise 4 compare to the experimental probabilities you found in Exercise 1?
Answer:
Answers will vary.

Example 7.
An experiment consisted of flipping a nickel and a dime. The first step in finding the theoretical probability of obtaining a heads on the nickel and a heads on the dime is to list the sample space. For this experiment, complete the sample space below.
Nickel Dime
What is the probability of flipping two heads?
Answer:

If the coins are fair, these outcomes are equally likely, so the probability of each outcome is \(\frac{1}{4}\).

The probability of two heads is \(\frac{1}{4}\) or P(two heads) = \(\frac{1}{4}\).

Eureka Math Grade 7 Module 5 Lesson 4 Exercise Answer Key

Exercises 1–4
Exercise 1.
Consider a chance experiment of rolling a six-sided number cube with the numbers 1–6 on the faces.
a. What is the sample space? List the probability of each outcome in the sample space.
b. What is the probability of rolling an odd number?
c. What is the probability of rolling a number less than 5?
Answer:
a. Sample space: 1, 2, 3, 4, 5, 6
Probability of each outcome is \(\frac{1}{6}\).

b. \(\frac{3}{6}\), or \(\frac{1}{2}\)

c. \(\frac{4}{6}\), or \(\frac{2}{3}\)

Exercise 2.
Consider an experiment of randomly selecting a letter from the word number.
a. What is the sample space? List the probability of each outcome in the sample space.
b. What is the probability of selecting a vowel?
c. What is the probability of selecting the letter z?
Answer:
a. Sample space: n, u, m, b, e, r
Probability of each outcome is \(\frac{1}{6}\).

b. \(\frac{2}{6}\), or \(\frac{1}{3}\)

c. \(\frac{0}{6}\), or 0

Exercise 3.
Consider an experiment of randomly selecting a square from a bag of 10 squares.
a. Color the squares below so that the probability of selecting a blue square is \(\frac{1}{2}\).

b. Color the squares below so that the probability of selecting a blue square is \(\frac{4}{5}\).

Answer:
a. Five squares should be colored blue.
b. Eight squares should be colored blue.

Exercise 4.
Students are playing a game that requires spinning the two spinners shown below. A student wins the game if both spins land on red. What is the probability of winning the game? Remember to first list the sample space and the probability of each outcome in the sample space. There are eight possible outcomes to this chance experiment.

Answer:
Sample space: R1 R2, R1 B2, R1 G2, R1 Y2, B1 R2, B1 B2, B1 G2, B1 Y2
Each outcome has a probability of \(\frac{1}{8}\).
Probability of a win (both red) is\(\frac{1}{8}\).

Eureka Math Grade 7 Module 5 Lesson 4 Problem Set Answer Key

Question 1.
In a seventh-grade class of 28 students, there are 16 girls and 12 boys. If one student is randomly chosen to win a prize, what is the probability that a girl is chosen?
Answer:
\(\frac{16}{28}\), or \(\frac{4}{7}\)

Question 2.
An experiment consists of spinning the spinner once.

a. Find the probability of landing on a 2.
b. Find the probability of landing on a 1.
c. Is landing in each section of the spinner equally likely to occur? Explain.
Answer:
a. \(\frac{2}{8}\), or \(\frac{1}{4}\)
b. \(\frac{3}{8}\)
c. Yes. Each section is the same size.

Question 3.
An experiment consists of randomly picking a square section from the board shown below.

a. Find the probability of choosing a triangle.
b. Find the probability of choosing a star.
c. Find the probability of choosing an empty square.
d. Find the probability of choosing a circle.
Answer:
a. \(\frac{8}{16}\), or \(\frac{1}{2}\)
b. \(\frac{4}{16}\), or \(\frac{1}{4}\)
c. \(\frac{4}{16}\), or \(\frac{1}{4}\)
d. \(\frac{0}{16}\), or 0

Question 4.
Seventh graders are playing a game where they randomly select two integers 0–9, inclusive, to form a two-digit number. The same integer might be selected twice.
a. List the sample space for this chance experiment. List the probability of each outcome in the sample space.
b. What is the probability that the number formed is between 90 and 99, inclusive?
c. What is the probability that the number formed is evenly divisible by 5?
d. What is the probability that the number formed is a factor of 64?
Answer:
a. Sample space: Numbers 00–99 Probability of each outcome is \(\frac{1}{100}\).
b. \(\frac{10}{100}\), or \(\frac{1}{10}\)
c. \(\frac{20}{100}\), or \(\frac{1}{5}\)
d. \(\frac{7}{100}\) (Factors of 64 are 1, 2, 4, 8, 16, 32, and 64.)

Question 5.
A chance experiment consists of flipping a coin and rolling a number cube with the numbers 1–6 on the faces of the cube.
a. List the sample space of this chance experiment. List the probability of each outcome in the sample space.
b. What is the probability of getting a heads on the coin and the number 3 on the number cube?
c. What is the probability of getting a tails on the coin and an even number on the number cube?
Answer:
a. Sample space: H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6 The probability of each outcome is \(\frac{1}{12}\).
b. \(\frac{1}{12}\)
c. \(\frac{3}{12}\), or \(\frac{1}{4}\)

Question 6.
A chance experiment consists of spinning the two spinners below.

a. List the sample space and the probability of each outcome.
b. Find the probability of the event of getting a red on the first spinner and a red on the second spinner.
c. Find the probability of a red on at least one of the spinners.
Answer:
a. Sample space: R1 R2, R1 G2, R1 Y2, B1 R2, B1 G2, B1 Y2 Each outcome has a probability of \(\frac{1}{6}\).
b. \(\frac{1}{6}\)
c. \(\frac{4}{6}\), or \(\frac{2}{3}\)

Eureka Math Grade 7 Module 5 Lesson 4 Exit Ticket Answer Key

An experiment consists of randomly drawing a cube from a bag containing three red and two blue cubes.
Question 1.
What is the sample space of this experiment?
Answer:
Red, blue

Question 2.
List the probability of each outcome in the sample space.
Answer:
Probability of red is \(\frac{3}{5}\). Probability of blue is \(\frac{2}{5}\).

Question 3.
Is the probability of selecting a red cube equal to the probability of selecting a blue cube? Explain.
Answer:
No. There are more red cubes than blue cubes, so red has a greater probability of being chosen.

Engage NY Eureka Math 7th Grade Module 5 Lesson 1 Answer Key

Eureka Math Grade 7 Module 5 Lesson 1 Example Answer Key

Example 1: Spinner Game
Suppose you and your friend are about to play a game using the spinner shown here:

Rules of the game:
1. Decide who will go first.
2. Each person picks a color. Both players cannot pick the same color.
3. Each person takes a turn spinning the spinner and recording what color the spinner stops on. The winner is the person whose color is the first to happen 10 times.
Play the game, and remember to record the color the spinner stops on for each spin.
Answer:
Students try their spinners a few times before starting the game. Before students begin to play the game, discuss who should go first. Consider, for example, having the person born earliest in the year go first. If it is a tie, consider another option like tossing a coin. Discuss with students the following questions:
→ Will it make a difference who goes first?
The game is designed so that the spinner landing on green is more likely to occur. Therefore, if the first person selects green, this person has an advantage.

→ Who do you think will win the game?
The person selecting green has an advantage.

→ Do you think this game is fair?
No. The spinner is designed so that green will occur more often. As a result, the student who selects green will have an advantage.

→ Play the game, and remember to record the color the spinner stops on for each spin.

Example 2: What Is Probability?
Probability is a measure of how likely it is that an event will happen. A probability is indicated by a number between 0 and 1. Some events are certain to happen, while others are impossible. In most cases, the probability of an event happening is somewhere between certain and impossible.
For example, consider a bag that contains only red cubes. If you were to select one cube from the bag, you are certain to pick a red one. We say that an event that is certain to happen has a probability of 1. If we were to reach into the same bag of cubes, it is impossible to select a yellow cube. An impossible event has a probability of 0.

The figure below shows the probability scale.

Answer:

Eureka Math Grade 7 Module 5 Lesson 1 Exercise Answer Key

Exercise 1.
Which color was the first to occur 10 times?
Answer:
Answers will vary, but green is the most likely.

Exercise 2.
Do you think it makes a difference who goes first to pick a color?
Answer:
Yes. The person who goes first could pick green.

Exercise 3.
Which color would you pick to give you the best chance of winning the game? Why would you pick that color?
Answer:
Green would give the best chance of winning the game because it has the largest section on the spinner.

Exercise 4.
Below are three different spinners. On which spinner is the green likely to win, unlikely to win, and equally likely to win?

Answer:
Green is likely to win on Spinner B, unlikely to win on Spinner C, and equally likely to win on Spinner A.

Exercise 5.
Decide where each event would be located on the scale above. Place the letter for each event in the appropriate place on the probability scale.
Event:
A. You will see a live dinosaur on the way home from school today.
B. A solid rock dropped in the water will sink.
C. A round disk with one side red and the other side yellow will land yellow side up when flipped.
D. A spinner with four equal parts numbered 1–4 will land on the 4 on the next spin.
E. Your full name will be drawn when a full name is selected randomly from a bag containing the full names of all of the students in your class.
F. A red cube will be drawn when a cube is selected from a bag that has five blue cubes and five red cubes.
G. Tomorrow the temperature outside will be -250 degrees.
Answer:
Answers are noted on the probability scale above.
Event:
A. Probability is 0, or impossible, as there are no live dinosaurs.
B. Probability is 1, or certain to occur, as rocks are typically more dense than the water they displace.
C. Probability is \(\frac{1}{2}\), as there are two sides that are equally likely to land up when the disk is flipped.

D. Probability of landing on the 4 would be \(\frac{1}{4}\), regardless of what spin was made. Based on the scale provided, this would indicate a probability halfway between impossible and equally likely, which can be classified as being unlikely to occur.

E. Probability is between impossible and equally likely to occur, assuming there are more than two students in the class. If there were two students, then the probability would be equally likely. If there were only one student in the class, then the probability would be certain to occur. If, however, there were more than two students, the probability would be between impossible and equally likely to occur.

F. Probability would be equally likely to occur as there are an equal number of blue and red cubes.
G. Probability is impossible, or 0, as there are no recorded temperatures at -250 degrees Fahrenheit or Celsius.

Exercise 6.
Design a spinner so that the probability of spinning a green is 1.
Answer:
The spinner is all green.

Exercise 7.
Design a spinner so that the probability of spinning a green is 0.
Answer:
The spinner can include any color but green.

Exercise 8.
Design a spinner with two outcomes in which it is equally likely to land on the red and green parts.
Answer:
The red and green areas should be equal.

An event that is impossible has a probability of 0 and will never occur, no matter how many observations you make. This means that in a long sequence of observations, it will occur 0% of the time. An event that is certain has a probability of 1 and will always occur. This means that in a long sequence of observations, it will occur 100% of the time.
Exercise 9.
What do you think it means for an event to have a probability of \(\frac{1}{2}\)?
Answer:
In a long sequence of observations, it would occur about half the time.

Exercise 10.
What do you think it means for an event to have a probability of \(\frac{1}{4}\)?
Answer:
In a long sequence of observations, it would occur about 25% of the time.

Eureka Math Grade 7 Module 5 Lesson 1 Problem Set Answer Key

Question 1.
Match each spinner below with the words impossible, unlikely, equally likely to occur or not occur, likely, and certain to describe the chance of the spinner landing on black.

Answer:

Question 2.
Decide if each of the following events is impossible, unlikely, equally likely to occur or not occur, likely, or certain to occur.
a. A vowel will be picked when a letter is randomly selected from the word lieu.
b. A vowel will be picked when a letter is randomly selected from the word math.
c. A blue cube will be drawn from a bag containing only five blue and five black cubes.
d. A red cube will be drawn from a bag of 100 red cubes.
e. A red cube will be drawn from a bag of 10 red and 90 blue cubes.
Answer:
a. Likely; most of the letters of the word lieu are vowels.
b. Unlikely; most of the letters of the word math are not vowels.
c. Equally likely to occur or not occur; the number of blue and black cubes in the bag is the same.
d. Certain; the only cubes in the bag are red.
e. Unlikely; most of the cubes in the bag are blue.

Question 3.
A shape will be randomly drawn from the box shown below. Decide where each event would be located on the probability scale. Then, place the letter for each event on the appropriate place on the probability scale.

Event:
A. A circle is drawn.
B. A square is drawn.
C. A star is drawn.
D. A shape that is not a square is drawn.
Probability Scale

Answer:

Question 4.
Color the squares below so that it would be equally likely to choose a blue or yellow square.

Answer:
Color five squares blue and five squares yellow.

Question 5.
Color the squares below so that it would be likely but not certain to choose a blue square from the bag.

Answer:
Color 6, 7, 8, or 9 squares blue and the rest any other color.

Question 6.
Color the squares below so that it would be unlikely but not impossible to choose a blue square from the bag.

Answer:
Color 1, 2, 3, or 4 squares blue and the others any other color.

Question 7.
Color the squares below so that it would be impossible to choose a blue square from the bag.

Answer:
Color all squares any color but blue.

Eureka Math Grade 7 Module 5 Lesson 1 Exit Ticket Answer Key

Question 1.
Decide where each of the following events would be located on the scale below. Place the letter for each event on the appropriate place on the probability scale.

The numbers from 1 to 10 are written on small pieces of paper and placed in a bag. A piece of paper will be drawn from the bag.
A. A piece of paper with a 5 is drawn from the bag.
B. A piece of paper with an even number is drawn.
C. A piece of paper with a 12 is drawn.
D. A piece of paper with a number other than 1 is drawn.
E. A piece of paper with a number divisible by 5 is drawn.
Answer:

The numbers from 1 to 10 are written on small pieces of paper and placed in a bag. A piece of paper will be drawn from the bag.
A. A piece of paper with a 5 is drawn from the bag.
B. A piece of paper with an even number is drawn.
C. A piece of paper with a 12 is drawn.
D. A piece of paper with a number other than 1 is drawn.
E. A piece of paper with a number divisible by 5 is drawn.

Engage NY Eureka Math 7th Grade Module 5 Lesson 3 Answer Key

Eureka Math Grade 7 Module 5 Lesson 3 Example Answer Key

Example 2: Equally Likely Outcomes
The sample space for the paper cup toss was on its side, right side up, and upside down.
The outcomes of an experiment are equally likely to occur when the probability of each outcome is equal.
Toss the paper cup 30 times, and record in a table the results of each toss.

Answer:

Eureka Math Grade 7 Module 5 Lesson 3 Exercise Answer Key

Exercises 1–6
Jamal, a seventh grader, wants to design a game that involves tossing paper cups. Jamal tosses a paper cup five times and records the outcome of each toss. An outcome is the result of a single trial of an experiment.
Here are the results of each toss:

Jamal noted that the paper cup could land in one of three ways: on its side, right side up, or upside down. The collection of these three outcomes is called the sample space of the experiment. The sample space of an experiment is the set of all possible outcomes of that experiment.
For example, the sample space when flipping a coin is heads, tails.
The sample space when drawing a colored cube from a bag that has 3 red, 2 blue, 1 yellow, and 4 green cubes is red, blue, yellow, green.

For each of the following chance experiments, list the sample space (i.e., all the possible outcomes).
Exercise 1.
Drawing a colored cube from a bag with 2 green, 1 red, 10 blue, and 3 black
Answer:
Green, red, blue, black

Exercise 2.
Tossing an empty soup can to see how it lands
Answer:
Right side up, upside down, on its side

Exercise 3.
Shooting a free throw in a basketball game
Answer:
Made shot, missed shot

Exercise 4.
Rolling a number cube with the numbers 1–6 on its faces
Answer:
1, 2, 3, 4, 5, or 6

Exercise 5.
Selecting a letter from the word probability
Answer:
p, r, o, b, a, i, I, t, y

Exercise 6.
Spinning the spinner:

Answer:
1, 2, 3, 4, 5, 6, 7, 8

Exercises 7–12
Exercise 7.
Using the results of your experiment, what is your estimate for the probability of a paper cup landing on its side?
Answer:
Answers will vary. The probability for the sample provided is \(\frac{19}{30}\).

Exercise 8.
Using the results of your experiment, what is your estimate for the probability of a paper cup landing upside down?
Answer:
Answers will vary. The probability for the sample provided is \(\frac{5}{30}\), or \(\frac{1}{6}\).

Exercise 9.
Using the results of your experiment, what is your estimate for the probability of a paper cup landing right side up?
Answer:
Answers will vary. The probability for the sample provided is \(\frac{6}{30}\), or \(\frac{1}{5}\).

Exercise 10.
Based on your results, do you think the three outcomes are equally likely to occur?
Answer:
Answers will vary, but, according to the sample provided, the outcomes are not equally likely.

Exercise 11.
Using the spinner below, answer the following questions.

a. Are the events spinning and landing on 1 or 2 equally likely?
b. Are the events spinning and landing on 2 or 3 equally likely?
c. How many times do you predict the spinner will land on each section after 100 spins?
Answer:
a. Yes. The areas of sections 1 and 2 are equal.
b. No. The areas of sections 2 and 3 are not equal.
c. Based on the areas of the sections, approximately 25 times each for sections 1 and 2 and 50 times for section 3.

Exercise 12.
Draw a spinner that has 3 sections that are equally likely to occur when the spinner is spun. How many times do you think the spinner will land on each section after 100 spins?
Answer:
The three sectors should be equal in area. Expect the spinner to land on each section approximately 33 times (30–35 times).

Eureka Math Grade 7 Module 5 Lesson 3 Problem Set Answer Key

Question 1.
For each of the following chance experiments, list the sample space (all the possible outcomes).
a. Rolling a 4-sided die with the numbers 1–4 on the faces of the die
b. Selecting a letter from the word mathematics
c. Selecting a marble from a bag containing 50 black marbles and 45 orange marbles
d. Selecting a number from the even numbers 2–14, including 2 and 14
e. Spinning the spinner below:

Answer:
a. 1, 2, 3, 4
b. m, a, t, h, e, i, c, s
c. Black, orange
d. 2, 4, 6, 8, 10, 12, 14
e. 1, 2, 3, 4

Question 2.
For each of the following, decide if the two outcomes listed are equally likely to occur. Give a reason for your answer.
a. Rolling a 1 or a 2 when a 6-sided number cube with the numbers 1–6 on the faces of the cube is rolled
b. Selecting the letter a or k from the word take
c. Selecting a black or an orange marble from a bag containing 50 black and 45 orange marbles
d. Selecting a 4 or an 8 from the even numbers 2–14, including 2 and 14
e. Landing on a 1 or a 3 when spinning the spinner below

Answer:
a. Yes. Each has the same chance of occurring.
b. Yes. Each has the same chance of occurring.
c. No. Black has a slightly greater chance of being chosen.
d. Yes. Each has the same chance of being chosen.
e. No. 1 has a larger area, so it has a greater chance of occurring.

Question 3.
Color the squares below so that it would be equally likely to choose a blue or yellow square.

Answer:
Answers will vary, but students should have the same number of squares colored blue as they have colored yellow.

Question 4.
Color the squares below so that it would be more likely to choose a blue than a yellow square.

Answer:
Answers will vary. Students should have more squares colored blue than yellow.

Question 5.
You are playing a game using the spinner below. The game requires that you spin the spinner twice. For example, one outcome could be yellow on the 1st spin and red on the 2nd spin. List the sample space (all the possible outcomes) for the two spins.

Answer:

Question 6.
List the sample space for the chance experiment of flipping a coin twice.
Answer:
There are four possibilities:

Eureka Math Grade 7 Module 5 Lesson 3 Exit Ticket Answer Key

The numbers 1–10 are written on note cards and placed in a bag. One card will be drawn from the bag at random.
Question 1.
List the sample space for this experiment.
Answer:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10

Question 2.
Are the events selecting an even number and selecting an odd number equally likely? Explain your answer.
Answer:
Yes. Each has the same chance of occurring. There are 5 even and 5 odd numbers in the bag.

Question 3.
Are the events selecting a number divisible by 3 and selecting a number divisible by 5 equally likely? Explain your answer.
Answer:
No. There are 3 numbers divisible by 3 (3, 6, and 9) but only 2 numbers divisible by 5 (5 and 10). So, the chance of selecting a number divisible by 3 is slightly greater than the chance of selecting a number divisible by 5.

Engage NY Eureka Math 7th Grade Module 5 Lesson 2 Answer Key

Eureka Math Grade 7 Module 5 Lesson 2 Example Answer Key

Example 2: Animal Crackers
A student brought a very large jar of animal crackers to share with students in class. Rather than count and sort all the different types of crackers, the student randomly chose 20 crackers and found the following counts for the different types of animal crackers. Estimate the probability of selecting a zebra.

Answer:
The estimated probability of picking a zebra is 3/20, or 0.15 or 15%. This means that an estimate of the proportion of the time a zebra will be selected is 0.15 or 15% of the time. This could be written as P(zebra) = 0.15, or the probability of selecting a zebra is 0.15.

Eureka Math Grade 7 Module 5 Lesson 2 Exercise Answer Key

Exercises 1–8: Carnival Game
At the school carnival, there is a game in which students spin a large spinner. The spinner has four equal sections numbered 1–4 as shown below. To play the game, a student spins the spinner twice and adds the two numbers that the spinner lands on. If the sum is greater than or equal to 5, the student wins a prize.

Play this game with your partner 15 times. Record the outcome of each spin in the table below.


Exercise 1.
Out of the 15 turns, how many times was the sum greater than or equal to 5?
Answer:
Answers will vary and should reflect the results from students playing the game 15 times. In the example above, eight outcomes had a sum greater than or equal to 5.

Exercise 2.
What sum occurred most often?
Answer:
5 occurred the most.

Exercise 3.
What sum occurred least often?
Answer:
6 and 8 occurred the least. (Anticipate a range of answers, as this was only done 15 times. We anticipate that 2 and 8 will not occur as often.)

Exercise 4.
If students were to play a lot of games, what fraction of the games would they win? Explain your answer.
Answer:
Based on the above outcomes, \(\frac{8}{15}\) represents the fraction of outcomes with a sum of 5 or more. To determine this, count how many games have a sum of 5 or more. There are 8 games out of the total 15 that have a sum of 5 or more.

Exercise 5.
Name a sum that would be impossible to get while playing the game.
Answer:
Answers will vary. One possibility is getting a sum of 100. Any sum less than 2 or greater than 8 would be correct.

Exercise 6.
What event is certain to occur while playing the game?
Answer:
Answers will vary. One possibility is getting a sum between 2 and 8 because all possible sums are between 2 and 8, inclusive.

When you were spinning the spinner and recording the outcomes, you were performing a chance experiment. You can use the results from a chance experiment to estimate the probability of an event. In Exercise 1, you spun the spinner 15 times and counted how many times the sum was greater than or equal to 5. An estimate for the probability of a sum greater than or equal to 5 is
P(sum ≥5) = \(\frac{\text { Number of observed occurrences of the event }}{\text { Total number of observations }}\)
Exercise 7.
Based on your experiment of playing the game, what is your estimate for the probability of getting a sum of 5 or more?
Answer:
Answers will vary. Students should answer this question based on their results. For the results indicated above, \(\frac{8}{15}\) or approximately 0.53 or 53% would estimate the probability of getting a sum of 5 or more.

Exercise 8.
Based on your experiment of playing the game, what is your estimate for the probability of getting a sum of exactly 5?
Answer:
Answers will vary. Students should answer this question based on their results. Using the above 15 outcomes, \(\frac{4}{15}\) or approximately 0.27 or 27% of the time represents an estimate for the probability of getting a sum of exactly 5.

Exercises 9–15
If a student randomly selected a cracker from a large jar:
Exercise 9.
What is your estimate for the probability of selecting a lion?
Answer:
\(\frac{2}{20}\) = \(\frac{1}{10}\) = 0.1

Exercise 10.
What is your estimate for the probability of selecting a monkey?
Answer:
\(\frac{4}{20}\) = \(\frac{1}{5}\) = 0.2

Exercise 11.
What is your estimate for the probability of selecting a penguin or a camel?
Answer:
\(\frac{(3+1)}{20}\) = \(\frac{4}{20}\) = \(\frac{1}{5}\) = 0.2

Exercise 12.
What is your estimate for the probability of selecting a rabbit?
Answer:
\(\frac{0}{20}\) = 0

Exercise 13.
Is there the same number of each kind of animal cracker in the jar? Explain your answer.
Answer:
No. There appears to be more elephants than other types of crackers.

Exercise 14.
If the student randomly selected another 20 animal crackers, would the same results occur? Why or why not?
Answer:
Probably not. Results may be similar, but it is very unlikely they would be exactly the same.

Exercise 15.
If there are 500 animal crackers in the jar, how many elephants are in the jar? Explain your answer.
Answer:
\(\frac{5}{20}\) = \(\frac{1}{4}\) = 0 .25; hence, an estimate for the number of elephants would be 125 because 25% of 500 is 125.

Eureka Math Grade 7 Module 5 Lesson 2 Problem Set Answer Key

Question 1.
Play a game using the two spinners below. Spin each spinner once, and then multiply the outcomes together. If the result is less than or equal to 8, you win the game. Play the game 15 times, and record your results in the table below. Then, answer the questions that follow.

a. What is your estimate for the probability of getting a product of 8 or less?
b. What is your estimate for the probability of getting a product of more than 8?
c. What is your estimate for the probability of getting a product of exactly 8?
d. What is the most likely product for this game?
e. If you play this game another 15 times, will you get the exact same results? Explain.
Answer:

a. Answers should be approximately 7, 8, or 9 divided by 15. The probability for the sample spins provided is \(\frac{9}{15}\), or \(\frac{3}{5}\).

b. Subtract the answer to part (a) from 1, or 1- the answer from part (a). Approximately 8, 7, or 6 divided by 15. The probability for the sample spins provided is \(\frac{6}{15}\), or \(\frac{2}{5}\).

c. Approximately 1 or 2 divided by 15. The probability for the sample spins provided is \(\frac{1}{15}\).

d. Possibilities are 4, 6, 8, and 12. The most likely product in the sample spins provided is 4.

e. No. Since this is a chance experiment, results could change for each time the game is played.

Question 2.
A seventh-grade student surveyed students at her school. She asked them to name their favorite pets. Below is a bar graph showing the results of the survey.

Use the results from the survey to answer the following questions.
a. How many students answered the survey question?
b. How many students said that a snake was their favorite pet?

Now, suppose a student is randomly selected and asked what his favorite pet is.
c. What is your estimate for the probability of that student saying that a dog is his favorite pet?
d. What is your estimate for the probability of that student saying that a gerbil is his favorite pet?
e. What is your estimate for the probability of that student saying that a frog is his favorite pet?
Answer:
a. 31
b. 5
c. (Allow any form.) \(\frac{9}{31}\), or approximately 0.29 or approximately 29%
d. (Allow any form.) \(\frac{2}{31}\), or approximately 0.06 or approximately 6%
e. \(\frac{0}{31}\), or 0 or 0%

Question 3.
A seventh-grade student surveyed 25 students at her school. She asked them how many hours a week they spend playing a sport or game outdoors. The results are listed in the table below.

a. Draw a dot plot of the results.

Suppose a student will be randomly selected.
b. What is your estimate for the probability of that student answering 3 hours?
c. What is your estimate for the probability of that student answering 8 hours?
d. What is your estimate for the probability of that student answering 6 or more hours?
e. What is your estimate for the probability of that student answering 3 or fewer hours?
f. If another 25 students were surveyed, do you think they would give the exact same results? Explain your answer.
g. If there are 200 students at the school, what is your estimate for the number of students who would say they play a sport or game outdoors 3 hours per week? Explain your answer.
Answer:
a.
b. \(\frac{7}{25}\) = 0.28 = 28%
c. \(\frac{1}{25}\) = 0.04 = 4%
d. \(\frac{3}{25}\) = 0.12 = 12%
e. \(\frac{19}{25}\) = 0.76 = 76%
f. No. Each group of 25 students could answer the question differently.

g. 200 ∙ (\(\frac{7}{25}\)) = 56
I would estimate that 56 students would say they play a sport or game outdoors 3 hours per week. This is based on estimating that, of the 200 students, \(\frac{7}{25}\) would play a sport or game outdoors 3 hours per week, as \(\frac{7}{25}\) represented the probability of playing a sport or game outdoors 3 hours per week from the seventh-grade class surveyed.

Question 4.
A student played a game using one of the spinners below. The table shows the results of 15 spins. Which spinner did the student use? Give a reason for your answer.

Answer:
Spinner B. Tallying the results: 1 occurred 6 times, 2 occurred 6 times, and 3 occurred 3 times. In Spinner B, the sections labeled 1 and 2 are equal and larger than section 3.

Eureka Math Grade 7 Module 5 Lesson 2 Exit Ticket Answer Key

In the following problems, round all of your decimal answers to three decimal places. Round all of your percents to the nearest tenth of a percent.
A student randomly selected crayons from a large bag of crayons. The table below shows the number of each color crayon in a bag. Now, suppose the student were to randomly select one crayon from the bag.

Question 1.
What is the estimate for the probability of selecting a blue crayon from the bag? Express your answer as a fraction, decimal, or percent.
Answer:
\(\frac{5}{30}\) = \(\frac{1}{6}\) ≈ 0.167 or 16.7%

Question 2.
What is the estimate for the probability of selecting a brown crayon from the bag?
Answer:
\(\frac{10}{30}\) = \(\frac{1}{3}\) ≈ 0.333 or 33.3%

Question 3.
What is the estimate for the probability of selecting a red crayon or a yellow crayon from the bag?
Answer:
\(\frac{9}{30}\) = \(\frac{3}{10}\) = 0.3 = 30%

Question 4.
What is the estimate for the probability of selecting a pink crayon from the bag?
Answer:
\(\frac{0}{30}\) = 0%

Question 5.
Which color is most likely to be selected?
Answer:
Brown

Question 6.
If there are 300 crayons in the bag, how many red crayons would you estimate are in the bag? Justify your answer.
Answer:
There are 6 out of 30, or \(\frac{1}{5}\) or 0.2, crayons that are red. Anticipate \(\frac{1}{5}\) of 300 crayons are red, or approximately 60 crayons.

Engage NY Eureka Math 7th Grade Module 5 End of Module Assessment Answer Key

Eureka Math Grade 7 Module 5 End of Module Assessment Task Answer Key

Round all decimal answers to the nearest hundredth.
Question 1.
You and a friend decide to conduct a survey at your school to see whether students are in favor of a new dress code policy. Your friend stands at the school entrance and asks the opinions of the first 100 students who come to campus on Monday. You obtain a list of all the students at the school and randomly select 60 to survey.
a. Your friend finds 34% of his sample in favor of the new dress code policy, but you find only 16%. Which do you believe is more likely to be representative of the school population? Explain your choice.
b. Suppose 25% of the students at the school are in favor of the new dress code policy. Below is a dot plot of the proportion of students who favor the new dress code for each of 100 different random samples of 50 students at the school.

If you were to select a random sample of 50 students and ask them if they favor the new dress code, do you think that your sample proportion will be within 0.05 of the population proportion? Explain.
c. Suppose ten people each take a simple random sample of 100 students from the school and calculate the proportion in the sample who favors the new dress code. On the dot plot axis below, place 10 values that you think are most believable for the proportions you could obtain.

Explain your reasoning.
Answer:
a. My students were randomly selected instead of only the early arrivers. My students would be more representative.

b. A little more than half of these 100 samples are between 0.20 and 0.30, so there is a good chance, but a value like 0.10 should be even better.

c. The values will still center around 0.25 but will tend to be much closer together than in part (b) where samples only had 50 students. This is because a larger sample size should show less variability.

Question 2.
Students in a random sample of 57 students were asked to measure their handspans (the distance from the outside of the thumb to the outside of the little finger when the hand is stretched out as far as possible). The graphs below show the results for the males and females.

a. Based on these data, do you think there is a difference between the population mean handspan for males and the population mean handspan for females? Justify your answer.
b. The same students were asked to measure their heights, with the results shown below.

Are these height data more or less convincing of a difference in the population mean height than the handspan data are of a difference in the population mean handspan? Explain.
Answer:
a. Yes. The handspans tend to be larger for males. All but two males are at least 20 cm. Less than “50%” of the female handspans are that large. The number of MADs by which they differ is significant: \(\frac{21.6-19.6}{1}\) = 2.

b. They are even more convincing because there is less overlap between the two distributions. The number of MADs by which they differ is significant: \(\frac{70.5-64.1}{1.7}\) = 3.76.

Question 3.
A student purchases a bag of “mini” chocolate chip cookies and, after opening the bag, finds one cookie that does not contain any chocolate chips! The student then wonders how unlikely it is to randomly find a cookie with no chocolate chips for this brand.
a. Based on the bag of 30 cookies, estimate the probability of this company producing a cookie with no
chocolate chips.
b. Suppose the cookie company claims that 90% of all the cookies it produces contain chocolate chips. Explain how you could simulate randomly selecting 30 cookies (one bag) from such a population to determine how many of the sampled cookies do not contain chocolate chips. Explain the details of your method so it could be carried out by another person.
c. Now, explain how you could use simulation to estimate the probability of obtaining a bag of 30 cookies with exactly one cookie with no chocolate chips.
d. If 90% of the cookies made by this company contain chocolate chips, then the actual probability of obtaining a bag of 30 cookies with one chipless cookie equals 0.143. Based on this result, would you advise this student to complain to the company about finding one cookie with no chocolate chips in her bag of 30? Explain.
Answer:
a. \(\frac{1}{30}\) ≈ 0.0333

b. Have a bag of 100 counting chips; 90 of them are red to represent cookies containing chips, and 10 of them are blue to represent cookies without chips. Pull out a chip, record its color, and put it back. Do this “30” times, and count how many are not red.

c. Repeat the above process from part (b) many, many times (e.g., 1,000). See what proportion of these 1,000 bags had exactly one blue chip. That number over 1,000 is your estimate of the probability of a bag of 30 cookies with one chocolate chip.

d. No. That is not that small of a probability. I would not find the value convincing that this did not just happen to her randomly.

Engage NY Eureka Math 7th Grade Module 5 Mid Module Assessment Answer Key

Eureka Math Grade 7 Module 5 Mid Module Assessment Task Answer Key

Round all decimal answers to the nearest hundredth.
Question 1.
Each student in a class of 38 students was asked to report how many siblings (brothers and sisters) he has. The data are summarized in the table below.

a. Based on the data, estimate the probability that a randomly selected student from this class is an only child.
b. Based on the data, estimate the probability that a randomly selected student from this class has three or more siblings.
c. Consider the following probability distribution for the number of siblings:

Explain how you could use simulation to estimate the probability that you will need to ask at least five students the question, “Are you an only child?” before you find one that is an only child.
Answer:
a. \(\frac{8}{38}\) ≈ 0.21
b. \(\frac{3+0+1+1}{38}\) = \(\frac{5}{38}\) ≈ 0.13

c. Put 100 counting chips in a bag with 15 red and 85 blue. Red represents the portion of students who don’t have a sibling, and blue represents the portion of students who have one or more siblings. Pull out chips until you get a red one (putting the chips back each time), and record the number of tries it took until a red chip was pulled out. Repeat 1000 times, and see how often you need to try 5 or more times to get a red chip.

Question 2.
A cell phone company wants to predict the probability of a seventh grader in your city, City A, owning a cell phone. Records from another city, City B, indicate that 201 of 1,000 seventh graders own a cell phone.
a. Assuming the probability of a seventh grader owning a cell phone is similar for the two cities, estimate the probability that a randomly selected seventh grader from City A owns a cell phone.
b. The company estimates the probability that a randomly selected seventh-grade male owns a cell phone is 0.25. Does this imply that the probability that a randomly selected seventh-grade female owns a cell phone is 0.75? Explain.
c. According to the data, which of the following is more likely?

• A seventh-grade male owning a cell phone
• A seventh grader owning a cell phone

Explain your choice.
Suppose the cell phone company sells three different plans to its customers:

• Pay-as-you-go: The customer is charged per minute for each call.
• Unlimited minutes: The customer pays a flat fee per month and can make unlimited calls with no additional charges.
• Basic plan: The customer is not charged per minute unless the customer exceeds 500 minutes in the month; then, the customer is charged per minute for the extra minutes.

Consider the chance experiment of selecting a customer at random and recording which plan she purchased.
d. What outcomes are in the sample space for this chance experiment?
e. The company wants to assign probabilities to these three plans. Explain what is wrong with each of the following probability assignments.
Case 1: The probability of pay-as-you-go is 0.40, the probability of unlimited minutes is 0.40, and the probability of the basic plan is 0.30.
Case 2: The probability of pay-as-you-go is 0.40, the probability of unlimited minutes is 0.70, and the probability of the basic plan is -0.10.

Now, consider the chance experiment of randomly selecting a cell phone customer and recording both the cell phone plan for that customer and whether or not the customer exceeded 500 minutes last month.
f. One possible outcome of this chance experiment is (pay-as-you-go, over 500). What are the other possible outcomes in this sample space?
g. Assuming the outcomes of this chance experiment are equally likely, what is the probability that the selected cell phone customer had a basic plan and did not exceed 500 minutes last month?
h. Suppose the company randomly selects 500 of its customers and finds that 140 of these customers purchased the basic plan and did not exceed 500 minutes. Would this cause you to question the claim that the outcomes of the chance experiment described in part (g) are equally likely? Explain why or why not.
Answer:
a. \(\frac{201}{1000}\) = 0.201

b. No. 0.75 would be the probability a male does not own a cell phone. The probabilities for females could be very different.

c. male = 0.25 > overall = 0.201 This implies the probability is a little higher for male seventh-grade students than for all seventh-grade students, so males are more likely to own a cell phone.

d. (1) pay-as-you-go
(2) unlimited minutes
(3) basic plan

e. Case 1: The sum of the three probabilities in the sample space is larger than 1, which cannot happen.
Case 2: There cannot be negative probabilities.

f. (pay-as-you-go, < 500)
(basic plan, ≥ 500)
(basic plan, < 500) (unlimited, > 500)
(unlimited, < 500)
(put exactly 500 in < 500)

g. \(\frac{1}{6}\) ≈ 0.167

h. \(\frac{140}{500}\) = 0.280
Yes. 0.280 is a lot higher than 0.167, which seems to indicate this outcome is more likely than some of the others.

Question 3.
In the game of darts, players throw darts at a circle divided into 20 wedges. In one variation of the game, the score for a throw is equal to the wedge number that the dart hits. So, if the dart hits anywhere in the 20 wedge, you earn 20 points for that throw.

a. If you are equally likely to land in any wedge, what is the probability you will score 20 points?
b. If you are equally likely to land in any wedge, what is the probability you will land in the upper right and score 20, 1, 18, 4, 13, or 6 points?
c. Below are the results of 100 throws for one player. Does this player appear to have a tendency to land in the upper right more often than we would expect if the player were equally likely to land in any wedge?

Answer:
a. \(\frac{1}{20}\) = 0.05
b. \(\frac{6}{20}\) = 0.30
c. \(\frac{7+6+3+4+6+4}{100}\) = \(\frac{30}{100}\) = 0.30
This is exactly how often we would predict this to happen.

Engage NY Eureka Math 7th Grade Module 6 End of Module Assessment Answer Key

Eureka Math Grade 7 Module 6 End of Module Assessment Task Answer Key

Question 1.
In the following two questions, lines AB and CD intersect at point O. When necessary, assume that seemingly straight lines are indeed straight lines. Determine the measures of the indicated angles.
a. Find the measure of ∠XOC.

b. Find the measures of ∠AOX, ∠YOD, and ∠DOB.

Answer:
a. x + 10 = 25 + 45
x + 10 – 10 = 70 – 10
x = 60
∠XOC = 60˚

b. 2x + 90 + x + (60 – x) = 180
2x + 150 – 150 = 180 – 150
2x = 30
\(\frac{1}{2}\) (2x) = \(\frac{1}{2}\)(30)
x = 15

∠AOX = 2(15)° = 30˚
∠YOD = 15˚
∠DOB = (60 – 15)° = 45˚

Question 2.
Is it possible to draw two different triangles that both have angle measurements of 40° and 50° and a side length of 5 cm? If it is possible, draw examples of these conditions, and label all vertices and angle and side measurements. If it is not possible, explain why.
Answer:
One possible solution:

Question 3.
In each of the following problems, two triangles are given. For each: (1) State if there are sufficient or insufficient conditions to show the triangles are identical, and (2) explain your reasoning.

Answer:
a. The triangles are identical by the three sides condition. △ABC ↔ △SRT
b. The triangles are identical by the two angles and included side condition. The marked side is between the given angles. △MNO ↔ △RQP

Question 4.
In the following diagram, the length of one side of the smaller shaded square is \(\frac{1}{3}\) the length of square ABCD. What percent of square ABCD is shaded? Provide all evidence of your calculations.

Answer:
Let x be the length of the side of the smaller shaded square. Then AD = 3x ; the length of the side of the larger shaded square is 3x – x = 2x.
Area_ABCD = (3x)² = 9x²
Area_{Large Shaded} = (2x)² = 4x²
Area_{Small Shaded} = (x)² = x²
Area_Shaded = 4x² + x² = 5x²
Percent Area_Shaded = \(\frac{1}{2}\)(100%) = 55 (\(\frac{5}{9}\)) %

Question 5.
Side \(\overline{E F}\) of square DEFG has a length of 2 cm and is also the radius of circle F. What is the area of the entire shaded region? Provide all evidence of your calculations.

Answer:
Area_{Circle F} = (π)(2 cm)² = 4π cm²
Area_{\(\frac{3}{4}\)Circle F} = \(\frac{3}{4}\) (4π cm²) = 3π cm²
Area_DEFG = (2 cm)(2 cm) = 4 cm²
Area_{Shaded Region} = 4 cm² + 3π cm²
Area_{Shaded Region} ≈ 13.4 cm²

Question 6.
For his latest design, a jeweler hollows out crystal cube beads (like the one in the diagram) through which the chain of a necklace is threaded. If the edge of the crystal cube is 10 mm, and the edge of the square cut is 6 mm, what is the volume of one bead? Provide all evidence of your calculations.

Answer:
VolumeLarge Cube = (10 mm)³ = 1,000 mm³
VolumeHollow = (10 mm)(6 mm)(6 mm) = 360 mm³
VolumeBead = 1,000 mm3 – 360 mm³ = 640 mm³

Question 7.
John and Joyce are sharing a piece of cake with the dimensions shown in the diagram. John is about to cut the cake at the mark indicated by the dotted lines. Joyce says this cut will make one of the pieces three times as big as the other. Is she right? Justify your response.

Answer:
VolumeTrapezoidal Prism = (\(\frac{1}{2}\)) (5 cm + 2.5 cm)(6 cm)(10 cm) = 225 cm³
VolumeTriangular Prism = (\(\frac{1}{2}\)) (2.5 cm)(6 cm)(10 cm) = 75 cm³
Joyce is right; the current cut would give 225 cm³ of cake for the trapezoidal prism piece and 75 cm³ of cake for the triangular prism piece, making the larger piece 3 times the size of the smaller piece (\(\frac{225}{75}\)) = 3).

Question 8.
A tank measures 4 ft. in length, 3 ft. in width, and 2 ft. in height. It is filled with water to a height of 1.5 ft. A typical brick measures a length of 9 in., a width of 4.5 in., and a height of 3 in. How many whole bricks can be added before the tank overflows? Provide all evidence of your calculations.
Answer:
Volume in tank not occupied by water:
V = (4 ft.)(3 ft.)(0.5 ft.) = 6 ft³
Volume_Brick = (9 in.)(4.5 in.)(3 in.) = 121.5 in³
Conversion (in³ to ft³): (121.5 in³ )(\(\frac{1 f t^{3}}{12^{3}-1 n^{3}}\)) = 0.0703125 ft³

Number of bricks that fit in the volume not occupied by water: (\(\frac{6 \mathrm{ft}^{3}}{0.07037 .25 \mathrm{ft}^{3}}\)) = 85 (\(\frac{1}{3}\))
Number of whole bricks that fit without causing overflow: 85

Question 9.
Three vertical slices perpendicular to the base of the right rectangular pyramid are to be made at the marked locations: (1) through \(\overline{A B}\), (2) through\(\overline{C D}\), and (3) through vertex E. Based on the relative locations of the slices on the pyramid, make a reasonable sketch of each slice. Include the appropriate notation to indicate measures of equal length.

Answer:
Sample response:

Question 10.
Five three-inch cubes and two triangular prisms have been glued together to form the composite three-dimensional figure shown in the diagram. Find the surface area of the figure, including the base. Provide all evidence of your calculations.

Answer:
19 square surfaces: 19(3 in.)² = 171 in²
4 triangular surfaces: (4) (\(\frac{1}{2}\)) (3 in.)(4 in.) = 24 in²
3 × 5 rectangular surface: (3 in.)(5 in.) = 15 in²
3 × 4 rectangular surface: (3 in.)(4 in.) = 12in²
6 × 5 rectangular surface: (6 in.)(5 in.) = 30 in²
6 × 4 rectangular surface: (6 in.)(4 in.) = 24 in²

Total surface area: 171 in² + 24 in² + 15 in² + 12 in² + 30 in² + 24 in² = 276 in²

Engage NY Eureka Math 7th Grade Module 6 Mid Module Assessment Answer Key

Eureka Math Grade 7 Module 6 Mid Module Assessment Task Answer Key

Question 1.
In each problem, set up and solve an equation for the unknown angles.
a. Four lines meet at a point. Find the measures m° and n°.

b. Two lines meet at the vertex of two rays. Find the measures m° and n°.

c. Two lines meet at a point that is the vertex of two rays. Find the measures m° and n°.

d. Three rays have a common vertex on a line. Find the measures m° and n°.

Answer:

a. n° = 90° , vertical angles

25° + (90°) + 40° + m° = 180°
155° + m° = 180°
155° – 155° + m° = 180° – 155°
m° = 25°

b. 50° + 90° + n° = 180°
140° + n° = 180°
140° – 140° + n° = 180° – 140°
n° = 40°

m° + 50° = 90°
m° + 50° – 50° = 90° – 50°
m° = 40°

c. m° + 52° = 90°
m° + 52° – 52° = 90° – 52°
m° = 38°

40 + 52 + (38) + n° = 180
130 + n° = 180
130 – 130 + n° = 180 – 130
n° = 50°

d. n° + 62° = 90°
n° + 62° – 62° = 90° – 62°
n° = 28°”

m° + 62° + (28°) + 27° = 180°
m° + 117° = 180
m° + 117° – 117° = 180° – 117°
m° = 63°

Question 2.
Use tools to construct a triangle based on the following given conditions.
a. If possible, use your tools to construct a triangle with angle measurements 20°, 55°, and 105°, and leave evidence of your construction. If it is not possible, explain why.
b. Is it possible to construct two different triangles that have the same angle measurements? If it is, construct examples that demonstrate this condition, and label all angle and length measurements. If it is not possible, explain why.
Answer:
a. Solutions will vary. An example of a correctly constructed triangle is shown here.

b. Solutions will vary; refer to the rubric.

Question 3.
In each of the following problems, two triangles are given. For each: (1) state if there are sufficient or insufficient conditions to show the triangles are identical, and (2) explain your reasoning.


Answer:

a. The triangles are identical by the two angles and included side condition. The marked side is between the given angles.
△ABC ↔ △YXZ

b. There is insufficient evidence to determine that the triangles are identical. In △DEF , the marked side is between the marked angles, but in △ABC , the marked side is not between the marked angles.

c. The triangles are identical by the two sides and included angle condition. △DEF ↔ △GIH

d. The triangles are not identical. In △ABC , the marked side is opposite ∠B . In △WXY , the marked side is opposite ∠W . ∠B and ∠W are not necessarily equal in measure.

Question 4.
Use tools to draw rectangle ABCD with AB = 2 cm and BC = 6 cm. Label all vertices and measurements.
Answer:

Question 5.
The measures of two complementary angles have a ratio of 3:7. Set up and solve an equation to determine the measurements of the two angles.
Answer:

3x + 7x = 90
10x = 90
(\(\frac{1}{10}\))10x = (\(\frac{1}{10}\))90
x = 9

Measure of Angle 1: 3(9) = 27 . The measure of the first angle is 27° .
Measure of Angle 2: 7(9) = 63 . The measure of the second angle is 63° .

Question 6.
The measure of the supplement of an angle is 12° less than the measure of the angle. Set up and solve an equation to determine the measurements of the angle and its supplement.
Answer:

Let y° be the number of degrees in the angle.

y + (y – 12) = 180
2y – 12 = 180
2y – 12 + 12 = 180 + 12
2y = 192
(\(\frac{1}{2}\))2y = (\(\frac{1}{2}\))192
y = 96

Measure of the angle: 96°
Measure of its supplement: (96)° – 12° = 84°

Question 7.
Three angles are at a point. The ratio of two of the angles is 2:3, and the remaining angle is 32° more than the larger of the first two angles. Set up and solve an equation to determine the measures of all three angles.
Answer:

2x + 3x + (3x + 32) = 360
8x + 32 = 360
8x + 32 – 32 = 360 – 32
8x = 328
(\(\frac{1}{8}\))8x = (\(\frac{1}{8}\))328
x = 41

Measure of Angle 1: 2(41)° = 82°
Measure of Angle 2: 3(41)° = 123°
Measure of Angle 3: 3(41)° + 32° = 155°

Question 8.
Draw a right triangle according to the following conditions, and label the provided information. If it is not possible to draw the triangle according to the conditions, explain why. Include a description of the kind of figure the current measurements allow. Provide a change to the conditions that makes the drawing feasible.
a. Construct a right triangle ABC so that AB = 3 cm, BC = 4 cm, and CA = 5 cm; the measure of angle B is 90°.
b. Construct triangle DEF so that DE = 4 cm, EF = 5 cm, and FD = 11 cm; the measure of angle D is 50°.
Answer:
a.

b. It is not possible to draw this triangle because the lengths of the two shorter sides do not sum to be greater than the longest side. In this situation, the total lengths of \(\overline{D E}\) and \(\overline{E F}\) are less than the length of \(\overline{F D}\); there is no way to arrange \(\overline{D E}\) and \(\overline{E F}\) so that they meet. If they do not meet, there is no arrangement of three non-collinear vertices of a triangle; therefore, a triangle cannot be formed. I would change \(\overline{E F}\)to 9 cm instead of 5 cm so that the three sides would form a triangle.

Engage NY Eureka Math 7th Grade Module 6 Lesson 27 Answer Key

Eureka Math Grade 7 Module 6 Lesson 27 Example Answer Key

Example 1.
A swimming pool holds 10,000 ft³ of water when filled. Jon and Anne want to fill the pool with a garden hose. The garden hose can fill a five – gallon bucket in 30 seconds. If each cubic foot is about 7.5 gallons, find the flow rate of the garden hose in gallons per minute and in cubic feet per minute. About how long will it take to fill the pool with a garden hose? If the hose is turned on Monday morning at 8:00 a.m., approximately when will the pool be filled?
Answer:
→ If the hose fills a 5 – gallon bucket in 30 seconds, how much would it fill in 1 minute? Find the flow rate in gallons per minute.
→ It would fill 10 gallons in 1 minute; therefore, the flow rate is 10 \(\frac{\mathrm{gal}}{\mathrm{min}}\).
→ Find the flow rate in cubic feet per minute.
Convert gallons to cubic feet: (10 gal.) \(\frac{1}{7.5} \frac{\mathrm{ft}^{3}}{\mathrm{gal}}\) = 1 \(\frac{1}{3}\)ft³
Therefore, the flow rate of the garden hose in cubic feet per minute is 1 \(\frac{1}{3} \frac{\mathrm{ft}^{3}}{\mathrm{~min}}\)

→ How many minutes would it take to fill the 10,000 ft³ pool?
\(\frac{10,000 \mathrm{ft}^{3}}{1 \frac{1}{3}\left(\frac{\mathrm{ft}^{3}}{1 \mathrm{~min}}\right)}\) = 7,500 min.
→ How many days and hours is 7,500 minutes?
(7,500 min.) \(\frac{1 \mathrm{~h}}{60 \mathrm{~min}}\) = 125 h, or 5 days and 5 hours

→ At what time will the pool be filled?
The pool begins to fill at 8:00 a.m. on Monday, so 5 days and 5 hours later on Saturday at 1:00 p.m., the pool will be filled.

Example 2.
A square pipe (a rectangular prism – shaped pipe) with inside dimensions of 2 in.×2 in. has water flowing through it at a flow speed of 3 \(\frac{\mathrm{ft}}{\mathrm{s}}\). The water flows into a pool in the shape of a right triangular prism, with a base in the shape of a right isosceles triangle and with legs that are each 5 feet in length. How long will it take for the water to reach a depth of
4 feet?
Answer:
→ This problem is slightly different than the previous example. In this example, we are given a flow speed (also known as linear flow speed) instead of a flow rate.

→ What do you think the term flow speed means based on what you know about flow rate and what you know about the units of each?
Flow speed in this problem is measured in feet per second. Flow rate in Example 1 is measured in gallons per minute (or cubic feet per minute).
Flow speed is the distance that the liquid moves in one unit of time.

→ Now, let’s go back to our example. The water is traveling at a flow speed of 3 \(\frac{\mathrm{ft}}{\mathrm{s}}\). This means that for each second that the water is flowing out of the pipe, the water travels a distance of 3 ft. Now, we need to determine the volume of water that passes per second; in other words, we need to find the flow rate.

→ Each second, the water in a cross – section of the pipe will travel 3 ft. This is the same as the volume of a right rectangular prism with dimensions 2 in.×2 in.×3 ft.

→ The volume of this prism in cubic feet is \(\frac{1}{6}\) ft.×\(\frac{1}{6}\) ft.×3 ft. = \(\frac{1}{12}\) ft³, and the volume of water flowing out of the pipe every second is \(\frac{1}{12}\) ft³. So, the flow rate is \(\frac{1}{12}\) \(\frac{\mathrm{ft}^{3}}{\mathrm{~s}}\).

→ Seconds is a very small unit of time when we think about filling up a pool. What is the flow rate in cubic feet per minute?
\(\frac{\frac{1}{12} \mathrm{ft}^{3}}{1 \mathrm{~s}} \cdot \frac{60 \mathrm{~s}}{1 \mathrm{~min}}\) = 5 \(\frac{\mathrm{ft}^{3}}{\min }\)

→ What is the volume of water that will be in the pool once the water reaches a depth of 4 ft.?
The volume of water in the pool will be \(\frac{1}{2}\)(5 ft.)(5 ft.)(4 ft.) = 50 ft³.

→ Now that we know our flow rate and the total volume of water in the pool, how long will it take for the pool to fill to a depth of 4 ft.?
\(\frac{50 \mathrm{ft}^{3}}{5 \frac{\mathrm{ft}^{3}}{\mathrm{~min}}}\) = 10 min.
It will take 10 minutes to fill the pool to a depth of 4 ft

Eureka Math Grade 7 Module 6 Lesson 27 Exercise Answer Key

Exercise 1.
A park fountain is about to be turned on in the spring after having been off all winter long. The fountain flows out of the top level and into the bottom level until both are full, at which point the water is just recycled from top to bottom through an internal pipe. The outer wall of the top level, a right square prism, is five feet in length; the thickness of the stone between outer and inner wall is 1 ft.; and the depth is 1 ft. The bottom level, also a right square prism, has an outer wall that is 11 ft. long with a 2 ft. thickness between the outer and inner wall and a depth of 2 ft. Water flows through a 3 in.×3 in. square pipe into the top level of the fountain at a flow speed of 4 \(\frac{\mathrm{ft}}{\mathrm{s}}\). Approximately how long will it take for both levels of the fountain to fill completely?

Answer:
Volume of top:
3 ft.×3 ft.×1 ft. = 9 ft³
Volume of bottom:
(7 ft.×7 ft.×2 ft.) – (5 ft.×5 ft.×2 ft.) = 48 ft³
Combined volume of both levels:
9 ft³ + 48 ft³ = 57 ft³

With a flow speed of 4 \(\frac{\mathrm{ft}}{\mathrm{s}}\) through a 3 in.×3 in. square pipe, the volume of water moving through the pipe in one second is equivalent to the volume of a right rectangular prism with dimensions 3 in.×3 in.×4 ft. The volume in feet is
\(\frac{1}{4}\) ft.×\(\frac{1}{4}\) ft.×4 ft. = \(\frac{1}{4}\) ft³. Therefore, the flow rate is \(\frac{1}{2}\) because \(\frac{1}{4}\) ft³ of water flows every second.

Volume of water that will flow in one minute:
\(\frac{\frac{1}{4} \mathrm{ft}^{3}}{1 \mathrm{~s}} \cdot \frac{60 \mathrm{~s}}{1 \mathrm{~min}}\) = 15 \(\frac{\mathrm{ft}^{3}}{\mathrm{~min}}\)
Time needed to fill both fountain levels: \(\frac{57 \mathrm{ft}^{3}}{15 \frac{\mathrm{ft}^{3}}{\min }}\) = 3.8 min.; it will take 3.8 minutes to fill both fountain levels.

Exercise 2.
A decorative bathroom faucet has a 3 in.×3 in. square pipe that flows into a basin in the shape of an isosceles trapezoid prism like the one shown in the diagram. If it takes one minute and twenty seconds to fill the basin completely, what is the approximate speed of water flowing from the faucet in feet per second?

Answer:
Volume of the basin in cubic inches:
\(\frac{1}{2}\) (3 in. + 15 in.)(10 in.)×4.5 in. = 405 in³
Approximate volume of the basin in cubic feet:
(405 in³ )(\(\frac{1 \mathrm{ft}^{3}}{1.728 \mathrm{in}^{3}}\)) = 0.234375 ft³
Based on the rate of water flowing out the faucet, the volume of water can also be calculated as follows:
Let s represent the distance that the water is traveling in 1 second.
3 in. ∙ 3 in. ∙ s = \(\frac{1}{4}\) ft. ∙ \(\frac{1}{4}\) ft. ∙ s ft. = 0.234375 ft³
Therefore, the speed of the water flowing from the faucet is 3.75 \(\frac{\mathrm{ft}}{\mathrm{s}}\).

Eureka Math Grade 7 Module 6 Lesson 27 Problem Set Answer Key

Question 1.
Harvey puts a container in the shape of a right rectangular prism under a spot in the roof that is leaking. Rainwater is dripping into the container at an average rate of 12 drops a minute. The container Harvey places under the leak has a length and width of 5 cm and a height of 10 cm. Assuming each raindrop is roughly 1 cm³, approximately how long does Harvey have before the container overflows?
Answer:
Volume of the container in cubic centimeters:
5 cm×5 cm×10 cm = 250 cm³
Number of minutes until the container is filled with rainwater:
(250 cm³)(\(\frac{1 \mathrm{~min}}{12 \mathrm{~cm}^{3}}\))≈20.8 min.

Question 2.
A large square pipe has inside dimensions 3 in.×3 in., and a small square pipe has inside dimensions 1 in.×1 in. Water travels through each of the pipes at the same constant flow speed. If the large pipe can fill a pool in 2 hours, how long will it take the small pipe to fill the same pool?
Answer:
If s is the length that the water travels in one minute, then in one minute the large pipe provides \(\frac{1}{4}\) ft. ∙ \(\frac{1}{4}\) ft. ∙ s ft. of water. In one minute, the small pipe provides one – ninth as much, \(\frac{1}{12}\) ft. ∙ \(\frac{1}{12}\) ft. ∙ s ft. of water. Therefore, it will take the small pipe nine times as long. It will take the small pipe 18 hours to fill the pool.

Question 3.
A pool contains 12,000 ft³ of water and needs to be drained. At 8:00 a.m., a pump is turned on that drains water at a flow rate of 10 ft³ per minute. Two hours later, at 10:00 a.m., a second pump is activated that drains water at a flow rate of 8 ft³ per minute. At what time will the pool be empty?
Answer:
Water drained in the first two hours: \(\frac{10 \mathrm{ft}^{3}}{1 \mathrm{~min}}\) ∙ 120 min. = 1,200 ft³
Volume of water that still needs to be drained: 12,000 ft³ – 1,200 ft³ = 10,800 ft³
Amount of time needed to drain remaining water with both pumps working:
10,800 ft³ (\(\frac{1 \mathrm{~min}}{10 \mathrm{ft}^{3}} + \frac{1 \mathrm{~min}}{8 \mathrm{ft}^{3}}\)) = 600 min., or 10 h.
The total time needed to drain the pool is 12 hours, so the pool will drain completely at 8:00 p.m.

Question 4.
In the previous problem, if water starts flowing into the pool at noon at a flow rate of 3 ft³ per minute, how much longer will it take to drain the pool?
Answer:
At noon, the first pump will have been on for four hours, and the second pump will have been on for two hours. The cubic feet of water drained by the two pumps together at noon is
240 min.(\(\frac{10 \mathrm{ft}^{3}}{1 \mathrm{~min}}\)) + 120 min.(\(\frac{8 \mathrm{ft}^{3}}{1 \mathrm{~min}}\)) = 3,360 ft³
Volume of water that still needs to be drained:
12,000 ft³ – 3,360 ft³ = 8,640 ft²
If water is entering the pool at 3 \(\frac{\mathrm{ft}^{3}}{\mathrm{~min}}\) but leaving it at 18 \(\frac{\mathrm{ft}^{3}}{\mathrm{~min}}\), the net effect is that water is leaving the pool at 15 \(\frac{\mathrm{ft}^{3}}{\mathrm{~min}}\)
8,640 ft³ (\(\frac{1 \mathrm{~min}}{15 \mathrm{ft}^{3}}\)) = 576 min., or 9 h. and 36 min.
The pool will finish draining at 9:36 p.m. the same day. It will take an additional 1 hour and 36 minutes to drain the pool.

Question 5.
A pool contains 6,000 ft³ of water. Pump A can drain the pool in 15 hours, Pump B can drain it in 12 hours, and Pump C can drain it in 10 hours. How long will it take all three pumps working together to drain the pool?
Answer:
Rate at which Pump A drains the pool: \(\frac{1}{15}\) pool per hour
Rate at which Pump B drains the pool: \(\frac{1}{12}\) pool per hour
Rate at which Pump C drains the pool: \(\frac{1}{10}\) pool per hour
Together, the pumps drain the pool at (\(\frac{1}{15}\) + \(\frac{1}{12}\) + \(\frac{1}{10}\)) pool per hour, or \(\frac{1}{4}\) pool per hour. Therefore, it will take
4 hours to drain the pool when all three pumps are working together.

Question 6.
A 2,000 – gallon fish aquarium can be filled by water flowing at a constant rate in 10 hours. When a decorative rock is placed in the aquarium, it can be filled in 9.5 hours. Find the volume of the rock in cubic feet (1 ft³ = 7.5 gal.)
Answer:
Rate of water flow into aquarium:
\(\frac{2,000 \text { gal }}{10 \mathrm{~h}} = \frac{200 \mathrm{gal}}{1 \mathrm{~h}}\)
Since it takes half an hour less time to fill the aquarium with the rock inside, the volume of the rock is
\(\frac{200 \text { gal }}{1 \mathrm{~h}}\) = 100 gal.
Volume of the rock:
100 gal.(\(\frac{1 \mathrm{ft}^{3}}{7.5 \mathrm{gal}}\))≈13.3 ft³; the volume of the rock is approximately 13.3 ft³.

Eureka Math Grade 7 Module 6 Lesson 27 Exit Ticket Answer Key

Question 1.
Jim wants to know how much his family spends on water for showers. Water costs $1.50 for 1,000 gallons. His family averages 4 showers per day. The average length of a shower is 10 minutes. He places a bucket in his shower and turns on the water. After one minute, the bucket has 2.5 gallons of water. About how much money does his family spend on water for showers in a 30 – day month?
Answer:
Number of gallons of water in one day of showering (four ten – minute showers): 4(10 min.)(\(\frac{2.5 \mathrm{gal}}{1 \mathrm{~min}}\)) = 100 gal.
Number of gallons of water in 30 days: (30 days)(\(\frac{100 \mathrm{gal}}{1 \mathrm{~min}}\)) = 3,000 gal.
Cost of showering for 30 days: (3,000 gal.)(\(\frac{\$ 1.50}{1,000 \mathrm{gal}}\)) = $4.50
The family spends $4.50 in a 30 – day month on water for showers.

Engage NY Eureka Math 7th Grade Module 6 Lesson 25 Answer Key

Eureka Math Grade 7 Module 6 Lesson 25 Example Answer Key

Example 1.
Calculate the volume of the following prism.

Answer:
→ What is the initial difficulty of determining the volume of this prism?
The base is not in the shape of a rectangle or triangle.

→ Do we have a way of finding the area of a kite in one step? If not, how can we find the area of a kite?
We do not have a way to find the area of a kite in one step. We can break the kite up into smaller shapes. One way would be to break it into two triangles, but it can also be broken into four triangles.

Once students understand that the base must be decomposed into triangles, allow them time to solve the problem.
→ Provide a numeric expression that determines the area of the kite – shaped base.
Area of the base: \(\frac{1}{2}\)(20 in.∙18 in.) + \(\frac{1}{2}\)(4 in.∙18 in.)

→ Find the volume of the prism.
Volume of the prism: (\(\frac{1}{2}\)(20 in.∙18 in.) + \(\frac{1}{2}\)(4 in.∙18 in.))(3 in.) = 648 in³

Example 2.
A container is shaped like a right pentagonal prism with an open top. When a cubic foot of water is dumped into the container, the depth of the water is 8 inches. Find the area of the pentagonal base.
Answer:
→ How can we use volume to solve this problem?
We know that the formula for the volume of a prism is V = Bh, where B represents the area of the pentagonal base and h is the height of the prism.

→ What information do we know from reading the problem?
The volume is 1 cubic foot, and the height of the water is 8 inches.

→ Knowing the volume formula, can we use this information to solve the problem?
We can use this information to solve the problem, but the information is given using two different dimensions.

→ How can we fix this problem?
We have to change inches into feet so that we have the same units.

→ How can we change inches into feet?
Because 12 inches make 1 foot, we have to divide the 8 inches by 12 to get the height in feet.

→ Convert 8 inches into feet.
\(\frac{8}{12}\) ft. = \(\frac{2}{3}\) ft.

→ Now that we know the volume of the water is 1 cubic foot and the height of the water is \(\frac{2}{3}\) feet, how can we determine the area of the pentagonal base?
Use the volume formula.
Use the information we know to find the area of the base.
1 ft³ = B(\(\frac{2}{3}\)ft.) Therefore, the area of the pentagonal base is \(\frac{3}{2}\) ft², or 1\(\frac{1}{2}\) ft².

Example 3.
Two containers are shaped like right triangular prisms, each with the same height. The base area of the larger container is 200% more than the base area of the smaller container. How many times must the smaller container be filled with water and poured into the larger container in order to fill the larger container?
Answer:
Solution by manipulating the equation of the volume of the smaller prism:
→ Let us call the area of the base of the smaller prism, B. Write an expression for the area of the larger base, and explain how it models the situation.
The base area of the larger prism is 3B because 200% more means that its area is 300% of B. Both prisms have the same height, h.

→ Compute the volume of the smaller prism.
The volume of the smaller prism is V_S = Bh.

→ What is the volume of the larger prism?
The volume of the larger prism is V_L = 3Bh.

→ How many times greater is the volume of the larger prism relative to the smaller prism?
\(\frac{3Bh}{Bh}\) = 3 The smaller container must be filled three times in order to fill the larger container.

Solution by substituting values for the smaller prism’s dimensions:
→ To solve this problem, create two right triangular prisms. What dimensions should we use for the smaller container?
Answers will vary, but for this example we will use a triangle that has a base of 10 inches and a height of 5 inches. The prism will have a height of 2 inches.

→ What is the area of the base for the smaller container? Explain.
The area of the base of the smaller container is 25 in² because A = \(\frac{1}{2}\)(10 in.)(5 in.) = 25 in².

→ What is the volume of the smaller container? Explain.
The volume of the smaller container is 50 in³ because V = 25 in² × 2 in. = 50 in³.

→ What do we know about the larger container?
The area of the larger container’s base is 200% more than the area of the smaller container’s base.
The height of the larger container is the same as the height of the smaller container.

→ If the area of the larger container’s base is 200% more than the area of the smaller container’s base, what is the area of the larger container’s base?
The area of the larger container’s base would be 25 in² + 2(25 in²) = 75 in².

→ What is the volume of the larger container? Explain.
The volume of the larger container is 150 in³ because V = 75 in² × 2 in. = 150 in³.

→ How many times must the smaller container be filled with water and poured into the larger container in order to fill the larger container? Explain.
The smaller container would have to be filled three times in order to fill the larger container. Each time you fill the smaller container, you will have 50 in³; therefore, you will need to fill the smaller container three times to get a volume of 150 in³.

→ Would your answer be different if we used different dimensions for the containers? Why or why not?
Our answer would not change if we used different dimensions. Because the area of the base of the larger container is triple the area of the base of the smaller container—and because the two heights are the same—the volume of the larger container is triple that of the smaller container.

Eureka Math Grade 7 Module 6 Lesson 25 Exercise Answer Key

Exercise 1.
a. Show that the following figures have equal volumes.

b. How can it be shown that the prisms will have equal volumes without completing the entire calculation?
Answer:
a. Volume of triangular prism:
\(\frac{1}{2}\)(8 cm × 9 cm) × 8 cm = 288 cm³

Volume of rectangular prism:
8 cm × 8 cm × 4.5 cm = 288 cm³

b. If one base can be cut up and rearranged to form the other base, then the bases have the same area. If the prisms have the same height, then the cutting and rearranging of the bases can show how to slice and rearrange one prism so that it looks like the other prism. Since slicing and rearranging does not change volume, the volumes are the same.

Exercise 2.
Two aquariums are shaped like right rectangular prisms. The ratio of the dimensions of the larger aquarium to the dimensions of the smaller aquarium is 3:2.
Addie says the larger aquarium holds 50% more water than the smaller aquarium.
Berry says that the larger aquarium holds 150% more water.
Cathy says that the larger aquarium holds over 200% more water.
Are any of the girls correct? Explain your reasoning.
Answer:
Cathy is correct. If the ratio of the dimensions of the larger aquarium to the dimensions of the smaller aquarium is 3:2, then the volume must be 1.5³, or 3.375 times greater than the smaller aquarium. Therefore, the larger aquarium’s capacity is 337.5% times as much water, which is 237.5% more than the smaller aquarium. Cathy said that the larger aquarium holds over 200% more water than the smaller aquarium, so she is correct.

Eureka Math Grade 7 Module 6 Lesson 25 Problem Set Answer Key

Question 1.
The pieces in Figure 1 are rearranged and put together to form Figure 2.

a. Use the information in Figure 1 to determine the volume of the prism.
b. Use the information in Figure 2 to determine the volume of the prism.
c. If we were not told that the pieces of Figure 1 were rearranged to create Figure 2, would it be possible to determine whether the volumes of the prisms were equal without completing the entire calculation for each?
Answer:
a. Volume: \(\frac{1}{2}\)(6.9 cm∙6 cm)(5 cm) = 103.5 cm³
b. Volume: (\(\frac{1}{2}\)(6.9 cm + 13.8 cm) ∙ 2 cm)(5 cm) = 103.5 cm³
c. Both prisms have the same height, so as long as it can be shown that both bases have the same area, both prisms must have equal volumes. We could calculate the area of the triangle base and the trapezoid base and find that they are equal in area and be sure that both volumes are equal.

Question 2.
Two right prism containers each hold 75 gallons of water. The height of the first container is 20 inches. The of the second container is 30 inches. If the area of the base in the first container is 6 ft², find the area of the base in the second container. Explain your reasoning.
Answer:
We know that the volume of each of the two containers is 75 gallons; therefore, the volumes must be equal.
In order to find the volume of the first container, we could multiply the area of the base (6 ft²) by the height
(20 inches). To find the volume of the second container, we would also multiply the area of its base, which we will call A (area in square feet), and the height (30 inches). These two expressions must equal each other since both containers have the same volume.
6 × 20 = A × 30
120 = 30A
120 ÷ 30 = 30A ÷ 30
4 = A
Therefore, the area of the base in the second container is 4 ft². Note: The units for the volume are 1 ft. × 1 ft. × 1 in. in this computation. Converting the inches to feet would make the computation in cubic feet, but it would not change the answer for A.

Question 3.
Two containers are shaped like right rectangular prisms. Each has the same height, but the base of the larger container is 50% more in each direction. If the smaller container holds 8 gallons when full, how many gallons does the larger container hold? Explain your reasoning.
Answer:
The larger container holds 18 gallons because each side length of the base is 1.5 times larger than the smaller container’s dimensions. Therefore, the area of the larger container’s base is 1.5², or 2.25 times larger than the smaller container. Because the height is the same in both containers, the volume of the larger container must be 2.25 times larger than the smaller container. 8 gal. × 2.25 = 18 gal.

Question 4.
A right prism container with the base area of 4 ft² and height of 5 ft. is filled with water until it is 3 ft. deep. If a solid cube with edge length 1 ft. is dropped to the bottom of the container, how much will the water rise?
Answer:
The volume of the cube is 1 ft³. Let the number of feet the water will rise be x. Then, the volume of the water over the 3 ft. mark is 4 x ft³ because this represents the area of the base (4 ft²) times the height (x). Because the volume of the cube is 1 ft³, 4 x ft³ must equal 1 ft³.
4x = 1
4x ÷ 4 = 1 ÷ 4
x = \(\frac{1}{4}\)
Therefore, the water will rise \(\frac{1}{4}\) ft., or 3 inches.

Question 5.
A right prism container with a base area of 10 ft² and height 9 ft. is filled with water until it is 6 ft. deep. A large boulder is dropped to the bottom of the container, and the water rises to the top, completely submerging the boulder without causing overflow. Find the volume of the boulder.
Answer:
The increase in volume is the same as the volume of the boulder. The height of the water increases 3 ft. Therefore, the increase in volume is 10 ft² (area of the base) multiplied by 3 ft. (i.e., the change in height).
V = 10 ft² × 3 ft. = 30 ft³
Because the increase in volume is 30 ft³, the volume of the boulder is 30 ft³.

Question 6.
A right prism container with a base area of 8 ft² and height 6 ft. is filled with water until it is 5 ft. deep. A solid cube is dropped to the bottom of the container, and the water rises to the top. Find the length of the cube.
Answer:
When the cube is dropped into the container, the water rises 1 foot, which means the volume increases 8 cubic feet. Therefore, the volume of the cube must be 8 cubic feet. We know that the length, width, and height of a cube are equal, so the length of the cube is 2 feet because 2 ft. × 2 ft. × 2 ft. = 8 ft³, which is the volume of the cube.

Question 7.
A rectangular swimming pool is 30 feet wide and 50 feet long. The pool is 3 feet deep at one end, and 10 feet deep at the other.
a. Sketch the swimming pool as a right prism.
b. What kind of right prism is the swimming pool?
c. What is the volume of the swimming pool in cubic feet?
d. How many gallons will the swimming pool hold if each cubic feet of water is about 7.5 gallons?
Answer:
a.

b. The swimming pool is a right trapezoidal prism.

c. Area of base = \(\frac{50 \mathrm{ft} \cdot(10 \mathrm{ft} + 3 \mathrm{ft})}{2}\) = 325 ft²
Volume of pool = 325 ft² × 30 ft. = 9,750 ft³

d. (9,750 ft³ ) \(\frac{(7.5 \mathrm{gal})}{1 \mathrm{ft}^{3}}\) = 73,125 gal. The pool will hold 73,125 gal.

Question 8.
A milliliter (mL) has a volume of 1 cm³. A 250 mL measuring cup is filled to 200 mL. A small stone is placed in the measuring cup. The stone is completely submerged, and the water level rises to 250 mL.
a. What is the volume of the stone in cm³?
b. Describe a right rectangular prism that has the same volume as the stone.
Answer:
a. When the stone is dropped into the measuring cup, the increase in volume is 250 mL – 200 mL = 50 mL. We know that 1 mL has a volume of 1 cm³; therefore, the stone has a volume of 50 cm³.

b. Answers will vary. Possible answers are listed below.
1 cm × 1 cm × 50 cm
1 cm × 2 cm × 25 cm
1 cm × 5 cm × 10 cm
2 cm × 5 cm × 5 cm

Eureka Math Grade 7 Module 6 Lesson 25 Exit Ticket Answer Key

Question 1.
Determine the volume of the following prism. Explain how you found the volume.

Answer:
To find the volume of the prism, the base must be decomposed into triangles and rectangles since there is no way to find the area of the base as is. The base can be decomposed into two triangles and a rectangle, and their areas must be summed to find the area of the base. Once the area of the base is determined, it should be multiplied by the height to find the volume of the entire prism.
Area of both triangles: 2(\(\frac{1}{2}\)(5 in. × 6 in.)) = 30 in²
Area of the rectangle: 15 in. × 5 in. = 75 in²
Total area of the base: (30 + 75) in² = 105 in²
Volume of the prism: (105 in²)(1.5 in.) = 157.5 in³