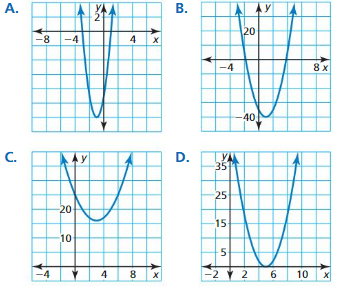
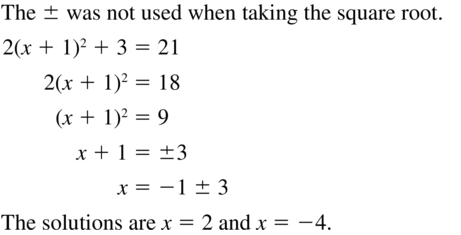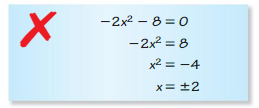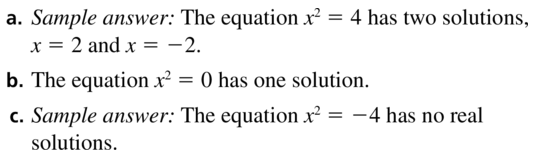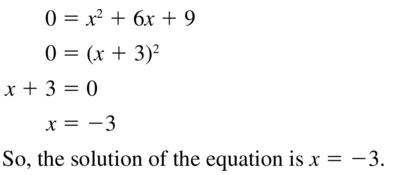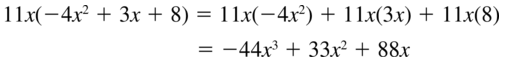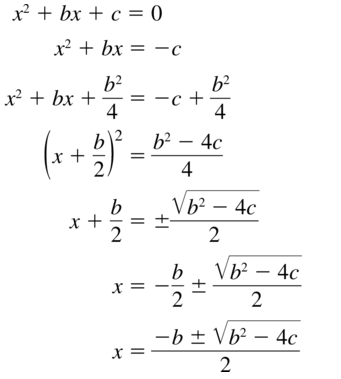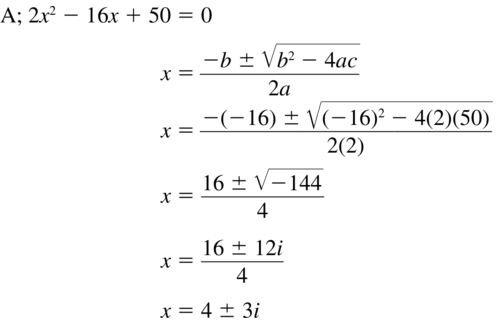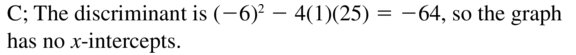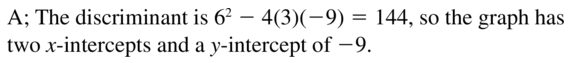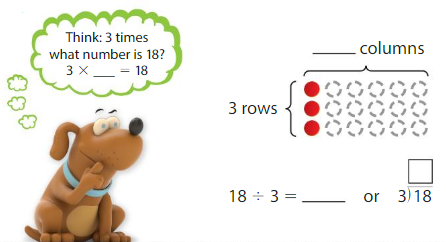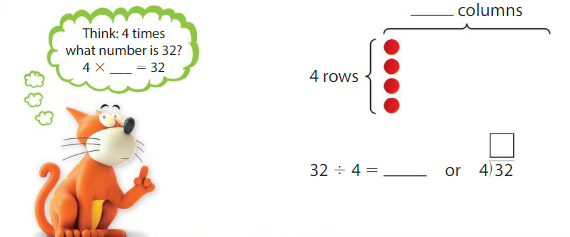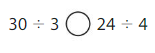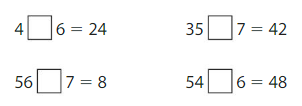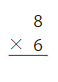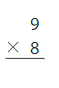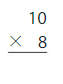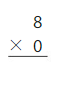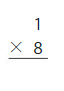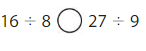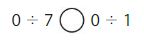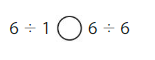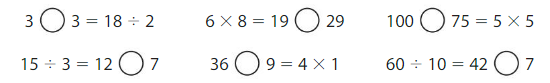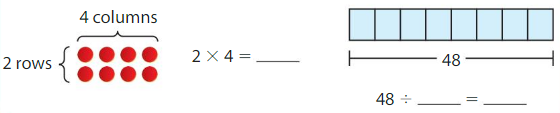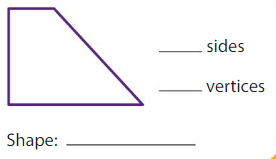Big Ideas Math Grade 3 Chapter 4 Division Facts and Strategies Solutions in the pdf format is provided here. Students have to be perfect in the basics of mathematics. So, everyone must download free Big ideas Math Book Grade 3 Chapter 4 Division Facts and Strategies Answer Key PDFand start their preparation. This handy and user-friendly answer key provides the answer and detailed solution for each and every problem in BIM 3rd Grade 4th Chapter Textbook. It will help the students while doing assignments and homework.
Big Ideas Math 3rd Grade Chapter 4 Division Facts and Strategies Answer Key
By solving the questions from Big Ideas Math Book Grade 3 Chapter 4 Division Facts and Strategies, you will know how to divide two numbers and different methods to solve it. The different topics covered in the Division Facts and Strategies chapter are Use Arrays to Divide, Relate Multiplication and Division, Divide by 2, 5, or 10, Divide by 3 or 4, Divide by 6 or 7, Divide by 8 or 9, and Divide by 0 or 1.
After solving the division problems from all these lessons, you have practice strategies where you can check your skills. The success criteria of Big Ideas Math Answers Grade 3 Chapter 4 Divison Facts and Strategies is able to compare multiplication and divison, know what is dividend, divisor, and quotient and can explain divison equation in an array. For the perfect preparation, you can tap on the links and download Answers for Big Ideas Math Book Grade 3 Chapter 4 Division Facts and Strategies.
Lesson – 1: Use Arrays to Divide
Lesson – 2: Relate Multiplication and Division
Lesson – 3: Divide by 2, 5, or 10
Lesson – 4: Divide by 3 or 4
Lesson – 5: Divide by 6 or 7
Lesson – 6: Divide by 8 or 9
Lesson – 7: Divide by 0 or 1
Lesson – 8: Practice Division Strategies
Lesson – 9: Problem Solving: Division
Performance Task
Lesson 4.1 Use Arrays to Divide
Explore and Grow
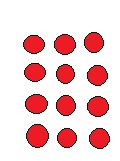
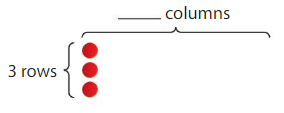
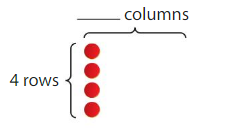
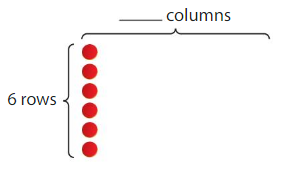
Build an array to model 12. Draw the array.
Number of rows: _______
Number in each row: ______
Answer:
Number of rows: 4
Number in each row: 3
Structure
Compare your array with your partner’s array. How are they the same? How are they different?
Answer: The number of counters is the same but the rows and columns are different.
Think and Grow: Division and Arrays
Example
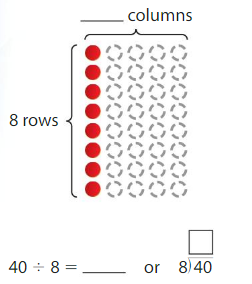
There are 40 counters. The counters are in5 equal rows. How many counters are in each row?
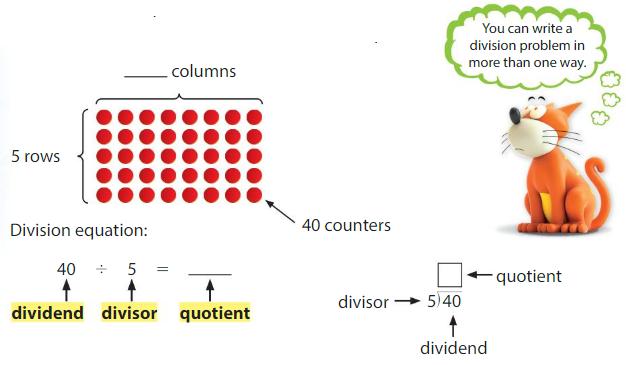
There are ______ counters in each row.
Answer: 8
Explanation:
Number of rows = 5
Total number of counters = 40
So, the division equation is 40 ÷ 5 = 8
There are 8 counters in each row.
Show and Grow
Find the quotient.
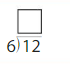
Question 1.

14 ÷ 2 = _____
Answer: 7
Explanation:
Number of counters = 14
Number of rows = 2
To find the quotient you have to divide the number of counters by the number of rows.
14 ÷ 2 = 7
Thus the number of columns in each row = 7
Question 2.

12 ÷ 3 = ______
Answer: 4
Explanation:
Number of counters = 12
Number of rows = 3
To find the quotient you have to divide the number of counters by the number of rows.
12 ÷ 3 = 4
Thus the number of columns in each row = 4
Question 3.
There are 20 counters. The counters are in 4 equal rows. How many counters are in each row?
4 rows of _____
20 ÷ 4 = _____
Answer: 5
Explanation:
Given,
There are 20 counters. The counters are in 4 equal rows.
To find the quotient you have to divide the number of counters by the number of rows.
20 ÷ 4 = 5
4 rows of 5
There are 5 counters in each row.
Question 4.
You have 21 counters. You arrange them with 7 counters in each row. How many rows of counters do you make?
____ rows of 7
21 ÷ 7 = _____
Answer: 3
Explanation:
Given,
You have 21 counters. You arrange them with 7 counters in each row.
21 ÷ 7 = 3
3 rows 7
Thus you make 3 rows of 7 counters.
Apply and Grow: Practice
Question 5.
There are 25 counters. The counters are in 5 equal rows. How many counters are in each row?
5 rows of _____
25 ÷ 5 = _____
Answer: 5
Explanation:
Given,
There are 25 counters.
The counters are in 5 equal rows.
To find the quotient you have to divide the number of counters by the number of rows.
25 ÷ 5 = 5
There are 5 counters in each row.
Question 6.
There are 48 counters. The counters are in 8 equal rows. How many counters are in each row?
8 rows of _____
48 ÷ 8 = _____
Answer: 6
Explanation:
Given,
There are 48 counters. The counters are in 8 equal rows.
To find the quotient you have to divide the number of counters by the number of rows.
48 ÷ 8 = 6
8 rows of 6 counters
There are 6 counters in each row.
Question 7.
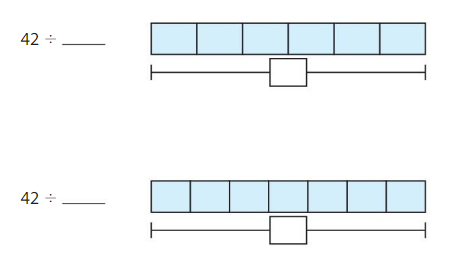
You have 42 counters. You arrange them with 6 counters in each row. How many rows of counters do you make?
____ rows of 6
42 ÷ 6 = _____
Answer: 7
Explanation:
Given,
You have 42 counters. You arrange them with 6 counters in each row.
7 rows of 6
42 ÷ 6 = 7
There are 7 rows of counters.
Question 8.
You have 27 counters. You arrange them with 9 counters in each row. How many rows of counters do you make?
____ rows of 9
27 ÷ 9 = _____
Answer: 3
Explanation:
Given that,
You have 27 counters. You arrange them with 9 counters in each row.
27 ÷ 9 = 3
3 rows of 9.
There are 3 rows of counters.
Write a division equation for the array.
Question 9.

_____ ÷ _____ = _____
Answer: 4 ÷ 2 = 2
Explanation:
There are 4 rows and 2 counters.
The division equation for the array is 4 ÷ 2 = 2
Question 10.

____ ÷ _____ = _____
Answer: 40 ÷ 4 = 10
Explanation:
There are 4 rows and 40 counters.
The division equation for the array is 40 ÷ 4 = 10
Question 11.
YOU BE THE TEACHER
Your friend has 63 counters in 7 equal rows. Your friend says that finding 7 ÷ 63 will give the number of columns. Is your friend correct? Explain.
Answer: No your friend is incorrect.
Explanation:
Given,
Your friend has 63 counters in 7 equal rows.
Your friend says that finding 7 ÷ 63 will give the number of columns.
Your friend is incorrect because you have to divide the number of counters by a number of equal rows.
63 ÷ 7 = 9
There are 9 columns.
Think and Grow: Modeling Real Life
Two groups of students are playing a flip and find game. Your group arranges 48 cards in 8 equal rows. The other group arranges 28 cards in 4 equal rows. Which group has rows with more cards?
Draw:
Division equations:
_______ has rows with more cards.
Explanation:
Given,
Two groups of students are playing a flip and find game.
Your group arranges 48 cards in 8 equal rows.
48 ÷ 8 = 6 in each row
The other group arranges 28 cards in 4 equal rows.
28 ÷ 4 = 7 in each row.
The second group has 7 rows with more cards.
Show and Grow
Question 12.
Newton arranges 12 magnets in 6 equal rows. Descartes arranges 15 magnets in 3 equal rows. Who has rows with more magnets?

Answer:
Given,
Newton arranges 12 magnets in 6 equal rows.
12 ÷ 6 = 2
Descartes arranges 15 magnets in 3 equal rows.
15 ÷ 3 = 5
Thus Descartes has 5 rows with more magnets.
Question 13.
You have 18 jars of green slime and 12 jars of purple slime at a party. Each guest takes 3 jars. There are none left. How many guests are at the party?

Answer:
Given that,
You have 18 jars of green slime and 12 jars of purple slime at a party.
18 + 12 = 30 jars
Each guest takes 3 jars. There are none left.
30 ÷ 3 = 10
Thus there are 10 guests at the party.
Use Arrays to Divide Homework & Practice 4.1
Find the quotient.
Question 1.

10 ÷ 2 = _____
Answer: 5
Explanation:
Number of counters = 10
Number of rows = 2
To find the quotient you have to divide the number of counters by the number of rows.
10 ÷ 2 = 5
Thus there are 5 counters in each row.
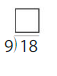
Question 2.

35 ÷ 5 = _____
Answer: 7
Explanation:
Number of counters = 35
Number of rows = 5
To find the quotient you have to divide the number of counters by the number of rows.
35 ÷ 5 = 7
Thus there are 7 counters in each row.
Question 3.
There are 9 counters. The counters are in 3 equal rows. How many counters are in each row?
3 rows of ____
9 ÷ 3 = ____
Answer: 3
Explanation:
Given that,
There are 9 counters. The counters are in 3 equal rows.
To find the quotient you have to divide the number of counters by the number of rows.
9 ÷ 3 = 3
3 rows of 3
Thus there are 3 counters in each row.
Question 4.
There are 60 counters. The counters are in 6 equal rows. How many counters are in each row?
6 rows of _____
60 ÷ 6 = ____
Answer: 10.
Explanation:
Given,
There are 60 counters.
The counters are in 6 equal rows.
To find the number of counters in each row you have to divide the total number of counters by the number of rows.
60 ÷ 6 = 10
6 rows of 10 counters
Thus there are 10 counters in each row.
Question 5.
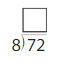
You have 72 counters. You arrange them with 8 counters in each row. How many rows of counters do you make?
____ rows of 8
72 ÷ 8 = ____
Answer: 9
Explanation:
Given,
You have 72 counters. You arrange them with 8 counters in each row.
To find the number of counters in each row you have to divide the total number of counters by the number of rows.
72 ÷ 8 = 9
9 rows of 8.
Thus there are 9 counters in each row.
Question 6.
You have 24 counters. You arrange them with 6 counters in each row. How many rows of counters do you make?
____ rows of 6
24 ÷ 6 = ____
Answer: 4
Explanation:
Given,
You have 24 counters. You arrange them with 6 counters in each row.
24 ÷ 6 = 4
4 rows of 6
Thus there are 4 counters in each row.
Question 7.
Writing
How can you use an array to find 35 ÷ 7?
Answer: 5
Explanation:
Number of counters = 35
Number of rows = 7
To find the number of counters in each row you have to divide the total number of counters by the number of rows.
35 ÷ 7 = 5
Question 8.
Precision
Label the parts of the division problem using quotient, dividend and divisor.
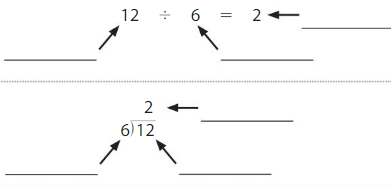
Answer:
12 is dividend
6 is divisor and
2 is quotient
Question 9.
Modeling Real Life
Your apartment building has 40 mailboxes in 5 equal rows. Your friend’s apartment building has 40 mailboxes in 4 equal rows. Which apartment building has rows with more mailboxes?
Answer: Your friend’s apartment building 10 rows with more mailboxes
Explanation:
Given,
Your apartment building has 40 mailboxes in 5 equal rows.
40 ÷ 5 = 8
Your friend’s apartment building has 40 mailboxes in 4 equal rows.
40 ÷ 4 = 10
Thus Your friend’s apartment building 10 rows with more mailboxes.
Question 10.
Modeling Real Life
There are 8 snack bags of pretzels and 10 snack bags of popcorn. The bags are divided equally between 9 friends. How many snack bags does each friend get?

Answer:
Given,
There are 8 snack bags of pretzels and 10 snack bags of popcorn.
8 + 10 = 18 snack bags
The bags are divided equally between 9 friends.
18 ÷ 9 = 2
Thus each friend gets 2 snack bags.
Review & Refresh
Find the missing factor
Question 11.
____ × 2 = 20
Answer: 10
Explanation:
Let the missing factor be a.
a × 2 = 20
a = 20/2
a = 10
Thus the missing factor is 10.
Question 12.
1 × ____ = 5
Answer: 5
Explanation:
Let the missing factor be b.
1 × b = 5
b = 5/1
b = 5
Thus the missing factor is 5.
Question 13.
____ × 6 = 0
Answer: 0
Explanation:
Let the missing factor be c.
c × 6 = 0
c = 0/6
c = 0
Thus the missing factor is 0.
Question 14.
1 × ___ = 0
Answer: 0
Explanation:
Let the missing factor be d.
1 × d = 0
d = 0/1
d = 0
Thus the missing factor is 0.
Question 15.
____ × 4 = 40
Answer: 10
Explanation:
Let the missing factor be e.
e × 4 = 40
e = 40/4
e = 10
Thus the missing factor is 10.
Question 16.
7 × ____ = 7
Answer: 1
Explanation:
Let the missing factor be f.
7 × f = 7
f = 7/7
f = 1
Thus the missing factor is 1.
Lesson 4.2 Relate Multiplication and Division
Explore and Grow
Use 24 counters to make an array. Draw the array. Write a multiplication equation and a division equation for the array.
____ × ____ = _____
_____ ÷ ____ = ____
Answer: 6 × 4 = 24
24 ÷ 6 = 4
Explanation:

The division equation is 24 ÷ 6 = 4 or 24 ÷ 4 = 6
Structure
Compare your equations to your partner’s equations. How are they the same? How are they different?
Answer:
Both the equations are the same but the rows and columns are different.
Think and Grow: Multiplication and Division
A fact family is a group of related facts that uses the same numbers.

Answer:
Multiplication:
5 rows of 6 counters
5 × 6 = 30
30 counters
Division:
30 counters in 5 equal rows
30 ÷ 5 = 6
60 counters in each row.
Fact family for 5, 6 and 30:
5 × 6 = 30
6 × 5 = 30
30 ÷ 5 = 6
30 ÷ 6 = 5
Show and Grow
Use the array to complete the equations.
Question 1.

3 × ____ = 24
24 ÷ 3 = ____
Answer: 8
Explanation:
Number of rows = 3
Number of counters = 24
To find the number of counters in each row you have to divide the total number of counters by the number of rows.
24 ÷ 3 = 8
3 × x = 24
x = 24/3
x = 8
Question 2.

4 × ____ = 20
20 ÷ 4 = _____
Answer: 5
Explanation:
Number of rows = 4
Number of counters = 20
To find the number of counters in each row you have to divide the total number of counters by the number of rows.
4 × x = 20
x = 20/4
x = 5
20 ÷ 4 = 5
Question 3.
Draw an array to find 2 × 7. Write the other facts in the fact family.
2 × 7 = _____
___________
___________
___________
Answer: 14
Explanation:
The fact family for the numbers 2, 7 and 14
2 × 7 = 14
7 × 2 = 14
14 ÷ 2 = 7
14 ÷ 7 = 2
Apply and Grow: Practice
Question 4.
Draw an array to find 3 × 6.
Write the other 3 facts in the fact family.
3 × 6 = ______
____________
_____________
____________
Answer: 18
Explanation:

The fact family for 3, 6 and 18 are
3 × 6 = 18
6 × 3 = 18
18 ÷ 3 = 6
18 ÷ 6 = 3
Complete the fact family.
Question 5.
7 × ____ = 70
____ × 7 = 70
70 ÷ 10 = ____
70 ÷ ___ = 10
Answer:
The fact family for 7, 10 and 70 are:
7 × 10 = 70
10 × 7 = 70
70 ÷ 10 = 7
70 ÷ 7 = 10
Question 6.
5 × ____ = 40
____ × 5 = 40
40 ÷ 8 = _____
40 ÷ ____ = 8
Answer:
The fact family for 5, 8 and 40 are:
5 × 8 = 40
8 × 5 = 40
40 ÷ 8 = 5
40 ÷ 5 = 8
Write the fact family for the numbers.
Question 7.
2, 5, 10
Answer:
The fact family for 2, 5 and 10 are:
2 × 5 = 10
5 × 2 = 10
10 ÷ 2 = 5
10 ÷ 5 = 2
Question 8.
4, 3, 12
Answer:
The fact family for 3, 4 and 12 are:
4 × 3 = 12
3 × 4 = 12
12 ÷ 3 = 4
12 ÷ 4 = 3
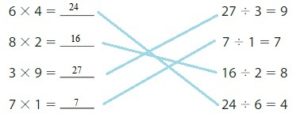
Question 9.
Structure
Find each product. Then match the multiplication fact with the related division fact.
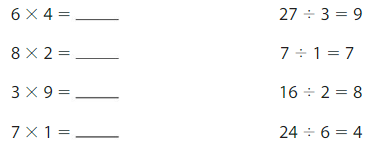
Answer:
Question 10.
DIG DEEPER!
Is 4 × 6 = 24 part of the fact family for 3 × 8 = 24? Explain.
Answer: No. Because the rows and columns are different.
Think and Grow: Modeling Real Life
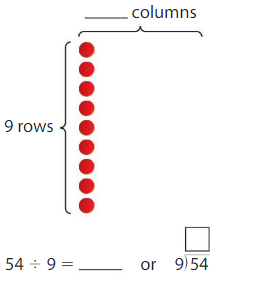
Your teacher divides the items shown equally among 9 students. Write two equations that you can use to show how many straws each student gets.
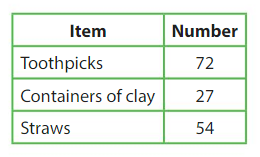
Division equation:
Multiplication equation:
Answer:
Your teacher divides the items shown equally among 9 students.
Straws – 54
54 ÷ 9 = 6
Thus each student gets 6 straws.
Division Equation is 54 ÷ 9 = 6
Multiplication equation 9 × 6 = 54
Show and Grow
Question 11.
Use the table above to write two equations that you can use to show how many containers of clay each student gets.
Answer:
Your teacher divides the items shown equally among 9 students.
Containers of the day – 27
27 ÷ 9 = 3
Division Equation is 27 ÷ 9 = 3
Multiplication equation is 3 × 9 = 27
Question 12.
Use the table above to find how many more toothpicks students will get than straws.

Answer:
Your teacher divides the items shown equally among 9 students.
Toothpicks – 72
72 ÷ 9 = 8
Each student gets 8 toothpicks
Straws – 54
54 ÷ 9 = 6
Thus each student gets 6 straws.
8 – 6 = 2
Thus Each student will get 2 toothpicks more than the straws.
Question 13.
Explain how a multiplication fact can help you solve 30 ÷ 3 = _____.
Answer: 10 × 3 = 30
Explanation:
The multiplication fact to help you to solve 30 ÷ 3 is 10 × 3.
By using the multiplication fact you can get the solution for 30 ÷ 3 = 10
Relate Multiplication and Division Homework & Practice 4.2
Use the array to complete the equations
Question 1.

2 × ___ = 8
8 ÷ 2 = _____
Answer: 4
Explanation:
Number of counters = 8
Number of rows = 2
8 ÷ 2 = 4
2 × x = 8
x = 8/2
x = 4
Question 2.

3 × ____ = 9
9 ÷ 3 = ____
Answer: 3
Explanation:
Number of counters = 9
Number of rows = 3
3 × x = 9
x = 9/3
x = 3
9 ÷ 3 = 3
Question 3.
Draw an array to find 5 × 7. Write the other 3 facts in the fact family.
5 × 7 = _____
___________
___________
___________
Answer: 35
Explanation:
The other 3 facts are
5 × 7 = 35
7 × 5 = 35
35 ÷ 5 = 7
35 ÷ 7 = 5
Complete the fact family
Question 4.

Answer: 1, 9
Explanation:
9 × 1 = 9
9 ÷ 1 = 9
1 × 9 = 9
9 ÷ 9 = 1
Question 5.

Answer: 7, 6
Explanation:
6 × 7 = 42
42 ÷ 7 = 6
7 × 6 = 42
42 ÷ 6 = 7
Write the fact family for the numbers.
Question 6.
4, 8, 32
Answer: 8 × 4 = 32, 32 ÷ 4 = 8, 32 ÷ 8 = 4
Explanation:
The facts family for the numbers are
4 × 8 = 32
8 × 4 = 32
32 ÷ 8 = 4
32 ÷ 4 = 8
Question 7.
6, 7, 42
Answer: 6 × 7 = 42, 42 ÷ 6 = 7, 42 ÷ 7 = 6
Explanation:
The facts family for the numbers are
6 × 7 = 42
7 × 6 = 42
42 ÷ 7 = 6
42 ÷ 6 = 7
Question 8.
Which One Doesn’t Belong?
Which equation does not belong with the other three?
3 × 7 = 21
7 × 3 = 21
21 ÷ 7 = 3
7 + 3 = 10
Answer: 7 + 3 = 10
Explanation:
The equation that does not belong to other three equation is 7 + 3 = 10.
Question 9.
DIG DEEPER!
Newton has 16 pennies. He wants to put them in stacks that are the same height. How many stacks does he make?

Answer: 2
Explanation:
Given,
Newton has 16 pennies. He wants to put them in stacks that are the same height.
16 ÷ 8 = 2
Thus he makes 2 stacks.
Question 10.
Modeling Real Life
Your art teacher divides the items shown equally among 6 students. Write two equations that you can use to show how many pieces of paper each student gets.
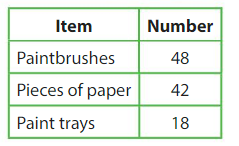
Answer:
Given
Your art teacher divides the items shown equally among 6 students.
48 ÷ 6 = 8 paintbrushes
42 ÷ 6 = 7 pieces of paper
Thus each student gets 7 pieces of paper.
Question 11.
Modeling Real Life
Use the table above to find how many more paintbrushes students will get than paint trays.
Answer:
Your art teacher divides the items shown equally among 6 students.
18 ÷ 6 = 3 paint trays
48 ÷ 6 = 8 paintbrushes
8 – 3 = 5
Thus the students will get 5 more paintbrushes than paint trays.
Review & Refresh
Find the missing factor.
Question 12.
5 × ____ = 45
Answer: 9
Explanation:
Let the missing factor be g.
5 × g = 45
g = 45/5
g = 9
Thus the missing factor is 9.
Question 13.
2 × ____ = 16
Answer: 8
Explanation:
Let the missing factor be h.
2 × h = 16
h = 16/2
h = 8
Thus the missing factor is 8.
Question 14.
_____ × 2 = 4
Answer: 2
Explanation:
Let the missing factor be i.
i × 2 = 4
i = 4/2
i = 2
Thus the missing factor is 2.
Question 15.
____ × 3 = 15
Answer: 5
Explanation:
Let the missing factor be j.
j × 3 = 15
j = 15/3
j = 5
Thus the missing factor is 5.
Question 16.
5 × ____ = 10
Answer: 2
Explanation:
Let the missing factor be k.
5 × k = 10
k = 10/5
k = 2
Thus the missing factor is 2.
Question 17.
5 × ____ = 5
Answer: 1
Explanation:
Let the missing factor be l.
5 × l = 5
l = 5/5
l = 1
Thus the missing factor is 1.
Lesson 4.3 Divide by 2, 5, or 10
Explore and Grow
Use the number line to model 10 ÷ 2.
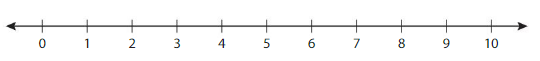
10 ÷ 2 = _____
Answer: 5
Structure
In your number line model, does 2 represent the number of equal groups or the size of the groups? Explain.
Answer: Yes, the number line model 2 represents the number of equal groups or the size of the groups.
Think and Grow: Divide by 2, 5, or 10
Example
Find 16 ÷ 2.

Answer:
Number of rows = 2
Number of counters = 16
Division equation is 16 ÷ 2 = 8
Multiplication equation is 2 × 8 = 16
Example
Find 20 ÷ 5.
Think: 5 times what number is 20?
5 × ____ = 20
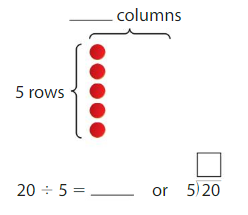
Answer:
Number of rows = 5
Number of counters = 20
Division equation is 20 ÷ 5 = 4
Multiplication equation is 5 × 4 = 20
Example
Find 30 ÷ 10.
Think: 10 times what number is 30?
10 × _____ = 30
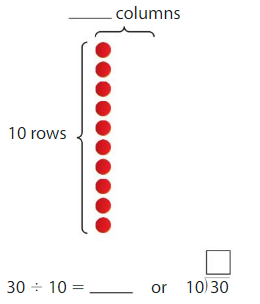
Answer:
Number of rows = 10
Number of counters = 30
Division equation is 30 ÷ 10 = 3
Multiplication equation is 10 × 3 = 30
Show and Grow
Write the related multiplication fact. Then find the quotient
Question 1.
Find 60 ÷ 10.
10 × ____ = 60
60 ÷ 10 = ____
Answer: 6, 6
Explanation:
The related multiplication fact for 60 and 10 is
10 × x = 60
x = 60/10
x = 6
60 ÷ 10 = 6
Thus the quotient is 6.
Question 2.
Find 14 ÷ 2
2 × ____ = 14
14 ÷ 2 = _____
Answer: 7, 7
Explanation:
The related multiplication fact for 14 and 2 is
2 × x = 14
x = 14/2
x = 7
14 ÷ 2 = 7
Thus the quotient is 7.
Question 3.
Find 35 ÷ 5
5 × ___ = 35
35 ÷ 5 = ____
Answer: 7, 7
Explanation:
The related multiplication fact for 5 and 35 is
5 × x = 35
x = 35/5
x = 7
35 ÷ 5 = 7
Thus the quotient is 7.
Write the related multiplication fact. Then find the quotient
Question 4.
Find 4 ÷ 2.
2 × ____ = 4
4 ÷ 2 = ____
Answer: 2, 2
Explanation:
The related multiplication fact for 2 and 4 is
2 × x = 4
x = 4/2
x = 2
4 ÷ 2 = 2
Thus the quotient is 2.
Question 5.
Find 15 ÷ 5.
5 × ____ = 15
15 ÷ 5 = ____
Answer: 3, 3
Explanation:
The related multiplication fact for 5 and 15 is
5 × x = 15
x = 15/5
x = 3
15 ÷ 5 = 3
Thus the quotient is 3.
Question 6.
Find 10 ÷ 10.
10 × ____ = 10
10 ÷ 10 = ____
Answer: 1, 1
Explanation:
The related multiplication fact for 10 and 10 is
10 × x = 10
x = 10/10
x = 1
10 ÷ 10 = 1
Thus the quotient is 1.
Find the quotient
Question 7.
70 ÷ 10 = _____
Answer: 7
Divide both the numbers 70 and 10
70/10 = 7
Thus 7 is the quotient.
Question 8.
25 ÷ 5 = _____
Answer: 5
Divide both the numbers 25 and 5.
25/5 = 5
Thus 5 is the quotient.
Question 9.
18 ÷ 2 = ____
Answer: 6
Divide both the numbers 18 and 2.
18/2 = 9
Thus 9 is the quotient.
Question 10.
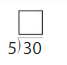
Answer: 6
Divide both the numbers 30 and 5.
30/5 = 6
Thus 6 is the quotient.
Question 11.
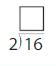
Answer: 8
Divide both the numbers 16 and 2.
16/2 = 8
Thus 8 is the quotient.
Question 12.
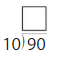
Answer: 9
Divide both the numbers 10 and 90.
90/10 = 9
Thus 9 is the quotient.
Question 13.
Divide 60 by 10.
Answer: 6
Divide both the numbers 60 and 10.
60/10 = 6
Thus 6 is the quotient.
Question 14.
Divide 14 by 2.
Answer: 7
Divide both the numbers 2 and 14.
14/2 = 7
Thus 7 is the quotient.
Question 15.
Divide 45 by 5.
Answer: 9
Divide both the numbers 45 and 5.
45/5 = 9
Thus 9 is the quotient.
Find the missing divisor.
Question 16.
12 ÷ ____ = 6
Answer: 2
Explanation:
Let the missing divisor is x
12 ÷ x = 6
12/x = 6
12 = 6 × x
x = 12/6
x = 2
Thus the missing divisor is 2.
Question 17.
10 ÷ ____ = 2
Answer: 5
Explanation:
Let the missing divisor is y
10 ÷ y = 2
10/y = 2
10 = 2 × y
y = 10/2
y = 5
Thus the missing divisor is 5.
Question 18.
50 ÷ ____ = 5
Answer: 10
Explanation:
Let the missing divisor is z.
50 ÷ z = 5
50/z = 5
50 = 5 × z
z = 50/5
z = 10
Thus the missing divisor is 10.
Question 19.
You make 2 batches of pancakes. You use 6 cups of flour. How many cups of flour are in 1 batch?

Answer: 3
Explanation:
Given that,
You make 2 batches of pancakes.
You use 6 cups of flour.
6/2 = 3 cups of flour
There are 3 cups of flour in 1 batch.
Question 20.
DIG DEEPER!
I am an even number. If you multiply me by 5, then divide the product by 10, the quotient is 2. What number am I?
Answer: 20
Explanation:
I am an even number. If you multiply me by 5, then divide the product by 10, the quotient is 2.
Let 4 be the even number.
4 × 5 = 20
20/10 = 2
Thus the number is 4.
Think and Grow: Modeling Real Life
Fourteen students say a dog is their favorite pet. How many symbols should you draw to complete the picture graph?

Division equation:
You should draw _____ symbols
Answer:
Given,
Fourteen students say a dog is their favorite pet.

???? = 2 students
14 ÷ 2 = 7 pictures
Show and Grow
Question 21.
Twenty-five students say riding a bike is their favorite summer activity. How many symbols should you draw to complete the picture graph?

Answer:
Given,
Twenty-five students say riding a bike is their favorite summer activity.
???? = 5 students
25 = ???? ????????????????
25 ÷ 5 = 5
Question 22.
Erasers cost 10¢ each. How many erasers can you buy with 70¢?
Answer:
Given that,
Erasers cost 10¢ each.
You need to buy with 70¢
10 × x = 70
x = 70/10
x = 7
Therefore you can buy 7 erasers for 70¢.
Question 23.
You have 26 red linking cubes and 24 blue linking cubes. You use all of the linking cubes to make towers with 10 linking cubes each. How many towers do you make?
Answer: 5
Explanation:
Given that,
You have 26 red linking cubes and 24 blue linking cubes.
26 + 24 = 50 linking cubes
You use all of the linking cubes to make towers with 10 linking cubes each.
50 ÷ 10 = 5 towers
Thus you can make 5 towers.
Divide by 2, 5, or 10 Homework & Practice 4.3
Write the related multiplication fact. Then find the quotient.
Question 1.
Find 20 ÷ 10
10 × ____ = 20
20 ÷ 10 = ____
Answer: 2, 2
Explanation:
Let x be the unknown factor.
10 × x = 20
x = 20/10
x = 2
First, we need to check whether the divisor or dividend is the related multiplication fact or not.
Next check whether the divisor or the dividend the product in the related multiplication fact or not.
If both are the same then the quotient is the unknown factor.
20/10 = 2
Thus the quotient is 2.
Question 2.
Find 8 ÷ 2.
2 × ___ = 8
8 ÷ 2 = ____
Answer: 4, 4
Explanation:
Let y be the unknown factor.
First, we need to check whether the divisor or dividend is the related multiplication fact or not.
Next check whether the divisor or the dividend the product in the related multiplication fact or not.
If both are the same then the quotient is the unknown factor.
2 × y = 8
y = 8/2
y = 4
Thus the quotient is 4.
Question 3.
Find 50 ÷ 5
5 × ___ = 50
50 ÷ 5 = ____
Answer: 10, 10
Explanation:
Let z be the unknown factor.
First, we need to check whether the divisor or dividend is the related multiplication fact or not.
Next check whether the divisor or the dividend the product in the related multiplication fact or not.
If both are the same then the quotient is the unknown factor.
5 × z = 50
z = 50/5
z = 10
Thus the quotient is 10.
Find the quotient
Question 4.
100 ÷ 10 = _____
Answer: 10
Explanation:
100/10 = 10
The quotient is 10.
Question 5.
45 ÷ 5 = _____
Answer: 9
Explanation:
45/5 = 9
The quotient is 9.
Question 6.
14 ÷ 2 = _____
Answer: 7
Explanation:
14/2 = 7
The quotient is 7.
Question 7.

Answer: 6
Explanation:
12/2 = 6
The quotient is 6.
Question 8.

Answer: 6
Explanation:
60/10 = 6
The quotient is 6.
Question 9.
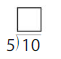
Answer: 2
Explanation:
10/5 = 2
The quotient is 2.
Find the missing divisor
Question 10.
20 ÷ ___ = 5
Answer: 4
Explanation:
Let x be the missing divisor
20 ÷ x = 5
20/x = 5
20 = x × 5
x = 20/5
x = 4
Thus the missing divisor is 4.
Question 11.
40 ÷ ____ = 10
Answer: 4
Explanation:
Let x be the missing divisor.
40 ÷ x = 10
40/x = 10
40 = 10 × x
x = 40/10
x = 4
Thus the missing divisor is 4.
Question 12.
4 ÷ ____ = 2
Answer: 2
Explanation:
Let x be the missing divisor.
4 ÷ x = 2
4/x = 2
4 = 2 × x
x = 4/2
x = 2
Thus the missing divisor is 2.
Question 13.
Number Sense
The American flag has 50 stars. It has 10 times as many stars as the Chinese flag. How many stars are on the Chinese flag?
Answer:
Given,
The American flag has 50 stars. It has 10 times as many stars as the Chinese flag.
50/10 = 5
Thus there are 5 stars on the Chinese flag.
Question 14.
Open-Ended Write a division equation for each description.

Answer: 10 ÷ 2 = 5
In this equation 2 is the divisor, 5 is the quotient and 10 is the dividend.
Question 15.
Repeated Reasoning
Complete the table.
Answer:
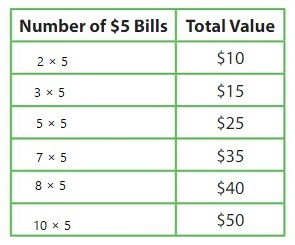
Question 16.
You buy 20 flowers. You want an equal number of flowers in each of the 5 pots. How many flowers do you put in each pot?

Answer:
Given,
You buy 20 flowers. You want an equal number of flowers in each of the 5 pots.
20/5 = 4
Thus there are 4 flowers in each pot.
Question 17.
Modeling Real Life
Fifty students say they have traveled on an airplane. How many symbols should you draw to complete the picture graph?

Answer:
Given that,
Fifty students say they have traveled on an airplane.
???? = 10 students
50 = 10 × 5
= ???? × 5

Question 18.
Modeling Real Life
A jeweler has 17 gold rings and 18 silver rings. She puts them in a ring tray in 5 rows. How many rings are in each row?
Answer: 7 rings
Explanation:
Given that,
A jeweler has 17 gold rings and 18 silver rings.
17 + 18 = 35
She puts them in a ring tray in 5 rows.
35/5 = 7
Therefore there are 7 rings in each row.
Review & Refresh
Compare.
Question 19.

Answer: >
Explanation:
8 × 3 = 24
7 × 3 = 21
24 > 21
So, 8 × 3 > 7 × 3
Question 20.
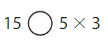
Answer: =
Explanation:
5 × 3 = 15
15 = 15
So, 15 = 5 × 3
Question 21.
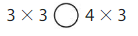
Answer: <
Explanation:
3 × 3 = 9
4 × 3 = 12
9 < 12
So, 3 × 3 < 4 × 3
Lesson 4.4 Divide by 3 or 4
Explore and Grow
Put 12 counters into 3 equal groups. Draw to show your groups.
Use your equal groups to help you find the quotient.
12 ÷ 3 = ____
Answer: 4

Structure
Put 12 counters into 4 equal groups. Draw to show your groups. Write a division equation to match. What do you notice?
Answer: 3
Think and Grow: Divide by 3 or 4
Example
Find 18 ÷ 3
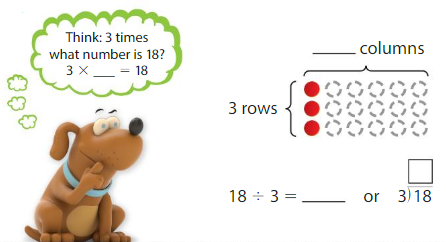
Answer: 6
Explanation:
Let the unknown number be x.
18 ÷ 3 = x
18/3 = x
x = 6
Thus 18 is 3 times 6.
Example
Find 32 ÷ 4.
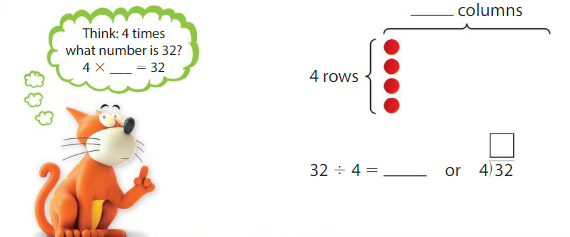
Answer: 8
Explanation:
Let the unknown number be x.
32 ÷ 4 = x
32/4 = x
x = 8
Thus 32 is 4 times 8.
4 × 8 = 32
Show and Grow
Complete the model and find the quotient.
Question 1.
Find 28 ÷ 4.
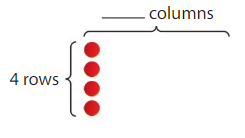
28 ÷ 4 = _____
Answer: 7
Explanation:
Number of rows = 4
Number of counters = 28
Divide the number of counters by the number of rows
28/4 = 7
Thus there are 7 columns in each row.
Question 2.
Find 9 ÷ 3.
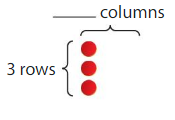
9 ÷ 3 = _____
Answer: 3
Explanation:
Number of rows = 3
Number of counters = 9
Divide the number of counters by the number of rows
9/3 = 3
Thus there are 3 columns in each row.
Apply and Grow: Practice
Complete the model and find the quotient.
Question 3.
Find 8 ÷ 4.
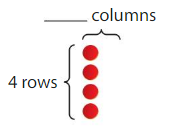
8 ÷ 4 = _____
Answer: 2
Explanation:
Number of rows = 4
Number of counters = 8
Divide the number of counters by the number of rows
8/4 = 2
Thus there are 2 columns in each row.
Question 4.
Find 24 ÷ 3.
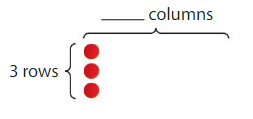
24 ÷ 3 = _____
Answer: 8
Explanation:
Number of rows = 3
Number of counters = 24
Divide the number of counters by the number of rows
24/3 = 8
Thus there are 8 columns in each row.
Find the quotient
Question 5.
12 ÷ 3 = _____
Answer: 4
Explanation:
Divide the two numbers 12 and 3.
12/3 =4
Thus the quotient is 4
Question 6.
20 ÷ 4 = _____
Answer: 5
Explanation:
Divide the two numbers 20 and 4.
20/4 = 5
Thus the quotient is 5.
Question 7.
15 ÷ 3 = _____
Answer: 5
Explanation:
Divide the two numbers 15 and 3
15/3 = 5
Thus the quotient is 5.
Question 8.
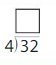
Answer: 8
Explanation:
Divide the two numbers 32 and 4
32/4 = 8
Thus the quotient is 8.
Question 9.

Answer: 6
Explanation:
Divide the two numbers 3 and 18
18/3 = 6
Thus the quotient is 6.
Question 10.

Answer: 9
Explanation:
Divide the two numbers 36 and 4
36/4 = 9
Thus the quotient is 9.
Question 11.
Divide 9 by 3.
Answer: 3
Explanation:
Divide the two numbers 3 and 9
9/3 = 3
Thus the quotient is 3.
Question 12.
Divide 12 by 4.
Answer: 3
Explanation:
Divide the two numbers 12 and 4.
12/4 = 3
Thus the quotient is 3.
Question 13.
Divide 21 by 3.
Answer: 7
Explanation:
Divide the two numbers 21 by 3
21/3 = 7
Thus the quotient is 7.
Compare
Question 14.
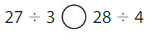
Answer: >
Explanation:
Divide the two numbers.
27 ÷ 3 = 9
28 ÷ 4 = 7
9 > 7
27 ÷ 3 > 28 ÷ 4
Question 15.
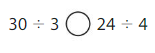
Answer: >
Explanation:
Divide the two numbers
30 ÷ 3 =10
24 ÷ 4 = 6
10 > 6
30 ÷ 3 > 24 ÷ 4
Question 16.

Answer: <
Explanation:
Divide the two numbers
6 ÷ 3 = 2
16 ÷ 4 = 4
2 < 4
6 ÷ 3 < 16 ÷ 4
Question 17.
There are 36 water bottles in a package. The bottles are in 4 rows. How many water bottles are in each row?
Answer: 9
Explanation:
Given,
There are 36 water bottles in a package.
The bottles are in 4 rows.
36/4 = 9
Thus 9 water bottles are in each row.
Question 18.
DIG DEEPER!
Can you divide 20 students into 3 equal groups? Explain.
Answer: No
20 is not the multiple of 3. So, 20 students cannot be divided into 3 equal groups.
Think and Grow: Modeling Real Life
You arrange 36 chairs in 4 equal rows. You arrange 21 music stands in 3 equal rows. How many more chairs are in each row than music stands?

Division equations:
There are ______ more chairs in each row.
Answer:
Given,
You arrange 36 chairs in 4 equal rows.
36/4 = 9 chairs in each row
You arrange 21 music stands in 3 equal rows.
21/3 = 7 chairs in each row
Thus there are 2 more chairs in each row.
Show and Grow
Question 19.
You arrange 30 cups of fruit punch in 3 equal rows. You arrange 24 cups of lemonade in 4 equal rows. How many more cups of fruit punch are in each row than cups of lemonade?
Answer:
Given,
You arrange 30 cups of fruit punch in 3 equal rows.
30/3 = 10 cups of fruit punch
You arrange 24 cups of lemonade in 4 equal rows.
24/4 = 6 cups of lemonade
10 > 6
Thus 4 more cups of fruit punch are in each row than cups of lemonade.
Question 20.
You have a bag of 25 carrot sticks. You eat 5 of them and equally share the rest with 4 friends. How many carrot sticks does each friend get?

Answer: 5
Explanation:
Given that,
You have a bag of 25 carrot sticks. You eat 5 of them and equally share the rest with 4 friends.
25 – 5 = 20 carrot sticks
20/4 = 5 carrot sticks
Thus each friend gets 5 carrot sticks.
Question 21.
Your teacher has 18 yellow pencils and 18 red pencils. She puts 3 pencils on each desk in the class. How many desks are in the class?
Answer: 12
Explanation:
Given that,
Your teacher has 18 yellow pencils and 18 red pencils.
18 + 18 = 36 pencils
She puts 3 pencils on each desk in the class.
36/3 = 12
Thus there are 12 desks in the class.
Divide by 3 or 4 Homework & Practice 4.4
Complete the model and find the quotient
Question 1.
Find 27 ÷ 3
27 ÷ 3 = ______
Answer: 9
Explanation:
Number of rows = 3
Number of counters = 27
Divide the number of counters by the number of rows
27/3 = 9
Thus there are 9 counters in each row.
Question 2.
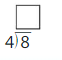
Find 20 ÷ 4.
20 ÷ 4 _____
Answer: 5
Explanation:
Number of rows = 4
Number of counters = 20
Divide the number of counters by the number of rows
20/4 = 5
Thus there are 5 counters in each row.
Find the quotient
Question 3.
6 ÷ 3 = _____
Answer: 2
Explanation:
Divide the two numbers 3 and 6.
6/3 = 2
Thus the quotient is 2.
Question 4.
28 ÷ 4 = _____
Answer: 7
Explanation:
Divide the two numbers 28 and 4.
28/4 = 7
Thus the quotient is 7.
Question 5.
18 ÷ 3 = _____
Answer: 6
Explanation:
Divide the two numbers 18 and 3.
18/3 = 6
Thus the quotient is 6.
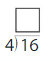
Question 6.
Answer: 2
Explanation:
Divide the two numbers 4 and 8.
8/4 = 2
Thus the quotient is 2.
Question 7.

Answer: 8
Explanation:
Divide the two numbers 24 and 3
24/3 = 8
Thus the quotient is 8.
Question 8.
Answer: 4
Explanation:
Divide the two numbers 16 and 4.
16/4 = 4
Thus the quotient is 4.
Compare
Question 9.
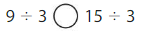
Answer: <
Explanation:
Divide the two numbers.
9 ÷ 3 = 3
15 ÷ 3 = 5
3 < 5
So, 9 ÷ 3 < 15 ÷ 3
Question 10.
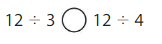
Answer: <
Explanation:
Divide the two numbers.
12 ÷ 3 = 4
12 ÷ 4 = 3
4 > 3
12 ÷ 3 > 12 ÷ 4
Question 11.

Answer: <
Explanation:
Divide the two numbers.
32 ÷ 4 = 8
36 ÷ 4 = 9
8 < 9
32 ÷ 4 < 36 ÷ 4
Question 12.
Number Sense
Tissue boxes are sold in packs of 3. A doctor’s office needs 21 boxes. How many packs should the office buy?
Answer: 7
Explanation:
Given that,
Tissue boxes are sold in packs of 3.
A doctor’s office needs 21 boxes.
21/3 = 7 packs
Therefore the office should buy 7 packs.
Question 13.
Structure
Write the division equation represented by the number line.
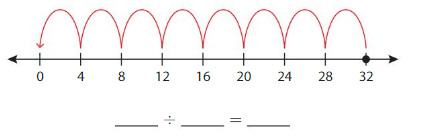
Answer: 32 ÷ 4 = 8
Explanation:
The count starts from 0.
The count jumps for every 4s.
There are 8 jumps.
Thus the division equation is 32 ÷ 4 = 8
Question 14.
YOU BE THE TEACHER
Your friend says she can use 3 × 6 = 18 to help find 6 ÷ 3. Is your friend correct? Explain.
Answer: Your friend is incorrect
Explanation:
Your friend says she can use 3 × 6 = 18 to help find 6 ÷ 3.
6 ÷ 3 = 2
The multiplication equation is different from the division equation.
By this, you can say that your friend is incorrect.
Question 15.
Modeling Real Life
A food vending machine has 40 snacks in rows of 4. A drink vending machine has 21 drinks in rows of 3. How many more rows of snacks are there than rows of drinks?
Answer:
Given,
A food vending machine has 40 snacks in rows of 4.
40/4 = 10
A drink vending machine has 21 drinks in rows of 3.
21/3 = 7
10 – 7 = 3
Thus 3 more rows of snacks are there than rows of drinks.
Question 16.
Modeling Real Life
A delivery person has 13 large packages and 14 small packages. He delivers 3 packages to each house. There are none left. How many houses does he deliver to?

Answer: 9
Explanation:
Given,
A delivery person has 13 large packages and 14 small packages.
13 + 14 = 27
He delivers 3 packages to each house. There are none left.
27/3 = 9
Thus he delivers 9 houses.
Review & Refresh
Find the product
Question 17.
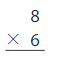
Answer: 48
Explanation:
Multiply the two numbers 8 and 6.
8 × 6 = 48
Question 18.
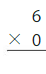
Answer: 0
Explanation:
Multiply the two numbers 6 and 0.
Any number multiplied by 0 will be always 0.
6 × 0 = 0
Question 19.
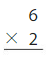
Answer: 12
Explanation:
Multiply the two numbers 6 and 2.
6 × 2 = 12
Question 20.
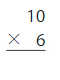
Answer: 60
Explanation:
Multiply the two numbers 10 and 6.
10 × 6 = 60
Question 21.
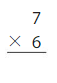
Answer: 42
Explanation:
Multiply the two numbers 7 and 6.
7 × 6 = 42
Lesson 4.5 Divide by 6 or 7
Explore and Grow
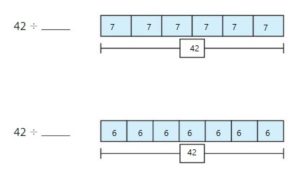
Complete the statements and the models.
Answer: 42 ÷ 6 = 7
Reasoning
Without solving, which quotient is greater? Explain how you know.
Answer: The second figure is having a greater quotient.
42 ÷ 6 = 7
42 ÷ 7 = 6
Think and Grow: Divide by 6 or 7
Example
Find 48 ÷ 6.
Think: 6 times what number is 48?
6 × _____ = 48
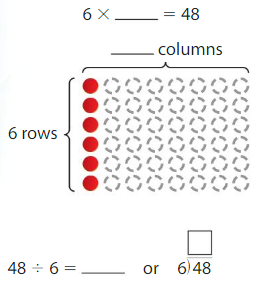
Answer: 8
Explanation:
Number of rows = 6
Number of counters = 48
Divide the number of counters by the number of rows.
48/6 = 8
There are 8 columns.
6 × 8 = 48
Example
Find 49 ÷ 7.
Think: 7 times what number is 49?
7 × ____ = 49
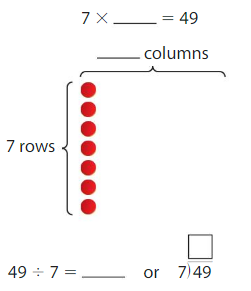
Answer: 7
Explanation:
Number of rows = 7
Number of counters = 49
Divide the number of counters by the number of rows
49/7 = 7
There are 7 columns.
7 × 7 = 49
Show and Grow
Complete the model and find the quotient
Question 1.
Find 28 ÷ 7.
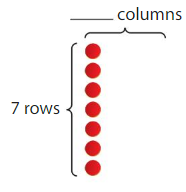
28 ÷ 7 = _____
Answer: 4
Explanation:
Number of rows = 7
Number of counters = 28
Divide the number of counters by the number of rows
28/7 = 4
There are 4 columns.
Question 2.
Find 54 ÷ 6.
54 ÷ 6 = _____
Answer: 9
Explanation:
Number of rows = 6
Number of counters = 54
Divide the number of counters by the number of rows
54/6 = 9
There are 9 columns.
Apply and Grow: Practice
Complete the model and find the quotient
Question 3.
Find 36 ÷ 6.

36 ÷ 6 = _____
Answer: 6
Explanation:
Number of rows = 6
Number of counters = 36
Divide the number of counters by the number of rows
36/6 = 6
There are 6 columns.
Question 4.
Find 14 ÷ 7.
14 ÷ 7 = _____
Answer: 2
Explanation:
Number of rows = 7
Number of counters = 14
Divide the number of counters by the number of rows
14/7 = 2
There are 2 columns.
Find the quotient
Question 5.
60 ÷ 6 = _____
Answer: 10
Explanation:
Divide the two numbers 60 and 6.
60/6 = 10
Thus the quotient is 10.
Question 6.
35 ÷ 7 = _____
Answer: 5
Exp7lanation:
Divide the two numbers 35 and 7.
35/7 = 5
Thus the quotient is 5.
Question 7.
24 ÷ 6 = _____
Answer: 4
Explanation:
Divide the two numbers 24 and 6.
24/6 = 4
Thus the quotient is 4.
Question 8.
Answer: 2
Explanation:
Divide the two numbers 12 and 6.
12/6 = 2
Thus the quotient is 2.
Question 9.

Answer: 6
Explanation:
Divide the two numbers 42 and 7.
42/7 = 6
Thus the quotient is 6.
Question 10.

Answer: 9
Explanation:
Divide the two numbers 63 and 7
63/7 = 9
Thus the quotient is 9.
Find the missing divisor
Question 11.
28 ÷ ____ = 7
Answer: 4
Explanation:
Let the missing divisor be a.
28 ÷ a = 7
28/a = 7
28 = 7a
a = 28/7
a = 4
Thus the missing divisor is 4.
Question 12.
30 ÷ ____ = 6
Answer: 5
Explanation:
Let the missing divisor be b.
30 ÷ b = 6
30/b = 6
30 = 6 × b
b = 30/6
b = 5
Thus the missing divisor is 5.
Question 13.
70 ÷ _____ = 7
Answer: 10
Explanation:
Let the missing divisor be c.
70 ÷ c = 7
70/c = 7
70 = 7 × c
c = 70/7
c = 10
Thus the missing divisor is 10.
Question 14.
You have 24 stones for the game mancala. There are 6 holes on the board. Each hole gets an equal number of stones. How many stones do you put in each hole?
Answer: 4
Explanation:
Given that,
You have 24 stones for the game mancala.
There are 6 holes on the board.
Each hole gets an equal number of stones.
24/6 = 4
Thus you put 4 stones in each hole.
Question 15.
Number Sense
Write the correct symbol to make each equation true
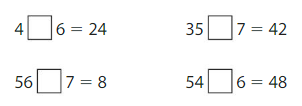
Answer:
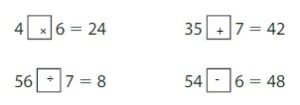
Think and Grow: Modeling Real Life
You have 54 craft sticks. You use all of the sticks to make hexagons. How many hexagons can you make?

Division equation:
You can make _____ hexagons.
Answer:
Given,
You have 54 craft sticks. You use all of the sticks to make hexagons.
hexagon – 6
54/6 = 9
You can make 9 hexagons.
Show and Grow
Question 16.
You use 35 craft sticks to make 7 polygons. You use the same number of craft sticks for each polygon. How many craft sticks do you use for each polygon?
Answer: 5
Explanation:
Given,
You use 35 craft sticks to make 7 polygons. You use the same number of craft sticks for each polygon.
35/7 = 5
Thus you use 5 craft sticks for each polygon.
Question 17.
There are 42 students in gym class. The teacher divides the students into 7 teams. How many more students would be on each team if the teacher divides the students into 6 teams?
Answer:
Given that,
There are 42 students in gym class. The teacher divides the students into 7 teams.
42/7 = 6 students
If the teacher divides the students into 6 teams then,
42/6 = 7 students
Question 18.
You have a tray of 12 oatmeal bars. You keep 6 of them. How many bars can you give to each of your 6 friends?
Answer:
Given that,
You have a tray of 12 oatmeal bars. You keep 6 of them.
12/6 = 2
Thus you can give 2 bars to each of your 6 friends.
Divide by 6 or 7 Homework & Practice 4.5
Complete the model and find the quotient
Question 1.
Find 18 ÷ 6
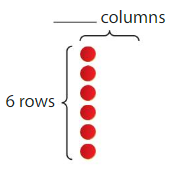
18 ÷ 6 = _____
Answer: 3
Explanation:
Number of rows = 6
Number of counters = 18
Divide the number of counters by the number of rows
18/6 = 3
Thus there are 3 counters in each row
Question 2.
Find 35 ÷ 7
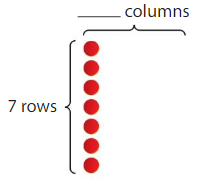
35 ÷ 7 = _____
Answer: 5
Explanation:
Number of rows = 7
Number of counters = 35
Divide the number of counters by the number of rows
35/7 = 5
Thus there are 5 counters in each row
Find the quotient
Question 3.
42 ÷ 6 = _____
Answer: 7
Explanation:
Divide the two numbers 42 and 6.
42/6 = 7
Thus the quotient is 7.
Question 4.
28 ÷ 7 = _____
Answer: 4
Explanation:
Divide the two numbers 28 and 7
28/7 = 4
Thus the quotient is 4.
Question 5.
54 ÷ 6 = _____
Answer: 9
Explanation:
Divide the two numbers 54 and 6.
54/6 = 9
Thus the quotient is 9.
Question 6.

Answer: 7
Explanation:
Divide the two numbers 49 and 7.
49/7 = 7
Thus the quotient is 7.
Question 7.

Answer: 10
Explanation:
Divide the two numbers 7 and 70
70/7 = 10
Thus the quotient is 10.
Question 8.

Answer: 5
Explanation:
Divide the two numbers 30 and 6.
30/6 = 5
Thus the quotient is 5.
Find the missing divisor.
Question 9.
36 ÷ ____ = 6
Answer: 9
Explanation:
Let the missing divisor be x.
36 ÷ x = 6
36/x = 6
36 = 6 × x
x = 36/6
x = 6
Thus the missing divisor is 6.
Question 10.
14 ÷ ____ = 7
Answer: 2
Explanation:
Let the missing divisor be y.
14 ÷ y = 7
14/y = 7
14 = 7 × y
y = 14/7
y = 2
Thus the missing divisor is 2.
Question 11.
60 ÷ _____ = 6
Answer: 10
Explanation:
Let the missing divisor be z.
60 ÷ z = 6
60/z = 6
60 = 6 × z
z = 60/6
z = 10
Thus the missing divisor is 10.
Question 12.
Number Sense
There are 7 continents. A scientist has 63 days to spend studying on all the continents. She wants to spend an equal number of days on each one. How many days can she spend on each continent?
Answer: 9
Explanation:
Given,
There are 7 continents. A scientist has 63 days to spend studying on all the continents.
She wants to spend an equal number of days on each one.
63/7 = 9 days
Thus she can spend 9 days on each continent.
Question 13.
Logic
I am an odd number. When you multiply me by 6, then divide the product by 3, the quotient is 10. What number am I?
Answer: 5
Explanation:
Let us consider 5 to be the odd number.
Now multiply by 6.
5 × 6 = 30
Now divide by 3.
30/3 = 10
So, the number is 5.
Question 14.
DIG DEEPER!
You deal 52 cards to 7 players. Does each player get the same number of cards? Explain.

Answer: No. Because 52 is not the multiple of 7.
Thus each player will not get the same number of cards.
Question 15.
Modeling Real Life
There are 70 students at a summer camp. A counselor divides the students into teams of 10. How many more teams would the counselor make if he divides the students into teams of 7?
Answer:
Given,
There are 70 students at a summer camp. A counselor divides the students into teams of 10.
If he divides into 7 teams then there will be 10 students in each team.
70/7 = 10
Question 16.
Modeling Real Life
There are 31 students in your class. Seven students are called to the nurse’s office to get their hearing checked. Your teacher divides the rest of the students into groups of 6. How many groups are there?
Answer:
Given that,
There are 31 students in your class. Seven students are called to the nurse’s office to get their hearing checked.
31 – 7 = 24
Your teacher divides the rest of the students into groups of 6.
24/6 = 4 groups
Thus there are 4 groups.
Review & Refresh
Find the product
Question 17.
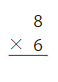
Answer: 48
Explanation:
Multiply the two numbers 8 and 6.
8 × 6 = 48
Question 18.
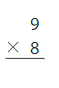
Answer: 72
Explanation:
Multiply the two numbers 9 and 8.
9 × 8 = 72
Question 19.
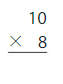
Answer: 80
Explanation:
Multiply the two numbers 10 and 8.
10 × 8 = 80
Question 20.
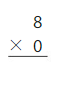
Answer: 0
Explanation:
Multiply the two numbers 0 and 8.
Any number multiplied by 0 will be always 0.
Thus 8 × 0 = 0
Question 21.
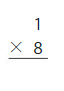
Answer: 8
Explanation:
Multiply the two numbers 1 and 8.
Any number multiplied by 1 will be always the same number.
So, 1 × 8 = 8
Lesson 4.6 Divide by 8 or 9
Explore and Grow
Use repeated subtraction to find 48 ÷ 8.
Answer:
48 – 8 = 40
40 – 8 = 32
32 – 8 = 24
24 – 8 = 16
16 – 8 = 8
8 – 8 = 0
At sixth number we got 0.
So, 48/8 in repeated subtraction is 6.
Reasoning
How many times did you subtract 8 from 48? Does the quotient represent the number of groups or the size of the groups? Explain.
Answer: I subtracted 8 from 48 six times. Yes, the quotient represents the number of groups or size of the groups.
Think and Grow: Divide 8 or 9
Example
Find 40 ÷ 8.
Think: 8 times what number is 40?
8 × ____= 40
Answer: 5
Explanation:
Number of rows = 8
Number of counters = 40
Divide the number of counters by the number of rows
40/8 = 5
Thus there are 5 columns.
8 times 5 is 40.
Example
Find 54 ÷ 9.
Think: 9 times what number is 54?
9 × ____ = 54
Answer: 6
Explanation:
Number of rows = 9
Number of counters = 54
Divide the number of counters by the number of rows
54/9 = 6
Thus there are 6 columns.
9 times 6 is 54.
Show and Grow
Complete the model and find the quotient
Question 1.
24 ÷ 8 = ____
24 ÷ 8 = ____
Answer: 3
Explanation:
Number of rows = 8
Number of counters = 24
Divide the number of counters by the number of rows
24/8 = 3
There are 3 columns
8 times 3 is 24.
Question 2.
18 ÷ 9 = ____
18 ÷ 9 = ____
Answer: 2
Explanation:
Number of rows = 9
Number of counters = 18
Divide the number of counters by the number of rows
18/9 = 2
There are 2 columns
2 times 9 is 18.
Apply and Grow: Practice
Complete the model and find the quotient
Question 3.
Find 36 ÷ 9.
36 ÷ 9 = _____
Answer: 4
Explanation:
Number of rows = 9
Number of counters = 36
Divide the number of counters by the number of rows
36/9 = 4
There are 4 columns
4 times 9 is 36.
Question 4.
Find 32 ÷ 8.
32 ÷ 8 = ____
Answer: 4
Explanation:
Number of rows = 8
Number of counters = 32
Divide the number of counters by the number of rows
32/8 = 4
There are 4 columns
8 times 4 is 32.
Find the quotient
Question 5.
45 ÷ 9 = _____
Answer: 5
Explanation:
Divide the two numbers 45 and 9
45/9 = 5
Thus the quotient is 5.
Question 6.
56 ÷ 8 = _____
Answer: 7
Explanation:
Divide the two numbers 56 and 8.
56/8 = 7
Thus the quotient is 7.
Question 7.
90 ÷ 9 = ____
Answer: 10
Explanation:
Divide the two numbers 90 and 9.
90/9 = 10
Thus the quotient is 10.
Question 8.
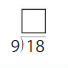
Answer: 2
Explanation:
Divide the two numbers 9 and 18
18/9 = 2
Thus the quotient is 2.
Question 9.

Answer: 6
Explanation:
Divide the two numbers 8 and 48
48/8 = 6
Thus the quotient is 6.
Question 10.
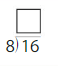
Answer: 2
Explanation:
Divide the two numbers 16 and 8.
16/8 = 2
Thus the quotient is 2.
Question 11.
Divide 54 by 9.
Answer: 6
Explanation:
Divide the two numbers 54 and 9
54/9 = 6
Thus the quotient is 6.
Question 12.
Divide 64 by 8.
Answer: 8
Explanation:
Divide the two numbers 64 and 8.
64/8 = 8
Thus the quotient is 8.
Question 13.
Divide 63 by 9
Answer: 7
Explanation:
Divide the two numbers 63 and 9
63/9 = 7
Thus the quotient is 7.
Compare
Question 14.

Answer: =
Explanation:
Divide the two numbers
81 ÷ 9 = 9
72 ÷ 8 = 9
9 = 9
So, 81 ÷ 9 = 72 ÷ 8
Question 15.
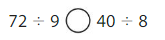
Answer: >
Explanation:
Divide the two numbers
72 ÷ 9 = 8
40 ÷ 8 = 5
8 > 5
So, 72 ÷ 9 > 40 ÷ 8
Question 16.
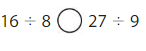
Answer: <
Explanation:
Divide the two numbers
16 ÷ 8 = 2
27 ÷ 9 = 3
2 < 3
So, 16 ÷ 8 < 27 ÷ 9
Question 17.
A comic book has 63 pages. You read 9 pages each night. How many nights will it take to read the entire book?
Answer: 7
Explanation:
Given that,
A comic book has 63 pages. You read 9 pages each night.
63/9 = 7
Thus it will take 7 nights to read the entire book.
Question 18.
Logic
Find the missing number.

Answer: 8
Explanation:
8 times 8 is 64.
Thus the missing number is 8.
Think and Grow: Modeling Real Life
There are 9 innings in a baseball game. The table shows how many innings Newton played each season. How many games has Newton played in all?
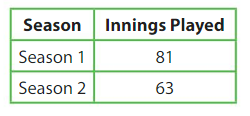
Division equation:
Newton played ______ games in all.
Answer:
Given,
There are 9 innings in a baseball game.
The table shows how many innings Newton played each season.
Season 1: 81/9 = 9 games
Season 2: 63/9 = 7 games
9 + 7 = 16 games
Therefore Newton played 16 games in all.
Show and Grow
Question 19.
The third-grade and fourth-grade classes are going on a field trip. A van can carry 8 students. How many vans are needed in all?
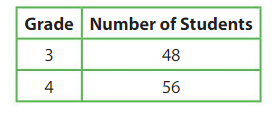
Answer:
Given that,
The third-grade and fourth-grade classes are going on a field trip.
A van can carry 8 students.
Grade 3 – 48 students
Grade 4 – 56 students
third grade – 48/8 = 6 vans
fourth grade – 56/8 = 7 vans
6 + 7 = 13 vans
Thus 13 vans are needed in all.
Question 20.
Seventy-two ballet dancers are arranged into an array with 9 columns. How many dancers are in each column?
Answer: 8 dancers
Explanation:
Given that,
Seventy-two ballet dancers are arranged into an array with 9 columns.
72/9 = 8
Thus 8 dancers are in each column.
Question 21
You make 15 paper elephants and 17 paper lions. You give all of the animals away to 8 friends. Each friend gets the same number of animals. How many animals does each friend get?

Answer: 4
Explanation:
Given that,
You make 15 paper elephants and 17 paper lions.
15 + 17 = 32
You give all of the animals away to 8 friends.
Each friend gets the same number of animals.
32/8 = 4
Thus each friend gets 4 animals.
Divide by 8 or 9 Homework & Practice 4.6
Complete the model and find the quotient
Question 1.
Find 16 ÷ 8.
16 ÷ 8 = ____
Answer: 2
Explanation:
Number of rows = 8
Number of counters = 16
Divide the number of counters by the number of rows
Division equation is 16 ÷ 8 = 2
Thus the number of columns is 2.
Question 2.
Find 45 ÷ 9.
45 ÷ 9 = _____
Answer: 5
Explanation:
Number of rows = 9
Number of counters = 45
Divide the number of counters by the number of rows
Division equation is 45 ÷ 9 = 5
Thus the number of columns is 5.
Find the quotient
Question 3.
48 ÷ 8. = _____
Answer: 6
Explanation:
Divide the two numbers 48 and 8.
48/8 = 6
Thus the quotient is 6.
Question 4.
63 ÷ 9 = ______
Answer: 7
Explanation:
Divide the two numbers 63 and 9.
63/9 = 7
Thus the quotient is 7.
Question 5.
54 ÷ 9 = _____
Answer: 6
Explanation:
Divide the two numbers 54 and 9.
54/9 = 6
Thus the quotient is 6.
Question 6.

Answer: 4
Explanation:
Divide the two numbers 32 and 8.
32/8 = 4
Thus the quotient is 4.
Question 7.
Answer: 9
Explanation:
Divide the two numbers 72 and 8.
72/8 = 9
Thus the quotient is 9.
Question 8.
Answer: 2
Explanation:
Divide the two numbers 18 and 9.
18/9 = 2
Thus the quotient is 2.
Compare
Question 9.

Answer: =
Explanation:
Divide the two numbers
90/9 = 10
80/8 = 10
10 = 10
90 ÷ 9 = 80 ÷ 8
Question 10.
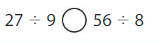
Answer: <
Explanation:
Divide the two numbers
27/9 = 3
56/8 = 7
3 < 7
27 ÷ 9 < 56 ÷ 8
Question 11.

Answer: >
Explanation:
Divide the two numbers
72 ÷ 9 = 8
40 ÷ 8 = 5
8 > 5
72 ÷ 9 > 40 ÷ 8
Question 12.
A food truck owner needs 64 whole wheat pitas. The pitas come in packages of 8. How many packages should she buy?
Answer: 8
Explanation:
Given that,
A food truck owner needs 64 whole-wheat pitas. The pitas come in packages of 8.
64 ÷ 8 = 8
Thus she should buy 8 packages.
Question 13.
Patterns
Complete the division tables.
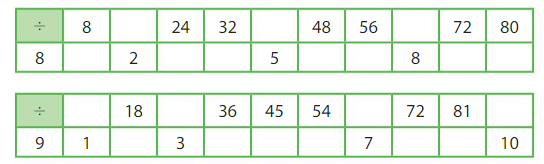
Answer:
Question 14.
Structure
Describe two different ways to find 54 ÷ 9.
Answer: 6
The different ways to find 54 ÷ 9 is a division equation and multiplication equation.
54/9 = 6
6 × 9 = 54
Question 15.
Modeling Real Life
A youth group leader is preparing for a remote-control car race. Batteries are sold in packs of 8. How many packs of batteries should he buy?
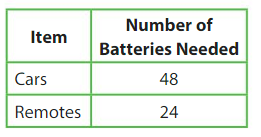
Answer:
Given,
A youth group leader is preparing for a remote-control car race.
Batteries are sold in packs of 8.
cars – 48
48 ÷ 8 = 6 batteries for cars
24 ÷ 8 = 3 batteries for remote
Question 16.
Modeling Real Life
Newton divides 32 treats equally between 8 friends. Descartes divides 27 treats equally between 9 friends. Whose friends get more treats? Explain.
Answer:
Given that,
Newton divides 32 treats equally between 8 friends.
32 ÷ 8 = 4
Descartes divides 27 treats equally between 9 friends.
27 ÷ 9 = 3
Thus Newton’s friends get more treats.
Review & Refresh
Find the missing factor.
Question 17.
____ × 4 = 0
Answer: 0
Explanation:
Let the missing factor be x.
x × 4 = 0
x = 0/4
x = 0
Thus the missing factor is 0.
Question 18.
1 × ____ = 2
Answer: 2
Explanation:
Let the missing factor be y.
1 × y = 2
y = 2/1
y = 2
Thus the missing factor is 2.
Question 19.
9 × ____ = 9
Answer: 1
Explanation:
Let the missing factor be z.
9 × z = 9
z = 9/9
z = 1
Thus the missing factor is 1.
Lesson 4.7 Divide by 0 or 1
Explore and Grow
Find the quotients

Answer:

Structure
What patterns do you notice? Use the patterns to find each quotient.
52 ÷ 52 = _____
0 ÷ 52 = _____
52 ÷ 1 = ______
Answer:
52 ÷ 52 = 1
Any number divided by the same number will be always 1.
0 ÷ 52 = 0
Any number divided by 0 will be always 0.
52 ÷ 1 = 52
Any number divided by 1 will be the same number.
Think and Grow: Divide by 0 or 1
Dividing a number by 1 or itself:
• Any number divided by1 is itself.
• Any number (except 0) divided by itself is 1.
Example
Find 7 ÷ 1.
Think: 1 time what number is 7?
1 × ____ = 7
Write: 7 × 1 = _____
Answer:
Any number divided by 1 will be the same number.
7 × 1 = 7
Example
Find 5 ÷ 5.
Think: 5 times what number is 5?
5 × ____ = 5
Write: 5 ÷ 5 = _____
Dividing with 0:
• 0 divided by any number (except 0) is 0.
• You cannot divide by 0.
Answer:
5 × 1 = 5
5 times 1 is 5.
5 ÷ 5 = 1
Example
Find 0 ÷ 8.
Think: 8 times what number is 0?
8 × ____ = 0
Write: 0 × 8 = _____
Answer:
0 times 8 is 0.
Any number multiplied by 0 is always 0.
0 × 8 = 0
Example
Find 9 ÷ 0.
Think: 0 times what number is 9?
There is no such number. So, you cannot divide by 0.
Show and Grow
Write the related multiplication fact. Then find the quotient.
Question 1.
2 ÷ 2 = _____
Answer: 1
Explanation:
The related multiplication fact for 2, 1 is
2 × 1 = 2
1 × 2 = 2
2 ÷ 2 = 1
Thus the quotient is 1.
Question 2.
0 ÷ 3 = _____
Answer: 0
Explanation:
The related multiplication fact for 0, 3 is
0 × 3 = 0
3 × 0 = 0
Thus the quotient is 0.
Question 3.
10 ÷ 1 =_____
Answer: 10
Explanation:
The related multiplication fact for 1, 10
1 × 10 = 10
10 × 1 = 10
10 ÷ 1 = 10
Thus the quotient is 10.
Question 4.
25 ÷ 25 = _____
Answer: 1
Explanation:
The related multiplication fact for 25, 1
1 × 25 = 25
25 × 1 = 25
25 ÷ 25 = 1
Thus the quotient is 1.
Apply and Grow: Practice
Write the related multiplication fact. Then find the quotient.
Question 5.
6 ÷ 1 = ______
Answer: 6
Explanation:
The related multiplication fact for 6,1
1 × 6 =6
6 × 1 = 6
6 ÷ 1 = 6
Thus the quotient is 6.
Question 6.
0 ÷ 2 = _____
Answer: 0
Explanation:
The related multiplication fact for 0,2
Any number divided by 0 will be always 0.
0 ÷ 2 = 0
Thus the quotient is 0.
Question 7.
9 ÷ 9 = ____
Answer: 1
Explanation:
The related multiplication fact for 1, 9
1 × 9 = 9
9 × 1 = 9
9 ÷ 9 = 1
Thus the quotient is 1.
Question 8.
8 ÷ 1 = _____
Answer: 8
Explanation:
The related multiplication fact for 1, 8
1 × 8 = 8
8 × 1 =8
8 ÷ 1 = 8
Thus the quotient is 8.
Find the quotient
Question 9.
5 ÷ 1 = _____
Answer: 5
Explanation:
Any number divided by 1 will be the same number.
5/1 = 5
Thus the quotient is 5
Question 10.
0 ÷ 7 = _____
Answer: 0
Explanation:
Any number divided by 0 will be always 0.
0/7 = 0
Thus the quotient is 0.
Question 11.
4 ÷ 4 = _____
Answer: 1
Explanation:
4/4 = 1
Thus the quotient is 1.
Question 12.

Answer: 15
Explanation:
Any number divided by 1 will be the same number.
15/1 = 1
Thus the quotient is 15.
Question 13.
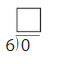
Answer: 0
Explanation:
Any number divided by 0 will be always 0.
0/6 = 0
Thus the quotient is 0.
Question 14.

Answer: 1
Explanation:
24/24 = 1
Thus the quotient is 1.
Find the missing dividend or divisor.
Question 15.
2 ÷ ____ = 2
Answer: 1
Explanation:
Let the missing divisor be x.
2 ÷ x = 2
2/x = 2
2 = 2 × x
x = 2/2
x = 1
Thus the missing divisor is 1.
Question 16.
____ ÷ 12 = 0
Answer: 0
Explanation:
Let the missing divisor be y.
y ÷ 12 = 0
y/12 = 0
y = 0 × 12
y = 0
Thus the missing divisor is 0.
Question 17.
8 ÷ ____ = 1
Answer: 8
Explanation:
Let the missing divisor be z.
8 ÷ z = 1
8/z = 1
8 = 1 × z
z = 8
Thus the missing divisor is 8.
Compare
Question 18.
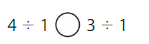
Answer: >
Explanation:
Divide the two numbers
4 ÷ 1 = 4
3 ÷ 1 = 3
4 > 3
So, 4 ÷ 1 > 3 ÷ 1
Question 19.

Answer: =
Explanation:
Any number divided by 0 will be always 0.
0 ÷ 6 = 0
0 ÷ 9 = 0
So, 0 ÷ 6 = 0 ÷ 9
Question 20.

Answer: <
Explanation:
Any number divided by 0 will be always 0.
0 ÷ 5 = 0
7 ÷ 1 = 7
0 < 7
0 ÷ 5 < 7 ÷ 1
Question 21.
There are 2 cheese blocks. Each mousetrap has 1 cheese block on it. How many mousetraps are there?

Answer: 2
Explanation:
Given that,
There are 2 cheese blocks. Each mousetrap has 1 cheese block on it.
2 ÷ 1 = 2
Thus there are 2 mousetraps.
Question 22.
Reasoning
Your friend says 14 ÷ 0 and 0 ÷ 14 both equal 0. Is your friend correct? Explain.
Answer: Incorrect
Explanation:
Your friend is incorrect because 0 divided by any number except 0 will be always 0.
0/14 = 0
but
14/0 = infinity
Think and Grow: Modeling Real Life
A clown shares 10 balloons equally with 10 children. How many balloons does each child receive?

Division equation:
Each child receives a _____ balloon.
Answer: 1
Explanation:
Given that,
A clown shares 10 balloons equally with 10 children.
10/10 = 1
Therefore each child receives 1 balloon.
Show and Grow
Question 23.
You have 9 tokens. You need 1 token to play an arcade game. How many games can you play?
Answer: 9
Explanation:
Given that,
You have 9 tokens. You need 1 token to play an arcade game.
9/1 = 9
Thus you can play 9 games.
Question 24.
You have 9 quarters. You put 5 of them in your backpack. You divide the other quarters equally among 4 friends. How many quarters does each friend get?
Answer: 1
Explanation:
Given,
You have 9 quarters. You put 5 of them in your backpack.
9 – 5 = 4
You divide the other quarters equally among 4 friends.
4/4 = 1
Thus each friend gets 1 quarter.
Question 25.
You ask your friend the question below.
“What is 475 divided by475?”
Your friend immediately says 1. How does your friend solve the problem so quickly? Explain.
Answer:
475/475 = 1
Your friend solved the problem very quickly because he used the logic ” Any number divided by the same number will be always 1″.
Divide by 0 or 1 Homework & Practice 4.7
Write the related multiplication fact. Then find the quotient.
Question 1.
3 ÷ 1 = _____
Answer: 3
Explanation:
The related multiplication fact for 1,3
1 × 3 = 3
3 × 1 = 3
Divide the two numbers
3 ÷ 1 = 3
Thus the quotient is
Question 2.
0 ÷ 7 = _____
Answer: 0
Explanation:
The related multiplication fact for 0, 7
0 × 7 = 0
7 × 0 = 0
Divide the two numbers 0, 7
0/7 = 0
Thus the quotient is 0
Find the quotient.
Question 3.
8 ÷ 1 = _____
Answer: 8
Explanation:
The related multiplication fact for 1, 8
8 × 1 = 8
1 × 8 = 8
Divide the two numbers 8, 1
8/1 = 8
Thus the quotient is 8
Question 4.
0 ÷ 2 = _____
Answer: 0
Explanation:
The related multiplication fact for 0, 2
0 × 2 = 0
2 × 0 = 0
Divide the two numbers
0/2 = 0
Thus the quotient is 0
Question 5.
7 ÷ 7 = _____
Answer: 1
Explanation:
The related multiplication fact for 7, 1
1 × 7 = 7
7 × 1 = 7
Divide the two numbers
7/7 = 1
Thus the quotient is 1
Question 6.

Answer: 1
Explanation:
The related multiplication fact for 1, 12
12 × 1 = 12
1 × 12 = 12
Divide the two numbers
12/12 = 1
Thus the quotient is 1
Question 7.
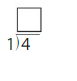
Answer: 4
Explanation:
The related multiplication fact for 1, 4
1 × 4 = 4
4 × 1 = 4
Divide the two numbers
4/1 = 4
Thus the quotient is 4
Question 8.
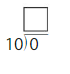
Answer: 0
Explanation:
The related multiplication fact for 0, 10
0 × 10 = 0
10 × 0 = 0
Divide the two numbers
0/10 = 0
Thus the quotient is 0
Find the missing dividend or divisor
Question 9.
____ ÷ 3 = 0
Answer: 0
Explanation:
Let the missing dividend be x
x ÷ 3 = 0
x/3 = 0
x = 0 × 3
x = 0
Thus the missing dividend is 0.
Question 10.
10 ÷ ____ = 10
Answer: 1
Explanation:
Let the missing divisor be y.
10 ÷ y = 10
10/y = 10
10 = y × 10
y = 10/10
y = 1
Thus the missing divisor is 1.
Question 11.
____ ÷ 4 = 0
Answer: 0
Explanation:
Let the missing dividend be z.
z ÷ 4 = 0
z/4 = 0
z = 0 × 4
z = 0
Thus the missing dividend is 0.
Compare
Question 12.
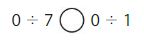
Answer: =
Explanation:
Divide the two numbers
0 ÷ 7 = 0
0 ÷ 1 = 0
0 = 0
0 ÷ 7 = 0 ÷ 1
Question 13.
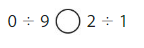
Answer: <
Explanation:
Divide the two numbers
0 ÷ 9 = 0
2 ÷ 1 = 2
0 < 2
0 ÷ 9 < 2 ÷ 1
Question 14.
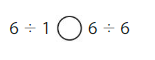
Answer: >
Explanation:
Divide the two numbers
6 ÷ 1 = 6
6 ÷ 6 = 1
6 > 1
6 ÷ 1 > 6 ÷ 6
Question 15.
Reasoning
How are the multiplication rules for 0 and 1 similar to the division rules for 0 and 1? How are they different?
Answer:
Multiplication and division are closely related, given that division is the inverse operation of multiplication. When we divide, we look to separate into equal groups, while multiplication involves joining equal groups.
multiplication rules for 0 and 1 are not similar to division rules for 0 and 1.
Any number multiplied by 0 will be zero.
But any number divided by 0 will be infinity.
Question 16.
Number Sense
Which has the greatest quotient?
6 ÷ 6
4 ÷ 1
0 ÷ 8
3 ÷ 1
Answer: 4 ÷ 1
Explanation:
6 ÷ 6 = 1
4 ÷ 1 = 4
0 ÷ 8 = 0
3 ÷ 1 = 3
Thus the correct answer is option b.
Question 17.
DIG DEEPER!
Use the numbers 0, 1, 5, and 10 to make the number sentence true.
____ ÷ _____ < _____ ÷ ______
Answer:
You need to write the equation by using the above numbers.
0 ÷ 1 < 5 ÷ 10
Question 18.
Modeling Real Life
There are 5 bird eggs. An equal number of eggs hatch each day for 5 days. How many eggs hatch each day?

Answer:
Given that,
There are 5 bird eggs. An equal number of eggs hatch each day for 5 days.
5/5 = 1
Therefore 1 egg hatch each day.
Question 19.
Modeling Real Life
A hotel orders twenty-four 48-inch televisions and twenty-six 60-inch televisions. The hotel puts 1 television in each room. How many rooms can get a new television?
Answer:
Given,
A hotel orders twenty-four 48-inch televisions and twenty-six 60-inch televisions.
The hotel puts 1 television in each room.
24 + 26 = 50
Thus 50 rooms can get a new television.
Review & Refresh
Find the product.
Question 20.
2 × 4 × 1 = _____
Answer: 8
Explanation:
First multiply 2 × 4
2 × 4 = 8
8 × 1 = 8
So, 2 × 4 × 1 = 8
Question 21.
2 × 3 × 5 = _____
Answer: 30
Explanation:
Multiply 2 and 3
2 × 3 = 6
6 × 5 = 30
So, 2 × 3 × 5 = 30
Question 22.
2 × 3 × 7 = _____
Answer: 42
Explanation:
Multiply 2 and 3
2 × 3 = 6
6 × 7 = 42
So, 2 × 3 × 7 = 42
Question 23.
5 × (2 × 9) = _____
Answer: 90
Explanation:
First, multiply the numbers in the bracket.
2 × 9 = 18
18 × 5 = 90
Question 24.
2 × (3 × 3) = _____
Answer: 18
Explanation:
First, multiply the numbers in the bracket.
3 × 3 = 9
9 × 2 = 18
Question 25.
2 × (8 × 1) = _____
Answer: 16
Explanation:
First, multiply the numbers in the bracket.
8 × 1 = 8
2 × 8 = 16
Lesson 4.8 Practice Division Strategies
Explore and Grow
Use and Strategies to find the quotient
36 ÷ 4 = _____
Answer: 9
Explanation:
You can find the quotient by using the number line.
Construct Arguments
What other strategies can you use to solve? Explain the strategy to your partner.
Answer:
You can also find the quotient by using the repeated subtraction.
36 – 4 = 32
32 – 4 = 28
28 – 4 = 24
24 – 4 = 20
20 – 4 = 16
16 – 4 = 12
12 – 4 = 8
8 – 4 = 4
4 – 4 = 0
Count the number of times subtraction repeated.
The subtraction repeated 9 times.
Thus the quotient is 9.
Think and Grow: Practice Division Strategies
Example
Find 45 ÷ 5.
One Way:
Use a multiplication fact. Draw an array to help.
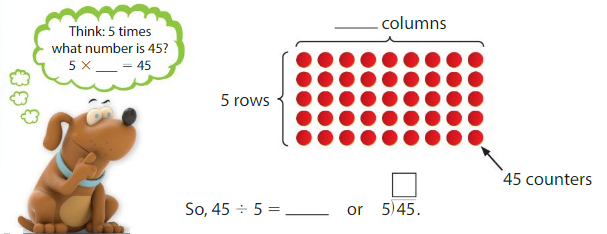
Another Way:
Use a number line. Start at 45. Count back by 5s until you reach 0.
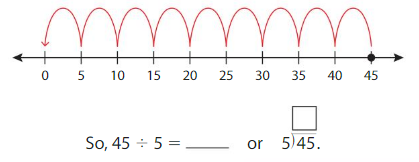
Show and Grow
Use any strategy to find the quotient.
Question 1.
30 ÷ 6 = _____
Answer: 5
Explanation:

Multiplication:
5 rows of 6 counters
5 × 6 = 30
30 counters
Division:
30 counters in 5 equal rows
30 ÷ 5 = 6
60 counters in each row.
Fact family for 5, 6 and 30:
5 × 6 = 30
6 × 5 = 30
30 ÷ 5 = 6
30 ÷ 6 = 5
Question 2.
56 ÷ 8 = _____
Answer: 7
Explanation:
Number of rows = 8
Number of counters = 56
Divide the number of rows by the number of counters.
56/8 = 7
Thus the quotient is 7.
Apply and Grow: Practice
Use any strategy to find the quotient.
Question 3.
40 ÷ 10 = _____
Answer: 4
Explanation:
You can find the quotient by using the repeated subtraction.
40 – 10 = 30
30 – 10 = 20
20 – 10 = 10
10 – 10 = 0
Thus the quotient is 4.
Question 4.
18 ÷ 3 = _____
Answer: 6
Explanation:
You can find the quotient by using the repeated subtraction.
18 – 3 = 15
15 – 3 = 12
12 – 3 = 9
9 – 3 = 6
6 – 3 = 3
3 – 3 = 0
Thus the quotient is 6.
Question 5.
49 ÷ 7 = ____
Answer: 7
Explanation:
You can find the quotient by using the repeated subtraction.
49 – 7 = 42
42 – 7 = 35
35 – 7 = 28
28 – 7 = 21
21 – 7 = 14
14 – 7 = 7
7 – 7 = 0
Thus the quotient is 7.
Question 6.
____ = 36 ÷ 9
Answer: 4
Explanation:
You can find the quotient by using the repeated subtraction.
36 – 9 = 27
27 – 9 = 18
18 – 9 = 9
9 – 9 = 0
Thus the quotient is 4.
Question 7.
____ = 4 ÷ 4
Answer: 1
Explanation:
You can find the quotient by using the repeated subtraction.
4 – 4 = 0
Thus the quotient is 1.
Question 8.
______ = 18 ÷ 2
Answer: 9
Explanation:
You can find the quotient by using the repeated subtraction.
18 – 2 = 16
16 – 2 = 14
14 – 2 = 12
12 – 2 = 10
10 – 2 = 8
8 – 2 = 6
6 – 2 = 4
4 – 2 = 2
2 – 2 = 0
Thus the quotient is 0.
Question 9.
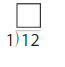
Answer: 12
Explanation:
You can find the quotient by using the repeated subtraction.
12 – 1 = 11
11 – 1 = 10
10 – 1 = 9
9 – 1 = 8
8 – 1 = 7
7 – 1 = 6
6 – 1 = 5
5 – 1 = 4
4 – 1 = 3
3 – 1 = 2
2 – 1 = 1
1 – 1 = 0
Thus the quotient is 12.
Question 10.

Answer: 8
Explanation:
Divide the two numbers 5 and 40
40/5 = 8
Thus the quotient is 8.
Question 11.

Answer: 6
Explanation:
Divide the two numbers 8 and 48
48/8 = 6
Thus the quotient is 6.
Question 12.

Answer: 4
Explanation:
Divide the two numbers 6 and 24
24/6 = 4
Thus the quotient is 4.
Question 13.
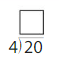
Answer: 5
Explanation:
Divide the two numbers 4 and 20.
20/4 = 5
Thus the quotient is 5.
Question 14.

Answer: 3
Explanation:
Divide the two numbers 7 and 21
21/7 = 3
Thus the quotient is 3.
Question 15.
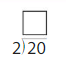
Answer: 10
Explanation:
Divide the two numbers 2 and 20.
20/2 = 10
Thus the quotient is 10.
Question 16.
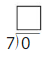
Answer: 0
Explanation:
Divide the two numbers 0 and 7
0/7 = 0
Thus the quotient is 0.
Question 17.
Divide 54 by 6.
Answer: 9
Explanation:
Divide the two numbers 54 and 6.
54/6 = 9
Thus the quotient is 9.
Question 18.
Divide 27 by 9.
Answer: 3
Explanation:
Divide the two numbers 9 and 27.
27/9 = 3
Thus the quotient is 3.
Question 19.
Divide 70 by 10.
Answer: 7
Explanation:
Divide the two numbers 10 and 70
70/10 = 7
Thus the quotient is 7.
Question 20.
A construction worker wants to build a 32-foot-long wall in 8 hours. How many feet should he complete each hour so that it is built on time?

Answer: 4
Explanation:
Given that,
A construction worker wants to build a 32-foot-long wall in 8 hours.
32/4 = 4
Thus he should complete 4 feet each hour.
Question 21.
Writing
How can you use multiplication to help find 42 ÷ 7? Explain.
Answer:
42 = x × 7
x = 42/7
x = 6
So, 42 ÷ 7 = 6
Question 22.
YOU BE THE TEACHER
Your friend says she only needs to write two equations for the 4, 4, 16 fact family. Is your friend correct? Explain.
Answer:
4 × 4 = 16
16 ÷ 4 = 4
Yes, your friend is correct.
Think and Grow: Modeling Real Life
There are 72 oranges at a grocery store arranged into an array with 9 columns. There are 80 lemons arranged into an array with 8 columns. Which fruits as more rows?

Models:
Division equations:
The ______ have more rows.
Answer:
Given that,
There are 72 oranges at a grocery store arranged into an array with 9 columns.
72 ÷ 9 = 8
There are 80 lemons arranged into an array with 8 columns.
80 ÷ 8 = 10
Thus lemons have more rows.
Show and Grow
Question 23.
There are 63 peaches arranged into an array with 7 rows. There are 70 pears arranged into an array with 10 rows. Which fruit has more columns?

Answer:
Given,
There are 63 peaches arranged into an array with 7 rows.
63 ÷ 7 = 9
There are 70 pears arranged into an array with 10 rows.
70 ÷ 10 = 7
Thus peaches have more columns.
Question 24.
Newton has 20 quarters. He wants to trade all of them for bills. How many $1 bills would he get? How many $5 bills would he get?
Answer:
Given that,
Newton has 20 quarters. He wants to trade all of them for bills
20/5 = 4
Thus he will get four $5 bills.
Question 25.
A box of fruit snacks costs $5. Each box has 8 bags. Descartes spends $20 on fruit snacks. How many bags of fruit snacks does he get?
Answer:
Given that,
A box of fruit snacks costs $5. Each box has 8 bags.
$5 × 8 = $40
Descartes spends $20 on fruit snacks.
40 – 20 = $20
Thus Descartes get 4 bags of fruit snacks.
Practice Division Strategies Homework & Practice 4.8
Use any strategy to find the quotient
Question 1.
8 ÷ 1 = ____
Answer: 8
Explanation:
Divide the two numbers 8 and 1.
8/1 = 8
Thus the quotient is 8.
Question 2.
25 ÷ 5 = _____
Answer: 5
Explanation:
Divide the two numbers 5 and 25.
25/5 = 5
Thus the quotient is 5.
Question 3.
72 ÷ 8 = _____
Answer: 9
Explanation:
Divide the two numbers 8 and 72.
72/8 = 9
Thus the quotient is 9.
Question 4.
____ = 45 ÷ 9
Answer: 5
Explanation:
Divide the two numbers 9 and 45
45/9 = 5
Thus the quotient is 5.
Question 5.
____ = 0 ÷ 3.
Answer: 0
Explanation:
Divide the two numbers 0 and 3.
0 divided by any number is zero.
0/3 = 0
Thus the quotient is 0.
Question 6.
____ = 18 ÷ 2
Answer: 9
Explanation:
Divide the two numbers 18 and 2.
18/2 = 9
Thus the quotient is 9.
Question 7.
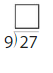
Answer: 3
Explanation:
Divide the two numbers 9 and 27.
27/9 = 3
Thus the quotient is 3.
Question 8.
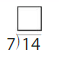
Answer: 2
Explanation:
Divide the two numbers 14 and 7.
14/7 = 2
Thus the quotient is 2.
Question 9.

Answer: 10
Explanation:
Divide the two numbers 2 and 20.
20/2 = 10
Thus the quotient is 10.
Question 10.

Answer: 4
Explanation:
Divide the two numbers 3 and 12
12/3 = 4
Thus the quotient is 4.
Question 11.
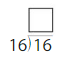
Answer: 1
Explanation:
Divide the two numbers 16 and 16
16/16 = 1
Thus the quotient is 1.
Question 12.
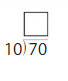
Answer: 7
Explanation:
Divide the two numbers 10 and 70.
70/10 = 7
Thus the quotient is 7.
Question 13.

Answer: 6
Explanation:
Divide the two numbers 5 and 30.
30/5 = 6
Thus the quotient is 6.
Question 14.
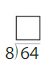
Answer: 8
Explanation:
Divide the two numbers 8 and 64.
64/8 = 8
Thus the quotient is 8.
Question 15.
Divide 60 by 6.
Answer: 10
Explanation:
Divide the two numbers 6 and 60
60/6 = 10
Thus the quotient is 10.
Question 16.
Divide 9 by 3.
Answer: 3
Explanation:
Divide the two numbers 3 and 9.
9/3 = 3
Thus the quotient is 3.
Question 17.
Divide 63 by 9.
Answer: 7
Explanation:
Divide the two numbers 9 and 63.
63/9 = 7
Thus the quotient is 7.
Question 18.
DIG DEEPER!
Without dividing, how can you tell which quotient is smaller, 30 ÷ 5 or 30 ÷ 6? Explain.
Answer: The quotient of 30 ÷ 6 is smaller.
Explanation:
The largest divisor will have the smallest quotient.
30 ÷ 5 = 6
30 ÷ 6 = 5
Question 19.
Number Sense
Which expressions have a quotient of 7?

Answer:

Explanation:
70/10 = 7
64/8 = 8
35 ÷ 5 = 7
42 ÷ 7 = 6
21 ÷ 3 = 7
24 ÷ 8 = 3
7 ÷ 1 = 7
Question 20.
Reasoning
Use +, -, ×, or to complete the equations.
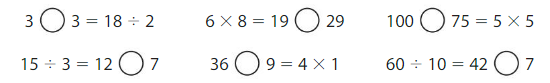
Answer:
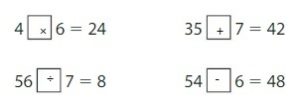
Question 21.
Modeling Real Life
Newton has 60 dimes. He trades all of them for $1 bills. How many bills does he get?

Answer: 6
Explanation:
Newton has 60 dimes. He trades all of them for $1 bills.
Convert from dime to dollar.
10 dime = 1 dollar
60 dimes = $6
Question 22.
Modeling Real Life
Two girls are getting braids in their hair. The first girl wants a total of 30 beads with 3 beads on each braid. The second girl wants a total of 45 beads with 5 beads on each braid. Which girl has more braids?
Answer:
Given that,
Two girls are getting braids in their hair.
The first girl wants a total of 30 beads with 3 beads on each braid.
30/3 = 10
The second girl wants a total of 45 beads with 5 beads on each braid.
45/5 = 9
The first girl has more braids.
Review & Refresh
Find the sum.
Question 23.

Answer: 597
460
+137
597
Question 24.

Answer: 932
625
+297
932
Question 25.
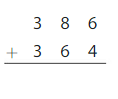
Answer: 750
386
+ 364
750
Lesson 4.9 Problem Solving: Division
Explore and Grow
Use any strategy to solve.
There are 27 cups for a cup-stacking game. There are 3 players. Each player gets an equal number of cups. How many cups does each player get?

Answer:
Given,
There are 27 cups for a cup-stacking game.
There are 3 players.
27/3 = 9
Each player gets an equal number of cups.
Thus each player gets 9 cups.
Reasoning
Compare your strategy to your partner’s strategy. How are they the same? How are they different?
Think and Grow: Using the Problem-Solving Plan
Example
Newton buys a box of flower vases. The box has 2 rows with 4 vases in each row. The box costs $48. How much does each vase cost?
Understand the Problem
What do you need to find?
• You need to find how much each ______ costs.
Answer: You need to find each vase cost.
What do you know?
• The box has ______ rows of vases.
• Each row has ______ vases.
• The box costs _____.
Answer:
• The box has 2 rows of vases.
• Each row has 4 vases.
• The box costs $48.
Make a Plan
How will you solve?
• Multiply _____ by ______ to find how many _______ are in the box.
• Then divide _______ by the product.
Answer:
• Multiply 2 by 4 to find how many vases are in the box.
• Then divide cost by the product.
Solve
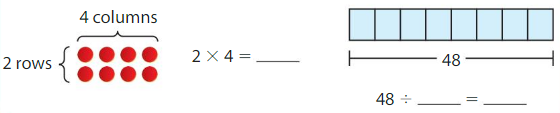
Each vase costs _______.
Answer:
2 × 4 = 8
48/8 = 6
Thus each vase cost $6.
Show and Grow
Question 1.
Descartes buys 3 packs of colored pencils and a backpack. He spends $33. The backpack costs $12. Each pack of colored pencils costs the same amount. How much is each pack of colored pencils?
Answer:
Given,
Descartes buys 3 packs of colored pencils and a backpack.
He spends $33. The backpack costs $12.
33 – 12 = $21
Each pack of colored pencils costs the same amount.
21/3 = $7
Thus each pack of colored pencils is $7.
Apply and Grow: Practice
Question 2.
You have 4 pages of homework and 2 chores to complete before you get free time. Each task takes 7 minutes to complete. You have60 minutes until dinner. What information do you know that will help you find how much free time you will have before dinner?
Answer:
Given that,
You have 4 pages of homework and 2 chores to complete before you get free time.
Each task takes 7 minutes to complete.
4 + 2 = 6
6 × 7 = 42 minutes
You have 60 minutes until dinner.
60 – 42 = 18 minutes
You will have 18 minutes of free time before dinner.
Question 3.
You are using dots to create a picture. You use 99 dots in all. Forty-six are blue. Thirty-five are purple. You use an equal number of yellow and green dots for the rest of the picture. How many green dots are in your picture?

Answer:
Given,
You are using dots to create a picture. You use 99 dots in all. Forty-six are blue.
Thirty-five are purple.
35 + 46 = 81
99 – 81 = 18
You use an equal number of yellow and green dots for the rest of the picture.
18/2 = 9
You use 9 yellow dots and 9 green dots.
Question 4.
You are making oatmeal for each of your 4 family members. You have 36 raisins and 20 blueberries. You want everyone to get an equal number of each. How many raisins and how many blueberries should you put in each bowl?


Answer:
Given that,
You are making oatmeal for each of your 4 family members.
You have 36 raisins and 20 blueberries.
36 + 20 = 56
You want everyone to get an equal number of each.
56/4 = 14
Therefore 14 raisins and blueberries should put in each bowl.
Think and Grow: Modeling Real Life
You have 2 boxes of crayons. One box has 24 crayons. The other box has 48 crayons. Eighteen of the crayons are broken. You put the crayons that are not broken, into 6 equal groups. How many crayons are in each group?

Understand the problem:
Make a plan:
Solve:
There are _____ crayons in each group.
Answer:
You have 2 boxes of crayons. One box has 24 crayons. The other box has 48 crayons.
24 + 48 = 72 crayons
Eighteen of the crayons are broken.
72 – 18 = 54 crayons
You put the crayons that are not broken, into 6 equal groups.
54/6 = 9 crayons.
Therefore there are 9 crayons in each group.
Show and Grow
Question 5.
You have 2 bags of beach glass. One bag has 17 pieces. The other bag has 18 pieces. You give 5 pieces to your friend. You sort the rest of the pieces into 3 equal groups. How many pieces are in each group?

Explain how you can check your answer.
Answer:
Given,
You have 2 bags of beach glass. One bag has 17 pieces. The other bag has 18 pieces.
17 + 18 = 35 pieces
You give 5 pieces to your friend.
35 – 5 = 30 pieces
You sort the rest of the pieces into 3 equal groups.
30/3 = 10
Thus there are 10 pieces in each group.
Problem Solving: Division Homework & Practice 4.9
Question 1.
A truck carries 4 chairs and a table. The table weighs 35 pounds. The total weight of the chairs and table is 63 pounds. How much does each chair weigh?
Answer: 7 pounds
Explanation:
Given that,
A truck carries 4 chairs and a table. The table weighs 35 pounds.
The total weight of the chairs and table is 63 pounds.
63 pounds – 35 pounds = 28 pounds
There are 4 chairs.
Divide 28 by 4 to find the weight of each chair.
28/4 = 7
Therefore each chair weighs 7 pounds.
Question 2.
You volunteer at a nursing home for 3 hours a day. You volunteered 6 hours last week and 12 hours this week. How many days did you volunteer?
Answer: 6 days
Explanation:
Given that,
You volunteer at a nursing home for 3 hours a day.
You volunteered 6 hours last week and 12 hours this week.
6 hours – 2 days
12 hours – 4 days
4 + 2 = 6 days
Thus you volunteer for 6 days.
Question 3.
Writing Write and solve your own word problem involving division.
Answer:
You work for 49 hours a week. How many hours do you work in a day?
Explanation:
You work for 49 hours a week.
Convert from weeks to days
1 week = 7 days
49/7 = 7 hours
Thus you work 7 hours a day.
Question 4.
Modeling Real Life
You have 2 trays of flavored ice cubes. One tray has 16 ice cubes. The other tray has 12 ice cubes. Eight of the ice cubes are not completely frozen yet. You divide the frozen ice cubes equally into 5 glasses. How many ice cubes are in each glass?
Answer:
Given that,
You have 2 trays of flavored ice cubes. One tray has 16 ice cubes.
16 × 2 = 32 ice cubes
The other tray has 12 ice cubes. Eight of the ice cubes are not completely frozen yet.
12 – 8 = 4
32 + 4 = 36 ice cubes
You divide the frozen ice cubes equally into 5 glasses.
36/5 = 7(approx)
Thus you divide 7 frozen ice cubes equally into 5 glasses.
Question 5.
Modeling Real Life
You have 2 bags of seashells. One bag has 13 seashells. The other bag has 25 seashells. You give6 seashells to your friend. You sort the rest of the seashells into 4 equal groups. How many seashells are in each group?

Answer:
Given that,
You have 2 bags of seashells. One bag has 13 seashells.
2 × 13 = 26 seashells
The other bag has 25 seashells. You give 6 seashells to your friend.
25 – 6 = 19
You sort the rest of the seashells into 4 equal groups.
26 + 19 = 45 seashells
45/4 = 11 (approx)
Thus there are 11 seashells in 4 equal groups.
Review & Refresh
Question 6.
Answer:
i. 5 sides
ii. 5 vertices
iii. pentagon
Explanation:
The above figure consists of 5 sides and 5 vertices. The polygon with 5 sides is called a pentagon.
Question 7.
Answer:
i. 4 sides
ii. 4 vertices
iii. Quadrilateral
Explanation:
The above figure consists of 4 sides and 4 vertices. The polygon with 4 sides is called a Quadrilateral.
Division Facts and Strategies Performance Task
You, your friend, and your cousin run for class president. Three teachers and 60 students are gathered in the gym for the election.
Question 1.
There is one teacher in each row. Each row has the same number of students. Find the number of people sitting in each row.

Answer:
Given that,
You, your friend, and your cousin run for class president.
Three teachers and 60 students are gathered in the gym for the election.
There is one teacher in each row. Each row has the same number of students.
60/3 = 20 students
Thus 20 people are sitting in each row.
Question 2.
Sixty students vote in the election. Thirty students vote for you. Twenty students vote for your friend. Five students vote for your cousin.
a.How many students still need to vote?
Answer:
Sixty students vote in the election. Thirty students vote for you.
60 – 30 = 30
Twenty students vote for your friend.
30 – 20 = 10
Five students vote for your cousin.
10 – 5 = 5
Thus still 5 students need to vote.
b.The remaining students all vote for your cousin. Complete the picture graph.

Answer:

Question 3.
As class president, you raise $95 to buy new toys for the school playground. Each ball costs $8 and each flying disc costs $6. You want to buy some balls and 3 flying discs. How many balls can you buy? How much money do you have left?
Answer:
Given that,
As class president, you raise $95 to buy new toys for the school playground.
Each ball costs $8 and each flying disc costs $6.
You want to buy some balls and 3 flying discs.
3 × $6 = $18
$95 – $18 = $77
We need to how many balls can you buy for $77.
72/8 = 9
77 – 72 = 5
Thus $5 left.
Division Facts and Strategies Activity
Four in a Row Blastoff!
Directions:
1. Players take turns rolling the die.
2. On your turn, choose and solve any division expression in the row of your roll. If you find the correct answer, place a counter on the space.
3. The first player to create 4 counters in a row, horizontally, vertically, or diagonally, wins! A spaceship blasts off! Cross out one spaceship and play again until all spaceships have blasted off!
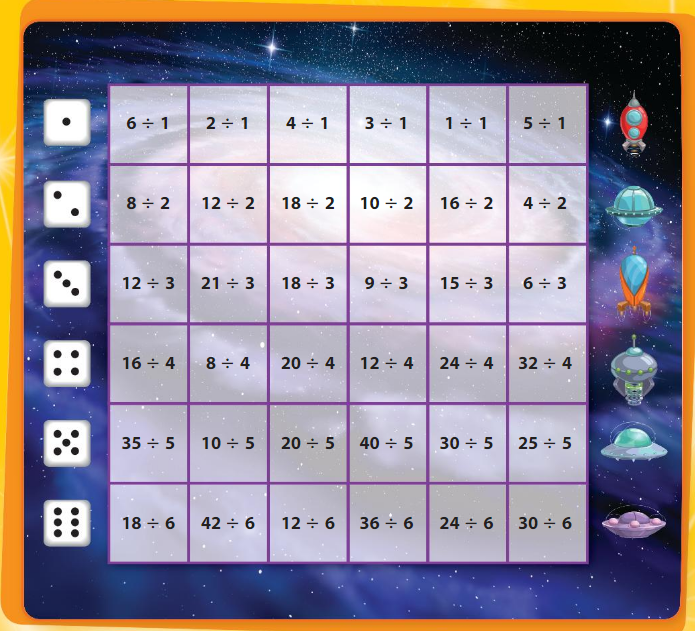
Answer:
I choose 3, 9 ÷ 3 = 3
I choose 4, 16 ÷ 4 = 4
I choose 5, 25 ÷ 5 = 5
I choose 6, 36 ÷ 6 = 6
Division Facts and Strategies Chapter Practice
4.1 Use Arrays to Divide
Question 1.
There are 20 counters. The counters are in 4 equal rows. How many counters are in each row?
4 rows of ____
20 ÷ 4 = _____
Answer:
Given that,
There are 20 counters. The counters are in 4 equal rows.
20/4 = 5
Thus there are 4 rows of 5 counters
20 ÷ 4 = 5
Thus there are 5 counters in each row.
Question 2.
You have 32 counters. You arrange them with 8 counters in each row. How many rows of counters do you make?
____ rows of 8
32 ÷ 8 = _____
Answer:
Given,
You have 32 counters. You arrange them with 8 counters in each row.
32/8 = 4
4 rows of 8.
32 ÷ 8 = 4
Thus there are 4 rows of counters.
Question 3.
Precision
Label the parts of the division problem using quotient, dividend, and divisor
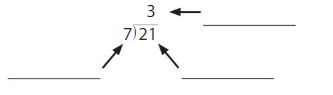
Answer:
The label for the above problem is
21 is dividend
3 is quotient
7 is divisor
4.2 Relate Multiplication and Division
Write the fact family for the numbers.
Question 4.
1, 5, 5
Answer:
The fact family for the numbers is
Multiplication Equation:
1 × 5 = 5
5 × 1 = 5
Division Equation:
5 ÷ 5 = 1
5 ÷ 1 = 5
Question 5.
2, 7, 14
Answer:
The fact family for the numbers is
Multiplication Equation:
2 × 7 = 14
7 × 2 = 14
Division Equation:
14 ÷ 2 = 7
14 ÷ 7 = 2
Question 6.
9, 5, 45
Answer:
The fact family for the numbers is
Multiplication Equation:
9 × 5 = 45
5 × 9 = 45
Division Equation:
45 ÷ 5 = 9
45 ÷ 9 = 5
Question 7.
8, 6, 48
Answer:
The fact family for the numbers is
Multiplication Equation:
8 × 6 = 48
6 × 8 = 48
Division Equation:
48 ÷ 6 = 8
48 ÷ 8 = 6
4.3 Divide 2, 5, or 10
Write the related multiplication fact. The find the quotient.
Question 8.
Find 15 ÷ 5
5 × ____ = 15
15 ÷ 5 = ____
Answer:
Let the unknown number be x.
5 × x = 15
x = 15/5
x = 3
15 ÷ 5 = 3
Question 9.
Find 14 ÷ 2
2 × ____ = 14
14 ÷ 2 = ____
Answer:
Let the unknown number be x.
2 × x = 14
x = 14/2
x = 7
14 ÷ 2 = 7
Question 10.
Find 40 ÷ 10
10 × ____ = 40
40 ÷ 10 = ____
Answer:
Let the unknown number be x.
10 × x = 40
x = 40/10
x = 4
40 ÷ 10 = 4
Find the quotient.
Question 11.
60 ÷ 10 = _____
Answer: 6
Explanation:
Divide the two numbers 60 and 10.
60/10 = 6
Thus the quotient is 6.
Question 12.
20 ÷ 5 = _____
Answer: 4
Explanation:
Divide the two numbers 20 and 5.
20/5 = 4
Thus the quotient is 4.
Question 13.
20 ÷ 2 = _____
Answer: 10
Explanation:
Divide the two numbers 20 and 2.
20/2 = 10
Thus the quotient is 10.
Question 14.
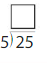
Answer: 5
Explanation:
Divide the two numbers 25 and 5.
25/5 = 5
Thus the quotient is 5.
Question 15.

Answer: 9
Explanation:
Divide the two numbers 18 and 2.
18/2 = 9
Thus the quotient is 9.
Question 16.
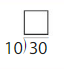
Answer: 3
Explanation:
Divide the two numbers 30 and 10.
30/10 = 3
Thus the quotient is 3.
4.4 Divide by 3 or 4
Find the quotient.
Question 17.
18 ÷ 3 = _____
Answer: 6
Explanation:
Divide the two numbers 18 and 3.
18/3 = 6
Thus the quotient is 6.
Question 18.
40 ÷ 4 = ____
Answer: 10
Explanation:
Divide the two numbers 40 and 4.
40/4 = 10
Thus the quotient is 10.
Question 19.
24 ÷ 4 = _____
Answer: 6
Explanation:
Divide the two numbers 24 and 4.
24/4 = 6
Thus the quotient is 6.
Question 20.

Answer: 9
Explanation:
Divide the two numbers 3 and 27.
27/3 = 9
Thus the quotient is 9.
Question 21.

Answer: 3
Explanation:
Divide the two numbers 12 and 4.
12/4 = 3
Thus the quotient is 3.
Question 22.

Answer: 8
Explanation:
Divide the two numbers 24 and 3.
24/3 = 8
Thus the quotient is 8.
Question 23.
Structure
Write the division equation represented by the number line.
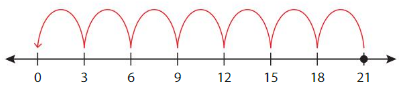
____ ÷ ____ = ____
Answer: 21 ÷ 3 = 7
Explanation:
The count starts from 0.
The count jumps for every 3s.
The division equation is 21 ÷ 3 = 7
4.5 Divide by 6 or 7
Find the quotient
Question 24.
42 ÷ 6 = _____
Answer: 7
Explanation:
Divide the two numbers 42 and 6.
42/6 = 7
Thus the quotient is 7.
Question 25.
54 ÷ 6 = _____
Answer: 9
Explanation:
Divide the two numbers 54 and 6.
54/6 = 9
Thus the quotient is 9.
Question 26.
28 ÷ 7 = ____
Answer: 4
Explanation:
Divide the two numbers 28 and 7.
28/7 = 4
Thus the quotient is 4.
Question 27.
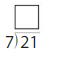
Answer: 3
Explanation:
Divide the two numbers 21 and 7.
21/7 = 3
Thus the quotient is 3.
Question 28.

Answer: 6
Explanation:
Divide the two numbers 7 and 42.
42/7 = 6
Thus the quotient is 6.
Question 29
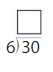
Answer: 5
Explanation:
Divide the two numbers 30 and 6.
30/6 = 5
Thus the quotient is 5.
Find the missing divisor
Question 30.
18 ÷ ____ = 6
Answer: 3
Explanation:
Let the missing divisor be u.
18 ÷ u = 6
18/u = 6
18 = 6 × u
u = 18/6
u = 3
Thus the missing divisor is 3.
Question 31.
35 ÷ ____ = 7
Answer: 5
Explanation:
Let the missing divisor be v.
35 ÷ v = 7
35/v = 7
35 = 7 × v
v = 35/7
v = 5
Thus the missing divisor is 5.
Question 32.
36 ÷ ____ = 6
Answer: 6
Explanation:
Let the missing divisor be w.
36 ÷ w = 6
36/w = 6
36 = 6 × w
w = 36/6
w = 6
Thus the missing divisor is 6.
4.6 Divide by 8 or 9
Find the quotient
Question 33.
36 ÷ 9 = _____
Answer: 4
Explanation:
Divide the two numbers 36 and 9
36/9 = 4
Thus the quotient is 4.
Question 34.
64 ÷ 8 = ____
Answer: 8
Explanation:
Divide the two numbers 8 and 64
64/8 = 8
Thus the quotient is 8.
Question 35.
90 ÷ 9 = _____
Answer: 10
Explanation:
Divide the two numbers 90 and 9.
90/9 = 10
Thus the quotient is 10.
Question 36.

Answer: 4
Explanation:
Divide the two numbers 32 and 8.
32/8 = 4
Thus the quotient is 4.
Question 37.

Answer: 5
Explanation:
Divide the two numbers 45 and 9.
45/9 = 5
Thus the quotient is 5.
Question 38.
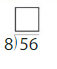
Answer: 7
Explanation:
Divide the two numbers 56 and 8
56/8 = 7
Thus the quotient is 7.
Compare
Question 39.

Answer: >
Explanation:
Divide the two numbers.
63 ÷ 9 = 7
48 ÷ 8 = 6
7 > 6
So, 63 ÷ 9 > 48 ÷ 8
Question 40.
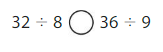
Answer: =
Explanation:
Divide the two numbers
32 ÷ 8 = 4
36 ÷ 9 = 4
4 = 4
So, 32 ÷ 8 = 36 ÷ 9
Question 41.
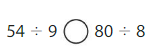
Answer: <
Explanation:
Divide the two numbers
54 ÷ 9 = 6
80 ÷ 8 = 10
6 < 10
So, 54 ÷ 9 < 80 ÷ 10
Question 42.
A crayon box has 48 crayons. There are 8 crayons in each row. How many rows of crayons are there?

Answer: 6
Explanation:
Given,
A crayon box has 48 crayons. There are 8 crayons in each row.
48/8 = 6
Thus there are 6 rows of crayons.
4.7 Divide with 0 or 1
Find the quotient
Question 43.
13 ÷ 13 = _____
Answer: 1
Explanation:
Divide the two numbers 13 and 13.
13/13 = 1
Thus the quotient is 1.
Question 44.
0 ÷ 9 = _____
Answer: 0
Explanation:
Divide the two numbers 0 and 9
Any number divided by 0 will be always 0.
0/9 = 0
Thus the quotient is 0.
Question 45.
3 ÷ 1 = _____
Answer: 3
Explanation:
Divide the two numbers 3 and 1.
3/1 = 3
Thus the quotient is 3.
Question 46.
Answer: 2
Explanation:
Divide the two numbers 1 and 2.
2/1 = 2
Thus the quotient is 2.
Question 47.
Answer: 0
Explanation:
Divide the two numbers 0 and 5.
Any number divided by 0 will be always 0.
Thus the quotient is 0.
Question 48.

Answer: 1
Explanation:
Divide the two numbers 10 and 10.
10/10 = 1
Thus the quotient is 1.
Question 49.
Number Sense
Which has the greatest quotient?
15 ÷ 15
0 ÷ 10
6 ÷ 1
8 ÷ 1
Answer: 8 ÷ 1
Explanation:
Check all the quotient
15 ÷ 15 = 1
0 ÷ 10 = 0
6 ÷ 1 = 6
8 ÷ 1 = 8
Thus the correct answer is option D.
4.8 Practice Division Strategies
Use any Strategy to find the quotient
Question 50.
16 ÷ 4 = _____
Answer: 4
Explanation:
Divide the two numbers 4 and 16.
16/4 = 4
Thus the quotient is 4.
Question 51.
72 ÷ 9 = ____
Answer: 8
Explanation:
Divide the two numbers 9 and 72.
72/9 = 8
Thus the quotient is 8.
Question 52.
20 ÷ 10 = _____
Answer: 2
Explanation:
Divide the two numbers 20 and 10.
20/10 = 2
Thus the quotient is 2.
Question 53.
Divide 18 by 6.
Answer: 3
Explanation:
Divide the two numbers 18 and 6.
18/6 = 3
Thus the quotient is 3.
Question 54.
Divide 49 by 7.
Answer: 7
Explanation:
Divide the two numbers 49 and 7.
49/7 = 7
Thus the quotient is 7.
Question 55.
Divide 30 by 6.
Answer: 5
Explanation:
Divide the two numbers 30 and 6.
30/6 = 5
Thus the quotient is 5.
4.9 Problem Solving: Division
Question 56.
Modeling Real Life
A group of 13 servicemen and 11 servicewomen are being honored at an event. They stand in 3 equal rows. How many servicemen and servicewomen are in each row?

Answer: 9
Explanation:
Given,
A group of 13 servicemen and 11 servicewomen are being honored at an event.
13 + 14 = 27
They stand in 3 equal rows.
27/3 = 9
Thus there are 9 servicemen and servicewomen in each row.
Division Facts and Strategies Cumulative Practice
Question 1.
Which expression is the same as 6 × 3?
A. 3 × 6
B. 3 + 3 + 3 + 3 + 3 + 3
C. 6 + 6 + 6
D. 6 × 6 × 6
Answer: A. 3 × 6
Explanation:
Given the expression 6 × 3
By using the multiplication equation
we can say that 3 × 6 is the same as 6 × 3
Thus the correct answer is option A.
Question 2.
Use the clues to find the number.
• The number is more than 10.
• The number is less than 20.
• When the number is divided by 3, the quotient is even.
• When the number is divided by 4, the quotient is odd.
What is the number?
A. 15
B. 12
C. 24
D. 16
Answer: B. 12
Explanation:
Let the number be 12
12 ÷ 3 = 4 (even)
12 ÷ 4 = 3 (odd)
Thus the correct answer is option B.
Question 3.
Which expression is equal to 6 × 7?
A. (7 × 8) – 2
B. (5 × 7) + (1 × 7)
C. (5 × 1) + (5 × 2)
D. (5 × 1) × 7
Answer: B. (5 × 7) + (1 × 7)
Explanation:
A. (7 × 8) – 2
56 – 2 = 54
B. (5 × 7) + (1 × 7)
35 + 7 = 42
C. (5 × 1) + (5 × 2)
5 + 10 = 15
D. (5 × 1) × 7
5 × 7 = 35
6 × 7 = 42
Thus the correct answer is option B.
Question 4.
Which number makes the statement true?
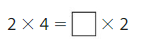
A. 4
B. 8
C. 16
D. 2
Answer: A. 4
Explanation:
2 × 4 = x × 2
8 = 2x
x = 8/2
x = 4
Thus the correct answer is option A.
Question 5.
Which equation is true?

Answer: C
Explanation:
A. (5 × 4) × 1 = (5 × 4) + 1
20 ≠ 21
B. (5 × 4) + 1 = (5 × 4) × 1
21 ≠ 20
C. (5 × 4) × 1 = (5 × 4) × 1
20 = 20
D. (5 × 4) × 1 = 5 + (4 × 1)
20 ≠ 9
Thus the correct answer is option C.
Question 6.
You earn 10 points for each level you complete in a video game. When you have to restart a level, you lose 2 points. You complete 9 levels but have to restart 6 levels. How many points do you have?

A. 78 points
B. 102 points
C. 90 points
D. 42 points
Answer: 78 points
Explanation:
Given,
You earn 10 points for each level you complete in a video game.
When you have to restart a level, you lose 2 points.
You complete 9 levels but have to restart 6 levels.
9 × 10 = 90 points
6 × 2 = 12 points
90 – 12 = 78 points
Thus the correct answer is option A.
Question 7.
The table shows the numbers of items at the finish line of a race.
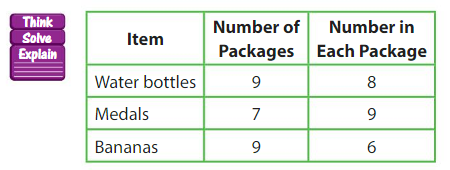
Part A How many medals are there?
Answer:
Medals:
Number of packages = 7
Number in each package = 9
7 × 9 = 63 medals
PartB Sixty students are running in the race. Is there enough of each item for all of the students? Explain.
Answer:
Given,
Sixty students are running in the race.
Water bottles:
Number of packages = 9
Number in each package = 8
9 × 8 = 72
Medals:
Number of packages = 7
Number in each package = 9
7 × 9 = 63 medals
Bananas:
Number of packages = 9
Number in each package = 6
9 × 6 = 54
Thus there are not enough bananas for all 60 students.
Question 8.
Which numbers are multiples of 2, 5, and 10?

Answer: 20
Explanation:
The fact family for 2, 5 and 10.
2 × 10 = 20
Thus the correct answer is option A.
Question 9.
Newton and Descartes share 18 toys equally. Which equation shows how many toys each has?
A. 18 ÷ 2 = 9
B. 18 – 2 = 16
C. 18 × 2 = 36
D. 18 ÷ 1 = 18
Answer: 18 ÷ 2 = 9
Explanation:
Given,
Newton and Descartes share 18 toys equally.
18/2 = 9
Thus the correct answer is option A.
Question 10.
Which multiplication fact can Newton use to check his answer?
72 ÷ 8 = 9

Answer: 9 × 8
Explanation:
72 ÷ 8 = 9
The multiplication fact for 9, 8 and 72 is
9 × 8 = 72
Thus the correct answer is option D.
Question 11.
Thirty dollars is divided evenly among 6 children. How much money (in dollars) does each child receive?

Answer:
Given,
Thirty dollars is divided evenly among 6 children
30/6 = 5
Thus each child receives 5 dollars.
Question 12.
Which expressions have a product of 16?

Answer: A. 4 × 4
Explanation:
The product of 16 is 4 × 4.
Thus the correct answer is option A.
Question 13.
Which equation shows the Multiplication Property of Zero?
A. 8 + 0 = 8
B. 8 – 0 = 8
C. 8 × 1 = 8
D. 8 × 0 = 0
Answer: D. 8 × 0 = 0
Explanation:
Any number multiplied by 0 is always 0.|
8 × 0 = 0
Thus the correct answer is option D.
Question 14.
One ticket to an amusement park costs $8. How much does it cost for a family of 4?


Answer: A. $32
Explanation:
Given,
One ticket to an amusement park costs $8.
8 × 4 = $32
Thus the correct answer is option A.
Question 15.
Which expression is represented by this number line?

A. 21 + 3
B. 3 × 7
C. 21 – 3
D. 7 + 3
Answer: B. 3 × 7
Explanation:
The count starts at 0.
It takes 3 jumps of 7.
3 × 7 = 21
Thus the correct answer is option B.
Question 16.
Which equations are in the fact family for 2, 10, and 20?

Answer: A, B, D, E
Explanation:
The fact family for 2, 10, 20 is:
2 × 10 = 20
10 × 2 = 20
20 ÷ 2 = 10
20 ÷ 10 = 2
Thus the correct answer is option A, B, D, E.
Division Facts and Strategies STEAM Performance Task

Dogs grow just like humans. They start as puppies, become adults, and then enter old age. But dogs age faster than humans. In general, to find the age of a small dog in dog years, multiply its age in human years by 5. To find the age of a large dog in dog years, multiply its age in human years by 7.
Question 1.
A small dog and a large dog are both 9 years old in human years. How old is each dog in dog years?
Answer:
Given,
A small dog and a large dog are both 9 years old in human years.
To find the age of a small dog in dog years, multiply its age in human years by 5.
5 × 9 = 45 years
Thus the age of a small dog is 45 years
To find the age of a large dog in dog years, multiply its age in human years by 7.
9 × 7 = 63 years
Thus the age of a large dog is 63 years.
Question 2.
The table shows the usual life spans of 6 dog breeds in dog years. Find each life span in human years. Organize the data in a bar graph.
Answer:
Question 3.
Write and answer a question about your graph.
Answer:
Draw the graph for the above table.
Question 4.
Cats also age faster than humans. The table shows the age of a cat for each human year.
a. A cat is 6 years old in human years. If the pattern in the table continues, how old is the cat in cat years?

Answer:
Given that,
A cat is 6 years old in human years.
By using the above table we can find the age of the cat in cat years.
6 years – 40 years
b. A cat is 10 years old in human years. How old is the cat in cat years?
Answer:
Given that,
A cat is 10 years old in human years.
By using the above table we can find the age of the cat in cat years.
1 year (human) = 4 years of cat
10 years = 56 years
Thus the age of cat in cat years is 56 years.
c. A small dog, a large dog, and a cat are each 6 years old (in human years). Order the animals by their ages (in animal years) from least to greatest.

Answer:
A small dog, a large dog, and a cat are each 6 years old (in human years).
Small dog in dog years, multiply its age in human years by 5.
6 × 5 = 30 years
To find the age of a large dog in dog years, multiply its age in human years by 7.
7 × 7 = 49 years
A cat is 6 years old in human years.
6 years – 40 years
Now arrange them from least to the greatest.
small dog, cat, and a large dog.
Question 5.
Use the Internet or another resource to answer each question.
a. What is another dog breed that is not listed in the table?
Answer: Bull Dog
b. About how long, how tall, and how heavy is one of these dogs?
Length: _____ inches
Height: _____ inches
Weight: ______ pounds
Answer:
The length, height, and weight of the bulldog is given below
length – 12 to 15 inches
height – 12 to 15 inches
weight – 40 to 43 pounds
c. What is one interesting fact about this dog breed?
Answer:
The interesting fact about bulldog is
1. These are independent
2. The dogs were bred for their wrinkles.
d. About how long would you expect this breed to live?
Answer: The life span of the bulldog is 8 to 10 years.
Conclusion:
I hope that the Big Ideas Math Answers Grade 3 Chapter 4 Division Facts and Strategies Solution Key is useful for the students who are preparing for the exams. You can get the free download link of Big Ideas Math Book Grade 3 Chapter 4 Division Facts and Strategies Answer Key PDF. Stay in touch with us to find the solutions for other chapters of 3rd grade.